求解柔性作业车间调度的遗传算法综述
黄学文,陈绍芬,周阗玉,孙宇婷
(大连理工大学 经济管理学院,辽宁 大连 116024)
0 引言
调度通过合理安排生产资源,以缩短生产时间和提高资源利用率为目的,在生产系统中扮演着重要的角色。作业车间调度问题(Job-shop Scheduling Problem, JSP)是一类经典的调度问题,其通过安排n个工件在m台机器上的加工顺序来优化一个或多个调度指标。在JSP中,每个工件由一道或多道具有固定加工顺序的工序构成,且每道工序的加工机器唯一。柔性作业车间调度问题(Flexible Job-shop Scheduling Problem, FJSP)是JSP的扩展,它允许一道工序有多台可供选择的加工机器,且在不同机器上的加工时间可能存在差异,即相对于JSP,FJSP具有一般性,更符合柔性制造系统的实际情况。在FJSP中,机器柔性虽然能够提高制造系统的执行效率,但是扩大了可行解的范围,增加了求解问题的难度和复杂性。
FJSP是一类复杂的NP-hard问题[1],元启发式算法为求解该问题的重要方法,如遗传算法(Genetic Algorithm, GA)[2-6]、禁忌搜索(Tabu Search, TS)算法[7-9]、蚁群优化(Ant Colony Optimization, ACO)算法[10-11]和粒子群优化(Particle Swarm Optimization, PSO)算法[12-13]等,其中遗传算法因操作简单、通用性强,且具有良好的鲁棒性,而成为求解FJSP最受欢迎的算法之一[14-15]。
遗传算法由Holland于20世纪60年代提出[16]。首先,遗传算法将待求解问题的解通过染色体编码方法映射为编码空间中的染色体(chromosome),染色体由一定数量的基因构成,基因及其在染色体上的排列决定了染色体的语义特征;其次,遗传算法是一种基于群体的方法,染色体代表群体中的个体,通过对群体进行迭代遗传操作(包括选择、交叉、变异等)得到问题的最优解或近似最优解。其中,染色体编码方法和遗传算子(特别是交叉算子和变异算子)设计是构造遗传算法首先需要考虑的两个重要且互相交织的问题,二者对求解效率和质量的影响非常明显[17-18],即对于不同优化问题,需要设计满足问题特定约束条件的染色体编码方法,同时交叉和变异算子的设计或选择又需要遵守所采用的染色体编码方法的语义特征。需要说明的是,选择算子的选择和设计一般独立于具体的染色体编码方法,在求解各类问题中具有高度的通用性,常用的有轮盘赌、锦标赛和精英保留等选择算子,具体参见文献[19- 20]。
遗传算法应用于FJSP时遵循遗传算法求解一般问题的标准流程,即设计染色体编码方法来表达FJSP,并形成初始种群,然后对群体进行迭代遗传操作。具体表现为:利用选择算子根据个体的适应度进行选择操作,利用交叉和变异算子对染色体进行交叉和变异操作,完成种群的不断繁殖和迭代进化;满足迭代的终止条件后,输出搜索到的最优解或近似最优解。自PAREDIS[21]第一次采用遗传算法求解FJSP以来,在过去的30年中,学者们设计了许多形式各异的遗传算法,以及相应的染色体编码方法和遗传算子,并取得了良好的结果。本文对求解FJSP的遗传算法中的两个关键内容——染色体编码方法以及交叉和变异算子进行综述,以为进一步开展遗传算法求解FJSP提供系统性的理论支持。
1 FJSP描述
FJSP可描述为:有n个相互独立的待加工工件(记为工件集J={J1,…,Jn})在m台加工机器(记为机器集M={M1,…,Mm})上加工,每个工件Ji包含ni道具有固定加工顺序的工序,即Ji={Oi1,Oi2,…,Oini},且工序Oij可在其候选机器集合Mij(Mij⊆M)中的任意一台机器上加工。FJSP需要确定每道工序的加工机器(路径子问题),并确定所有工序在机器上的加工顺序(调度子问题),以实现对一个或多个调度目标的优化,如最大完工时间、总机器负荷、总延迟时间、最大松弛时间等。
求解FJSP通常需要满足如下假设条件:
(1)0时刻,所有工件均处于待加工状态,所有机器均处于空闲状态。
(2)同一时刻,同一台机器只能加工一个工件的某道工序。
(3)同一时刻,同一工件只能被一台机器加工,且不允许中断正在加工的工序。
(4)同一工件的工序加工顺序固定且不可更改,不同工件的工序间没有顺序约束关系。
基于上述FJSP的描述,很多学者提出求解FJSP的0-1整数规划模型[22-25],另外析取图模型也常用于描述FJSP[26-28],本文不再给出这些模型的数学定义。
根据生产系统的柔性程度,FJSP可分为完全柔性作业车间调度问题(Total FJSP, T-FJSP)和部分柔性作业车间调度问题(Partial FJSP, P-FJSP)两类。在T-FJSP中,对于任意工序Oij,可选择机器集合M中的任意一台机器加工,即Mij=M;在P-FJSP中,至少存在一道工序Oij,有Mij⊂M且Mij≠M。表1所示为3个工件在3台机器上加工的P-FJSP实例,其中“-”表示该工序无法在对应机器上加工。
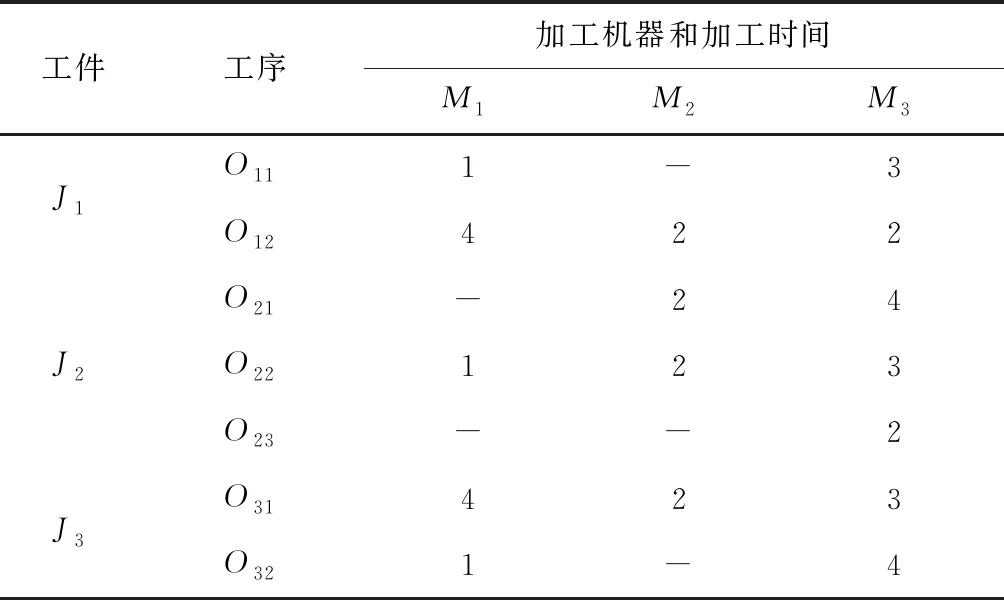
表1 3×3的P-FJSP实例
2 染色体编码方法
染色体编码方法是遗传算法首要解决的问题[18],原因是:①它定义了染色体上的基因排列形式及其语义特征,从而决定了编码空间基因型与解空间表现型之间的映射关系和遗传搜索空间的大小;②它严重影响交叉和变异算子的设计、选择和执行[17-18]。一个不完善的染色体编码方法甚至会在交叉或变异操作之后产生不可行解,此时需要设计额外的染色体修复机制来保证解的可行性,不仅降低了遗传算法的计算效率,还增加了设计的复杂性。
本文将求解FJSP的染色体编码方法分为5大类,即MSOS(machine selection and operation sequence)编码、三元组编码、表格编码、矩阵编码和A/B串编码。除此之外,还有一些不常使用的染色体编码方法,如TAY等[29]提出的三段编码。
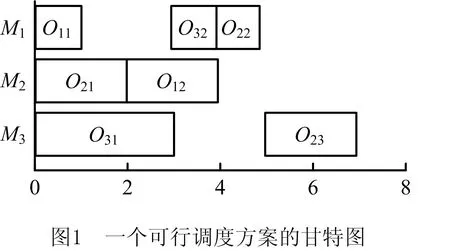
设表1所示FJSP的一种工序加工顺序为(O21,M2)≻(O11,M1)≻(O31,M3)≻(O12,M2)≻(O32,M1)≻(O22,M1)≻(O23,M3),其中:二元组(Oij,Mk)表示Oij在机器Mk上加工;符号“≻”表示工序之间的加工顺序性;工序O21在该加工顺序中为第一个被调度的工序。图1所示为该工序的加工顺序在半主动调度(1)调度分为4种类型,即半主动调度、主动调度、非延迟调度和混合调度,其中半主动调度是在不改变任意机器上工序加工顺序的前提下,没有任何工序可以减小加工开始时间的调度。其他几种调度类型可参见文献[30]。下的甘特图。为了便于说明问题,以下分别用这5类编码方法表示图1对应的调度方案。
2.1 MSOS编码
在求解FJSP的各类遗传算法中,MSOS编码方法应用得最广泛,其最初由HO等[31]提出。MSOS编码将染色体分为机器选择串(machine selection)和工序顺序串(operation sequence)两条子串(或子染色体),分别用于解决路径子问题和调度子问题。
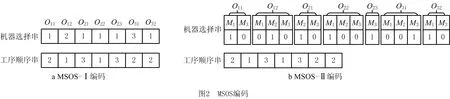
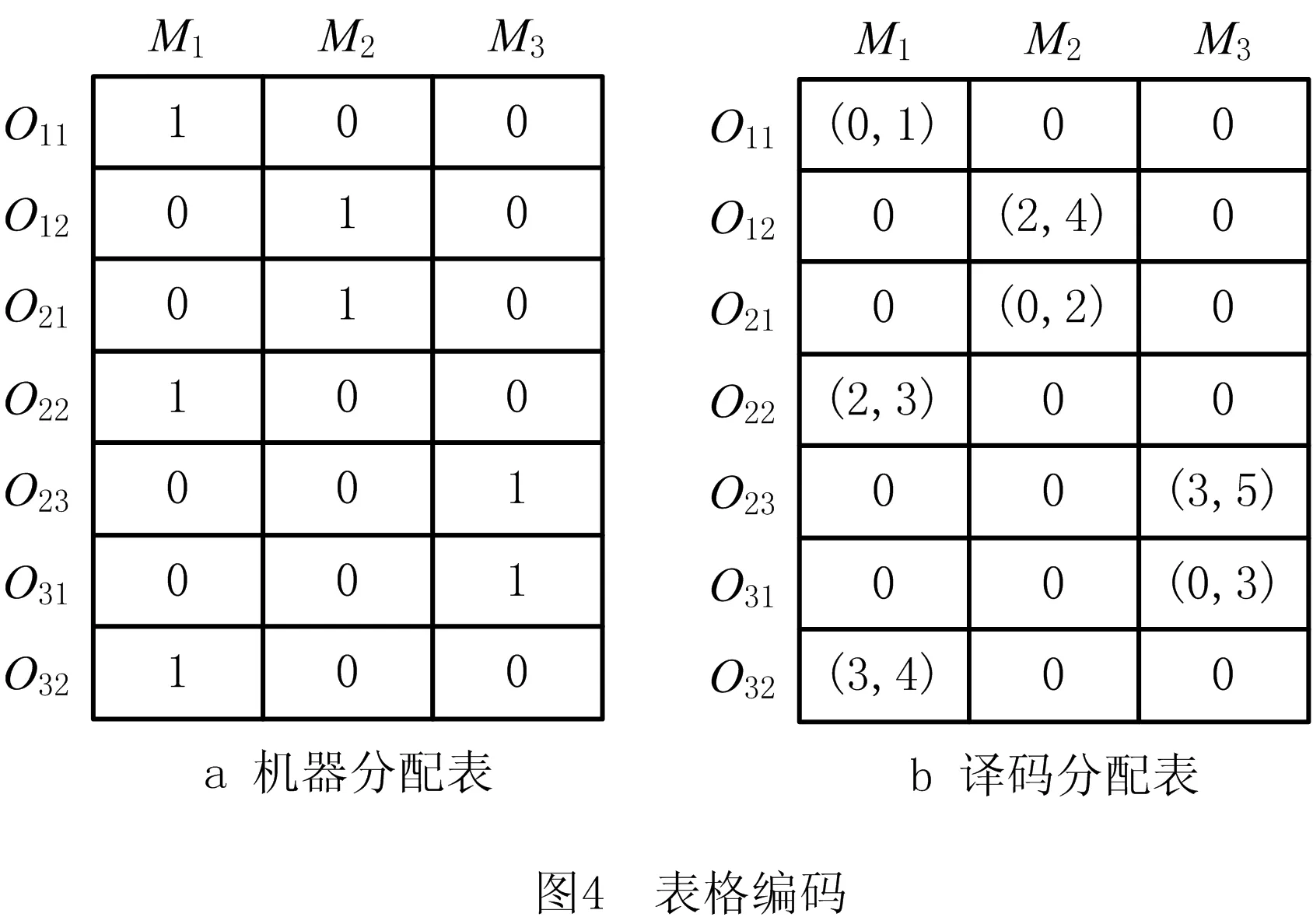
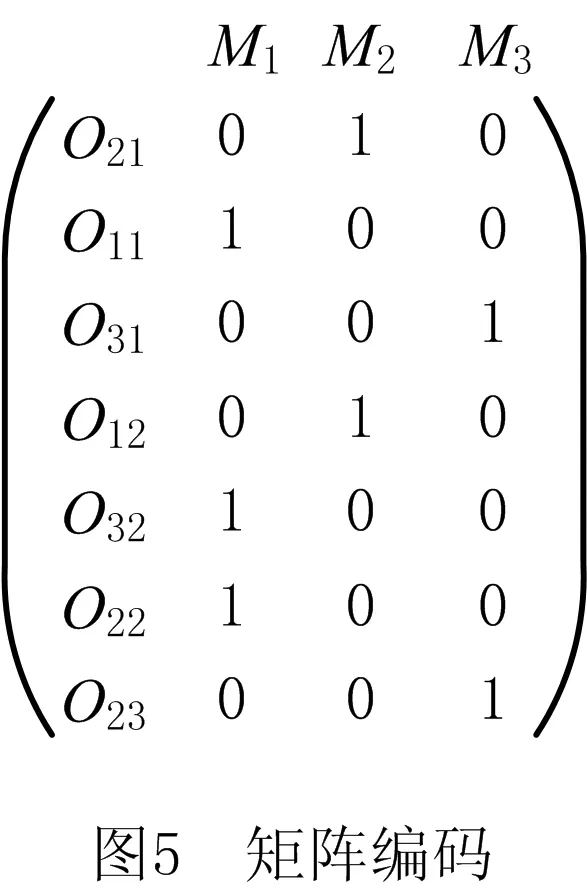
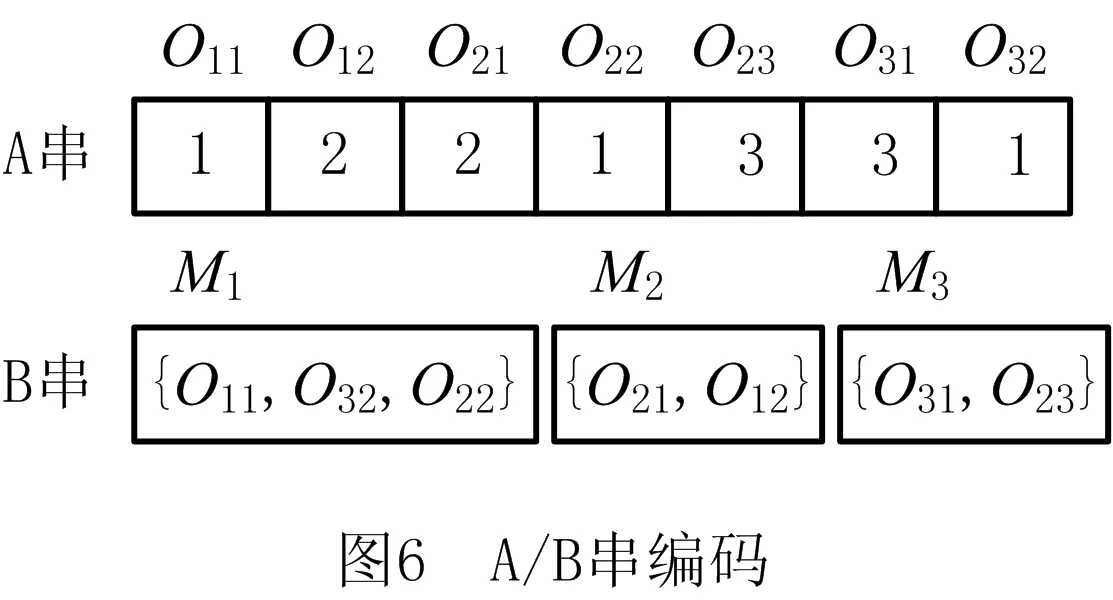
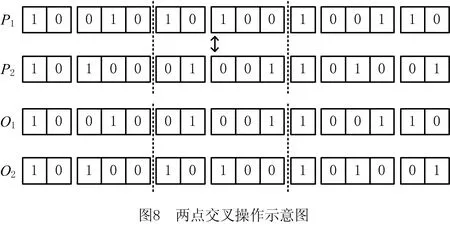
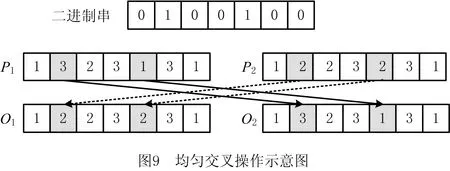
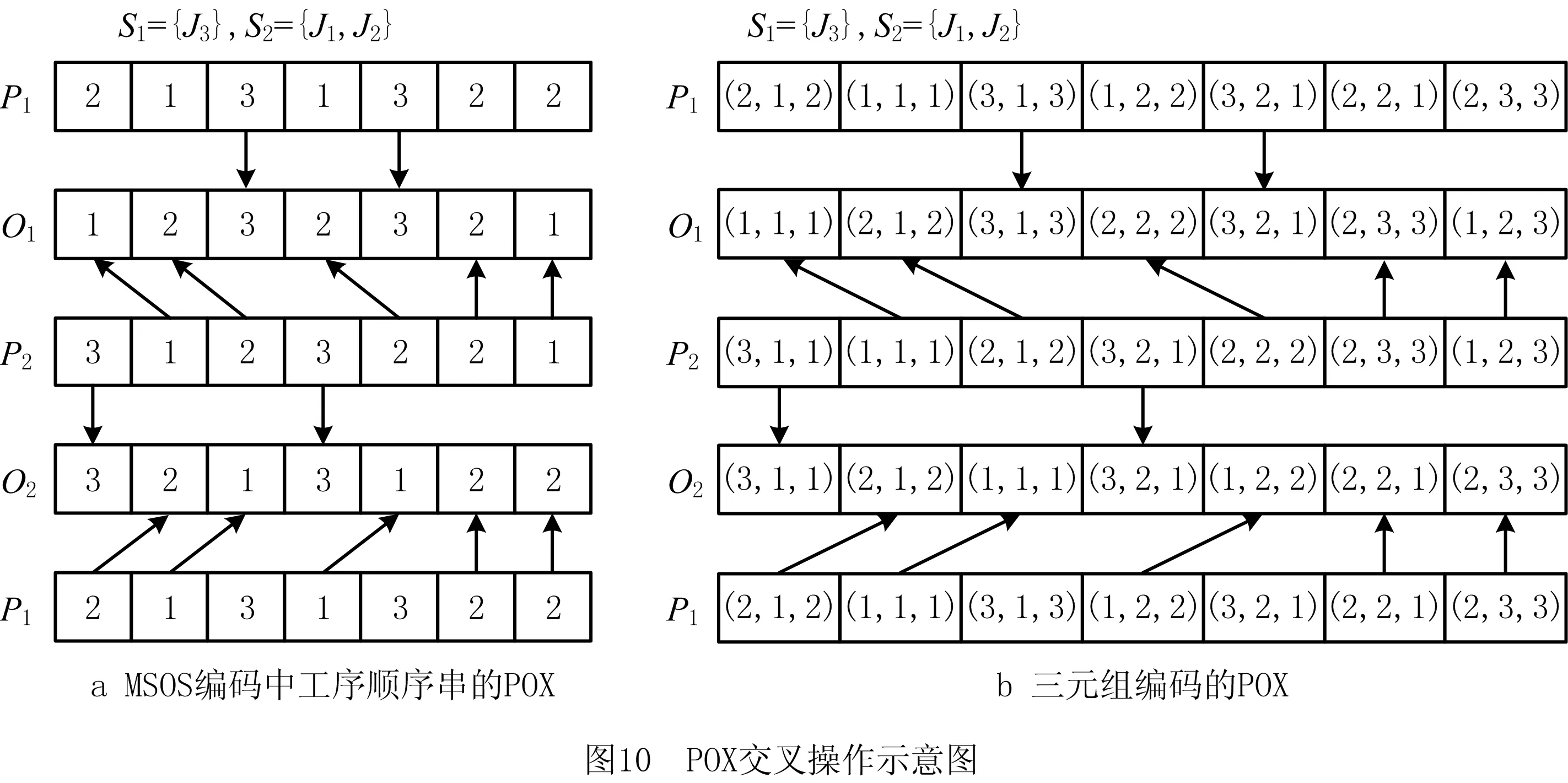
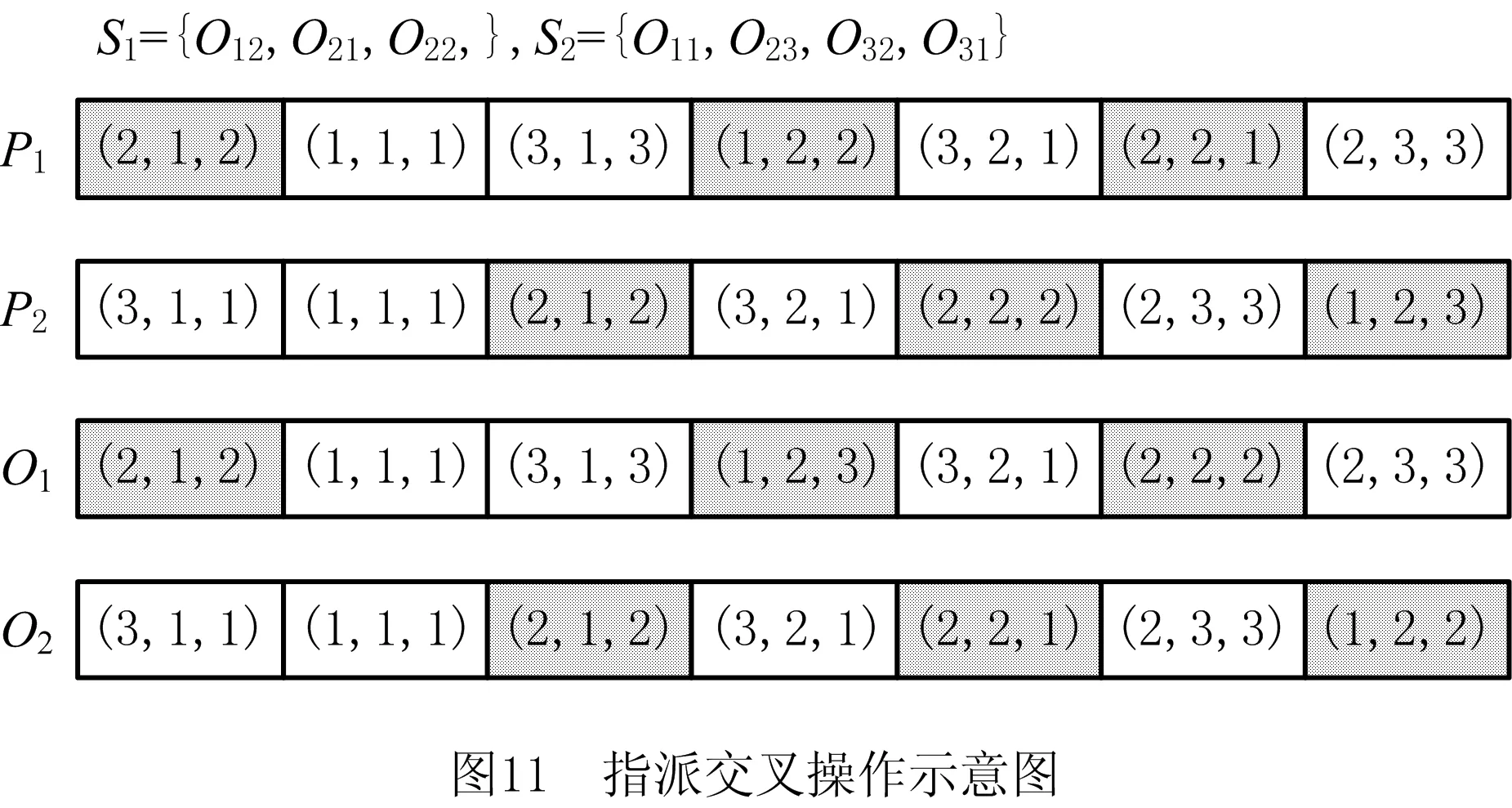
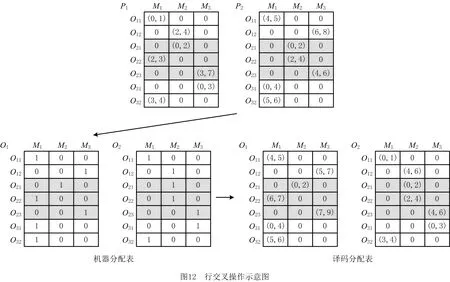
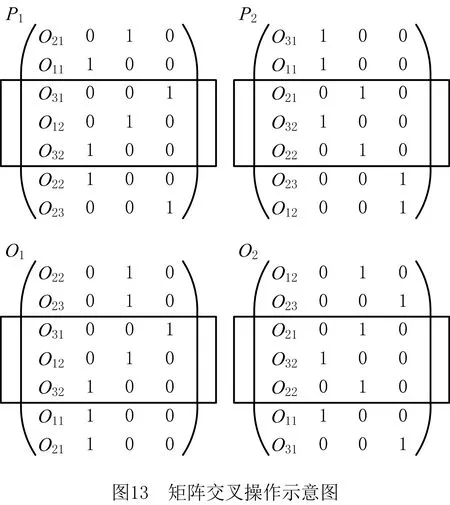
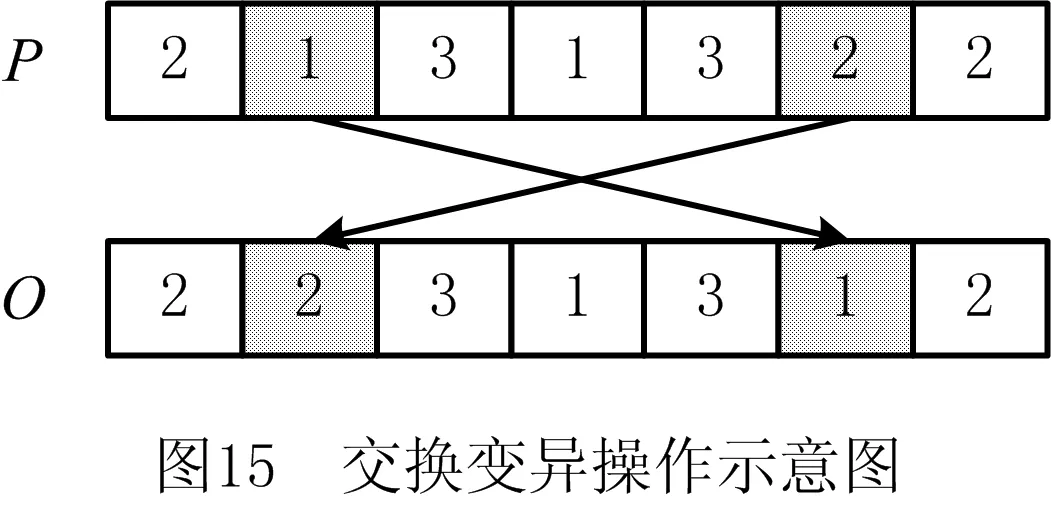
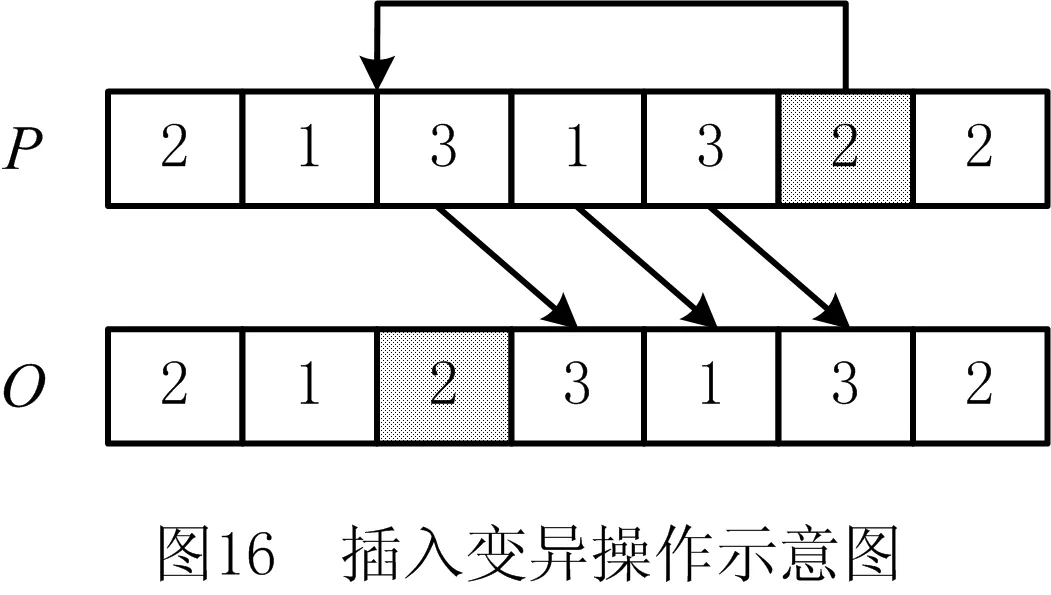
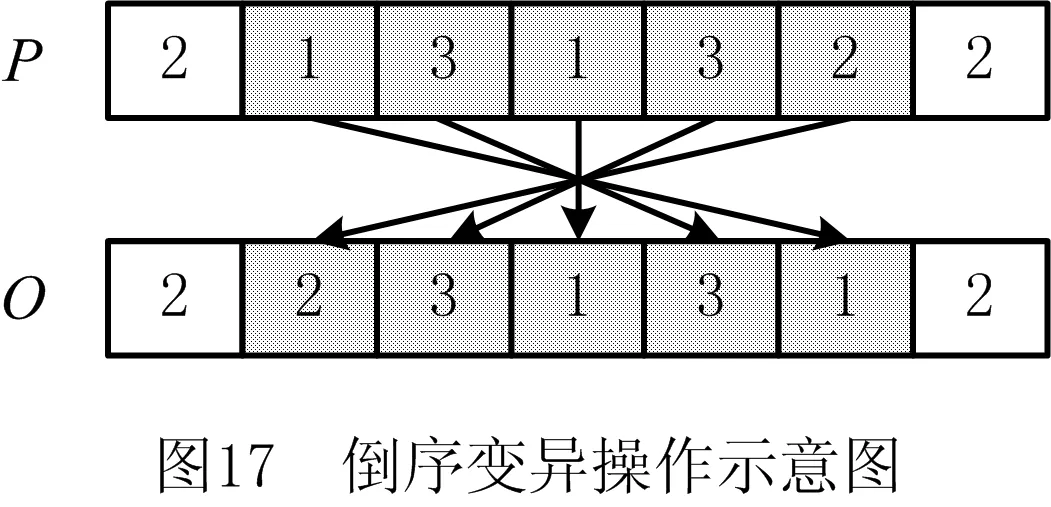
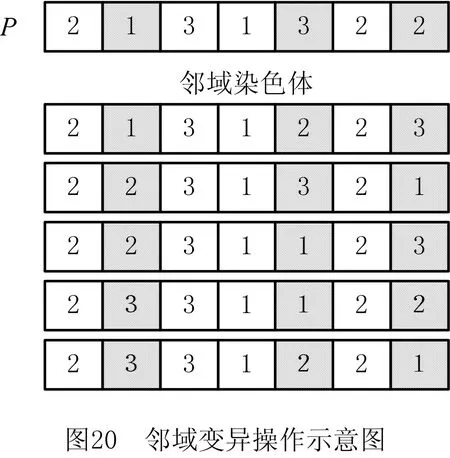
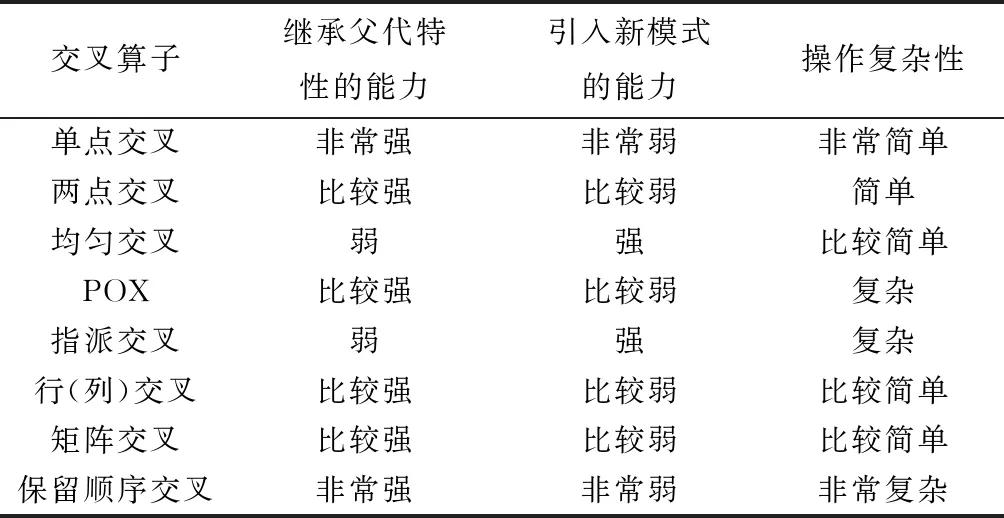
i=k,j=x-lk-1,lk-1 机器选择串中的基因编码又分为两种方法:①将机器选择串上的基因用该位置对应工序的加工机器的机器号或机器索引号(所选加工机器在候选机器集合中的索引)编码[2, 8, 32-40];②将机器选择串上的基因用一个0-1数组编码[31, 41-42],其中0-1数组的长度等于该基因对应工序的候选机器集合的模,且每个0-1数组中有且只有一个元素的值为1,其他值均为0,机器选择串中每个位置上的0-1数组表示对应工序由1所对应的机器加工。 根据前文机器选择串的编码方法,将MSOS编码分为MSOS-I编码和MSOS-II编码,分别对应机器选择串中编码的方法①和方法②。图2所示为MSOS-I和MSOS-II编码方法对图1调度方案的编码示例,两种编码方法中的工序顺序串完全一致,例如该串中的两个“1”从左到右依次表示工件J1的第1道和第2道工序,即工序O11和O12,第1个基因值“1”(位于串中第2位)表示工序O11,为全部工序中第2个被调度的工序。另一方面,两种编码方法中的机器选择串各不相同,其中图2a的机器选择串是MSOS-I(采用机器索引号编码)的编码结果,图2b的机器选择串是MSOS-II的编码结果。例如,图1中工序O11选用机器M1加工,MSOS-I编码通过设置机器选择串中第1个基因座的基因为“1”来表示工序O11选用了其候选机器集合{M1,M3}中的第1台机器M1加工;MSOS-II编码通过将0-1数组中的机器M1对应位置的值设为“1”来表示O11选用机器M1加工。 显然,任意一个由MSOS编码生成的染色体总可以解码成一个可行的调度方案,这是因为机器选择串总为每道工序指派一台可行的加工机器,且工序顺序串总可以解码为一个可行的调度方案(基于工序的编码总对应JSP的一个可行调度[18],当每道工序指派了一台加工机器后,FJSP变成一个标准的FJSP)。另外,MSOS编码中的两条子串分别有不同的语义特征,且在编码阶段采用相互独立的编码方法,因此可以使用符合各自语义特征的交叉算子和变异算子分别对两条子串进行遗传操作。 三元组编码方法生成的任意一条染色体总可以解码成一个可行的调度方案。三元组(i,j,k)中的3个变量有不同的语义特征,其中前两个变量(即i,j)及其从左到右的排列顺序表示调度子问题,第3个变量(即k)表示路径子问题,因此可以结合FJSP中的两个子问题的定义以及这些变量的具体语义特征进行单独的交叉和变异操作。 表格编码最初由MESGHOUNI[49]提出,其首先通过随机算法或启发式算法等分配算法为每道工序指派一台加工机器,得到一个机器分配表,再运用调度规则将机器分配表转换为确定了工序的加工开始时间、加工完成时间或加工机器的译码分配表,得到一个完整的调度方案。在译码分配表时,调度规则用于解决调度过程中出现多道工序,需要在同一时间段使用同一台机器的冲突,即保证每次只有一个工序被调度。常用的调度规则有最短加工时间优先(Shortest Processing Time first,SPT)、最长加工时间优先(Largest Processing Time first,LPT)和后进先出(Last In First Out,LIFO)等。 表格编码共有3种形式,分别是工序机器编码(Operations Machines Coding, OMC)、平行工件编码(Parallel Jobs Representation,PJsR)和平行机器编码(Parallel Machine Representation, PMR)。下面以OMC为例对表格编码法进行说明。 首先,通过一种分配算法,如theapproach by localization[50],为每道工序确定一台加工机器,得到一个机器分配表,如图4a所示。机器分配表中的行表示工序,列表示机器;单元格中的值为1表示该工序选择了对应列上的机器,值为0表示未选择对应列上的机器。显然,机器分配表中任意一行有且只有一个单元格的值为1(因为每道工序只能选择一台机器)。然后,通过调度规则将机器分配表中的数值1转换为该工序的加工开始时间和加工完成时间,从而得到译码分配表,即一个可行的调度方案,如图4b所示。译码分配表中第1行第1列的二元组为(0,1),表示工序O11在机器M1上的加工开始时间为0,加工完成时间为1。 这种编码方法生成的任意一条染色体总表示一个可行调度方案,然而因为基于调度规则生成的调度方案不能保证是全局最优解或近似最优解,所以采用表格编码的遗传算法不能保证生成高质量的调度方案。 这种编码方法可看作为三元组编码的变型,只是将三元组编码中选择的机器从机器号表示换成0-1数组表示,因此矩阵编码继承了三元组编码的特点。 CHEN等[53]提出A/B串编码,其将一条染色体分成A,B两条子串,其中:A串与MSOS-I编码中的机器选择串相同(此处采用机器号编码),用于确定每道工序的加工机器;在A串已经确定每台机器加工工序的基础上,B串用于记录每台机器上的工序加工顺序,因此B串共有m个基因。图1中的调度方案采用该编码方法的结果如图6所示,由A串可得,机器M1需要加工工序O11,O22,O32,M2需要加工工序O12,O21,M3需要加工工序O23,O31。B串基于A串给出了各台机器上的工序加工顺序,即O11≻O32≻O22,O21≻O12和O31≻O23。 A/B串编码无法保证任意一条染色体均可解码为一个可行的调度方案,因此需要额外的染色体修复机制。这是因为:①B串中各机器上的加工工序不一定与A串确定的在同一台机器上的加工工序一致,特别是在交叉和变异操作之后;②B串只确定了每台机器上的工序加工顺序,全部工序的加工顺序可能产生循环调度现象,即死锁状态。例如,若将图6中B串机器M3上工序的加工顺序改为O23≻O31,则会出现循环调度O32≻O22≻O23≻O31≻O32。以上情况表明,B串依赖A串,且B串的遗传操作要遵循多重约束(即解决上述两个问题),从而极大增加了B串交叉和变异的复杂性。 遗传算法主要有选择、交叉和变异3类遗传算子,其中交叉和变异算子直接以染色体为操作对象,与染色体的编码方法及其所表示的语义特征密切相关。 交叉算子是遗传算法产生新个体的主要操作,其在很大程度上决定算法性能的高低[54]。交叉操作前先需要选择性地对群体中的个体进行两两配对,然后再以某种方式交换配对染色体的部分基因,形成两条新染色体(即子代染色体)。目前,在求解FJSP的遗传算法中使用的交叉算子主要有以下8种形式。 3.1.1 单点交叉 单点交叉为经典的交叉算子[53, 55],即在染色体中随机选择一个交叉点,并互换两条染色体交叉点之后的所有基因,产生两条新的染色体,具体操作过程如下: 步骤1随机选择两条染色体P1和P2,并随机设置某个基因座为交叉点。 步骤2相互交换交叉点之后的所有基因,产生两条新的染色体O1和O2。 单点交叉适用于MSOS中的机器选择串和A/B串编码中的A串,图7所示为MSOS-I编码中的机器选择串应用单点交叉的一个实例,图中纵向虚线表示交叉点。然而,单点交叉不适用于其他子串或编码方法。以MSOS的工序顺序串为例,若采用单点交叉算子,则子代染色体不能保证工件号i有且仅出现ni次,即不能保证解的可行性。 3.1.2 两点交叉 两点交叉为经典的交叉算子[56-57],即在染色体中随机选择两个交叉点,并互换两个交叉点之间的所有基因,产生两条新的染色体,具体操作过程如下: 步骤1随机选择两条染色体P1和P2,并随机设置两个基因座为交叉点。 步骤2相互交换两个交叉点之间的所有基因,产生两条新的染色体O1和O2。 显然,两点交叉适用于MSOS的机器选择串和A/B串编码的A串,但不适用于其他子串或编码方法,原因与单点交叉算子相同。图8所示为MSOS-II编码中的机器选择串(用0-1数组表示基因)应用两点交叉的一个实例。 3.1.3 均匀交叉 均匀交叉为经典的交叉算子[58-61],属于多点交叉,其通过随机产生的一条与染色体长度相同的二进制串,来决定子代染色体上基因与父代染色体上基因之间的继承关系,具体操作过程如下: 步骤1随机选择两条染色体P1和P2,并初始化两条空的子代染色体O1和O2。 步骤2随机产生一条与染色体长度相同的二进制串w1,w2,…,wi,…,wl,其中l表示染色体的长度。 步骤3若wi=0,则O1第i个基因座上的基因继承P1相同基因座上的基因,O2第i个基因座上的基因继承P2相同基因座上的基因;若wi=1,则O1第i个基因座上的基因继承P2相同基因座上的基因,O2第i个基因座上的基因继承P1相同基因座上的基因。 均匀交叉适用于MSOS的机器选择串和A/B串编码的A串,但不适用于其他子串或编码方法,原因与单点交叉算子相同。图9所示为MSOS-I编码中的机器选择串应用均匀交叉的一个实例。 3.1.4 POX POX(precedence preserving order-based crossover)是典型适用于基于工序编码的交叉算子[62-63],该算子可以保证所有工件在父代和子代中出现的次数相同,并保持任意工件工序之间的顺序约束关系,具体操作过程如下: 步骤1随机选择两条染色体P1和P2,并初始化两条空的子代染色体O1和O2。 步骤2将工件集随机分为两个非空的集合S1和S2,且S1∪S2=J,S1∩S2=∅。 步骤3将P1中属于集合S1的工件所对应的基因复制到O1相同的基因座上,再将P2中删除了O1中已确定的基因后剩余的基因从左到右依次填充到O1的空位上。 步骤4互换P1和P2的角色,生成O2。 图10a所示为MSOS中的工序顺序串应用POX的示例;另外,POX也可用于三元组编码和矩阵编码,对于这两种编码,POX算子仅作用于工序加工顺序的相关变量上,不改变工序的加工机器。图10b所示为三元组编码应用POX的示例,其中所有工序的加工机器不发生改变。 需要说明的是,与POX相似的交叉算子还包括基于工件的交叉(Job-Based Crossover, JBX)算子、部分映射交叉(Partial-Mapped Crossover,PMX)算子、顺序交叉(Order Crossover,OX)算子和线性顺序交叉(Linear Order Crossover, LOX)算子等,具体参见文献[2, 17, 64]。 3.1.5 指派交叉 指派交叉专用于三元组编码方法[65],属于均匀交叉的变型。该交叉算子仅对三元组(i,j,k)中的变量k进行操作,以改变部分工序的加工机器,具体操作过程如下: 步骤1随机选择两条染色体P1和P2,并初始化两条空的子代染色体O1和O2。 步骤2将P1中所有三元组(i,j,k)中的变量i和j复制到O1相应的位置。 步骤4互换P1和P2的角色,生成O2。 图11所示为三元组编码应用指派交叉的一个实例。 3.1.6 行(列)交叉 行(列)交叉专用于表格编码方法,是两点交叉的变型[66]。因为行(列)交叉只涉及染色体上相同基因座上的基因交换,所以产生的子代染色体均可解码成可行的调度方案。行(列)交叉的具体操作过程如下: 步骤1随机选择两条染色体P1和P2,并初始化两条空的子代染色体O1和O2。 步骤2随机选择一个工件Ji(1≤i≤n),O1中所有属于工件Ji的工序都选择与P1相同的机器,剩余工序都选择与P2相同的机器(随机选择每个工件中的第j道工序,O1中所有工件的第j道工序都选择与P1相同的机器,剩余的工序都选择与P2相同的机器)。 步骤3根据得到的O1的机器分配表,计算每道工序的加工开始和加工结束时间,得到O1的译码分配表。 步骤4互换P1和P2的角色,生成O2。 图12所示为OMC应用行交叉的一个实例,本例中随机选择工件J2作为被选中的工件,交叉操作后形成两个新的机器分配表,又利用调度规则重新得到每道工序的加工开始和加工完成时间。需要说明的是,行(列)交叉算子的设计与具体的表格编码方法密切相关,关于PJsR和PMR的行(列)交叉算子,请参见文献[49]。 3.1.7 矩阵交叉 矩阵交叉是为矩阵编码专门设计的交叉算子,属于两点交叉的变型[51],具体操作过程如下: 步骤1随机选择两条染色体P1和P2,并初始化两条空的子代染色体O1和O2。 步骤4互换P1和P2的角色,生成O2。 图13所示为矩阵交叉操作的一个实例,本例中h1=3,h2=5。显然,这种交叉操作后的子代染色体很可能不能遵守同一工件中工序之间的顺序约束关系,从而生成不可行的调度方案,例如图13中的子代染色体O1中的工序O22排在工序O21之前。 3.1.8 保留顺序交叉 保留顺序交叉是为A/B串编码中的B串专门设计的交叉算子[53],该算子只对某台机器上的工序加工顺序进行操作,具体操作过程如下: 步骤1随机选择两条染色体P1和P2,并初始化两条空的子代染色体O1和O2。 步骤2随机选择染色体的某个基因座(设为第k个基因座,即第k台机器),l=min {l1,l2},其中l1和l2分别为P1和P2染色体在第k台机器上加工的工序数量;当l≥2时,从[1,l]之间产生两个随机数x1和x2(1≤x1 步骤3将P1的第k个基因座之外的所有基因复制到O1的相应位置。 步骤4互换P1和P2的角色,生成O2。 图14所示为A/B串编码中的B串应用保留顺序交叉的一个实例,本例随机选择染色体第1个基因M1上第1个位置到第2个位置上的工序进行工序加工顺序重排,因为P1中只有工序O32出现在P2的M1上,所以O1第1个基因的工序加工顺序不变;而P2中M1上的工序加工顺序为O22≻O32,根据P1中M1上的工序顺序,M1上的工序加工顺序在O2中发生逆转,即O32≻O22。 变异算子是遗传算法产生新个体的另一种重要操作,其通过将染色体中某些位置上的基因用其他等位基因替换来产生新个体。变异操作可显著改善算法的局部搜索能力,并通过防止有效基因遗失来维持群体的多样性,有助于避免遗传算法早熟。目前,在求解FJSP的遗传算法中使用的变异算子主要有6种形式。 3.2.1 交换变异 交换变异通过交换染色体两个不同基因座上的基因来产生新的染色体[17, 59],具体操作过程如下: 步骤1随机选择一条染色体P。 步骤2随机选择染色体P上的两个基因座,交换两个基因座上的基因,生成子代染色体O。 图15所示为MSOS-I编码中的工序顺序串应用交换变异的一个实例。需要说明的是,交换变异只适用于MSOS的工序顺序串,不适用于其他子串或编码方法。因为其他子串或编码方法的染色体上各个基因座的等位基因不同,交换不同基因座上的基因可能使子代染色体无法解码成可行的调度方案。 3.2.2 插入变异 插入变异通过将某基因座上的基因插入染色体的其他基因座上来产生新的染色体[28, 61, 67],具体操作过程如下: 步骤1随机选择一条染色体P。 步骤2随机选择染色体P上的一个基因,将该基因随机移动到染色体的其他基因座上,生成子代染色体O。 插入变异只适用于MSOS的工序顺序串,原因与交换变异相同。图16所示为MSOS-I编码中的工序顺序串应用插入变异的一个实例。 3.2.3 倒序变异 倒序变异通过逆转染色体中任意两个基因座之间的基因排列顺序来产生新的染色体[17],具体操作过程如下: 步骤1随机选择一条染色体P。 步骤2随机选择染色体P上的两个基因座,逆转两个基因座之间基因的排列顺序,生成子代染色体O。 倒序变异只适用于MSOS的工序顺序串,原因与交换变异相同。图17所示为MSOS-I编码中的工序顺序串应用倒序变异的一个实例。需要说明的是,相比交换变异和插入变异,倒序变异对染色体产生的改变更大。 3.2.4 智能变异 智能变异主要用于路径子问题的变异操作[45, 60],一般基于减少某道工序的加工时间或平衡不同机器间的机器负荷(即机器全部加工工序的加工时间之和)进行操作。以下以减少某道工序的加工时间为例,说明其具体操作过程: 步骤1随机选择一条染色体P,然后从在机器负荷最大的机器上加工的工序中随机选择一道工序Oij。 步骤2从工序Oij的候选机器集合中选择加工时间最少的机器Mk,将机器Mk分配给工序Oij。 图18所示为三元组编码应用智能变异的一个实例,本例中机器M3的负荷最大(M1的负荷为3,M2的负荷为4,M3的负荷为5,如图1),若随机选择的工序是O31,则变异操作之前,该工序的加工机器和加工时间分别为机器M3和3;变异操作之后,将工序O31重新分配给加工时间最少的机器,即机器M2,则相应的加工时间减少到2。显然,智能变异适用于FJSP的所有染色体编码方法。 3.2.5 PPS变异 PPS(precedence preserving shift mutation)变异是插入变异的变型[46, 65],其通过随机选择一个工序,在保持任意工件的工序之间顺序约束关系的前提下,改变全部工序的加工顺序,具体操作过程如下: 步骤2将工序Oij随机移动到任意一个x1到x2之间的位置上,形成子代染色体O。 图19所示为三元组编码应用PPS变异的一个实例,本例被选中的工序O31是工件J3中的第1道工序,其可以移动到工序O32之前的任意一个基因座上,即有4个可以移动的位置。最终将工序O31移动到第1个基因座上,产生子代染色体O。显然,PPS变异适用于三元组编码、矩阵编码和MSOS中的工序顺序串。 3.2.6 邻域变异 邻域变异专用于MSOS的工序顺序串[2, 17, 68],通过对一条被选定的染色体进行邻域变换(即对染色体产生小的扰动或变化)生成该染色体的多个邻域染色体,从中随机选择一条作为子代染色体(也可以从邻域染色体中选择最好的一个作为子代染色体,但该方法计算成本过高),具体操作过程如下: 步骤1随机选择一条染色体P,再随机在染色体P上选择x个基因座(一般1 步骤2通过改变x个基因座上的基因排列顺序,生成染色体P所有的邻域染色体。 步骤3从生成的邻域染色体中随机选择一条作为子代O。 图20所示为MSOS中的工序顺序串应用邻域变异的一个实例,本例选择3个基因座的基因,通过改变3个基因值的排列顺序可以得到5个邻域染色体。 基于前文可以看出,染色体编码方法设计是应用遗传算法求解FJSP的关键,同时染色体编码方法又对交叉、变异算子的选择或设计有重要影响,并最终对遗传算法求解FJSP的效率和质量产生根本影响,即染色体编码方法与交叉、变异算子之间相互交织、互相影响。为此,本文首先评价前文所述的交叉和变异算子,然后对各类染色体编码方法进行整体评价。 交叉算子的设计决定了子代与父代之间的继承关系和交叉算子操作(或计算)的复杂性。就子代与父代之间的继承关系而言,文献[17,69]指出,交叉算子设计需要考虑子代继承父代特性的能力和子代引入新模式的能力,其中子代继承父代特性的能力表示交叉操作应尽可能减小对父代的改变,即尽可能地继承父代的特性,这有利于遗传算法快速收敛,单点交叉、两点交叉及两者的变型交叉算子均具有较强的子代继承父代特性的能力;子代引入新模式的能力表示交叉操作应尽可能增大对父代的改变,从而扩大遗传算法的搜索能力,均匀交叉及其变型交叉算子均具有较强的引入新模式的能力。就交叉算子的操作复杂性而言,交叉算子设计越简单,交叉操作的复杂性越低,算法的整体计算效率越高。一般经典交叉算子的操作复杂性较低,而针对某种特定编码方法设计的交叉算子的操作复杂性较高。在前文所述的8类交叉算子中,除单点交叉、两点交叉和均匀交叉为经典交叉算子外,其他都是为适应FJSP及其特殊编码方法设计的,例如A/B串编码方法中,B串需同时遵循A串的约束条件和问题本身的约束条件,为此专门为B串的交叉操作设计了交叉算子,即保留顺序交叉,该交叉算子不仅具有很高的操作复杂性,还可能产生不可行解。 表2采用交叉算子的3个评价指标对前文所述的交叉算子进行了综合评价。表3所示为这些交叉算子对FJSP的5类染色体编码方法的适用性,其中符号“√”表示该算子适用于对应的染色体编码方法或子染色体。 表2 8类交叉算子对比 表3 5类染色体编码方法的交叉算子适用表 变异算子设计决定变异算子的操作(或计算)复杂性,并严重影响遗传算法的搜索性能。为增加遗传算法的搜索性能,变异算子设计同样需考虑局部搜索能力和全局搜索能力。其中,局部搜索能力指变异操作对父代染色体的扰动应尽可能地小,从而提高局部搜索能力,有利于遗传算法快速收敛,例如智能变异就具有很强的局部搜索能力;全局搜索能力指变异操作对父代染色体产生的变动应尽可能地大,从而提高群体的多样性,有利于扩大遗传算法的搜索能力,例如倒序变异就具有较强的全局搜索能力。就变异算子的操作复杂性而言,变异算子设计越简单,变异操作的复杂性越低,算法的整体计算效率越高。一般经典变异算子的执行过程相对简单,而针对特定编码方法设计的变异算子的执行过程相对复杂。在6类变异算子中,除交换变异、插入变异和倒序变异是经典变异算子外,其他均为适应FJSP及其特殊编码方法设计,其操作过程更加复杂。 表4 6类变异算子对比 表4采用变异算子的3个评价指标对前文所述的变异算子进行了综合评价。表5所示为这些变异算子对FJSP的5类染色体编码方法的适用性。 表5 5类染色体编码方法的变异算子适用表 表6 5类编码方法对比 (1)编码可行性 编码可行性指基于某种染色体编码方法生成的染色体总能解码成一个可行的调度方案。显然,在上述5类编码方法中,仅A/B串编码不能保证所生成的任意染色体能够解码成一个可行的调度方案。 (2)编码空间与解空间的映射关系 映射关系通常有1-to-1,1-to-n,n-to-1映射3种。对于染色体编码方法而言,编码空间与解空间的映射关系必须保证唯一性,即一条染色体只能解码成一个特定的可行调度方案,虽然1-to-1映射和n-to-1映射都满足唯一性,但是n-to-1映射存在多条染色体可解码成同一种调度方案的情况,这会降低搜索性能[70],因此1-to-1映射被认为是编码空间与解空间最期望的映射关系。显然,在半主动调度下(对于其他调度类型,映射关系可能发生变化),除A/B串编码是1-to-1映射外,其余编码方法均属于n-to-1映射。 (3)染色体存储空间 染色体存储空间指存储一条染色体所需的空间,其与染色体的数据结构密切相关。在以上5类编码方法中,MSOS-I和A/B串编码的染色体存储空间最小,一条染色体需要2T个“整数”存储空间(0,1,以及工序号和机器号均看作为一个整数)。 (4)解码复杂性 解码指将编码空间中的一条染色体转换为解空间中一个调度方案的过程。在5类编码方法中,表格编码生成的染色体不需要解码,因为表格编码已经运用相关的调度规则对给定的机器分配进行了调度计算,即表格编码中的译码分配表本身就是一个调度方案,而其他4类编码方法均需解码才可以得到调度方案。 (5)编码完备性 编码完备性指任意调度方案均能在编码空间中找到与之对应的染色体,这是保障遗传算法求解质量的关键。显然,在5类编码方法中,表格编码方法因为采用调度规则解决FJSP的调度子问题无法保证找到所有可行调度方案(包括最优解),所以不具备编码完备性。 (6)遗传操作复杂性 遗传操作越简单,执行效率越高,算法的整体计算效率相对越高。由表2~表5的分析结果可知,MSOS的遗传操作最简单。 (7)遗传操作多样性 染色体编码方法可应用的交叉和变异算子越多,特别是经典的交叉和变异算子越多,越具有遗传操作多样性,可借此提高遗传算法的性能。由表3和表4可知,MSOS可使用的交叉和变异算子的种类最多,因此具有较好的遗传操作多样性。 综上可知,MSOS是5类染色体编码方法中综合性能最好的一类编码方法,特别是MSOS-I编码可以保证编码可行性,且存储空间小,相应的遗传操作简单多样,运用这种染色体编码方法的遗传算法通常表现出较高的性能,目前MSOS-I编码方法已经成为求解FJSP遗传算法中使用最多的编码方法。 遗传算法是求解FJSP使用最广泛的方法,在过去30年,研究者通过改进遗传算法的各个要素提升了其求解FJSP的性能。本文聚焦遗传算法的染色体编码方法,详细介绍和分析了求解FJSP的5类主要染色体编码方法,并结合这些编码方法适用的交叉和变异算子,从7个维度对这些编码方法进行了评价。综述结果表明,MSOS-I编码是遗传算法求解FJSP较好的染色体编码方法,其染色体结构简单,并可选用较多类型的交叉和变异算子。 基于在染色体编码方法和遗传算子方面对遗传算法求解FJSP的讨论,未来研究可侧重于改进现有染色体编码方法或设计新的染色体编码方法,在保证其结构简单、编码具有可行性和完备性的前提下,尽量使其适用于经典的交叉和变异算子,以降低遗传操作的复杂性,提高遗传操作的多样性。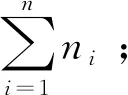
2.2 三元组编码
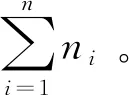

2.3 表格编码
2.4 矩阵编码
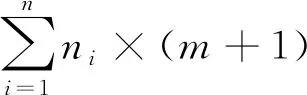
2.5 A/B串编码
3 遗传算子
3.1 交叉算子

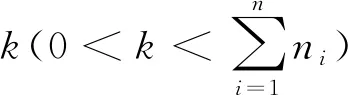
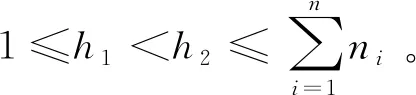

3.2 变异算子

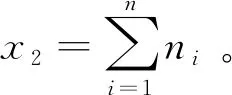

4 讨论
4.1 交叉算子的评价
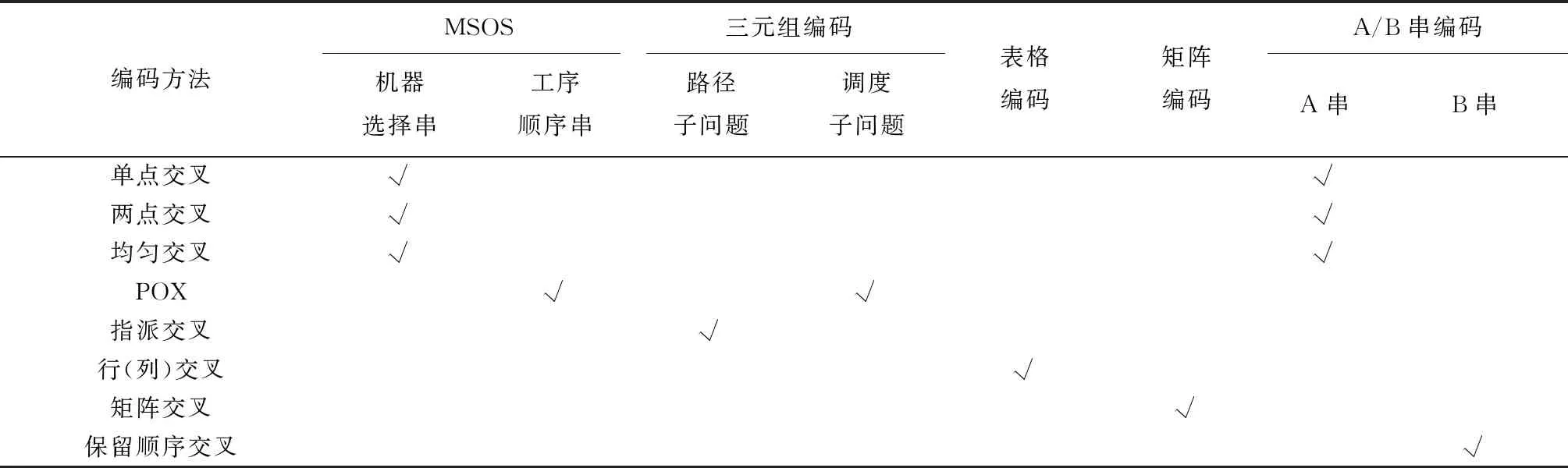
4.2 变异算子的评价
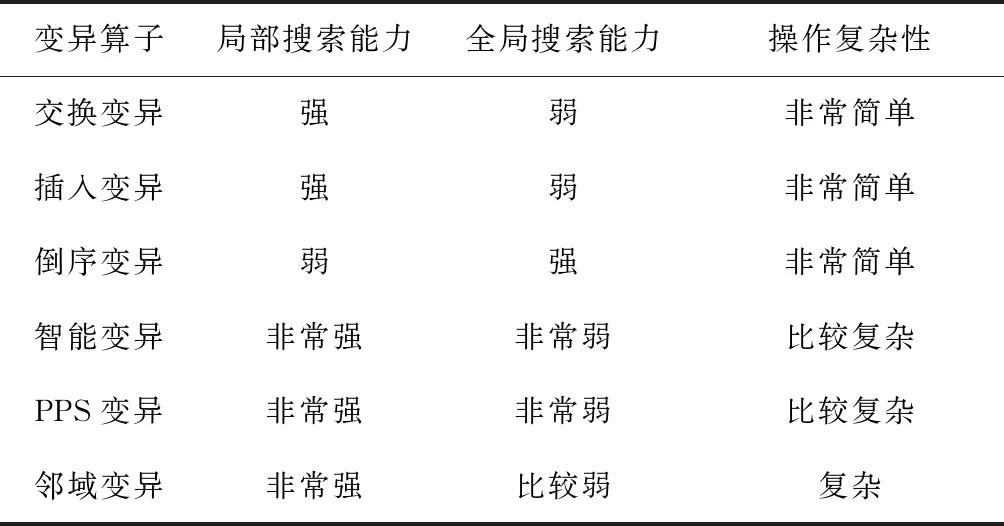

4.3 染色体编码方法的评价
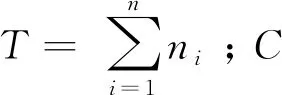
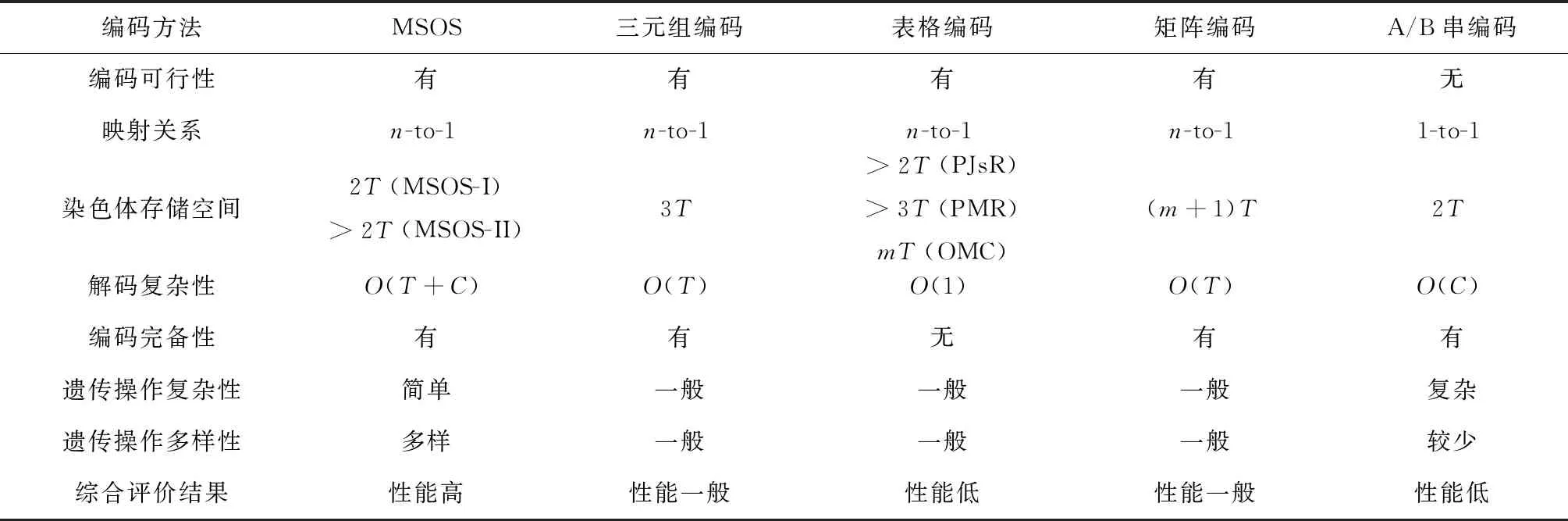
5 结束语

