渗碳Cr-Ni高强硬度合金钢超高周疲劳寿命预测

李明凯,赵雄翔,康贺铭,李永平,于 欢,邓海龙,2

(1.内蒙古工业大学 机械工程学院，呼和浩特 010051； 2.内蒙古自治区先进制造技术重点实验室，呼和浩特 010051； 3.内蒙古自治区能源技术中心，呼和浩特 010051)

高强硬度合金钢作为工业生产中的重要金属材料,在汽车、船舶以及航空航天等关键领域发挥着重要作用[1]。其中，Cr-Ni高强硬度合金钢多适用于承受重载及冲击载荷的工况下,为了满足其在强度、韧性以及寿命等方面的要求,表面强化工艺如渗碳[2]、激光喷丸[3]、高频淬火等已被广泛采用。然而,随着超高周次工况下失效问题的频频发生[4],传统的疲劳寿命预测以及强度预测评估已经不再适合当今的设计和生产实际。为了更好地把握合金钢在超高周次载荷下的疲劳失效规律,对长寿命条件下的合金钢疲劳特性及强度预测评估方法进行研究具有重要意义。

合金钢经表面强化处理后,S-N曲线常呈独特的“阶梯状”或“双线性”[4-6],即失效往往由表面向内部转变。对于内部失效,裂纹的产生主要由冶金缺陷引起,如非金属夹杂物或非均匀组织等[7]；当载荷循环次数大于约106时,由于受夹杂物周围的局部应力影响,其附近会产生一个特殊区域,Sakai等人[8]称该区域为“细颗粒区(Fine Granular Area, FGA)”。而根据断口处有无FGA特征,又可将内部失效划分为长寿命区和短寿命区。

总之,在循环加载过程中,FGA的形成消耗了超过90%的超高周疲劳寿命[9],并决定了材料的超高周疲劳表现。为了更好地研究材料的疲劳特性,须充分的考虑夹杂尺寸以及FGA特征尺寸对疲劳失效的影响。

随着生产实际对成本、性能以及寿命要求的愈加苛刻,材料的强度及寿命问题已经成为国内外学者关注的重点,并由此产出了一系列有关疲劳寿命强度的预测模型。Murakami等人[10]基于维氏硬度和夹杂尺寸,提出了疲劳极限预测模型；Wang等人[11]基于Murakami模型,提出了一种考虑断裂循环次数的寿命预测模型；Gao等人[12]结合裂纹扩展速率,提出了一种包含疲劳强度评估和裂纹扩展速率表征的疲劳强度预测模型；张拓等人[13]结合材料退化规律,提出了一种变幅载荷下线性疲劳寿命预测模型；孙振铎等人[14]基于极值分布函数,构建了一种与夹杂尺寸相关的疲劳强度预测模型；Deng等人[4]基于累积损伤法,提出了一种虑及夹杂尺寸-FGA-鱼眼型疲劳强度预测模型。

然而,基于累积法，并同时考虑应力比、 FGA应力强度因子、 FGA尺寸以及夹杂尺寸等重要参数的疲劳寿命预测模型还较少。

本文在应力比分别为0和0.3两种情况下,对渗碳Cr-Ni高强硬度合金钢的超高周疲劳特性开展研究。基于内部失效机理,结合累积损伤理论,对合金钢疲劳寿命模型进行预测评估,通过与试验结果的对比分析,验证了本文寿命预测模型的可行性。

1 实 验

1.1 材料与试样

本文选用Cr-Ni高强硬度合金钢作为疲劳试验材料,其化学成分如表1所示。首先将原始棒料加工成较为粗糙的沙漏状,再采用360～2 000目的砂纸沿其轴向打磨至光滑,试样的最终形状及尺寸如图1所示。为了符合试验条件,须对试样表面作渗碳处理,并将渗碳后的试样置于840 ℃的真空环境中油淬45 min,然后在160 ℃的空气中进行低温回火90 min,以完成最终的热处理工艺。

表1 合金钢的化学成分(质量分数/%)

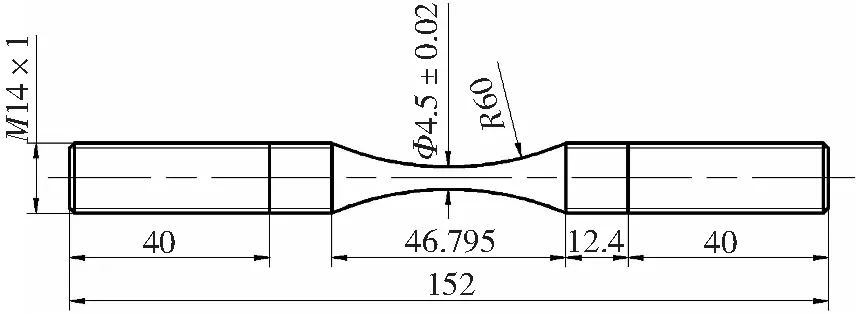
图1 试样形状及尺寸(单位：mm)

1.2 组织和性能测试

室温下,在试样(热处理工艺后)断口的最小截面处获取金相试样,将金相试样使用砂纸打磨平整,使用体积分数4%的硝酸酒精溶液进行浸蚀。利用JSM-6610LV扫描电镜(SEM)对处理后的金相试样进行微观组织观测；在室温下通过MTS809测试系统对渗碳Cr-Ni高强硬度合金钢进行单调拉伸试验，保持拉伸速率为5 mm/min。

1.3 疲劳试验方法

在室温下,使用高频疲劳测试机(QGB-100)对试样进行轴向载荷下的超高周疲劳试验,选取0和0.3两种不同的应力比,试验频率均为100 Hz。当应力比为0时,施加的最大与最小应力幅值分别为650、500 MPa；当应力比为0.3时,施加的最大与最小应力幅值分别为507.5、437.5 MPa。试验过程中,当试样发生完全破坏或载荷循环周次达108时,则试验终止。考虑到时间以及成本条件等多个方面的限制,在应力比为0时,记录有效数据11组；应力比为0.3时,记录有效数据5组。疲劳试验结束后,利用SEM对各失效试样进行断口表面观测。

2 结果与分析

2.1 微观组织和力学性能

试样微观组织如图2所示。可见,试样渗碳层和基体的微观组织有很大区别：在渗碳层中,微观组织以残余奥氏体和针状马氏体为主；而在基体中,微观组织主要呈现为板条马氏体；两者中均可发现非金属夹杂的存在。同时，基于MTS809测试系统，最终测得试样的抗拉强度σb约为1 780 MPa[15]。

图2 试样金相组织

2.2 S-N曲线

在应力比分别为0和0.3时,渗碳Cr-Ni高强硬度合金钢关于应力幅值与疲劳寿命的关系如图3所示。在应力比不同时,试样出现内部失效的循环次数均高于106,而出现表面失效的循环次数均小于5×105,符合内部失效多发生于长寿命区,表面失效多发生于短寿命区的普遍结论；在应力比相同时,两种失效模式下的试样疲劳强度均随着疲劳寿命的增加呈现递减趋势。在疲劳寿命相同时,无论在何种失效模式下,应力比为0时的试样疲劳强度总是大于应力比为0.3时的试样疲劳强度。对于表面失效，通过线性拟合得到应力比为0和0.3时的疲劳极限(即未出现表面失效模式的最低应力)分别为600和473 MPa；而对于内部失效，由于“无穷多次”应力循环在试验中是难以实现的，故基于高频振动实验法，本文将条件疲劳极限定义为循环次数达到108时所对应的疲劳强度[15],应力比为0和0.3时的疲劳极限分别为490和374 MPa。

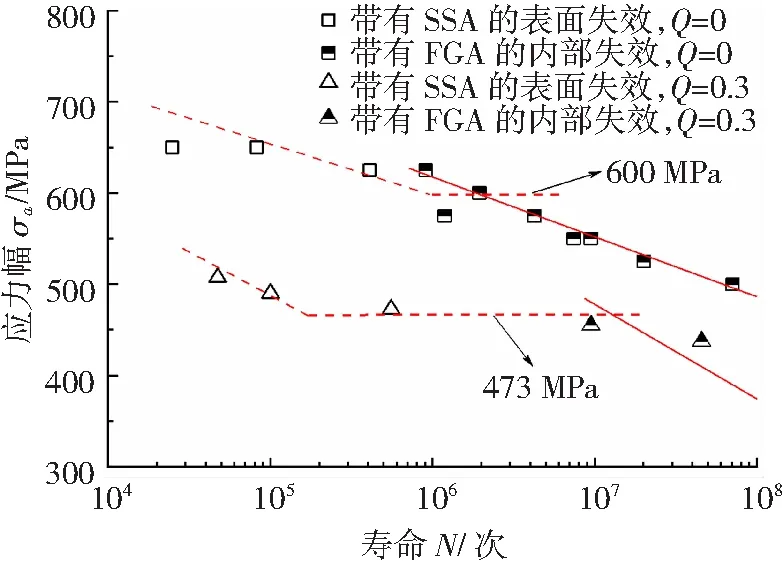
图3 应力比为0和0.3时渗碳Cr-Ni高强硬度合金钢S-N曲线

2.3 断口观测和失效机理

通过SEM对所有的疲劳失效样本进行观测,其中典型的断口形貌如图4(图中Q均表示应力比)所示。根据疲劳裂纹萌生位置以及断口形貌,可将疲劳失效形式划分为带有FGA的内部失效和带有表面光滑区(Surface Smooth Area, SSA)的表面失效,并分别对应图4(a)、(b)、(e)、(f)以及图4(c)、(d)。其中,在分别作为内部失效和表面失效典型特征的鱼眼和SSA中,均发现了非金属夹杂的存在。因此,可以断定非金属夹杂对诱发疲劳裂纹萌生有着不可忽视的作用。

对于夹杂引发的内部失效,其失效机理可归结如下：在长期循环载荷作用下,夹杂物周围出现的应力集中不断导致晶粒细化,该过程中萌生的微裂纹经FGA向鱼眼扩展后,最终发生失效；而对于夹杂引发的表面失效,同样因为外加循环载荷以及表面残余应力的影响,在夹杂周围引发应力集中效应导致裂纹萌生与扩展,其中以夹杂为中心而形成的断口表面光滑区域称为SSA。不同于SSA内部,SSA外部的裂纹扩展相当迅速,其由于快速扩展而形成的放射裂纹所呈现出的椭圆形粗糙区域称为SRA(表面粗糙区),如图4(c)和(d)所示。

2.4 基于累积损伤理论的疲劳寿命预测模型构建

鉴于疲劳裂纹所形成的区域可近似于圆形,结合400倍率放大下的SEM图像及图形测量软件Image J所得到的相关裂纹参数如下：Rinc-S,RSSA,Rinc,RFGA和RF,其分别作为表面夹杂、SSA、内部夹杂、FGA和鱼眼的半径。各裂纹尺寸和疲劳强度关系如图5所示。可见在不同应力比下,诱发失效的夹杂尺寸均与施加的应力比及应力幅无关,而其余各裂纹尺寸则随着疲劳强度的增加呈递减趋势。

图4 典型断口形貌SEM图

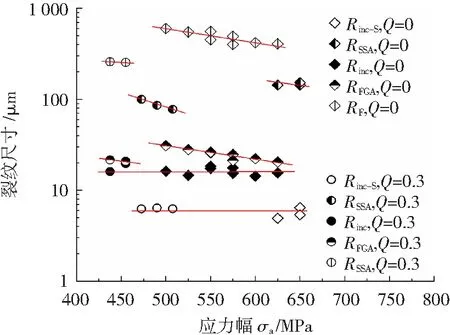
图5 各裂纹尺寸与σa的关系

基于内部夹杂、FGA以及鱼眼尺寸,可分别建立三者与相关应力强度因子ΔKinc、ΔKFGA与ΔKF之间的关系如下[16]：

(1)

同理,表面疲劳失效时的表面夹杂及表面光滑区的应力强度因子ΔKSD及ΔKSSA可表示如下[17]：

(2)

因此,ΔKFGA、ΔKSSA及ΔKF与疲劳寿命N的关系如图6所示。

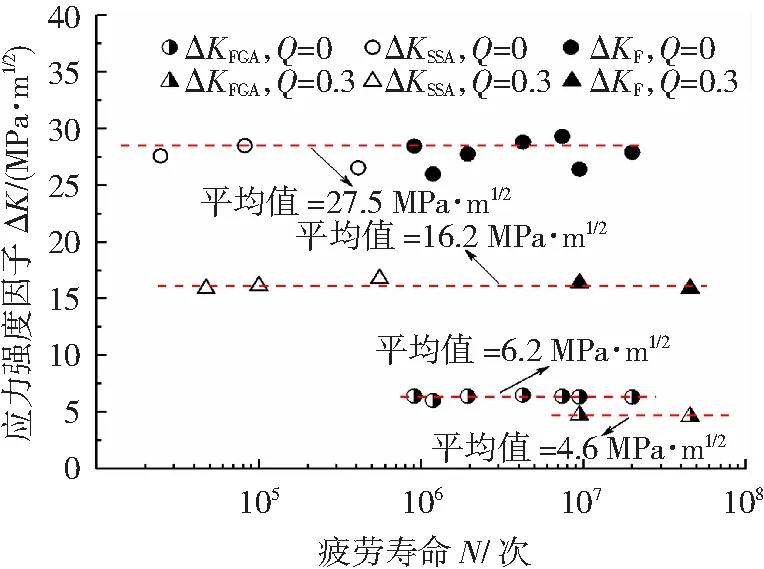
图6 各ΔK与N关系

由图6可知,同一应力比下的ΔKFGA、ΔKF和ΔKSSA的值几乎呈水平趋势,其随疲劳寿命的变化波动很小。当应力比为0和0.3时,ΔKFGA的值分别位于5.9～6.5 MPa·m1/2和4.5～4.7 MPa·m1/2之间,其均值分别为6.2 和4.6 MPa·m1/2。当应力比为0时,ΔKF和ΔKSSA的值的范围分别为25.9～29.3 MPa·m1/2和26.5～27.7 MPa·m1/2,其平均值非常接近,约为27.5 MPa·m1/2。当应力比为0.3时,ΔKF的值位于15.8～16.4 MPa·m1/2之间,ΔKSSA的值在15.8～16.7 MPa·m1/2之间,ΔKF和ΔKSSA的平均值也十分相近,约为16.2 MPa·m1/2。

由于长期循环载荷的作用,FGA内的疲劳裂纹从萌生到以夹杂为中心逐渐向外累积的过程,可认为是每次循环加载对试样产生微量损伤的叠加,故有以下关系式：

(3)

式中：RN为第n次加载后的损伤区半径；pn为第n次加载后损伤区半径增量与第n-1次加载后损伤区半径的比值。

引入与pn和疲劳寿命N相关的变量p以简化计算,其关系式如下：

(4)

故式(3)可改写为

RN=Rinc(1+p)N≥RFGA

(5)

基于式(3),可将RN与RFGA之间的关系简化如下：

RFGA=Rinc(1+p)N

(6)

通常，材料的疲劳强度与未经表面处理的抗拉强度密切相关。而对于渗碳合金钢，最大应力也会对其裂纹的萌生产生一定的抑制或者促进作用。因此，建立p、最大应力σmax以及抗拉强度σb的关系如下：

(7)

将式(6)、式(7)代入式(1)中,并引入拟合参数m和n,从而可将式(1)改为

(8)

式中,Nf为预测寿命。

基于疲劳试验数据,使用牛顿算法对式(8)中的参数m和n进行拟合,其中,当Q=0时,m0=2.75×10-3,n0=23.20；当Q=0.3时,m0.3=2.70×10-3,n0.3=39.10。试验寿命与预测寿命关系如图7所示。

由图7可知,在不考虑ΔKFGA以及Rinc为常量的情况下,预测寿命相对于试验寿命均在3倍因子范围内,因此该疲劳寿命预测模型具备较高的精度,即可作为超高周疲劳寿命预测的有效方法。然而，考虑到ΔKFGA及Rinc等参数在每次取得时均须在材料发生疲劳破坏后,因此该模型具有较大的局限性。

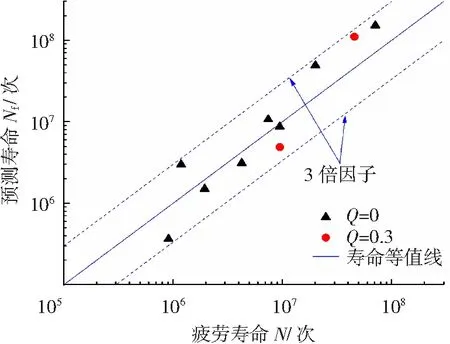
图7 基于内部失效的试验寿命与预测寿命

基于上述预测模型的不足,下文对其作出改进，从而提出第二种寿命预测模型。

由图5及图6可知,ΔKFGA及Rinc与材料的疲劳寿命以及所施加的应力无关,而取决于因冶金缺陷等因素而形成的材料固有属性。

因此,式(8)可进一步改为

(9)

表2 不同应力比下ΔKFGA及Rinc的均值

将表2中均值数据代入式(9)中,则基于均值参数及内部失效的试验寿命与预测寿命关系如图8所示。基于图8可知,改进后的寿命预测模型同样具有较高的预测精度。该模型将ΔKFGA以及Rinc取为固定常数,虽然绝大部分的预测值相对于试验值而言更加紧凑，但预测寿命在Q=0时的一点位于3倍因子之外，相对于前种寿命预测模型而言有较低的容错率，但仍属可接受的范围。同时,考虑到ΔKFGA及Rinc测量及计算的繁琐性,基于均值参数及内部失效的寿命预测方法更加简便，相对更容易被接受。

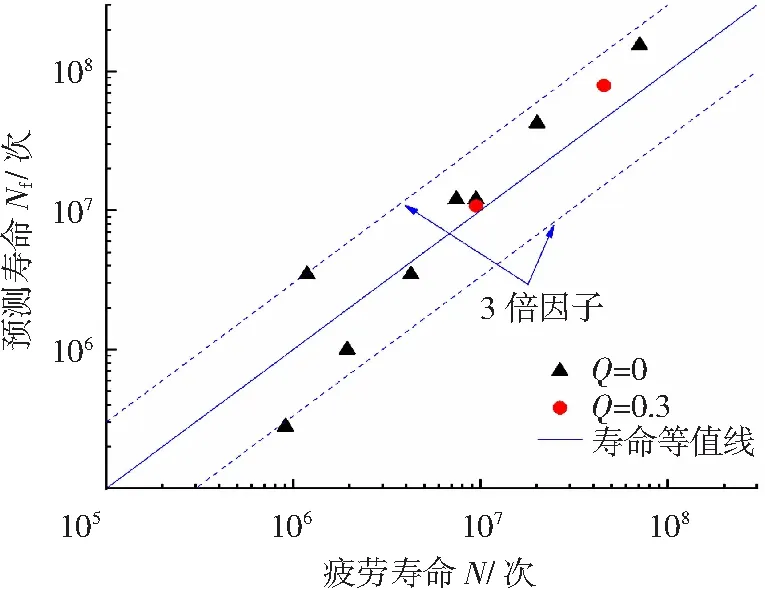
图8 基于均值参数及内部失效的试验寿命与预测寿命

3 结 论

1) 对应力比为0和0.3下的渗碳Cr-Ni高强硬度合金钢展开超高周疲劳试验,构建了不同失效模式时两种应力比下的S-N曲线。

2) 基于断口观测，无论内部失效还是表面失效，其失效机理如下：由于长期循环载荷的影响，于夹杂周围出现应力集中，并以夹杂为中心诱发裂纹的萌生与扩展，最终导致材料失效。

3) 基于累积损伤法,并考虑应力比、ΔKFGA、RFGA与Rinc等重要参数,建立了两种可适应不同应力比的渗碳Cr-Ni高强硬度合金钢疲劳寿命预测模型,经对比分析,不同参数条件下的两种预测模型均具有较高的预测精度,而基于均值参数及内部失效的寿命预测方法更加简便，且除极少数点外，预测值也更加紧凑精确，相对更容易被接受。