探究斜拉桥体系总体布置参数对受力性能的影响
张永顺
重庆交通大学/土木工程学院 重庆 400074
引言
在斜拉桥中,斜拉索对主梁提供了多点弹性支承,并将主梁所承受的荷载传递给主塔,再通过主塔将主梁荷载传至基础。塔柱以受压为主,斜拉索以受拉为主,主梁主要以受弯和受压为主。跨度较大的主梁与多点弹性支承连续梁的工作状态较为类似。由于主梁要承受斜拉索水平分力的作用,主梁截面的基本受力特征多表现为偏心受压,相对于梁式桥,主梁尺寸大大减小,结构自重显著减轻,大幅度提高了斜拉桥的跨越能力。塔柱、拉索和主梁构成了稳定的三角形,斜拉桥的结构整体刚度故而较大。
在自锚式斜拉桥中,边跨计算跨径与主跨计算跨径的比值(边中跨比)Ls/Lc、梁宽与主跨计算跨径的比值(宽跨比)、桥面以上的索塔高度与主跨计算跨径的比值(塔跨比)h/Lc等,这些布置参数就是影响斜拉桥受力性能的总体布置的主要性能参数,同时又与建设成本有着紧密的联系,下面将进行详细阐述。
1 总体布置参数
1.1 边中跨比
双塔斜拉桥体系的边中跨比是一个重要参数,一般情况下其取值根据桥位的通航要求和地质水文资料来确定,同时还应考虑由此带来的对力学性能和经济性能的影响。从力学性能看,边中跨比主要与桥面恒、活载比例以及塔梁抗弯刚度等因素有关,同时还和斜拉索的轴向刚度、结构体系,以及斜拉索的布置方式等因素相关,桥塔与主梁之间不同的连接体系。例如漂浮体系、固结体系以及支承体系等,都会对边中跨比的合理取值有一定影响。当边跨跨径较小时,结构整体刚度会随之增大,边跨对索塔的锚固作用增大,与此同时边跨平衡活载上拔力的能力也会随之减小;边跨跨径增大时,锚墩负反力就会变小,但结构整体刚度就会相应降低;当边跨跨径过长时,某些缆索甚至会退出工作。
一般中小跨径斜拉桥公路桥梁中,当锚索应力比在0.4∶1时,随着跨径的增大桥面的活载与恒载的比值会显著变小,钢桥面边跨与主跨跨径之比控制在0.35~0.39之间,组合梁桥面边跨与主跨跨径之比控制在0.40~0.45之间,而预应力钢筋混凝土桥面则是控制在0.46~0.50之间时最为适宜。超大跨径斜拉桥一般采用边跨部分长度内分散锚固锚索的方式,以避免端锚索规格过大造成的施工难题。如苏通大桥中跨加载时,边跨靠外侧约半数的斜拉索参与抵抗索塔向中跨的侧向变形,已看不出明显的端锚索作用,拉索的应力幅不大,锚索的应力变化幅值不再是控制缆索设计的关键,边中跨比限值由此得以放宽。
1.2 主梁宽跨比
主梁宽度变化对斜拉桥整体性能的影响也比较明显,主梁宽度的增加会使主梁侧向刚度相应增加,由此可以显著减小横向静阵风作用下主梁中跨跨中的侧向位移,并能有效提高结构面外屈曲稳定性,还可提高结构的抗风颤振稳定性,从而改善结构的抗风性能。如果增加加劲梁宽度,结构横向刚度就会随之明显增加。因此,由横向风荷载引起的加劲梁侧向位移会迅速降低,外腹板应力也会随之迅速降低,同时成桥恒荷载状态下的加劲梁面外稳定性也会随之显著提高。同时还表现在加劲梁一阶侧弯频率的变化上,对结构的长期效应更加有利。
但是,加劲梁宽度的增加对一阶扭转频率的提高是有不利影响的。虽然增加桥面宽度明显,可以使截面的扭转刚度得到提高,但是同时也使得桥面自身质量大大提高,桥面附加荷载、横隔板等附加质量所产生的质量惯性矩,将会导致结构扭转振型比未增加加劲梁宽度之前提前出现。换而言之,加劲梁宽度增加所带来扭转刚度增加对结构有利的“贡献值”,不能抵消由宽度增加所带来附加质量对结构扭转频率的“损耗值”。一般情况下,加劲梁宽度每增加5m时,一阶扭转频率就会降低5%左右。但又反之,桥面宽度的增加虽然对扭转频率不利,却可以显著提高结构整体的颤振稳定性。其原因在于,根据‘Standard Strip Analysis’(螺旋桨片条理论),结构的颤振临界风速,可以认为与扭转频率和桥面宽度的乘积成正比,扭转频率受加劲梁宽度变化时的影响程度,将会滞后于桥宽自身的线性变化率[1]。
1.3 索塔塔跨比
索塔塔跨比是影响斜拉桥结构的一个较为重要的力学性能参数。索塔高度过大,拉索的水平倾角必然变大,反之,拉索水平倾角会变小。索塔高度的变化可以说直接改变了拉索的水平倾角,随之必然会改变结构的竖向支承刚度,进而影响索塔、主梁、拉索的内力分布情况和变形状态。研究表明,索塔高度变化对结构主梁的轴力、竖向挠度、竖向弯矩、侧向位移、侧向弯矩、屈曲稳定系数以及索塔塔顶位移、纵向弯矩等力学性能均有影响。增加索塔高度可相应减小主梁的轴力和活载响应,还会显著减小主梁的竖向挠度和竖向弯矩,同时会减小索塔的纵向最大位移和弯矩,但又会随之降低主梁的屈曲稳定性。此外,横向静阵风作用下,索塔高度变化对的主跨主梁跨中处的侧向弯矩和位移影响较小,但仍表现为随索塔高度的增加,主梁的侧向弯矩和侧向位移逐渐增加。
在横向风荷载作用下,塔跨比对超大跨径斜拉桥的影响较小。这是因为横向风荷载作用下索塔上风荷载在贡献中的比例很小,一般小于0.05,主要表现在斜拉索上的风荷载,其次为主梁上的风荷载。降低塔高必然会减小了拉索长度,但同时又会使得斜拉索外径(规格、面积)相应增加,导致横向静风总效应变化不大。塔跨比越小,以索塔刚度变大,结构整体稳定性必然得以提高,但又由于主梁的轴向力增加,无论是主梁的面外还是面内屈曲,其弹性稳定性均会明显下降,按原主梁截面参数必然不能满足结构稳定性要求。
1.4 塔上锚索间距
塔上锚索间距的变化,也可表征为拉索角度的改变。在塔跨比相同的条件下,塔上斜拉索的间距越大,内测的短索上端的锚固点就会降低,斜拉索与铅锤面的角度就会随之增大,从而就使得部分斜拉索索力增大,但是增大塔上斜拉索间距对于外侧长斜拉索的索力影响较小。研究表明,在恒载长期作用下,主梁靠近索塔区的轴向力的总体效应会增加0.13左右。
当固定斜拉桥塔跨比,增大塔上斜拉索间距,使得内侧部分斜拉索与水平面夹角减小后,边跨跨中区域的竖向刚度会迅速降低,活载所产生的结构响应(例如位移)明显增大。而中跨跨中部位竖向刚度,主要受到索塔上外侧长斜拉索的控制,斜拉索角度变化较小时,活载挠度影响也相对较小。而梁端水平位移以及塔的侧向位移,主要是由边跨和中跨的活载加载时斜拉索水平分力的增量所导致,并对塔上锚固区变化相对比较敏感。在塔跨比相同的条件下,恒载作用下塔上索距增大会使得主梁靠近索塔区的轴力会增大;边跨跨中区域竖向刚度降低,对中跨跨中活载竖向挠度的影响相对较小,梁端水平及索塔侧向位移会显著增大;可减小塔底处顺桥向所产生的弯矩响应,从而降低了结构整体稳定性[2]。
2 调整斜拉桥体系受力性能的方法
在斜拉桥设计时,各项力学指标都应控制在合理范围内,作为桥梁工程设计者而言,仍然需要辩证且敏锐地看待斜拉桥的各项力学参数。当某项指标不满足设计要求时,就需要调整结构参数来使其满足设计要求。此处以飘浮体系自锚式斜拉桥为例,用线性理论分析各主要力学指标与结构参数之间的关系,以期讨论斜拉桥体系各受力性能的调整方法。
2.1 主梁轴力
在均布荷载作用下,根据主梁上轴力边界条件假设,主梁任意一点处的轴力可由下式表达:
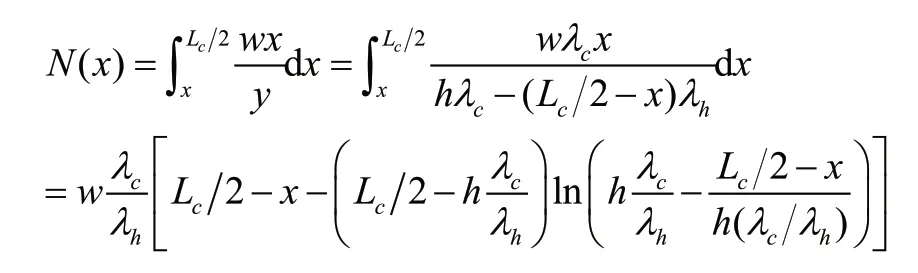
上式中,h为索塔的有效高度,LC为中跨跨径,λc和λh分别为主梁中跨的平均索距以及索塔顶的索距,w为主梁上的均布荷载集度。由上式可以看出,在外部荷载、主跨跨径一定的情况下,影响主梁轴力的主要参数有:索塔有效高度h、拉索在主梁中跨的平均索距和索塔顶的索距的比值λc/λh。
通过分析表明,索塔的有效高度是主梁轴力的重要影响因素之一,索塔有效高度越大,主梁的轴力减小的程度就会越明显。拉索在主梁中跨的平均索距和索塔顶的索距的比值,对主梁轴力的影响相对于索塔有效高度较小。因此,为了降低主梁的轴力以及轴力所带来的力学效应,可以适当增加索塔的有效高度[3]。
2.2 索塔塔顶位移
我们知道,三跨连续梁相同的均布荷载量值作用下,仅在中跨布载时的中跨跨中竖向位移要比在三跨全部满载时中跨竖向位移大。那么显然在斜拉桥中,中跨满载时的索塔顶部水平位移时最大的。而当端锚索所提供的力值明显时,塔顶的水平位移可由下式表达:
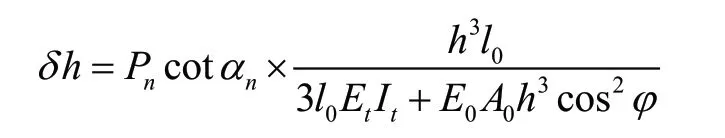
上式中,δh表示塔顶的水平位移,Pn为拉索在主梁处的竖向力,αn表示第n根斜拉索的水平倾角,Et和It分别为索塔的弹性模量以及惯性矩。在外部荷载一定的情况下,影响索塔塔顶的水平位移主要参数有索塔的抗弯刚度、边跨尾索的刚度以及索塔的有效高度。由上述公式可以看出,边跨尾索的刚度对索塔顶部水平位移影响最大,索塔的有效高度次之,而索塔的抗弯刚度相对于前两者影响较小。由此表明,在外部荷载一定的情况下,可以适当地增加边跨尾索刚度,以期减小索塔顶部的水平位移[4]。
2.3 主梁屈曲稳定系数
主梁的平面内屈曲性态,可以近似的简化为一根两端铰支的弹性地基梁来计算,临界压力由下式表示:
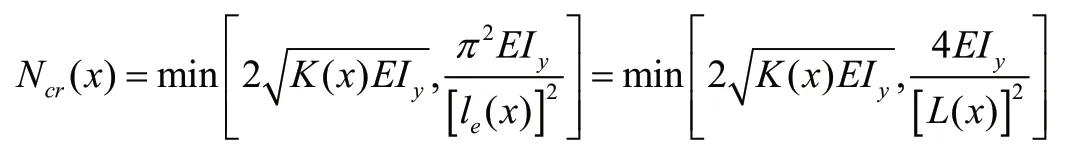
上式中,le为主梁屈曲的有效长度,L(x)为在支承刚度为K(x)的情况下的弹性地基梁的特征长度。由此,定义主梁的屈曲安全系数为:
在外部荷载一定的情况下,主梁线性屈曲稳定系数与索塔的有效高度、边跨尾索的刚度、中跨外索的刚度、主梁拉索的索距、索塔的抗弯刚度以及主梁的抗弯刚度等因素有关。索塔的有效高度是主梁屈曲稳定系数的最为重要的影响因素,主梁的抗弯刚度以及拉索在主梁上分布的索距对主梁屈曲稳定系数的影响次之,而由索塔的抗弯刚度和拉索的刚度所引起的对主梁屈曲稳定系数的影响相对较小。由此表明,若提高主梁的屈曲稳定系数,最为有效的措施是增加索塔有效高度以及主梁的抗弯刚度。同时,也可以通过减小梁上拉索索距的措施,来提高主梁的屈曲稳定系数[5]。
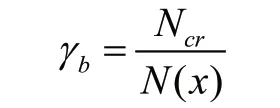
3 结束语
斜拉桥结构的各种参数(体系参数和总体布置参数)之间是相互影响、相互制约的。结构参数决定了结构的形状、荷载、构件抗力及其受力形态。本文通过探讨斜拉桥的边中跨比、主梁宽跨比以及索塔塔跨比等总体布置参数,对调整斜拉桥体系受力性能提出了几点方法:①适当增加索塔的有效高度,可以降低斜拉桥主梁的轴力效应;②在荷载一定的情况下,可通过增加边跨尾索刚度,来减小索塔顶部的水平位移;③通过提高索塔有效高度以及主梁抗弯刚度,可有效提高主梁的屈曲稳定系数。

