基于改进蝗虫算法优化Canny算子的鸡蛋裂纹图像检测

涂伟沪

蔡玲霞1

李学军2

(1. 新疆哈密广播电视大学，新疆 哈密 839000；2. 四川大学锦城学院，四川 成都 611731)

由于图像边缘检测具有非接触、无损伤、精度高等特点，正逐渐被应用于鸡蛋裂纹检测领域[1]。常用的图像边缘检测工具有Sobel算子[2]、Laplacian算子[3]、Prewitt算子[4]和Canny算子[5]等，其中，Canny算子因具有检测精度高、信噪比大、抗干扰能力强等优势，被广泛应用[6]。但是，Canny算子检测结果受双阈值、高斯函数滤波参数等影响较大，需反复调整参数，计算时间长，自适应鲁棒性差[7]。

李浩然等[8]利用直方图灰度局部方差对Canny算子阈值进行处理，一定程度提高了绝缘子裂纹检测准确率；李世雄等[9]采用图像梯度锚点对Canny算子进行优化，提升了检测边缘连续性；胡克满等[10]设计了具备不同参数的高斯滤波器，为不同检测类型选取对应滤波参数。上述研究改善了Canny算子伪边缘过多的问题，但是算法时间复杂性需进一步研究。随着群智能优化技术的不断发展，粒子群算法(PSO)、蚁群算法(AC)等智能算法被应用于边缘检测问题，樊石等[11]采用混合蛙跳算法对Canny算子双阈值进行优化，谢昕等[12]采用果蝇优化算法对传统Canny算子进行改进，张健等[1]将粒子群算法应用于裂纹图像检测等，都取得了良好的检测效果，但智能优化算法容易陷入局部极值、收敛精度不高等固有缺陷中，需进一步改进。文章拟提出一种采用改进蝗虫算法(GOA)优化Canny算子中双阈值、高斯函数滤波参数，自适应获取最优参数；设计改进的模糊C-均值算法(FCM)和自适应极值逆向学习、编码突变更新机制，以提升GOA全局收敛能力，并采用实例仿真验证所提算法的有效性，以实现高精度鸡蛋线形、网状裂纹检测。

1 改进蝗虫优化算法(GOA)

GOA是一种新型智能优化算法，其参考蝗虫种群集体觅食行为，通过模拟种群间个体相互作用，实现对目标位置搜索[13]。对于N维优化问题，设定GOA种群内有Q只蝗虫，每个个体Xi=(xi1,…,xiN)(i=1,…,Q)代表问题一个解。t时刻，Xi(t)更新式为：

(1)

α=αmax-t(αmax-αmin)/Tmax，

(2)

(3)

式中：

α——更新参数；

β——相互影响函数；

f——吸引强度参数；

l——吸引尺度参数；

G(t)=(gi1,…,giN)——当前种群最优解；

由GOA个体更新过程可知，Xi学习对象不仅包括自身位置和种群最优位置信息，还融合了其他所有个体之间的交互影响，具有很强的局部搜索能力，但是全局收敛能力不足[14]。当种群最优解在局部极值附近时，局部极值强大的吸引力导致算法容易陷入局部最优。为提升GOA全局深度收敛能力，提出改进的GOA算法(IGOA)：采用改进的模糊C-均值算法对蝗虫种群进行自适应聚类分析，据此对种群进行不同等级划分，并分别为不同等级内个体设计不同更新方式，以扩展算法深度搜索空间和全局寻优能力。

1.1 种群等级划分

(4)

隶属度矩阵：

U=[μik]C×Q，

(5)

式中：

C——聚类个数。

FCM是目前应用最为广泛的聚类算法之一，但其处理离群点、非球形簇数据聚类问题效果不佳，文献[15]采用高维映射函数Φ(x)替代传统欧式距离度量，即：

D(Xk,vi)=‖Φ(Xk)-Φ(vi)‖2=ΦT(Xk)Φ(Xk)-ΦT(Xk)Φ(vi)-Φ(Xk)ΦT(vi)+ΦT(vi)Φ(vi)=K(Xk,Xk)-2K(Xk,vi)+K(vi,vi)，

(6)

式中：

K(X,v)=ΦT(X)Φ(v)——核函数内积。

文献[16]指出，若K(X,v)满足Mercer条件，则不需要知道Φ(x)具体形式。

1.1.1 新距离度量函数 为进一步提升对离群点数据聚类效果，采用新的度量函数对Xk到vi的距离进行重新度量，即：

D′(Xk,vi)=K(Xk,Xk)d(Xk,Xk)-2K(Xk,vi)d(Xk,vi)+K(vi,vi)d(vi,vi)，

(7)

(8)

此时，聚类目标函数为：

(9)

式中：

m——模糊加权指数。

对于式(9)，令∂J/∂μik=0、∂J/∂vi=0，则：

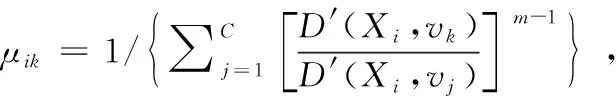
(10)

此时，通过迭代计算式(10)即可完成聚类分析。

1.1.2 聚类有效性指标 针对聚类个数C事先确定的缺陷，定义聚类有效性指标WB(C)：

(11)

式中：

nj——第j个分类样本数量。

w(i,j)——类内样本之间距离；

b(i,j)——类间离散程度。

WB(C)取值越小，聚类结果越好。设置C在[Cmin,Cmax]范围内依次变化，WB(C)取最小值对应的聚类个数即为最佳聚类个数Cbest。IFCM实现过程可以描述为：

参数初始化，聚类中心初始化，输入相关变量。

forC=CmintoCmax

While (终止条件不满足) do

{

根据式(9)计算J(U,V)，根据式(10)计算新的U、V；

}

根据式(11)计算WB(C)，更新聚类有效性指标集合{WB(C)}C=1,…,C；

C←C+1

end for

输出结果。

(12)

(13)

式中：

剩余个体组成蝗虫子族群G2(t)。

1.2 自适应极值逆向学习和编码突变

1.2.1 自适应极值逆向学习 选取G1(t)内N(t)个个体，执行极值逆向学习操作，即

Xi(t+1)=A+rand(0,1)×[B-Xi(t)]Xi(t)∈G1(t)，

(14)

(15)

式中：

A、B——Xi(t)下边界和上边界；

Nmax、Nmin——N(t)取值范围；

τ、ε——控制参数。

由式(14)、式(15)可知，进化初期种群个体差异性较大，G1(t)选取少量个体执行逆向学习，进化后期，种群进化区域停滞，选取较多个体进行逆向学习，扩展搜索空间。

1.2.2 编码突变 对G3(t)内个体执行编码突变操作，即：

Xj(t+1)=0.5[1+rand(0,1)]Xi(t)+0.5[1-rand(0,1)]Xk(t),Xi(t)∈G1(t),Xk(t)∈G2(t),Xj(t)∈G3(t)，

(16)

式中：

Xi(t)、Xj(t)、Xk(t)——3个个体隶属不同分类。

由式(16)可知，G3(t)内个体随机选取不在同一类的个体执行编码突变操作，即快速学习种群内优秀个体信息，又考虑不同子族群的空间差异性，提升了算法收敛效率。

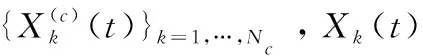
(17)

(18)

式中：

Nc——第c个分类样本数。

由式(17)、式(18)可知，将传统GOA个体间影响对象限制分类内，很大程度地避免了陷入局部极值。改进的蝗虫优化算法(IGOA)实现过程如图1所示。

图1 IGOA实现流程图Figure 1 IGOA implementation flow chart

2 Canny算子改进

2.1 传统Canny算子

Canny算子采用双阈值，对噪声抑制、边缘连接具有良好的效果[17]。其图像检测步骤为：

(1) 高斯平滑滤波。对于原图像I(x,y)，采用高斯滤波器G(x,y)进行卷积处理，得到平滑后的图像H(x,y)：

H(x,y)=G(x,y)×I(x,y)，

(19)

(20)

式中：

σ——标准差。

(2) 梯度方向和梯度幅值计算。对H(x,y)图像进行梯度方向θ(x,y)和梯度幅值A(x,y)计算：

(21)

(22)

(3) 非极大值抑制。对A(x,y)进行非极大值抑制操作，若A(x,y)比θ(x,y)方向相邻像素幅度值小，则A(x,y)归零；若幅度值大，则点(x,y)为可能边缘点。

(4) 阈值选取。设定高阈值TH、低阈值TL，若点(x,y)的A(x,y)≥TH，则该点为边缘点；若A(x,y)≤TL，则该点不是边缘点；若TL≤A(x,y)≤TH，则通过8领域像素判定法[12]确定是否为边缘点。

Canny算子存在以下缺陷：① 过分依赖高斯平滑滤波处理器，σ设置尤为关键。σ取值越大，容易丢失边缘信息，取值越小，容易检测出虚假信息。②TH、TL需事先人为设定，需经过大量试验和经验值判定，往往存在较大误差。

2.2 IGOA改进Canny算子

针对Canny算子固有缺陷，提出IGOA改进Canny算子(IGOA-Canny)，定义最大类间方差目标函数，设计多类蝗虫个体编码，以实现最优参数自适应获取。

2.2.1 目标函数 采用目标与背景之间的类间方差作为IGOA目标函数：

f[X(t)]=ω0(t)×ω1(t)×[λ0(t)-λ1(t)]2，

(23)

式中：

ω0(t)——A(x,y)≤TH的像素数量；

ω1(t)——A(x,y)>TH的像素数量；

λ0(t)——A(x,y)≤TH的像素平均灰度值；

λ1(t)——A(x,y)>TH的像素平均灰度值。

类间方差取值越大，区分目标与背景的正确率越高。对于TL，参考文献[18]，设定TL=TH/2.5。

2.2.2 多类个体编码 定义多类IGOA个体编码，将高斯函数方差σ、高阈值TH、低阈值TL、聚类中心V等效为个体编码，即：

(24)

2.3 Canny算子改进以及鸡蛋裂纹检测实现

根据IGOA个体编码定义方式，将IGOA优化Canny算子参数分为两个部分：① 执行IFCM操作对种群聚类分析，此时只对个体编码V部分进行更新操作，蝗虫个体执行基本GOA更新，完成一定次数迭代后，得到种群聚类分析。② 执行种群更新操作，此时只对个体编码(σ,TH,TL)部分进行更新操作，个体根据所在等级位置，分别执行自适应极值逆向学习、编码突变和分类内交互影响更新，最终得到Canny算子最优参数配置，最后采用改进的Canny算子对鸡蛋裂纹进行检查。

IGOA初始化复杂度为O(QN)，每执行一次IFCM操作复杂度为(Cmax-Cmin)tmaxO(QN)，种群完成一次更新复杂度为O(QN)，故IGOA计算复杂度为：

Tmax[O(QN)+(Cmax-Cmin)tmaxO(QN)]+O(QN)≈Tmax(Cmax-Cmin)tmaxO(QN)，

(25)

式中：

tmax——最大迭代次数。

基于IGOA-Canny的鸡蛋裂纹检测实现过程如图2所示。

图2 基于IGOA-Canny的鸡蛋裂纹检测过程

3 仿真试验

3.1 IGOA收敛性能验证

表1 测试函数Table 1 Test functions

由表1和图3可知，收敛精度上，对f1、f2、f3、f44个函数，无论是收敛精度还是收敛成功率，IGOA均优于其他3种算法，特别是对于复杂多极值、病态函数f3、f4，IGOA几乎都能够达到100%的成功率。运算效率上，IGOA能够以较少的迭代次数实现全局最优解求解，但是由于IGOA在每次迭代过程中叠加了模糊聚类操作，导致算法运算时间长于其他3种算法，可以采用并行计算以提高收敛效率。典型测试函数仿真结果表明，IGOA收敛精度更有优势。

图3 函数收敛曲线Figure 3 Function convergence curve

3.2 鸡蛋裂纹实例检测

为验证文中所提检测算法有效性，对鸡蛋线形裂纹和网状裂纹进行检测，试验选取100个大小不同、无明显破损、有标号的鸡蛋作采样检测(经仔细人工检测线形裂纹鸡蛋55个，网状裂纹鸡蛋45个)。选取基本Canny算子、文献[5]提出的ACO-Canny算子，文献[11]提出的SFLA-Canny算子和经典的Prewitt算子进行对比试验。采用文献[12]提出的漏检率作为评价指标，不同检测算法对鸡蛋线形、网状裂纹典型案例检测视觉效果见图4、图5，漏检率和算法运算时间对比结果见表3。

图4 鸡蛋线状裂纹检测视觉效果图Figure 4 Visual effect of egg linear crack detection

图5 鸡蛋网状裂纹检测视觉效果图Figure 5 Visual effect diagram of egg mesh crack detection

表3 不同检测算法裂纹漏检率、运算时间对比Table 3 Comparison of crack missed detection rate and operation time of different detection algorithms

由图4、图5和表3可知，裂纹漏检率方面，无论是对于线状裂纹还是网状裂纹，文中检测算法、SFLA-Canny算子和SFLA-Canny算子都表现出了良好的检测效果，且文中检测算法的漏检率更低，分别降低了约21.4%～31.2%，63.2%～69.7%，而基本Canny算子、Prewitt算子表现效果不理想，特别对于网状裂纹检测，漏检率均超过了50%。算法运行时间方面，由于IGOA在每次迭代过程中都要执行聚类分析操作，导致算法在运行时间上要慢于其他4种检测算法，后期可采用并行计算技术提升运算效率。试验结果表明，改进FCM的引入和重新定义种群等级、编码类型和更新方式，提升了改进蝗虫优化算法的全局收敛性能，而采用改进蝗虫优化算法优化参数配置的Canny算子，对鸡蛋裂纹检测具有更好的检测结果。

4 结论

提出了一种采用改进蝗虫算法优化Canny算子的鸡蛋裂纹检测方法。结果表明，通过设计改进模糊C-均值算法、重新定义蝗虫种群等级、编码类型和更新方式，以及自适应获取Canny算子最优参数，可实现对不同类型鸡蛋裂纹的有效检测，具有一定意义的推广应用价值。后续将重点围绕提升检测速度问题，研究采用并行运算技术以提高检测时效性。