基于原型学习与深度特征融合的脑功能连接分类方法研究

梁玉泽 冀俊忠 ,

人类大脑是一个高度复杂的系统,通过脑区之间的互相协作来完成特定任务.这种协作方式可以通过定量地分析静息态功能磁共振成像(Restingstate functional magnetic resonance imaging,rsfMRI)数据来表达,该表达称为功能连接.已有研究表明,精神障碍疾病与患者脑区之间功能连接的异常改变密切相关[1].因此,对脑功能连接分类的研究有助于揭示脑疾病的致病原因,具有十分重要的现实意义.

目前脑功能连接分类方法主要分为两种:基于传统机器学习的分类方法和基于深度学习的分类方法.基于传统机器学习的分类方法使用浅层模型分析脑功能连接,其中支持向量机(Support vector machine,SVM)[2-3]和套索算法(Least absolute shrinkage and selection operator,LASSO)是两种最常用的算法.虽然传统的机器学习方法已经表现出较好的分类效果,但是受限于浅层结构,特征表达能力不足,分类准确率有待进一步提升.与传统机器学习方法相比,深度学习方法具有更强的特征提取能力,能够系统地从脑功能连接中提取从低层次到高层次的特征.其中,栈式自编码器(Stacked autoencoders,SAE)结构简单,能够逐层提取数据中深层次的特征,是脑功能连接分类任务中最常用的深度学习方法之一[4-5].此外,有研究将卷积神经网络(Convolutional neural network,CNN)应用于脑功能连接分类任务,针对脑功能连接的特点设计了多种网络结构,取得了不错的效果[6-7].不过,基于深度学习的脑功能连接分类准确率仍存在进一步的提升空间.

近年来,有研究发现,在分类时综合利用深度模型提取的不同层次的特征,相比于仅使用最高层次的特征能够提升分类效果.Sun 等[8]使用CNN来提取人脸特征,将其用于人脸分类任务.该方法将CNN 中最后一个池化层与全连接层提取的特征拼接起来,作为最终的特征表示,在分类时充分考虑了不同层次特征中的信息,与一些代表性的方法相比具有较高的分类准确率.张婷等[9]在传统CNN的基础上引入了跨层连接思想,将CNN 中第二个池化层的特征跨越模型中间的隐层直接与全连接层连接起来,最后使用该特征来预测样本类别.该方法可以有效地将高层次特征和低层次特征结合起来,在人脸性别分类任务中获得了比传统CNN更高的准确率.李勇等[10]针对LeNet-5 在表情识别中识别率不高的问题提出了一种基于跨连接LeNet-5 网络的面部表情识别方法,该方法能够将神经网络提取的低层次特征和高层次特征融合,提高了表情识别率.最近,又有研究表明,将原型学习与深度学习结合能够提取到类内差异小,类间差异大的鉴别性特征.Yang 等[11]将原型学习与CNN 结合,提出了卷积原型学习,该模型能够显著缩小CNN 提取到的特征的类内差异,提高了CNN 的鲁棒性.Wang 等[12]提出了一种基于原型学习的原型集成方法,该方法不仅能够缩小深度特征的类内差异,而且能够扩大类间差异,从而提高了增量学习中新类别的检测的鲁棒性.Zhang 等[13]提出了模态缺失情况下的深度编码及分类模型(Cross partial multiview networks,CPM-Nets),该模型充分利用完备信息编码和原型分类思想,提高了模态缺失情况下多模态数据的分类性能.可见,将原型学习与深度学习结合用于脑功能连接分类任务,并且在分类阶段综合利用深度模型提取到的不同层次的特征,将有望在获得与疾病相关的鉴别性特征的同时进一步提升分类准确率.

为了进一步提高脑功能连接的分类效果,本文提出基于原型学习与深度特征融合的脑功能连接分类方法.与CPM-Nets 不同的是,本文使用的数据为单一模态,并不涉及模态缺失的情况;此外本文所提方法还探索了深度模型中不同层次的特征对分类性能的影响.具体来说,首先,利用SAE 提取脑功能连接中不同层次的特征;然后,使用原型学习在SAE 的每个隐层中提取表示样本类别信息的距离特征;最后,利用提出的深度特征融合策略将提取到的距离特征融合,并将该融合特征用于类别标签预测.在ABIDE 数据集上的实验结果表明,本文所提方法不仅提升了脑功能连接的分类准确率,而且能够根据模型提取到的鉴别性特征更加准确地定位与精神障碍疾病相关的脑区.

1 相关工作

1.1 脑功能连接分类

脑功能连接分类是一种通过分析脑功能连接来判断被试是否患有精神疾病的技术,近年来得到了广泛研究.Craddock 等[2]首次使用RFE-SVM 来对抑郁症患者的脑功能连接分类,该方法首先使用递归式特征消除(Recursive feature elimination,RFE)算法选择功能连接中对分类贡献较大的特征,然后利用这些特征训练SVM,能够有效地区分正常对照(Typical controls,TC)和抑郁症患者,目前已广泛应用于脑功能连接分类任务.Khazaee 等[3]利用图论构建脑功能连接,经过特征选择后使用SVM作为分类器进行分类,可以有效地识别出轻度认知障碍(Mild cognitive impairment,MCI)和阿尔兹海默症(Alzheimer＇s disease,AD).Wang 等[14]将SVM 用于青少年精神分裂症(Schizophrenia,SZ)患者与TC 的脑功能连接分类任务,并通过学习到的权值识别出了与疾病相关的异常脑区.Bi 等[15]指出单个SVM 容易受到核函数,惩罚系数等因素的影响,因此提出了一种基于随机SVM 的脑功能连接分类方法.该方法从训练集中随机选取部分样本,经过特征提取后用来训练一个SVM 分类器,多次重复上述过程得到多个SVM 分类器,在测试时使用投票策略来预测样本类别.此外,由于LASSO能够获得稀疏的特征表示,在脑功能连接的分类中的应用也较为广泛.Watanabe 等[16]针对功能连接的结构信息提出了一种正则化框架,使用LASSO对功能连接进行稀疏性约束,将稀疏化的功能连接特征作为SVM 的输入来分类,提高了脑功能连接的分类效果.然而,这些浅层模型无法提取数据中深层次的特征,给算法的性能带来了限制.

近年来,深度学习方法常被用来提取数据深层次的特征,提高了脑功能连接的分类准确率.Kim等[4]认为使用深度学习方法在功能连接中提取的高层次特征能够提高分类效果,提出了一种带有权重稀疏控制的SAE,通过L1正则化控制每个隐层权重的稀疏性.在精神分裂症的分类任务中,误差明显低于SVM,此外,通过定量地分析各隐层的权重发现,从高隐层中提取的特征表现出了SZ 组与TC 组之间脑功能连接整体性的差异.Li 等[5]提出了一种用于脑功能连接分类的迁移学习框架,首先使用SAE 学习TC 组的功能连接模式,然后将该模型用于自闭症谱系障碍(Autism spectrum disorder,ASD)的分类任务,提高了神经网络在小数据集中的泛化能力.Anibal 等[17]使用含有两个隐层的栈式去噪自编码器(Stacked denoising autoencoders,SDAE)提取脑功能连接中低维度的特征,对1 035名被试(其中包含505 名ASD和530名TC)进行了分类,准确率达到了70 %.Ju 等[18]构建了一个用来分类正常衰老和轻度认知障碍的SAE,相比于传统机器学习方法,分类精度提高了31.32 %.除了SAE,基于CNN 的方法在脑功能连接分类中同样应用广泛.Parisot 等[19]提出了一种图卷积神经网络(Graph convolution network,GCN)分类框架,他们将所有被试表示为一个稀疏的图,图的节点为脑功能连接,边的权重通过性别,年龄等表型信息确定.该方法通过图模型将脑功能连接与表型数据结合,取得了不错的分类效果.Meszlényi 等[6]针对功能连接的特点,利用CNN 的多通道机制提出了Connectome-CNN (CCNN)模型,该模型能够系统地整合功能连接中不同维度的特征,提高了分类准确率.Kawahara 等[7]提出了基于CNN 的Brain-NetCNN 框架,设计了边到边层,边到节点层,节点到图层三种不同的卷积层来提取脑功能连接不同层次的拓扑特征.Brown 等[20]进一步扩展了Brain-NetCNN 框架,利用数据驱动的大脑解剖结构特性来对脑功能连接进行正则化.该方法不仅提高了分类准确率,还能根据学习到的网络参数来分析对分类贡献较大的特征.Xing 等[21]考虑到不同脑区对应的功能连接之间的独立性,基于BrainNetCNN框架提出了一种带有独立卷积核的CNN.该模型赋予每条功能连接独一无二的权重,更加真实地反映了脑功能连接中的拓扑结构信息,因此能够更加精确地识别异常脑区.可见,基于深度学习的脑功能连接分类方法已成为一个前沿热点.

1.2 原型学习

原型学习是模式识别领域中一种经典的学习方法,主要思想是从数据中学习能够很好地表示各类特征分布的原型,然后根据特征到原型的距离来分类.其中最著名的是K 最邻近分类算法(K-nearestneighbor,KNN).为了提高KNN 的计算效率,Kohonen[22]提出了学习矢量量化(Learning vector quantization,LVQ),由于其结构简单,学习能力强,之后衍生出了许多改进版本,如LVQ2,LVQ3[23].按照原型更新的方式可以将原型学习分为两大类:一类是通过人工设计的更新规则来更新原型,另一类是使用自定义损失函数,通过参数优化的方式来更新原型.其中基于参数优化的学习方法由于灵活性高,应用更为广泛.然而这些经典的原型学习方法使用的是基于手工设计的浅层特征,给算法的性能带来了限制.

最近,有研究尝试将原型学习与深度学习结合,明显提升了模型的分类准确率和鲁棒性.Snell 等[24]提出了一种原型网络,它能够学习一个度量空间,在这个空间中通过计算特征到每个类的原型的距离来分类.该方法在小样本学习领域取得了不错的效果.Boney 等[25]进一步改进了原型网络,通过添加自适应策略来识别新的类别,并将其应用于半监督模式下的小样本学习.Yang 等[11]将原型学习与卷积神经网络结合,提出了卷积原型学习,该模型在每个类别中学习多个原型,然后通过度量特征与原型的距离来进行类别预测.实验表明,相比于传统的CNN,该模型不仅在增量学习上有巨大优势,而且能够获得类内差异小,类间差异大的鉴别性特征.Wang 等[12]提出了一种原型集成的方法,用于增量学习中新类别的检测,该方法能够缩小CNN 提取到的特征的类内差异,扩大类间差异,从而提高了新类别的检测的鲁棒性.Zhang 等[13]假设不同模态的信息能够由一个公共特征来表示,将多个模态的数据通过深度编码映射为一个公共特征,然后使用非参数化分类器对该特征进行分类.该方法避免了参数化的分类器带来的泛化能力下降的问题,并且分类结果具有较高的可解释性,本质上是多模态原型分类.因此,原型学习能够进一步提升深度学习模型的特征提取能力,从而提升分类效果.

2 基于原型学习与深度特征融合的脑功能连接分类方法

2.1 基本思想和框架

原型学习使用特征空间中的一组原型来表示某个类别中特征的分布中心,通过度量特征到原型的距离来进行类别标签预测.因此,我们将原型学习与SAE 结合,通过度量由SAE 提取的脑功能连接特征到原型的距离来表示功能连接所属的类别,并且训练过程中不断减小特征到同类别原型的距离,扩大特征到不同类别原型的距离,从而提升SAE提取鉴别性特征的能力.

SAE 能够通过一系列非线性变换从脑功能连接中提取从低层次到高层次的特征,其中低层次特征表达脑功能连接的局部信息,高层次特征表达脑功能连接的全局信息,在分类时综合利用各层次特征有望进一步提升分类准确率.为此,本文提出深度特征融合策略,目的是在分类时充分利用不同层次的特征中,以此来提升模型的分类准确率.

基于上述思想,本文提出了基于原型学习与深度特征融合的脑功能连接分类方法,整体框架如图1所示.该分类模型主要由两部分构成:第一部分如实线框(1)所示,为自编码器的无监督预训练;第二部分如实线框(2)所示,为整个模型的有监督微调.其中第二部分包含三个关键步骤:虚线框(b)所示的基于栈式自编码器的逐层特征提取,用于提取脑功能连接中不同层次的特征;虚线框(c)所示的基于原型学习的距离特征提取,通过距离来表示抽象特征的类别信息;虚线框(d)所示的深度特征融合策略,该策略的目的是将各隐层的距离特征进行融合.最后使用融合后的特征来预测脑功能连接的类别标签.

2.2 基于栈式自编码器的逐层特征提取

为了提取脑功能连接中不同层次的特征,我们构建了一个具有L个隐层的SAE.自编码器是一个单隐层的全连接神经网络,通过重构输入来获得隐层的特征表示.如图1 (a)所示,无监督预训练L个自编码器,训练完成后按图1 (b)将这些自编码器堆叠起来,构成一个具有L个隐层的SAE,使用这个SAE 来提取脑功能连接不同层次的特征.

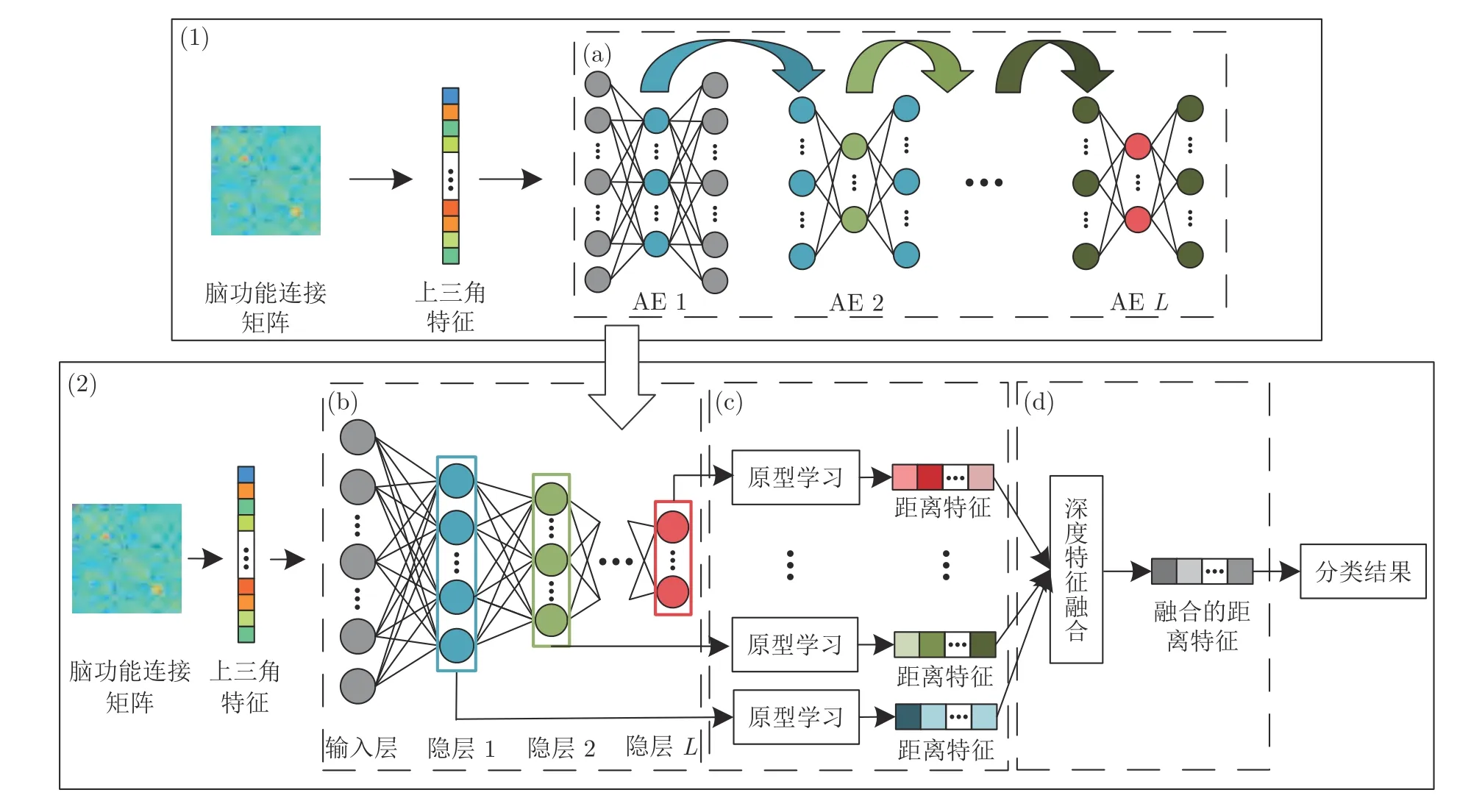
图1 基于原型学习与深度特征融合的脑功能连接分类方法结构图Fig.1 Architecture of brain functional connection classification based on prototype learning and deep feature fusion

在训练第一个自编码器时,将脑功能连接x ∈Rn×1作为输入,n为特征维度,首先通过编码器得到x的隐层特征,再由解码器对该特征进行重构,通过最小化输入与输出之间的误差来优化网络参数.隐层特征的计算公式为:

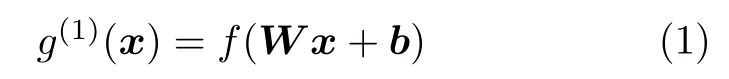
其中g(1)(x) 表示第一个自编码器提取到的隐层特征,f(·) 为非线性激活函数,W和b分别表示编码器的权值和偏置.重构输出为:

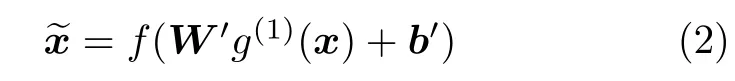
其中W′和b′分别表示解码器的权值和偏置.训练阶段的损失函数为:

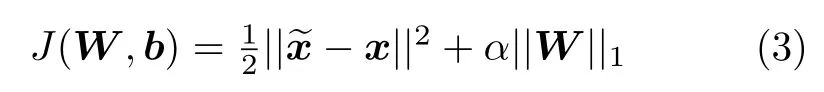
上式第一部分为均方误差,表示输入与重构输出之间的差异,第二项为L1正则化项,目的是得到脑功能连接稀疏的隐层特征表示,α为正则化项的系数.

当第一个自编码器训练完成后,将其隐层特征作为输入来训练第二个自编码器,直到L个自编码器全部训练完成,然后将它们的编码器部分堆叠起来构建一个具有L个隐层的SAE.我们将SAE 作为特征提取器,第l个隐层提取到的特征记为g(l)(x),其中l∈{1,2,···,L}.当l较小时提取到是表达局部信息的低层次特征,当l较大时提取到的是表达全局信息的高层次特征.

2.3 基于原型学习的距离特征提取

在本节中,我们在SAE 的每个隐层中,利用原型学习提取能够表示脑功能连接类别信息的距离特征.距离特征是一个向量,其维数与数据类别的数量相同,各元素为隐层特征到对应类别中所有原型的最小距离.接下来介绍提取过程.

在第L个隐层中,首先使用在训练集中提取的特征的平均值来初始化对应类别的原型,记为,其中c∈{1,2,···,C},C为类别数量,j ∈{1,2,···,K}表示第j个原型,K为每个类别中原型的数量.然后计算隐层特征到所有原型的欧氏距离,将各类别中距离的最小值表示为,计算公式如下:

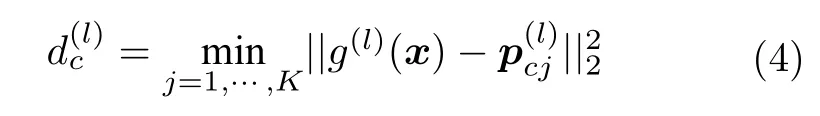
最后将计算得到的隐层特征到各类别原型的最小距离组成一个向量,该向量即为距离特征.由于原型可以看作特征分布的中心,那么和原型类别相同的特征将会与原型之间具有较小的距离,和原型类别不同的特征与原型之间的距离会相对较大,所以越小,表示g(l)(x) 与的相似度越大,属于同一类别的概率越大.因此,距离特征可以用来计算脑功能连接所属类别的概率.

图2 为在SAE 的第l个隐层空间中使用原型学习进行距离特征提取的示意图,其中类别数量C=2,每个类中的原型数量K=2,可以看到隐层特征到类别标签为1 的原型的最小距离为1.3,到类别标签为2 的原型的最小距离为2.0,因此第l层中提取的距离特征D(l)=[1.3,2.0] .

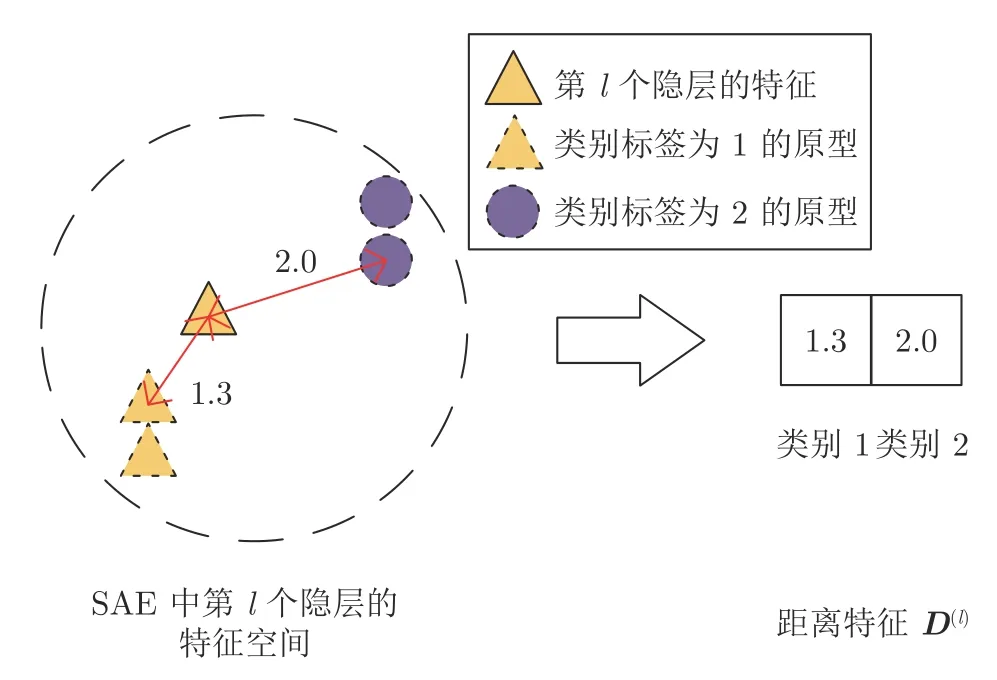
图2 基于原型学习的距离特征提取示意图Fig.2 Illustration of the distance feature extraction based on prototype learning

2.4 深度特征融合

在SAE 的多层结构中,从不同隐层中提取到的特征表达的信息不尽相同,其中从低隐层中提取的一般为表示脑功能连接局部信息的低层次特征,而从较高隐层中提取的是表示脑功能连接全局信息的高层次特征.为了在分类时综合利用高层次和低层次特征中的类别信息,本文提出深度特征融合策略.该策略通过逐元素相加的方法将多个隐层中基于原型学习提取的距离特征融合,使用融合后的特征来预测脑功能连接的类别,充分利用了高层次特征和低层次特征中的类别信息,实现了信息互补,有利于提升分类准确率.下面介绍深度特征融合的具体实现过程.

首先使用上一节中介绍的方法在SAE 的每个隐层中提取一个距离特征,由于从不同的隐层中提取的特征所表达的信息有所差别,所以不同隐层中的距离特征所表示的类别信息也会有所差异;然后对所有距离特征进行归一化操作,目的是消除数量级的差异,由于不同隐层神经元数量有所差异,所以从不同隐层提取的距离特征的数量级也会不同,如果直接将距离特征融合,会造成很大的偏差;接着为每个隐层赋予一个权重系数,将其与归一化的距离特征相乘,该权重系数决定隐层特征对最终分类结果的贡献程度,其值越大,表示对应隐层特征对分类结果的影响越大;最后将所有归一化与加权后的距离特征逐元素相加,即为融合后的距离特征.具体计算公式如下:

其中D=[d1,d2,···,dC] 表示融合后的距离特征.β(l) 表示第l层的权重系数,通过验证集在各隐层的准确率的比值来确定,既考虑了不同隐层对最终分类结果的影响,又避免了人为设置带来的偏差,并且.此外,当指定β(l)=0 时,表示第l层的距离特征不参与融合,因此可以灵活地控制特征的融合方式.h(·) 为归一化函数.

2.5 分类模型

在本文中,我们使用融合后的距离特征来预测功能连接的类别,相当于综合考虑了各隐层特征对分类的贡献.因此,x属于类别y的概率可以表示为:

其中γ为控制概率赋值的超参数,由于特征到原型的距离越近,属于同一类别的概率越大,因此需要取反.

我们的目标是学习一个能够提取鉴别性特征并且具有较高分类准确率的深度神经网络,因此,设计合适的损失函数至关重要.基于上式,我们可以使用基于距离的交叉熵损失(Distance based cross entropy loss,DCE loss)来计算分类误差,公式如下:

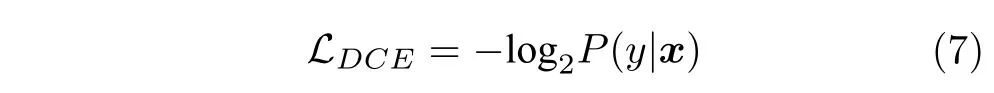
最小化DCE loss 相当于减小各隐层特征到对应原型的距离,所以能够学习到类内差异较小的特征.然而,训练过程中仅靠DCE loss 有过拟合的风险.因此,我们在损失函数中加入了基于间隔的原型损失(Margin based prototype loss,MP loss)作为正则化项,在训练过程中减小各隐层特征到对应类别原型之间距离的同时,扩大到不同类别原型之间的距离.假设从脑功能连接x提取的融合距离特征中,dy和dr分别表示到相同类别原型的距离和到不同类别原型的最小距离,那么当样本分类正确时,有dy＜dr,此时我们认为正则化项应该为零;当样本分类错误时,有dy＞dr,这种情况下我们认为正则化项应该大于零.为了进一步地提升模型的泛化能力,我们在损失函数中加入间隔超参数,因此基于间隔的原型损失定义为:

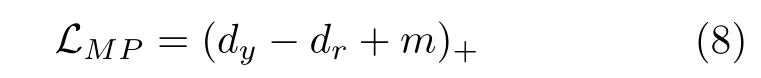
其中m∈(0,1) 为间隔超参数.即使样本分类正确,也会对模型施加惩罚,从而提高模型的泛化能力.由于原型是可训练的,所以最小化MP loss 意味着缩小特征到同类别原型间的距离,扩大到不同类别原型之间的距离.那么在SAE 的各隐层中,不同类别的隐层特征将具有更大的类间差异.最后,将DCE loss和MP loss 联合起来训练SAE,整体损失函数为:

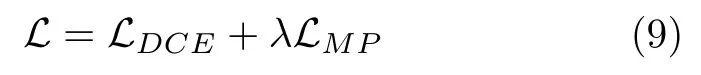
其中,λ是正则化项的系数.

2.6 算法描述

基于原型学习与深度特征融合的脑功能连接分类方法的训练过程如算法1 所示.

算法1.基于原型学习与深度特征融合的脑功能连接分类方法

Output:SAE 的网络参数和所有原型.

算法1 通过无监督预训练的方式初始化SAE的网络参数,能够使各隐层中的原型在初始化时就具有较好的代表性.在训练模型时,使用的是有监督的方法,在缩小特征到同类别原型之间距离的同时,扩大到不同类别原型之间的距离,因此能够提取到类内差异小,类间差异大的鉴别性特征.

3 实验结果与分析

3.1 实验数据与预处理

本研究使用ABIDE 数据集来验证所提方法的有效性.该数据集共享来自世界各地的自闭症脑影像数据,旨在通过大规模数据加快对自闭症神经基础的理解.其中包含来自17 个不同站点的1 112 名被试的rs-fMRI 数据.由于77 名被试的数据异常,经筛选后,使用剩余1 035 名被试的脑功能连接作为实验数据,其中TC 组530 人,ASD 组505 人.

预处理过程如下.首先,本文采用Preprocessed connectomes project (PCP)提供的Configurable pipeline for the analysis of connectomes(CPAC)预处理流程,包括层间时间校正,头动校正,全局平均强度归一化,干扰信号回归,带通滤波和空间配准等.然后,使用Craddock 等[26]提出的CC200 模板来识别大脑皮层中的感兴趣区域(Region of interest,ROI).该模板将大脑皮层划分为200 个空间相近,功能活动相关的区域.从预处理的rs-fMRI 中提取各个ROI 的平均时间序列.接着,利用各个ROI 的平均时间序列计算每对ROI之间的皮尔逊相关系数(Pearson correlation coefficient,PCC),通过Fisher＇s z 变换将得到的相关系数归一化,得到每个被试的功能连接矩阵,大小为200×200,其中每个元素表示一对ROI 之间的连接强度.最后,选取功能连接矩阵的上三角,将其展开为一维向量作为模型的输入,该一维向量的维数计算公式如下:

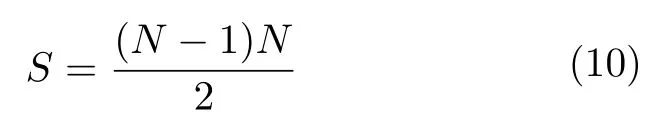
其中N为ROI 的数量,S为一维向量的维数,本研究中N=200,因此S=19 900 .

3.2 实验设置和评价指标

在大多数文献中,SAE 的隐层节点数量通常是根据经验设置的.如果隐层节点数量太多,会增加训练时间,如果数量太少,可能无法充分提取有价值的特征,出现欠拟合的现象.在本文中,我们将第一个隐层的节点数量设置为1 000,其余隐层节点数量设置为100,实验中所有SAE 均按此设置构建.训练时使用Adam 梯度下降算法最小化损失函数,每次迭代的批大小为96,更新参数时学习率的大小为 1×10-4.所有实验的训练集,验证集,测试集的划分比例为3:1:1,并根据该划分循环,使得每一折都作为测试数据对实验性能进行评估.上述过程重复运行十次后取实验结果的平均值来验证所提方法的有效性.

实验采用目前广泛使用的准确率(Accuracy,ACC),灵敏度(Sensitivity,SEN),特异度(Specificity,SPE),正预测率(Positive predictive value,PPV)和负预测率(Negative predictive value,NPV)五种指标评价模型的分类性能.五种指标的计算公式如下:

其中,TP表示实际标签为正,预测标签为正的样本数量;TN表示实际标签为负,预测标签为负的样本数量;FP表示实际标签为负,预测标签为正的样本数量;FN表示实际标签为正,预测标签为负的样本数量.

3.3 不同实验策略对分类性能的影响

3.3.1 隐层数量对分类性能的影响

在本节,为了确定结合原型学习的SAE (SAEPL)中的隐层数量L,我们构建了多个具有不同隐层数量的SAE-PL,为了便于比较,我们在最后一个隐层中固定每个类别中的原型数量K=1,使用本文提出的损失函数训练模型,除隐层数量外,其余超参数设置相同.表1 给出了不同隐层数量下SAE-PL 的实验结果.

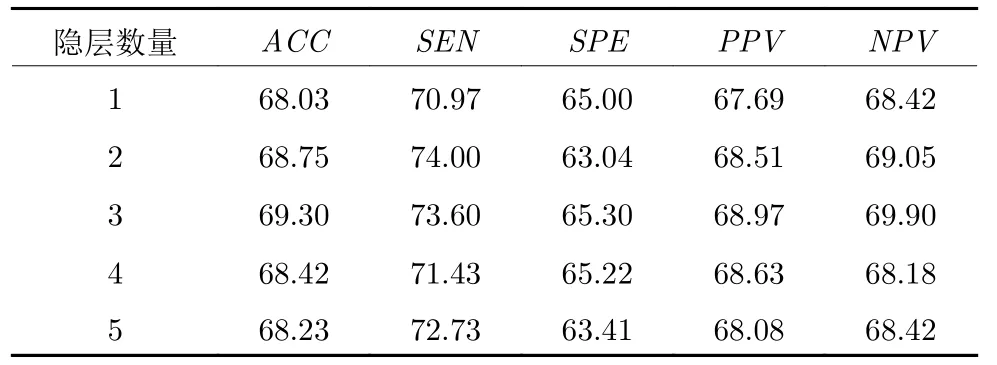
表1 不同隐层数量下的实验结果(%)Table 1 Experimental results of our method with different hidden layers (%)

从表1 中可以看到,当L=1 时,分类准确率最低,原因是隐层数量太少,无法充分提取脑功能连接中的深层次特征.随着隐层数量增加,分类准确率逐渐上升,当L=3 时分类准确率最高,达到了69.30 %,并且在SPE,PPV,NPV三个指标上均达到了最高值.而随着隐层数量继续增加,出现了分类性能下降的现象,其原因是脑功能连接的数据量较少,当网络结构复杂时,会出现过拟合的现象,从而影响分类效果.因此,在后续实验中我们选择具有3 个隐层的SAE-PL 作为基本结构.

3.3.2 原型数量对分类性能的影响

在本节中,我们使用上一节中确定的网络结构,在SAE-PL 的最后一个隐层中利用原型学习分别在ASD 组和TC 组中学习一组代表性的原型.为了测试SAE-PL 中原型数量K对实验结果的影响,我们分别取不同的K值进行了实验.除了原型数量外,其余超参数设置相同,结果如表2 所示.

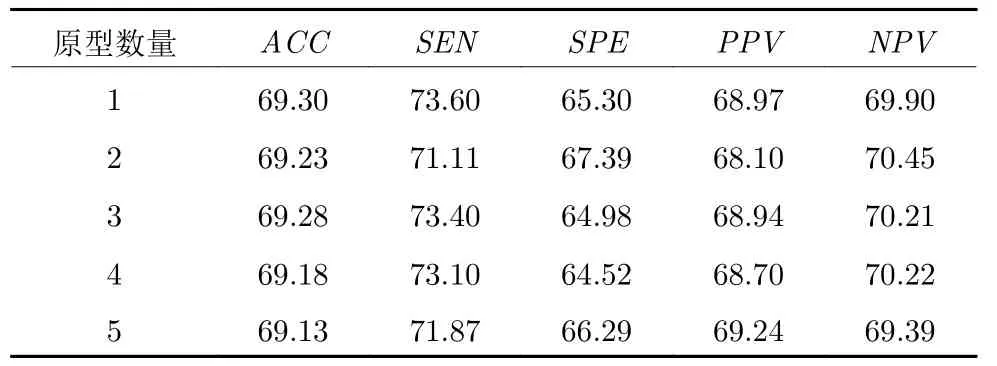
表2 不同原型数量下的实验结果(%)Table 2 Experimental results of our method with different number of prototypes (%)

从表中可以看到,K=1 时取得了最高的ACC和SEN.对于不同的K值,实验结果差异并不明显,在每个类别中设置多个原型并没有带来分类准确率的提升.其主要原因是SAE-PL 具有强大的特征提取能力,在每个类别中使用单个原型就能够较好地表示特征的分布,所以引入多个原型并不会提高分类性能.而当数据的类内分布较为复杂时,使用多个原型可能会得到更好的结果.因此,在后续实验中使用的原型数量K均为1.

3.4 原型学习对特征分布的影响

为了探究原型学习对特征分布的影响,我们还基于最常用的softmax 损失函数训练了一个没有结合原型学习的传统SAE,然后利用Wen 等[27]提出的toy model 分别将SAE和SAE-PL 中最后一个隐层提取到的特征投影到二维空间中,对其进行可视化,结果如图3 所示.图3 (a)是本文所提方法提取到的特征的分布情况,图3 (b)为传统SAE 提取到的特征分布情况.从图中可以看出,传统SAE 提取的特征类内差异较大,类间差异较小,而SAEPL 提取到的特征类内差异明显更小,类间差异更大,因此SAE-PL 能够提取到具有鉴别性的特征.

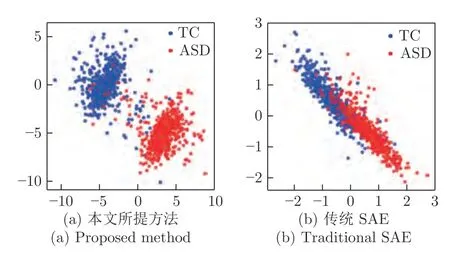
图3 两种方法的特征分布对比Fig.3 Comparison of the two methods＇feature distribution

此外,我们还进一步探索了根据SAE和SAEPL 提取到的特征识别出的异常脑区的差异.具体地,使用Simonyan 等[28]提出的特征排序方法定义一个类评分函数:

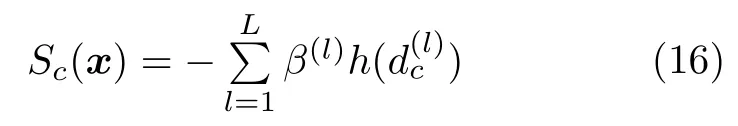
给定一个功能连接数据xi和其类别,使用向量wi表示xi中各元素的重要程度,wi的计算方式为:

模型训练完成后固定网络参数,由式(17)根据链式求导法则计算测试集中每个功能连接对分类贡献的权值,权值的绝对值越大表示对分类结果的贡献越高.然后将测试集中所有数据计算得到的权值的绝对值相加,得到每个功能连接最终的分类贡献.最后按取前十个贡献最大的连接,这些连接对应的脑区即为与疾病相关的异常脑区.图4 分别展示了由两种方法提取的特征分析得到的前10 个重要连接,每条线的粗细表示对分类任务的贡献程度,较粗的线表示贡献较大.值得注意的是,由SAE-PL提取的特征分析得到的梭状回(FFG),丘脑(THA),海马(HIP)等异常脑区在其他研究[6,17]中被证实与ASD 相关,而通过SAE 得到的异常脑区中却没有涉及.因此,SAE-PL 提取的鉴别性特征能够更加准确地定位与疾病相关的异常脑区.

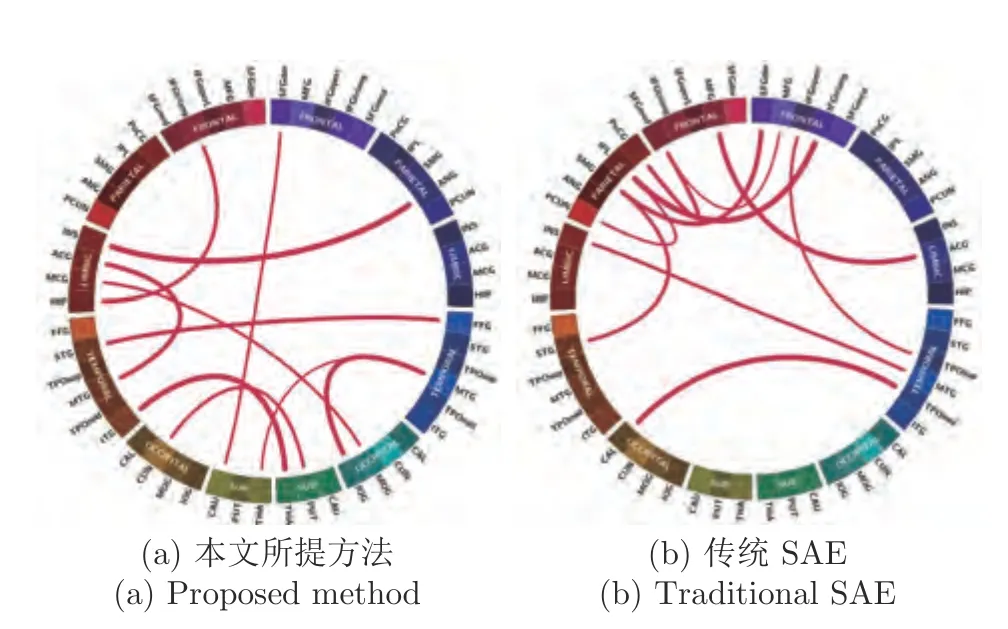
图4 两种方法得到的前十个重要连接Fig.4 Top ten important connections learned by two methods

3.5 深度特征融合对分类性能的影响

本节测试了深度特征融合策略对实验结果的影响.我们使用式(5)将SAE-PL 的不同隐层中由原型学习提取的距离特征融合.通过将第l层的加权系数置零来控制特征融合的方式,最后使用融合后的特征来分类.其中DFF-3 对应的β(1)=0,β(2)=0,表示仅使用最后一个隐层中的距离特征分类,DFF-1,3 对应的β(2)=0,表示融合第一层和第三层中的距离特征,DFF-2,3 对应的β(1)=0,表示融合第二层和第三层中的距离特征,DFF-all 表示融合所有隐层中的距离特征.实验结果如表3 所示.

由表3 可以看出,DFF-3 的ACC最低,这是因为在分类时仅使用了高层次的特征,没有充分利用SAE 提取到的各层次的特征.而DFF-1,3和DFF-2,3 融合了低隐层中的距离特征,ACC和其他各项指标均有所提升.DFF-all (下文记为SAE-PLDFF) 在分类时使用融合全部隐层中的距离特征ACC指标达到了最高的70.30 %,并且在SPE,PPV和NPV三个指标上均取得了最高值,说明综合考虑高层次特征和低层次特征有利于提升分类性能,有效的验证了深度特征融合的有效性.

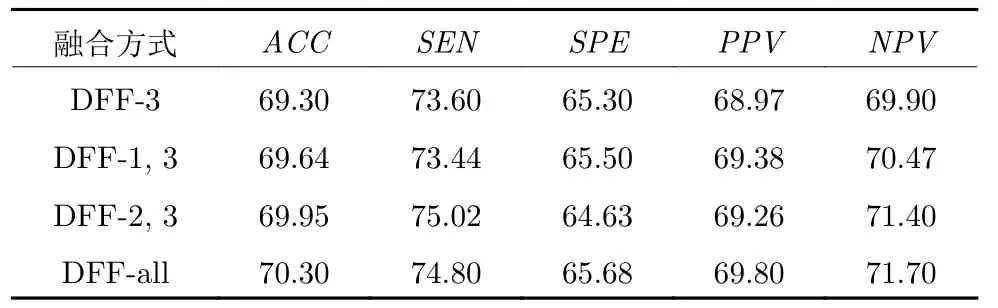
表3 不同深度特征融合方式下的实验结果(%)Table 3 Experimental results of our method with different deep feature fusion modes (%)

3.6 算法的收敛性

为了直观地展示本文所提算法的收敛性,我们绘制了无监督预训练和有监督微调两个阶段的Loss 曲线,如图5 所示.

在预训练阶段,由图5 (a),(b),(c) 所示的Loss 曲线可以看出,整体的收敛效果较好,当验证集Loss 最低时,保存网络参数用于后续的训练;在微调阶段,训练集的Loss 虽略有抖动,但整体呈下降趋势,验证集和测试集的Loss 也随迭代次数的增加整体下降,最终保存验证集Loss 最低时的网络参数用于测试.综上,算法1 是收敛的.

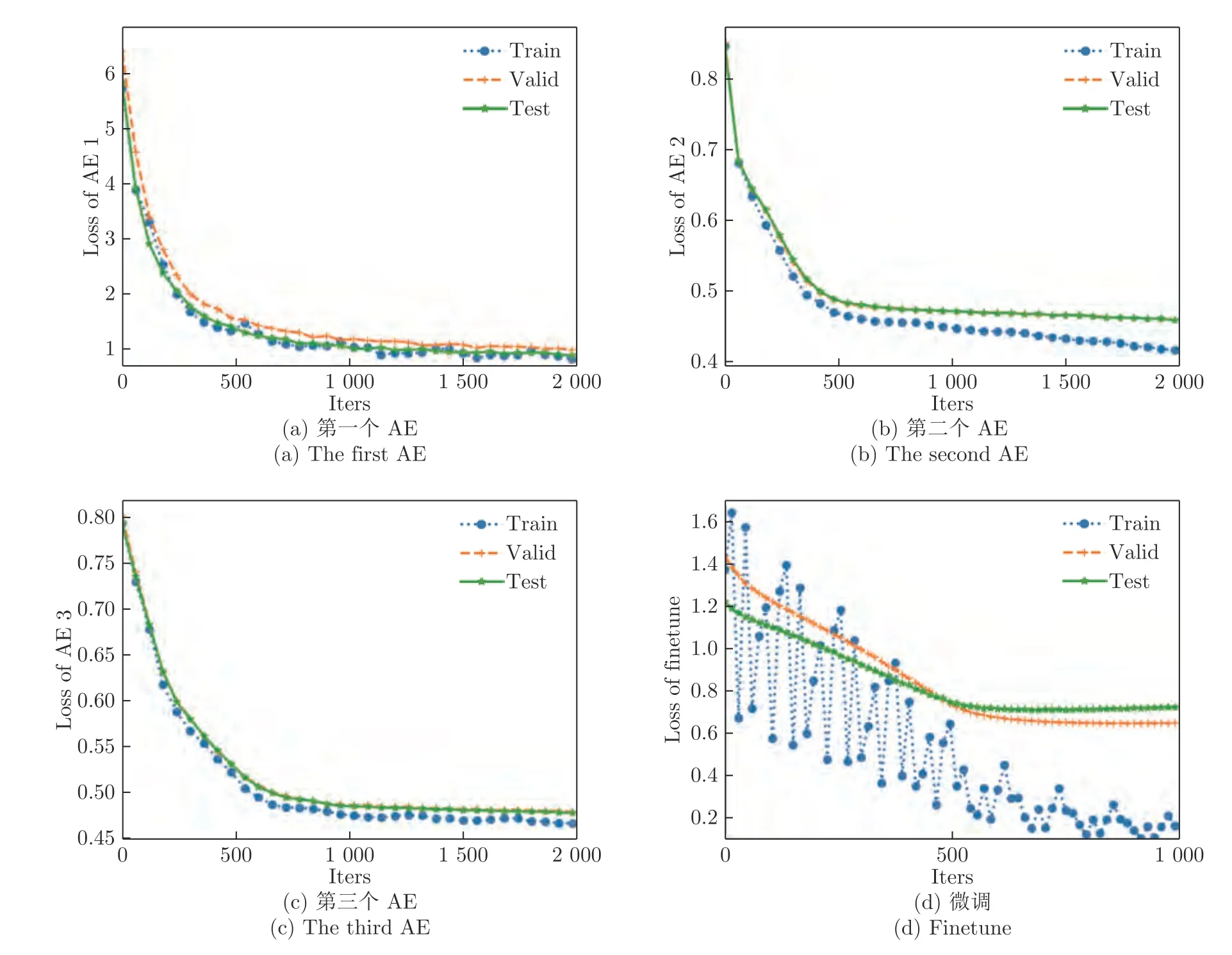
图5 算法1 的训练曲线Fig.5 Train plot of the algorithm 1

3.7 与多种经典算法的对比实验

为了验证本文所提方法相比于其他方法的优劣,我们分别从传统的机器学习方法和深度学习方法中选取了六种经典算法进行对比实验.其中基于传统机器学习的方法包括RFE-SVM[2]和LASSO[29],基于深度学习的方法包括BrainNetCNN[7],CCNN[6],SDAE[17]和GCN[19].结果如图6 所示.

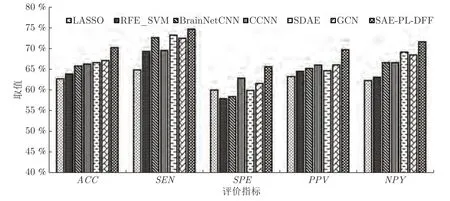
图6 七种方法的分类性能对比Fig.6 Performance comparison of the seven methods

从图中的实验结果可以看出,本文所提方法SAE-PL-DFF 在各项指标上均达到最优,分类效果明显优于其他算法.在这七种方法中,基于深度学习的方法明显优于基于传统机器学习的方法.基于传统机器学习的算法ACC指标均低于65 %,这是由于传统机器学习模型为浅层模型,无法充分挖掘脑功能连接中有价值的深层信息,而基于深度学习的方法ACC指标均在65 %以上,体现了深度学习方法处理高维的脑功能连接上的优势.对比其他4种基于深度学习的方法,SAE-PL-DFF 明显优于BrainNetCNN,CCNN,GCN和SDAE (p＜0.05),ACC指标达到了70.3 %,其余各项指标的优势也相当明显,其原因主要在于两个方面:1)原型学习能够辅助SAE 提取到类内差异小,类间差异大的鉴别性特征,提高了模型的判别能力;2)本文所提方法融合了深度模型提取的低层次特征和高层次特征,实现了脑功能连接局部信息和全局信息的互补,进一步提升了分类准确率.上述结果验证了本文所提方法的有效性.

4 结论

本文提出了一种基于原型学习与深度特征融合的脑功能连接分类方法.该方法使用栈式自编码器提取脑功能连接中从低层次到高层次的特征,然后利用原型学习提取表示类别信息的距离特征,最后利用提出的深度特征融合策略将这些距离特征融合,使用融合后的特征来对脑功能连接分类.相关实验表明,所提方法能够有效地提取并利用不同层次的鉴别性特征,进一步提升了脑功能连接的分类准确率.值得一提的是,尽管我们只在脑功能连接数据上进行了实验,但是所提方法是通用的,也可以应用于其他分类任务.

下一步的工作将进一步扩展本文所提方法,使用不同类型的模板来构建不同视角的脑功能连接,将多视角深度学习方法用于脑功能连接分类,试图综合利用多个视角中的有效信息,进一步提升脑功能连接的分类效果.