时间分数阶扩散波方程的无单元Galerkin法分析*
吴 迪, 李小林
(重庆师范大学 数学科学学院,重庆 401331)
引 言
时间分数阶扩散波方程可以用来模拟一些重要的物理现象[1-2],比如黏弹性介质中机械波的传播、具有记忆的非Markov 扩散过程、以及非晶态半导体中的电荷运输.有限差分法[1-5]和有限元法[5-8]等方法在近年来被用于数值求解此方程.
无网格法基于点的近似,摆脱了有限差分和有限元等方法中网格单元的限制,具有实施便利和精度高等优势[9].Yang 等[10]和Kumar 等[11]发展了数值求解时间分数阶扩散波方程的无网格配点法.无单元Galerkin法[8,12-13]是一种基于移动最小二乘近似的全局弱式无网格法,比无网格配点法具有更好的稳定性.Dehghan 和Abbaszadeh 通过使用L1 逼近公式离散时间变量,在文献[14]中建立了数值求解时间分数阶扩散波方程的无单元Galerkin 法,但是只处理了Neumann 边界条件,没有包含无单元Galerkin 法不易处理的Dirichlet 边界条件.他们在文献[8]和[15]中用插值型无单元Galerkin 法,数值求解了含有Dirichlet 边界条件的时间分数阶扩散波方程,但是在构造形函数时需要使用特殊的奇异权函数.
本文研究了Caputo 意义下的时间分数阶扩散波方程的无单元Galerkin 法.首先,类似于文献[8,14-15],基于文献[1]中的L1 逼近公式,离散时间变量.其次,为了有效处理Dirichlet 边界条件并避免使用奇异权函数,本文通过罚函数方法处理Dirichlet 边界条件,建立了该方程的无单元Galerkin 法离散线性代数方程组.然后,借鉴文献[16-17]的技巧理论分析了时间分数阶扩散波方程的无单元Galerkin 法的误差.最后,利用数值算例,进一步论证了该方法的有效性和精度.
1 问题描述
考虑如下时间分数阶扩散波方程[1]:
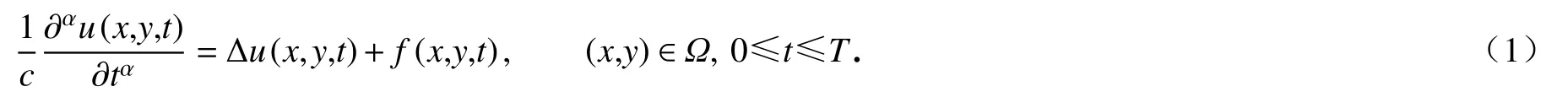
初始条件为
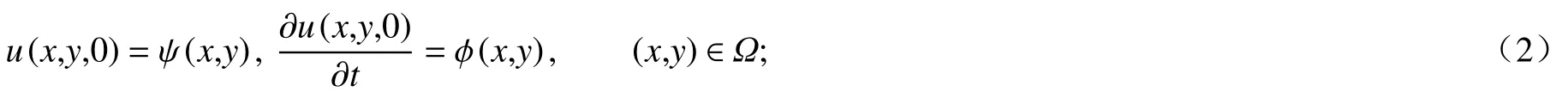
边界条件为

其中c为扩散波动系数, Δu=∂2u/∂x2+∂2u/∂y2, Ω 是问题区域, Γ1是 Dirichlet 边界, Γ2是 Neumann 边界,n是边界∂Ω=Γ1∪Γ2上 的外法向单位向量,f(x,y), ψ (x,y) ,φ (x,y), ξ (x,y), γ (x,y)是已知函数,且
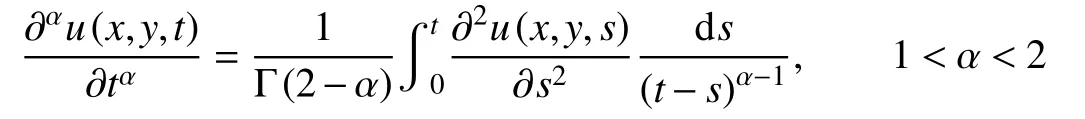
是Caputo 意义下的分数阶导数,Γ (·)为Gamma 函数.
2 无单元Galerkin 法数值离散
2.1 时间离散
令τ 表示时间步长,un=u(x,y,nτ),则Caputo 分数阶导数可利用L1 逼近公式[1, 3]近似为
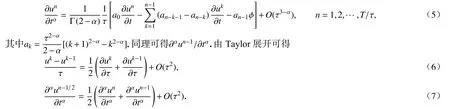
将∂αun/∂tα和∂αun−1/∂tα的表达式代入式(7),并利用式(6)可得

2.2 Galerkin 变分方程
椭圆边值问题(10)可用无单元Galerkin 法迭代求解.由于移动最小二乘近似生成的形函数缺乏插值性质,用无单元Galerkin 法求解问题(10)时,Dirichlet 边界条件的施加较困难[18],可以采用罚函数法来处理.引入罚因子β,则椭圆边值问题(10)可近似为
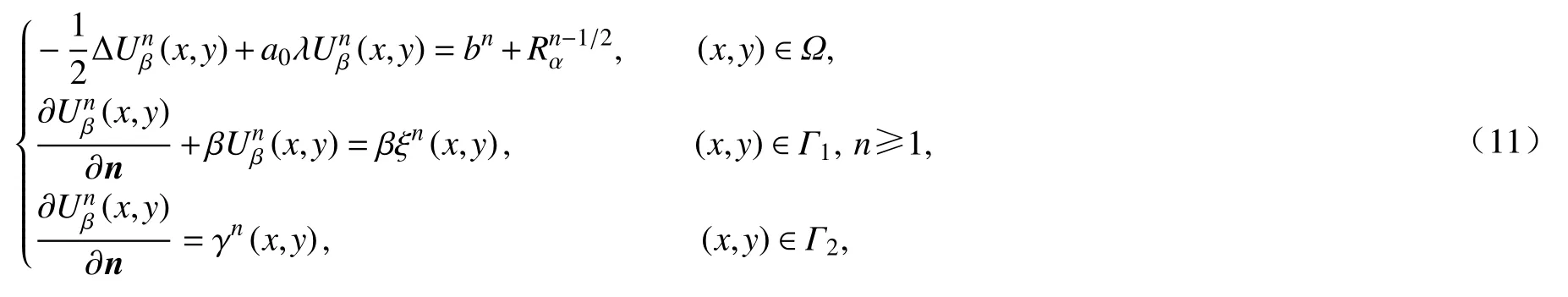
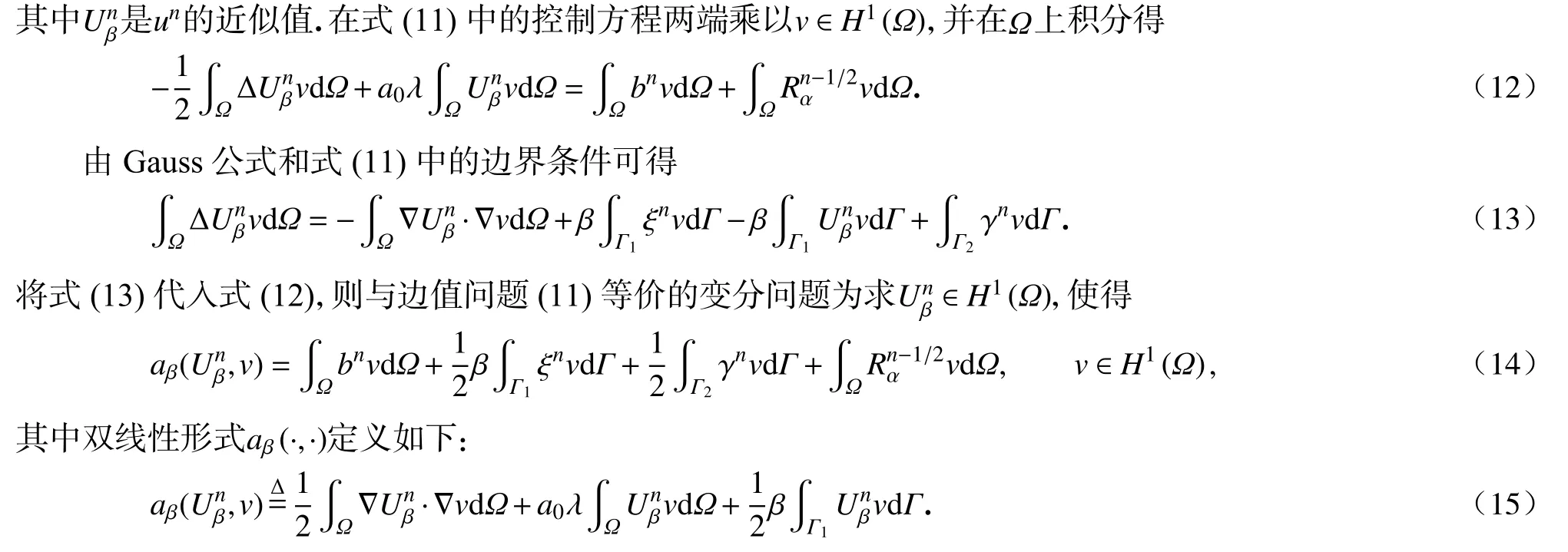
2.3 无网格离散
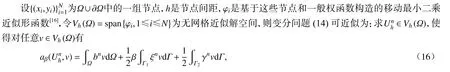
这里
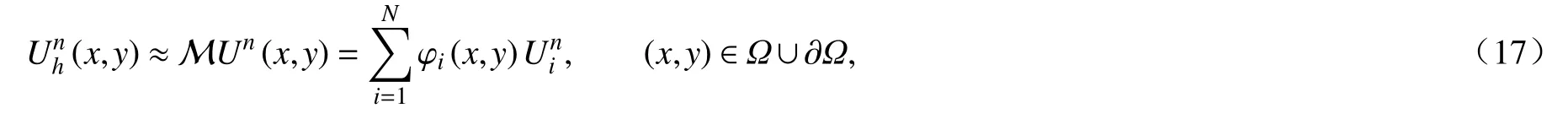
其中 M是移动最小二乘近似中的逼近算子.为了便于数值计算,由Gauss 公式和式(11)中的边界条件,进一步可得
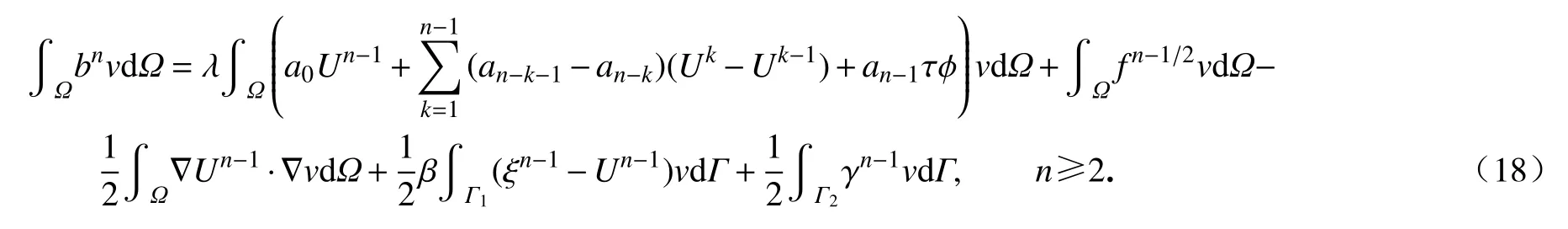
将式(18)代入式(16),可得
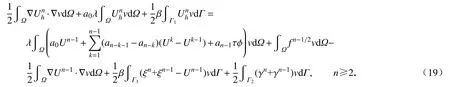
由v的任意性,在式(19)中让v依 次取 φ1, φ2, ···, φN,则椭圆边值问题(10)的无网格离散为
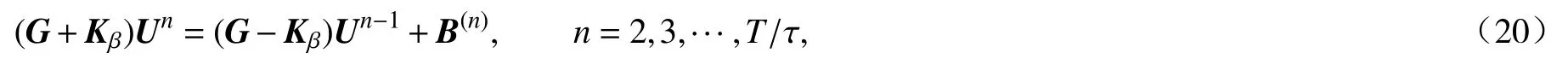
其中
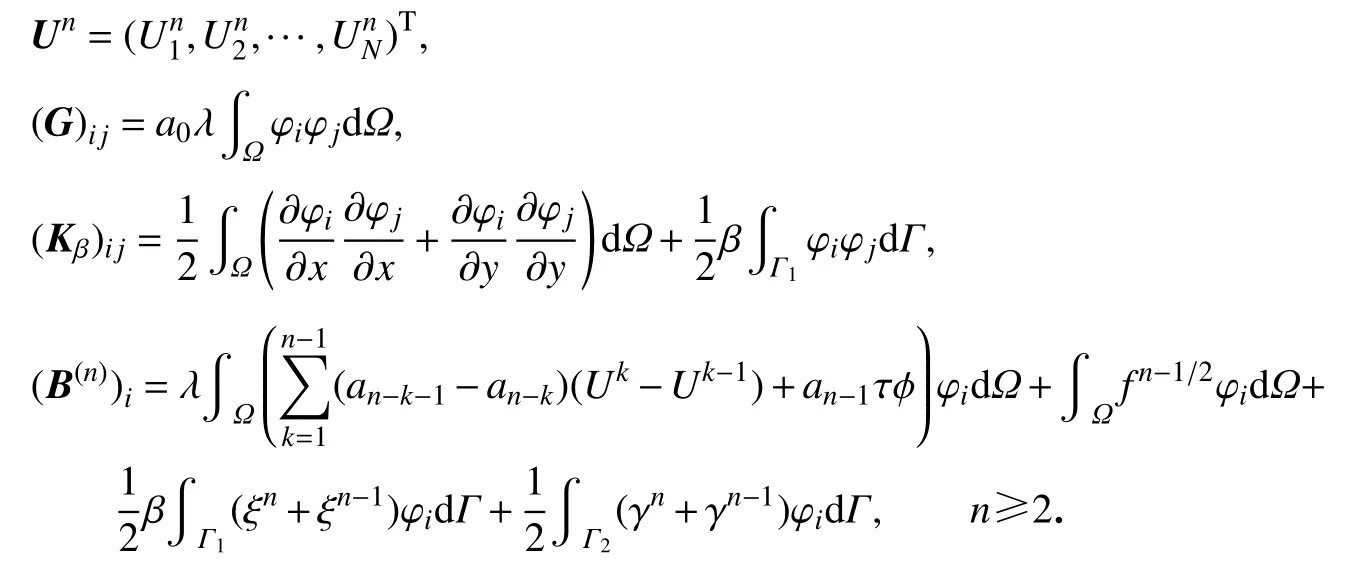
同理可得当n=1时,椭圆边值问题(10)可离散为如下线性代数方程组:

其中
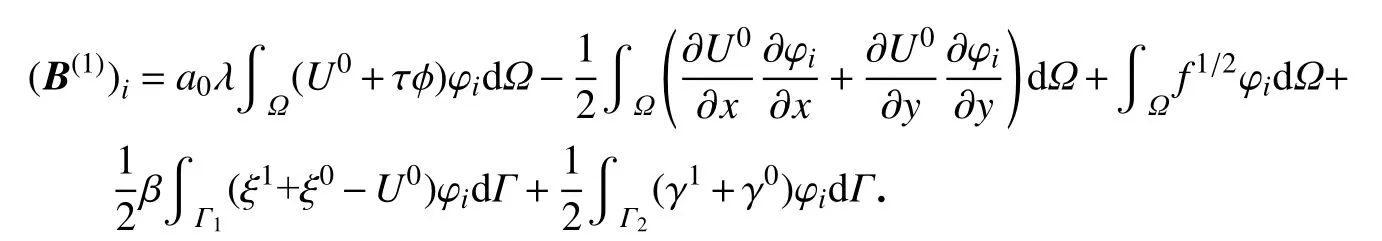
由方程组(21)可以依次迭代求解得到Un.最终,由式(17)可以求出时间分数阶扩散波方程的无单元Galerkin 法近似解.
3 误差分析
定理1设un∈Hq+1(Ω) 是 问题(10)的解析解,为近似变分问题(16)的数值解,则时间分数阶扩散波方程的无单元Galerkin 法有如下误差:
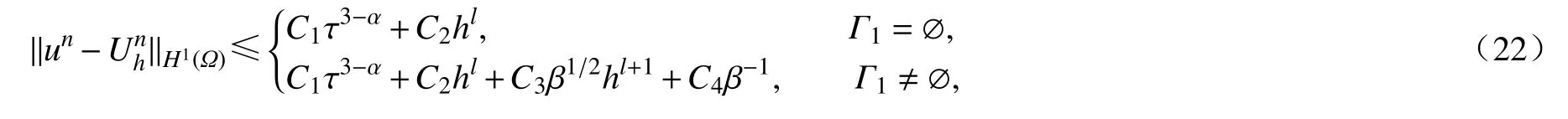
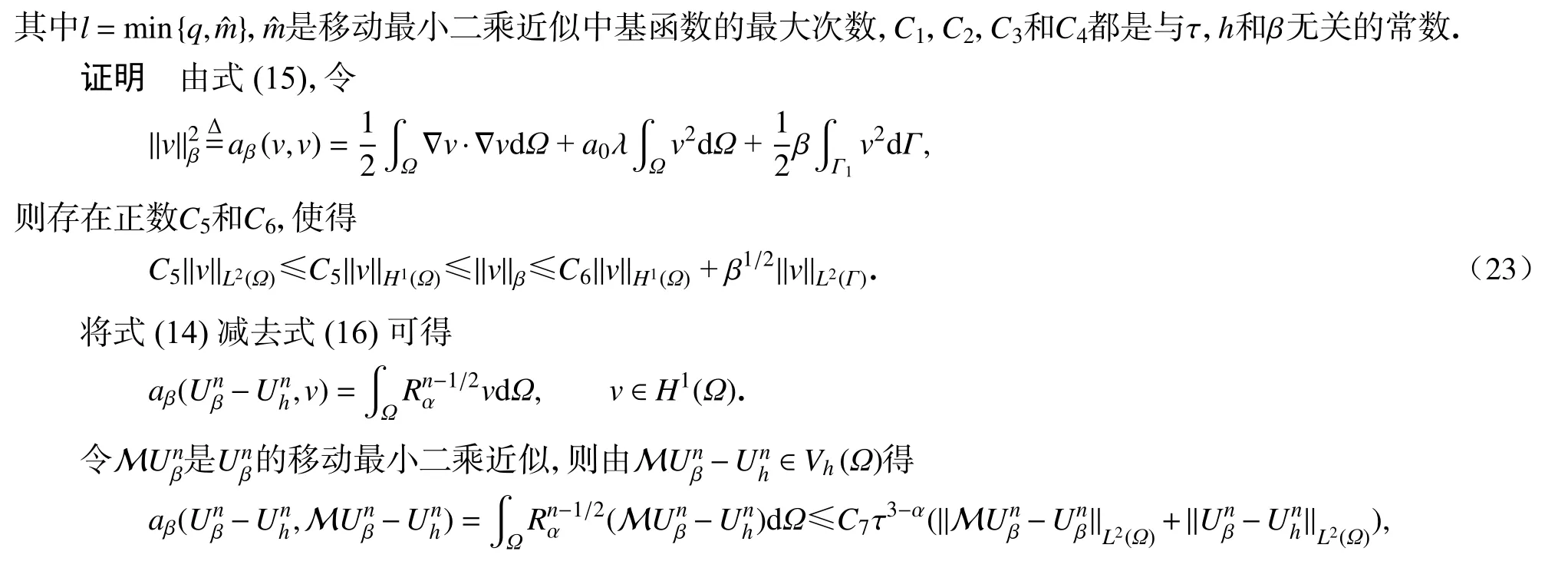
所以
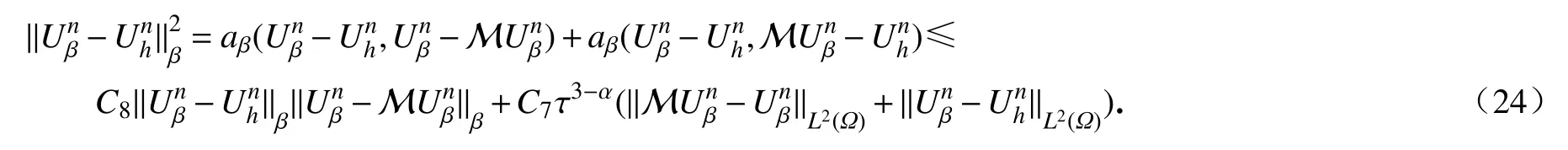
由文献[16]可得


4 数值算例
4.1 算例1
考虑如下时间分数阶扩散波方程[8]:
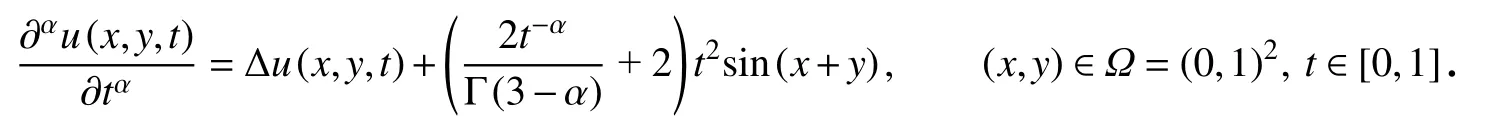
初始条件和边界条件分别为
u(x,y,0)=0, (x,y)∈Ω,
u(x,y,t)=t2sin(x+y), (x,y)∈∂Ω,t∈[0,1].
该问题的解析解为u(x,y,t)=t2sin(x+y).
图1 给出了 α =1.65,h=1/50和 τ =1/40 时,无单元Galerkin 法获得的近似解Uh和 误差 |Uh−u|,数据显示误差小于 1 .5×10−4,说明该方法的计算精度较高.为了研究罚因子 β 对误差的影响,图2 给出了 α=1.65,τ=1/200 时 ,常数罚因子 β 和变化罚因子 β =Cβh−2对误差和收敛性的影响.罚因子β 取为常数时,太大或太小都会让误差增加;罚因子 β =Cβh−2随着空间步长h变 化时,误差始终随着空间步长h的减小而减小,在后面的计算中选取罚因子β =102h−2.
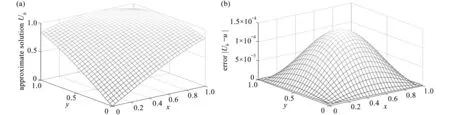
图1 算例1 在α =1.65,h =1/50 和τ =1/40时的近似解和误差:(a) 近似解;(b) 误差Fig.1 Graphs of approximate solutions and resulting errors with α = 1.65, h =1/50 and τ =1/40 in example 1: (a) the approximate solutions;(b) the resulting errors
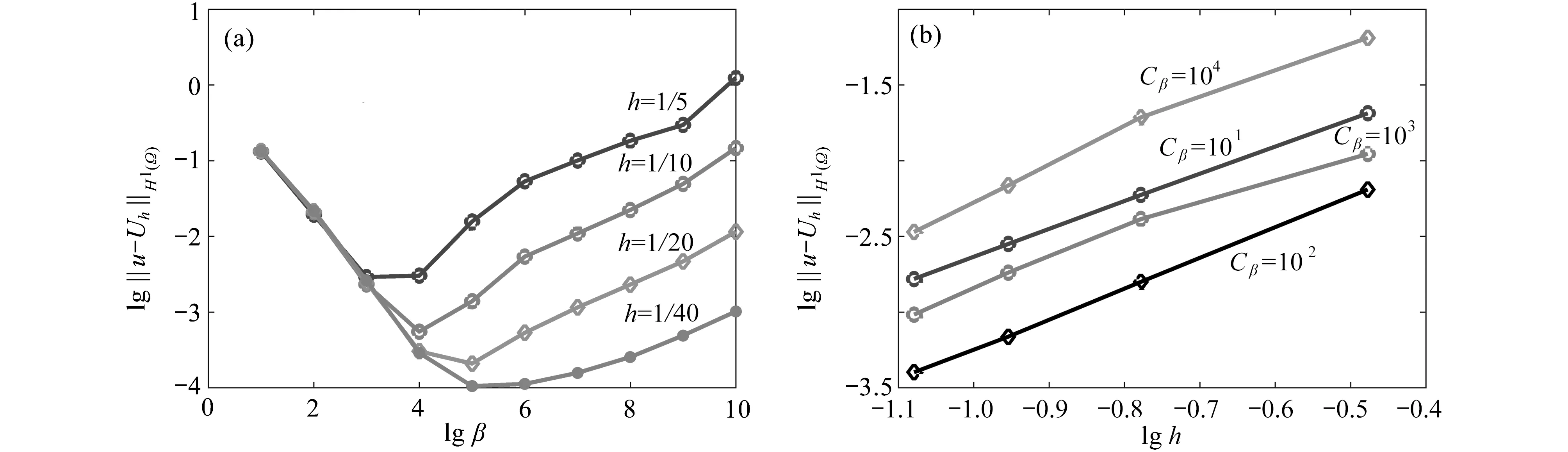
图2 常数罚因子β 和变化罚因子β =Cβh−2 对误差和收敛性的影响:(a) 常数罚因子β ;(b) 变化罚因子β=Cβh−2Fig.2 The error and convergence for fixed penalty factor β and variable penalty factor β =Cβh−2 : (a) for fixed penalty factor β ;(b) for variable penalty factor β=Cβh−2
当 α =1.65, 1.75,1.85,图3(a)给出了h=1/20 时 ,无单元Galerkin 法关于时间步长τ 和 空间步长h的收敛性;图3(b)给出了 τ=1/1 000时 ,无单元Galerkin 法关于空间步长h的 收敛性.图3(a)使用的时间步长 τ为1/8,1/16,1/32,1/64;图3(b)使用的空间步长h为1/2,1/4,1/8,1/16,对应的节点个数为9,25,81,289.图3(a)和(b)中的数值结果分别表明,无单元Galerkin 法关于时间步长和空间步长都得到了很好的收敛结果.
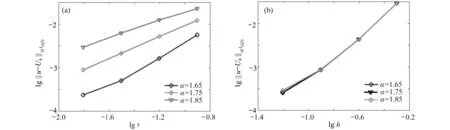
图3 算例1 关于时间步长τ 和空间步长h 的收敛性:(a) 时间步长τ;(b) 空间步长hFig.3 The convergence with respect to time step τ and spatial step h in example 1: (a) for time step τ; (b) for spatial step h
影响域半径可设置为Sscale·h[9,17],其中Sscale是控制影响域大小的参数.当 τ =1/10 和h=1/20时,图4 展示了Sscale对误差的影响,结果表明,影响域大小对误差的影响较小,在后面的计算中选取Sscale=2.5.表1 比较了无单元Galerkin 法(EFG)和有限元法(FEM)[8]在不同分数阶情况下的L∞误差,结果表明无单元Galerkin 法具有更高的计算精度.
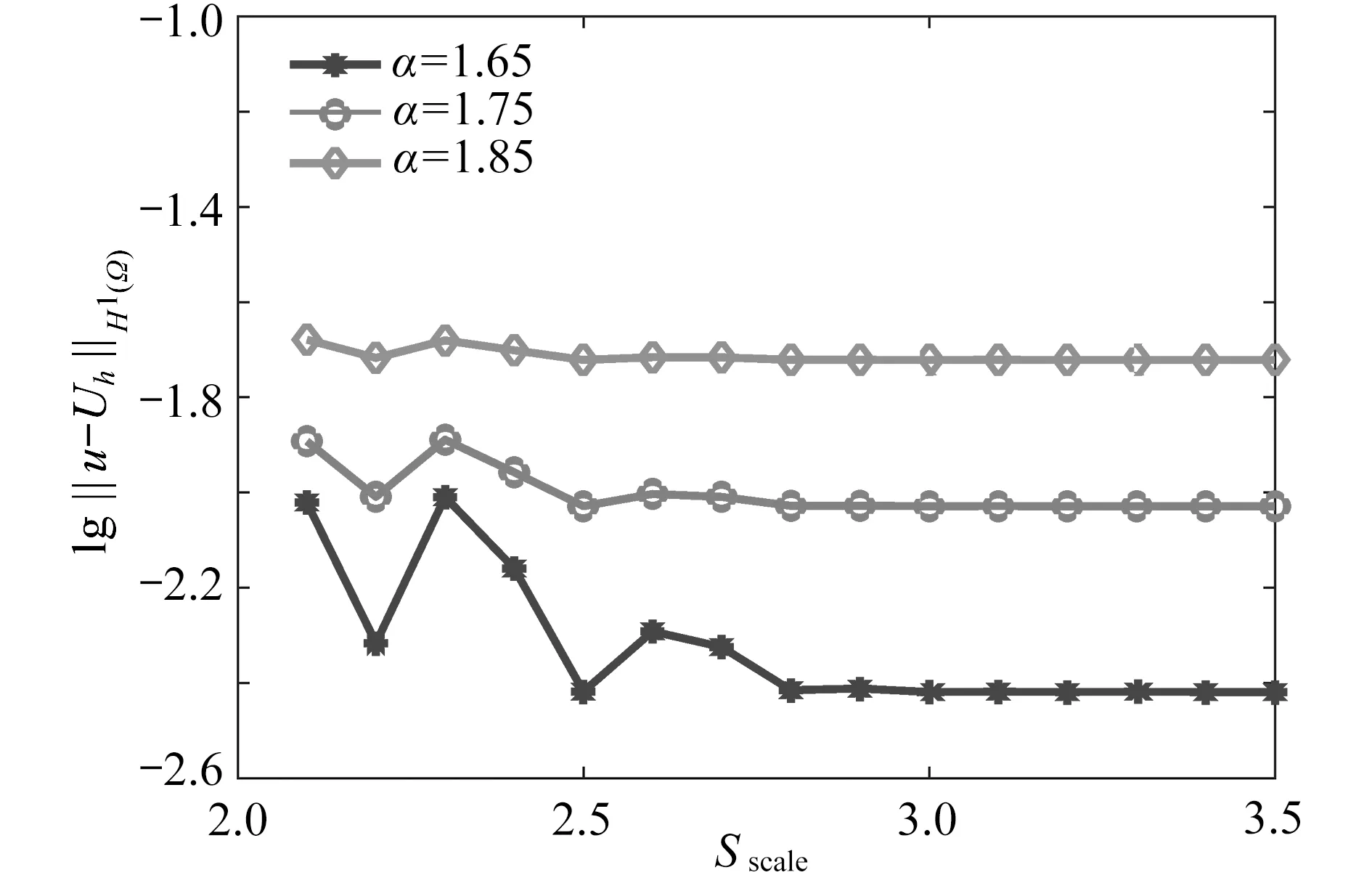
图4 影响域参数Sscale 对误差的影响Fig.4 Effects of influence domain parameter Sscale on errors
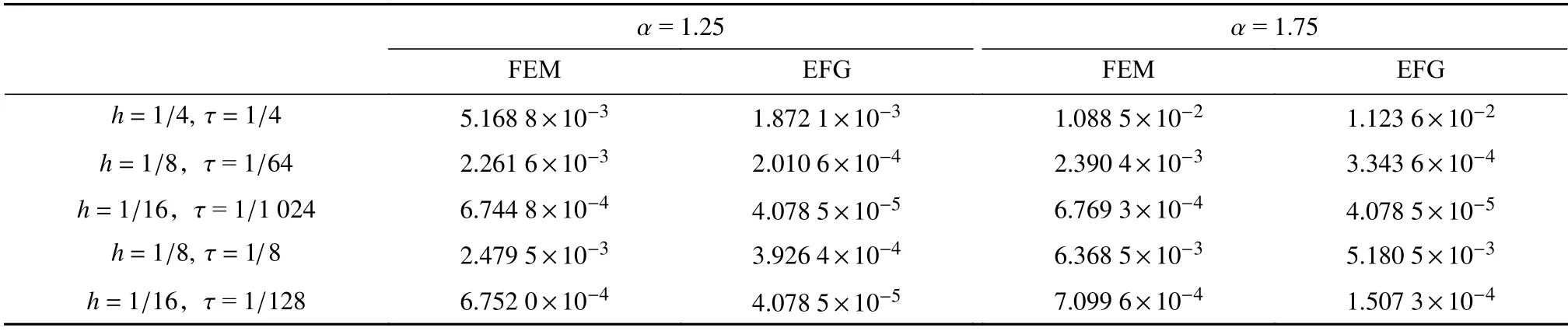
表1 比较有限元法和无单元Galerkin 法的 L∞误差Table 1 Comparison of L∞ errors between the finite element and the element-free Galerkin methods
4.2 算例2
考虑如下时间分数阶扩散波方程[8]:
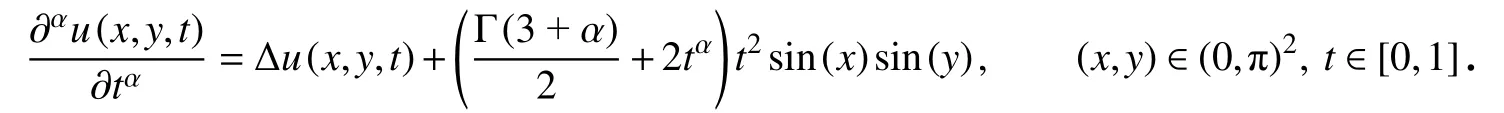
初始条件和边界条件分别为
u(x,y,0)=0, (x,y)∈Ω,
u(x,y,t)=0, (x,y)∈∂Ω,t∈[0,1].
该问题的解析解为u(x,y,t)=t2+αsin(x)sin(y).
当 α =1.5时 ,图5(a)和(b)分别给出了h=π/40和 τ =1/256, 无单元Galerkin 法(EFG)关于时间步长τ 和空间步长h的收敛性.为了比较,图5 同时给出了Galerkin 有限元法(Galerkin FEM)[8]和交替方向隐式有限元法(ADI FEM)[6]的计算结果.数值结果表明无单元Galerkin 法得到了很好的收敛结果,并且比两种有限元法的计算精度更高.表2 中比较了当 α=1.25,h=π/40时,Galerkin 有限元法[8]、交替方向隐式有限元法[6]和无单元Galerkin 法的L2误差,显然无单元Galerkin 法计算精度更高.
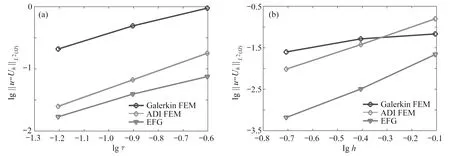
图5 算例2 关于时间步长τ 和空间步长h 的收敛性:(a) 时间步长τ;(b) 空间步长hFig.5 The convergence with respect to time step τ and spatial step h in example 2: (a) for time step τ; (b) for spatial step h

表2 比较h =π/40时 ,三种方法的 L2误差Table 2 Comparison of L2 errors obtained from 3 numerical methods with h=π/40
5 结 论
本文构造了数值求解时间分数阶扩散波动方程的无单元Galerkin 法,详细推导了该方法的计算公式和理论误差.误差理论表明,数值解的误差与时间步长τ、空间步长h和 罚因子β 有关,并且在时间方向和空间方向的收敛速率分别约为O(τ3−α)和O(h2).数值算例验证了该方法的有效性和理论分析结果,并且数值结果表明本文方法比有限元等方法拥有更高的计算精度.本文采用了L1 公式对时间变量进行离散,未来还可以研究利用L(1-2)公式、加权位移的G-L 公式等高阶数值解法去离散时间变量,同时还可以尝试结合更多的无网格方法去构建求解时间分数阶扩散波方程的时空高阶格式.另一方面,本文所研究的时间分数阶仅为常数,未来还可以对变时间分数阶微分方程的数值求解进行研究.

