旋转输液管动力稳定性理论分析*
张 博, 史天姿, 张贻林, 孙东生, 袁从敏, 丁 虎, 陈立群
(1.长安大学 理学院,西安 710064;
2.上海大学 上海市应用数学和力学研究所,上海 200072;3.台山核电合营有限公司,广东 台山 529228)
引 言
重型燃气轮机是迄今为止效率最高、能量密度最大的热-功转换类发电设备[1],被誉为工业皇冠上的明珠,是多学科交叉的典范.而旋转叶片是重型燃气轮机的关键组成部分.随着科学技术的迭代更新,对燃气轮机热效率的要求越来越高,涡轮叶片的工作温度不断升高,涡轮进口温度达到了1 977 K,未来可能更高[2],为了避免叶片不被过早烧毁,工程师在涡轮叶片内部布置了复杂的冷却通道系统[3].为了合理设计含有冷却通道的涡轮叶片,针对这类结构建立精确的动力学模型,准确掌握其振动特性显得尤为必要.
现有文献中通常将涡轮叶片简化为形式各异的旋转梁[4-5]、旋转板[6]或者旋转壳[7-8],用来分析其线性或非线性动力学行为.郑彤和章定国等[9]将叶片简化为柔性薄板,建立了一次近似耦合动力学方程.Zhang 等[10]考虑叶片预变形效应,研究了旋转预扭梁在2∶1[11]或3∶1[12]内共振情况下的非线性动力学响应.Oh 和Yoo[13]建立了旋转叶片热弹耦合动力学模型,揭示了叶片服役热环境以及内部冷却液温度对叶片振动特性的影响,但并未涉及到内部流体对叶片振动的影响.
以上有关旋转叶片的研究,都没有考虑内部流体对叶片动力学特性的影响.但是,涡轮叶片的振动问题严重影响着工程系统的安全运行,亟需揭示其内部冷却液对其振动特性的影响.而早在20 世纪60 年代,Benjamin[14]基于开放系统的Hamilton 原理建立了输液管道的动力学模型,报道了管内流体对管道振动稳定性影响.Gregory 与Paidoussis[15]在Benjamin 的基础上研究发现,当流速超过某临界值时,管道将从流体源源不断获得能量并发生颤振失稳.王乙坤等[16]研究了脉动内流作用下管道的参数共振行为,揭示了输液管丰富的动力学现象.近期,易浩然等[17]考虑集中质量的影响,建立了悬臂输液管动力学模型,从理论和实验两方面探讨了输液管振动特性的演变规律.文献[18-19]报道了管道内部流动的流体将诱发结构发生内共振,不同模态之间存在能量交换关系.此外,国内学者如黄玉盈等[20]、金基铎等[21]、徐鉴等[22-23]和王琳等[24]在输液管动力学行为领域也做了大量有益的工作.
在旋转输液管领域,国际上已有一些相关的研究报道.根据管道旋转轴线方向与管道轴线的相对位置关系,大致分为两类:一类是管道旋转轴线方向与管道轴线重合;另一类是二者方向相垂直.前者相当于自旋的输液管,相关研究比较充分,经常用于油气开采中的深井钻头[25-28].第二类类似于旋转叶片模型,相关研究较少.Panussis 和Dimarogonas[29]采用Galerkin 和Hamilton 原理,率先研究了水平旋转输液管面内与面外耦合振动.Yoon 和Son[30]研究了变转速过程中,具有端部质量的旋转输液管在轴向和横向上的动力学响应.Wang 和Zhong[31]建立了旋转输液管的动力学模型,研究了蜻蜓翅膀血液循环对其飞行能力影响,发现在特定血流条件下,蜻蜓翅膀会失去稳定性.
通过文献调研不难发现,结构内部流体流动会显著影响结构的动力学行为,但考虑内部流体流动的旋转叶片模型相关研究还较少.为了准确掌握具有内部冷却通道的涡轮叶片的动力学特性,揭示内部流体对旋转叶片动力学特性的影响,本文利用Lagrange 原理,研究了基于Euler-Bernoulli 梁理论的悬臂式旋转输液管的自由振动特性,讨论了流体流速、端部质量、转速等系统参数对旋转输液管自由振动特性的影响规律.
1 模型描述与假设
本文建立的动力学模型如图1 所示,长为L且具有端部质量Tm的旋转空心叶片,绕轮毂中心以恒定角速度Ω转动,轮毂半径为r,这里假定叶片为内外径分别为Rin和Rout的空心圆截面管道,管道单位长度质量为m,管道内部流体相对于管道的流速为U,其单位长度质量为M.建立两套坐标系来描述结构的运动与变形:① 固结于轮毂中心的全局直角坐标系OXYZ;② 固结于旋转管道根部截面中心,x轴与管道中轴线重合并连同管道一起旋转的随转坐标系oxyz,管道在x,y方向上的变形分别用w1和w2表示.为了简化分析,引入如下假设:1)忽略管道剪切变形和转动惯量的影响,采用Bernoulli-Euler 梁理论描述其位移场;2)忽略管道在z方向的变形,即振动发生在一个平面xoy内;3)管道内流体为定常不可压缩的无黏流体;4)管道是均匀、各向同性的线弹性材料.
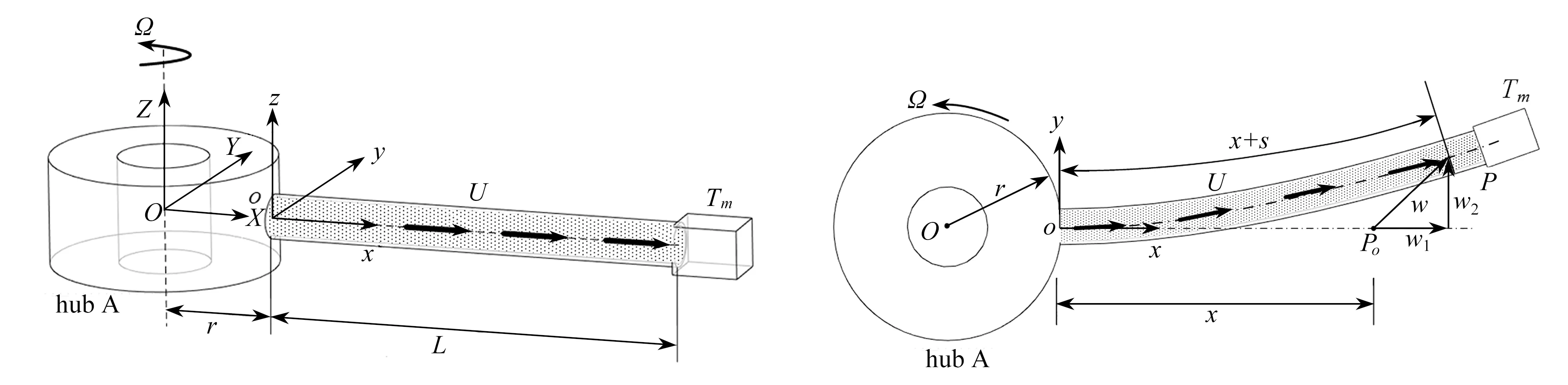
图1 旋转输液管动力学模型Fig.1 The sketch for a rotating pipe conveying fluid
2 运动学方程
假设全局坐标系下,X,Y,Z方向上的单位向量分别为i,j,k, 则管道上任意点P的速度矢量为

其中q1i,q2i为管道广义位移,N1,N2为选取的模态函数个数,φ1i, φ2i分别为轴向和横向两个方向上选取的试函数.需要说明的是,端部质量的存在会影响悬臂管的力边界条件,本文采用假设模态法,只需满足位移边界条件即可,故选取悬臂梁轴向和横向振动的模态函数作为试函数,其具体表达形式如下:
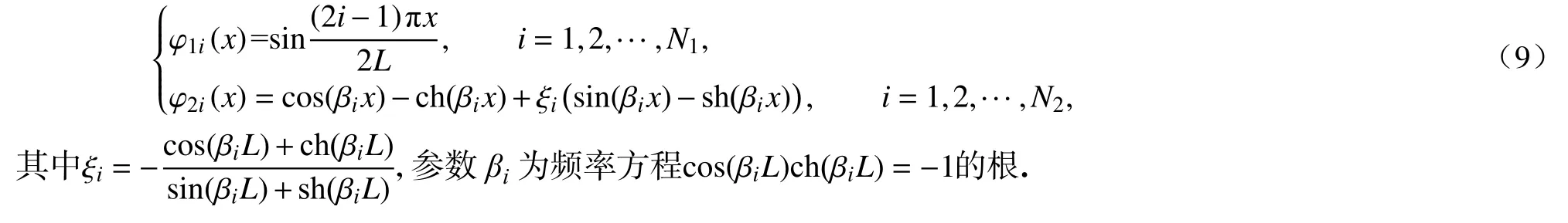
系统的Lagrange 函数为

将式(3)~(7)代入式(10),采用式(8)将连续体离散,结合Lagrange 原理即可得到矩阵形式的动力学方程:
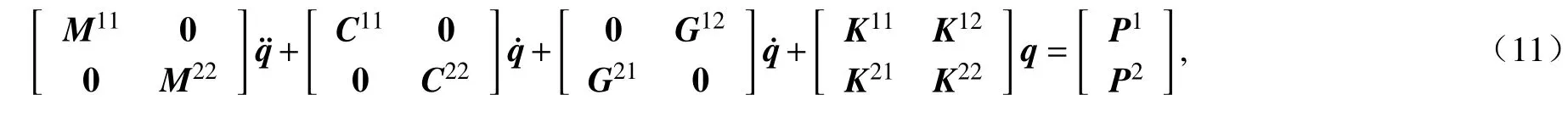
写成紧凑形式为

3 结果与讨论
本文的数值算例为一个空心圆截面(内外半径分别为Rout,Rin)的旋转叶片,叶片和内部流体的体积密度分别为ρp和ρf,则单位长度管道和流体的质量分别为后面的数值算例中,若无特殊说明,取具体的参数设置见表1.

表1 系统参数设置Table 1 System parameter values
为了使结果具有普遍性,按照文献引入无量纲参数:
首先,研究本文模型假设模态法的收敛性.图2 对比了选取不同试探函数数目下系统的Argand 图,其中各阶模态所对应的曲线上标记了无量纲流速数值.发现对于N1=N2=5,当流速较小时,流体给系统各阶模态引起了阻尼效应,当流速增加到2.40 时,第一阶模态轨迹穿越横轴,预示着管道将发生颤振失稳.当流速增加到9.90 时,第三阶模态轨迹穿越横轴.在该算例中,第二阶模态始终未发生失稳,与文献[24]中报道的两端固支输液管第二阶模态先失稳不同.对比发现,不同试探函数个数下,得到的系统Argand 图大致类似,只有临界流速存在数值差别.当试探函数个数取10 时,临界流速收敛.因此后面的数值算例中取N1=N2=10.
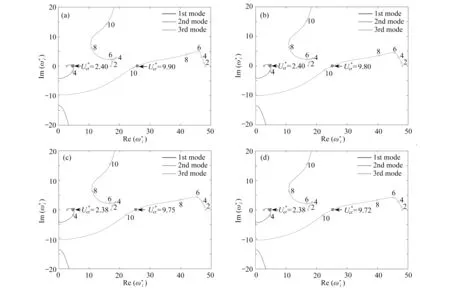
图2 不同试探函数个数下前三阶特征根轨迹曲线 (Tm* = 0,Ω* = 0):(a) N1 = N2 = 5;(b) N1 = N2 = 8;(c) N1 = N2 = 10;(d) N1 = N2 = 12Fig.2 The trajectories of the 1st 3 eigenvalues for different trail function numbers (Tm* = 0, Ω* = 0): (a) N1 = N2 = 5; (b) N1 = N2 = 8;(c) N1 = N2 = 10; (d) N1 = N2 = 12
为了验证模型的正确性,特将本文计算结果与文献[33]报道的结果做一对比,具体如表2 所示.由表格数据可见本文模型具有较高的计算精度.

表2 系统第一阶无量纲固有频率本文计算值与文献对比(ρf = 0)Table 2 Comparison of the 1st natural frequencies obtained from the present study and the reference (ρf = 0)
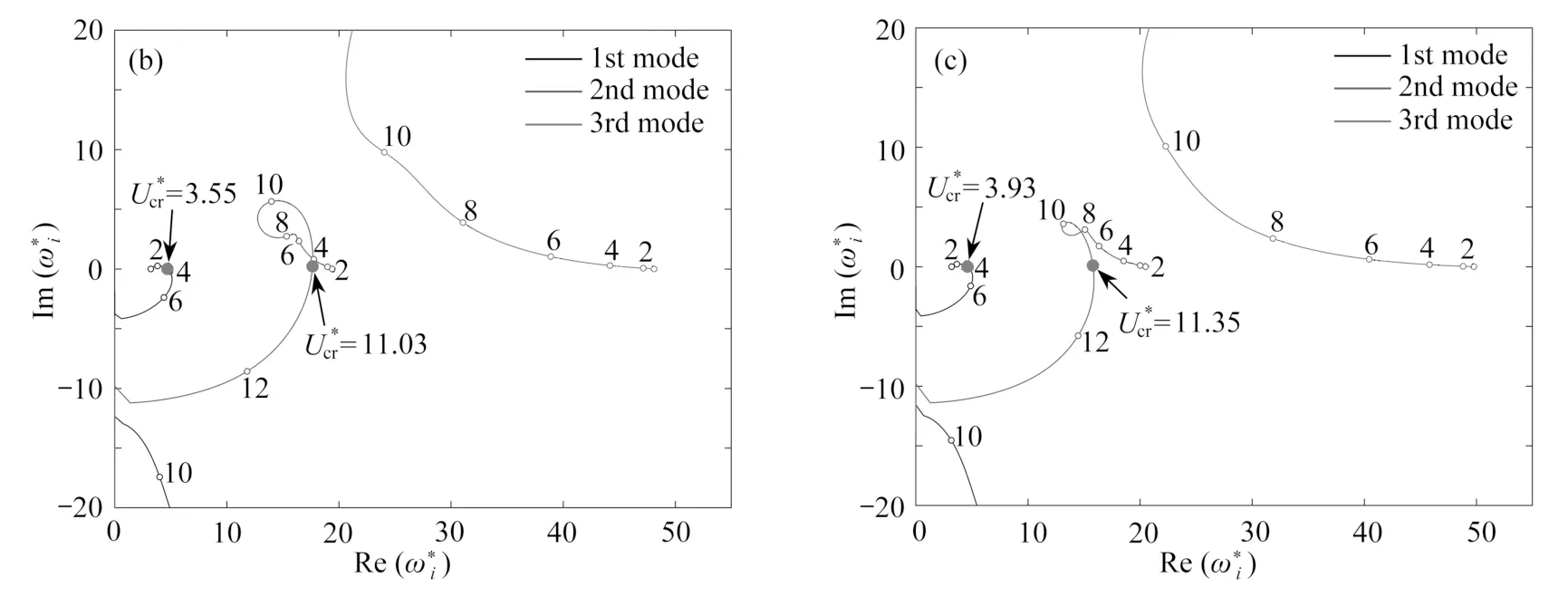
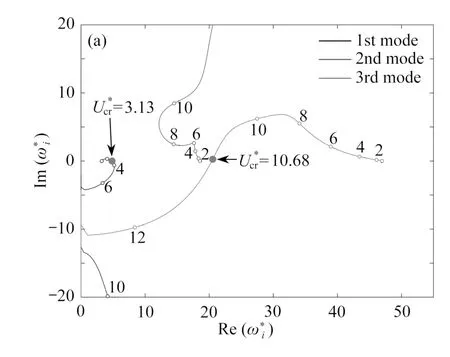
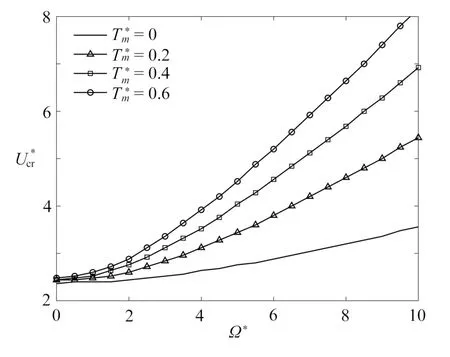
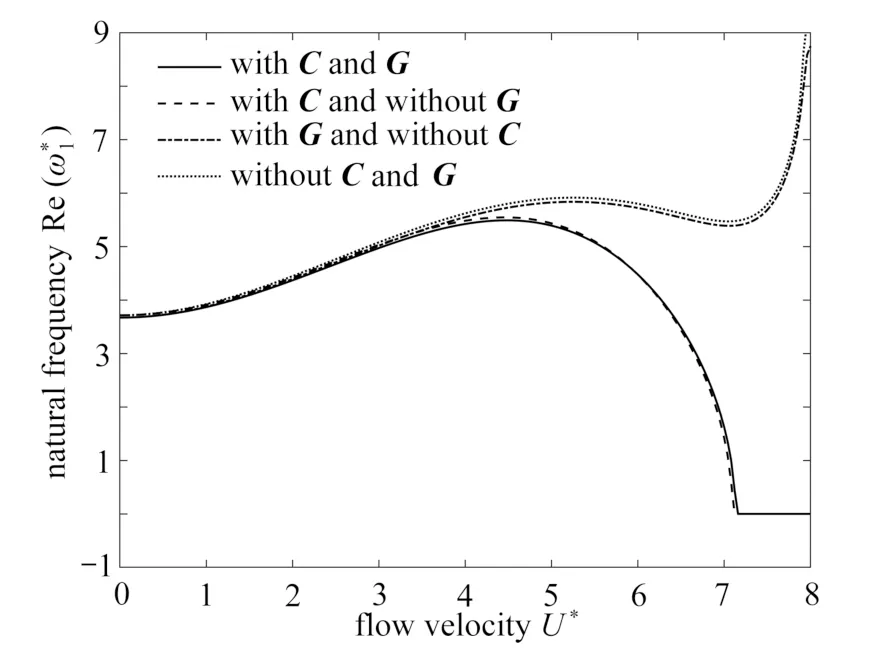
图3 给出了三组不同转速下系统前三阶特征根轨迹曲线.发现随着转速增大,旋转输液管系统特征根轨迹向横轴正方向移动.实际上,旋转离心效应对结构存在刚化效应.当转速足够大(Ω*=8),流速存在一个区间(7.90 图3 转速对特征根轨迹的影响 (Tm* = 0):(a) Ω* = 4;(b) Ω* = 8;(c) Ω* = 12Fig.3 Effects of the rotating speed on the eigenvalue trajectories (Tm* = 0): (a) Ω* = 4; (b) Ω* = 8; (c) Ω* = 12 图4 和图5 分析了端部集中质量对系统动力学特性的影响.当端部集中质量足够大,系统第三阶模态在很高流速下也是稳定的,但第二阶模态开始出现颤振失稳(图4(b)、4(c)).临界流速随集中质量增大而增大.由图5 可见,旋转输液管的第一阶临界流速随转速增大而提高,且其变化率随端部质量增大而增大.实际上,由于旋转运动在输液管内部产生拉应力对结构存在“应力刚化”效应,使得结构的刚度变大,稳定性提高,内部流体流动使得结构颤振失稳更困难.而端部质量的出现进一步强化了“应力刚化”效应,因此曲线斜率随端部质量增大而增大. 图4 端部集中质量对特征根轨迹的影响 (Ω* = 4):(a) Tm* = 0.2;(b) Tm* = 0.4;(c) Tm* = 0.6Fig.4 Effects of the tip mass on the eigenvalue trajectories (Ω* = 4): (a) Tm* = 0.2; (b) Tm* = 0.4; (c) Tm* = 0.6 图5 不同端部集中质量下临界流速随转速的变化规律 (Ω* = 4)Fig.5 Variations of the critical fluid velocity with the rotating speed for different tip masses (Ω* = 4) 为了揭示运动方程(11)中矩阵C和G对系统动力特性的影响规律,在图6 中绘制了四种情形下(包括同时考虑C,G矩阵,仅考虑C矩阵,仅考虑G矩阵和忽略C,G矩阵),系统第1 阶固有频率随流速的变化情况.通过对比不难发现,陀螺矩阵G对系统固有频率影响很小.事实上,对于该算例旋转输液管,其轴向尺寸是横向尺寸的40 倍,属于细长梁,因此旋转运动引起的轴向及横向运动间的耦合效应很微弱.此外对于该算例,当无量纲流速U*< 4 时,对称矩阵C对系统动力学特性影响不大.当无量纲流速U*超过4 时,考虑矩阵C影响的曲线跟忽略矩阵C影响的曲线发生明显分离.前者持续下降,且当流速约为7.12 时降为0,特征值变为纯虚数.而忽略矩阵C影响,当流速U*> 7 时,系统第1 阶固有频率迅速升高.由此证明了流体运动对旋转管道的动力学特性有显著影响. 图6 矩阵C 和G 对系统第一阶固有频率的影响 (Ω* = 4,Tm* = 0.2)Fig.6 The effects of matrices C and G on the system 1st natural frequency(Ω* = 4, Tm* = 0.2) 图7 绘制了系统前三阶无量纲固有频率随流速的变化曲线,同时为了探析旋转输液管模型发生内共振的可能性,图中画出了2ω1*,3ω1*,2ω2*随流速的变化曲线.图中出现了一些曲线间的交点,例如,当流速U*=3.72 时,3ω1*和ω2*相交,即3ω1*= ω2*,预示系统存在3∶1 内共振;当流速U*= 11.17 时,2ω1*和ω2*相交,即2ω1*= ω2*,预示系统存在2∶1 内共振.在该算例流速范围内(0~20)ω1*和ω2*未相交.此外系统第三阶固有频率轨迹同前两阶模态也存在多个交点.特别地,当流速U*= 10.22 时,曲线3ω1*,ω2*和ω3*交汇于同一点.预示该条件下系统前三阶模态存在复杂的能量交换机制. 图7 旋转输液管前三阶固有频率随流体流速的变化规律 (Ω* = 2,Tm* = 0.2)Fig.7 The variations of the 1st 3 natural frequencies of the rotating pipe (Ω* = 2, Tm* = 0.2) 本文采用Lagrange 原理建立了内部包含流体通道的旋转梁的动力学模型,应用假设模态法得到了经过离散的矩阵形式表达的系统运动方程,并确定了研究方法具有收敛性.研究发现,当流体速度超过一定数值时,旋转输液管将发生颤振失稳.本文还揭示了转速、端部质量对旋转管道系统临界流速的影响.此外,还发现在一些特定的参数组合下,可能会诱发系统低阶模态之间不同形式的内共振.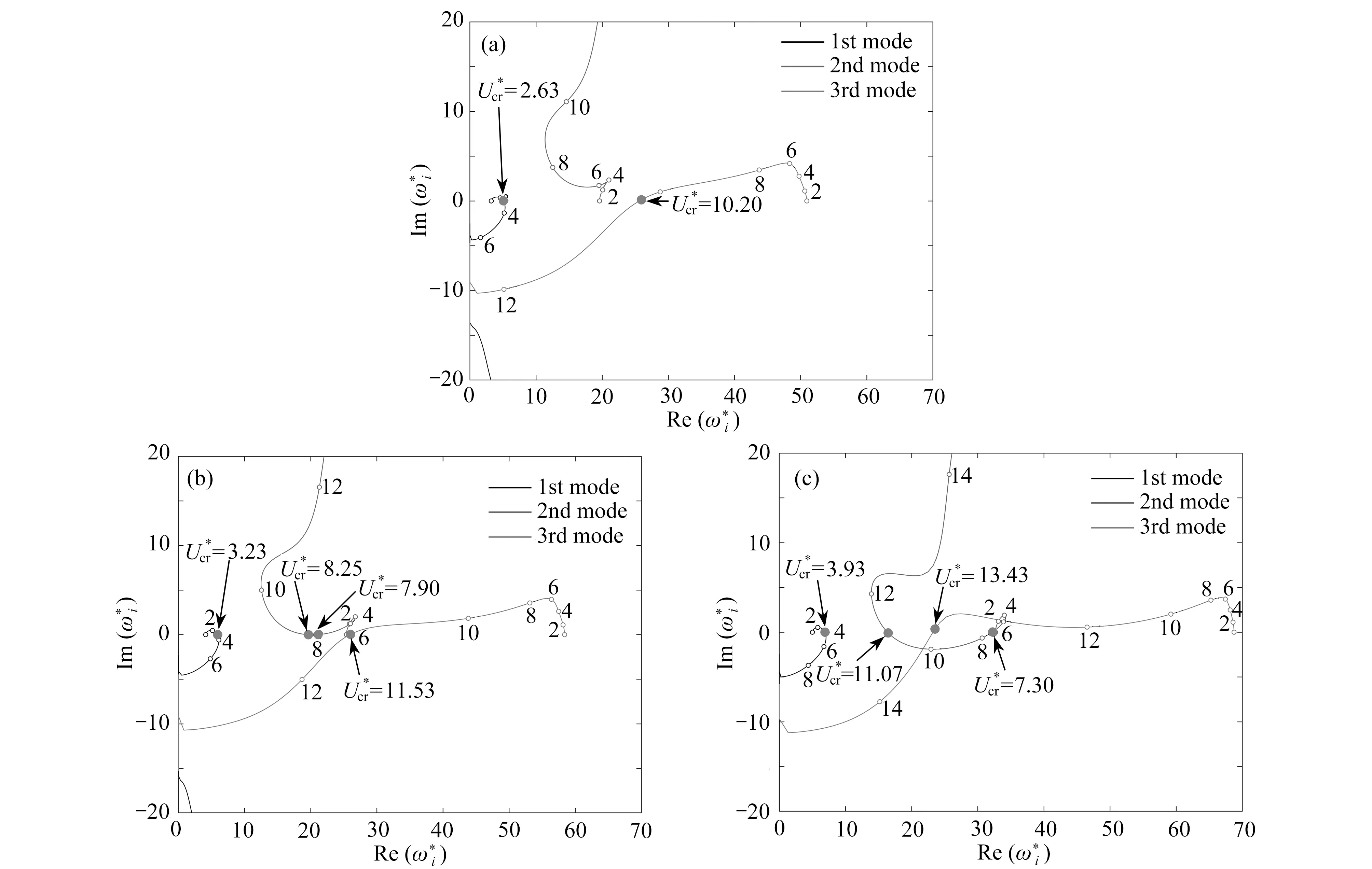

4 结 论

