基于CSI的三维联合参数估计算法

杨小龙 佘 媛 周 牧 田增山 王嘉诚

(重庆邮电大学通信与信息工程学院 重庆 400065)

1 引言

近年来，随着无线局域网(Wireless Local Area Network, WLAN)的广泛部署和移动智能终端的逐渐普及，无线局域网逐渐成为人们日常生活中必不可少的部分，而基于Wi-Fi的无线局域网技术在家庭、商城、机场等人们聚集的场所已经得到了广泛应用。Wi-Fi不仅能够用于数据通信，同时还可以用来进行环境感知，推断周围环境的变化等[1]。由于室内环境的复杂性，信号在实际的传播过程中，无法直接沿着视距到达接收端，而是沿着室内环境中家具、办公用品、墙壁以及运动人体等障碍物形成的多条反射路径传播。这种传播模式使得接收到的Wi-Fi信号中包含了周围的环境信息，即Wi-Fi信号中包含了信道状态信息(Channel State Information, CSI)。因此，本文通过对CSI进行分析，对信号的相关参数进行估计，可以实现对周围环境检测。由于Wi-Fi的环境感知能力，目前学术界已经涌现了许多新兴的应用，如使用Wi-Fi进行人体检测、室内定位、行为识别、摔倒检测等。

现有的信号参数估计的方法有基于最大似然估计的参数估计算法、基于子空间分解的多重信号分类(MUltiple SIgnal Classification, MUSIC)算法[2,3]等。MUSIC算法因为拥有多信号同时测向能力以及对天线波束内的信号的高分辨测向能力而广泛应用于参数估计中。现有的利用MUSIC算法进行参数估计的方法大都是1维的信号到达角(Angle of Arrival, AoA)估计和联合AoA、飞行时间(Time of Flight, ToF)或者联合AoA、多普勒频偏(Doppler Frequency Shift, DFS)的2维参数估计。在Schmidt等人提出MUSIC算法之后，文献[4]将MUSIC算法和CAPON进行结合，首先使用CAPON估计由多个AoA组成的AoA组，然后使用基于波束空间的MUSIC算法估计AoA组中的单个AoA。Wang等人[5]提出了一种CSI分量重构算法来进行穿墙场景下的AoA估计，该方法通过信道参数估计、重构和抵消，可以分离出每个传播路径的CSI，并估计目标反射的AoA。Zheng等人[6]对AoA进行估计并用与AoA估计精度相关的相应因子进行加权，提高定位精度。文献[7,8]首先对AoA等参数进行估计，再将AoA作为目标特征利用神经网络进行训练，对目标进行定位。但是仅估计AoA的方法不能分辨信号到达角相同的多个信号源。为了提高信号分辨能力，文献[9-13]提出了联合DFS和AoA以及联合AoA与到达时间(Time of Arrival, ToA)或ToF的2维参数估计方法。这种将到达角和飞行时间或者多普勒进行联合估计的2维参数估计方法在不影响参数估计精度的情况下，提高了阵列的有效孔径和信号分辨能力。

对于现有的1维和2维参数估计方法，由于实际应用中，阵列天线数量有限，限制了AoA估计的分辨能力，且Wi-Fi的有限带宽限制了飞行时间的估计精度。当信号参数相隔较近时，不能分辨多个信号。基于此，文献[14]设计了子空间交替期望最大化算法(Space-Alternating Generalized Expectation maximization, SAGE)，该算法用最大似然估计对AoA, ToF, DFS等参数进行估计，提高了信号的分辨能力。但是SAGE算法依赖于初始值的设置，且分别对每一个参数进行估计容易使参数估计结果陷入局部最优值，影响参数估计精度。因此，针对上述现有系统存在的问题，本文深入研究CSI信号的特性，对CSI中包含的特征参数进行分析，提出了一种联合到达角、多普勒频偏和飞行时间的3维联合参数估计的方法。该方法首先利用不同的天线、载波以及数据包之间的相位关系构造3维矩阵，为了计算简便，对接收到的CSI信息矩阵进行降维处理，将构造的3维矩阵转换为2维矩阵。然后利用提出的3维空间平滑算法对2维矩阵进行平滑，以去除相干信号对参数估计的影响。最后，利用3维联合参数估计算法对3维参数进行估计。该方法对AoA, ToF, DFS 3维参数进行分析，充分利用信号参数，在2维参数估计算法的基础上，增加了参数估计维度，提高了信号的分辨能力。其次，同时对AoA, ToF, DFS进行估计可以避免SAGE算法依次对各个信号的多个参数进行估计时由于误差的传递性对参数估计精度造成的影响，提高参数估计的精度。该方法能够有效地解决1维和2维参数估计中存在的对信号的分辨能力不高的问题，以及基于最大似然估计的参数估计算法会使参数估计结果陷入局部最优值的问题，提高参数估计精度和信号分辨能力，为Wi-Fi的广泛应用提供理论基础。

2 系统模型

假设Wi-Fi接收天线阵列为均匀分布的线阵，阵列天线数量为M，天线之间的间距为d，子载波个数为N，天线阵列接收的数据包的个数为P。存在K(PMN>K)个具有相同中心频率f0的入射源信号分别以入射角θ1,θ2,...,θK入射到该天线阵列，其中θk,0≤θk ≤90◦是第k个入射信号的入射角。信号源sk(t)入射到空间阵列模型如图1所示。

信号源sk(t)经过第n(1≤n ≤N)个子载波入射到接收阵列的第m(1≤m ≤M)根天线上，阵列天线接收到的信号为

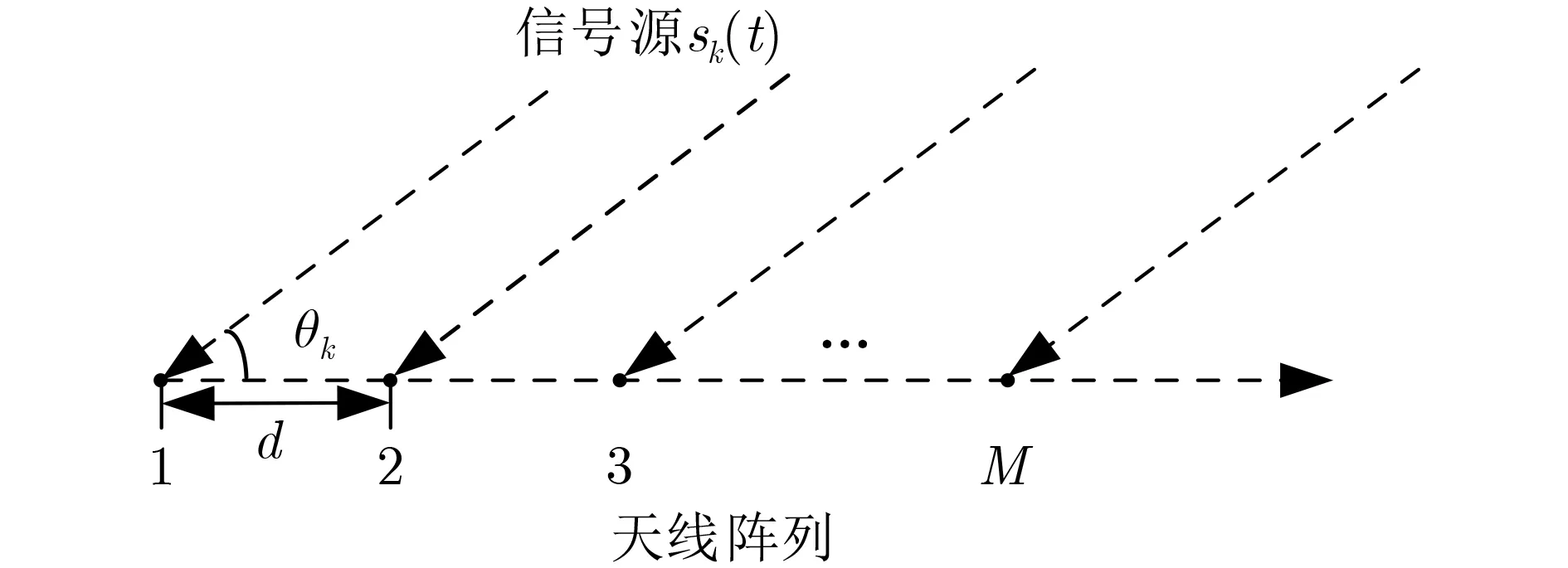
图1 波达方向示意图

3 3维参数估计算法

为了同时解决1维参数估计中天线数量受限导致的AoA估计精度不高以及同时估计的信源个数有限的问题，以及2维参数估计中信道带宽不高导致的ToF估计精度受限的问题，结合多普勒频偏不受天线数量和信道带宽的限制的特性，本文将AoA,ToF和DFS进行结合，提出一种3维估计方法，以提高参数估计精度以及信号分辨能力。

3.1 参数分析

3.2 数据降维与平滑

图2 算法流程图

由于室内环境的复杂性，接收到的信号之间大都存在较大的相关性，同时也存在一些相关性较弱的信号。相干信号的协方差矩阵不是满秩矩阵而不能直接使用MUSIC算法进行参数估计，因此，只要接收信号之间具有相关性，均需要对其进行去相干处理。而对于非相干信号，接收信号之间不存在相关性，不需要利用本文提出的平滑算法进行去平滑处理，直接利用3维参数估计算法即可对AoA,ToF, DFS等参数进行估计。文献[15,16]提出的空间平滑 (Spatial Smoothing Techniques, SST)算法及其改进算法可以去除相干信号之间的相干性。因此，本文利用空间平滑算法对降维后的2维矩阵Y进行处理，得到平滑后的矩阵Y，其维度为L1L2L3×(P −L3+1)(M −L2+1)(N −L1+1)，其中L1,L2,L3分别表示子载波、天线、数据包之间进行平滑的平滑窗大小，具体的算法过程如下：

3.3 空间谱估计

4 3维联合参数估计实验验证

4.1 3维谱峰搜索范围讨论

确定了3个参数的搜索范围之后，就可以在该范围内进行仿真与实测验证算法的性能。

4.2 3维空间平滑算法性能分析

首先，对于3维平滑算法，因为实际环境中不存在完全不相干的信号，所以本文用仿真实验验证3维平滑算法的性能。假设Wi-Fi系统中接收天线阵列存在3根天线，均匀天线之间的间距为λ/2，每根天线上有连续的30个子载波，相邻子载波之间的间隔为1.25 MHz，信号频点为5.7 GHz，从接收到的数据包中选取4个数据包，数据包的发送速率为每秒500个包，信噪比为SNR=10 dB。入射信号源个数为3个，信源参数设为(1 m/s, 45° ,20 ns)，(2 m/s, 30°, 10 ns)，(0 m/s, 60°, 10 ns)。本文进行900次仿真，分别画出AoA, ToF, DFS误差累积分布图，对比去相关前后的参数估计精度。

从图4的仿真结果可以看出，对于相干信号，无论是对AoA, ToF还是DFS的估计，平滑后的估计精度均高于平滑前的估计精度。因为相干信号的存在，影响了噪声子空间的求解，从而极大地影响了参数估计的精度。进行3维平滑之后的信号去除了信号之间的相干性，提高了参数估计精度。

在不同的信噪比下进行仿真对比，如图5所示。

从图5的仿真结果可以看出，随着信噪比的降低，AoA, ToF, DFS的参数估计精度均有一定程度的降低，但是在不同信噪比下，平滑后的参数估计精度均高于平滑前的参数估计精度。

4.3 3维联合参数估计性能实测分析与比较

实验环境为会议室，实验采用搭载Ubuntu操作系统的主机以及安装了Intel 5300网卡的发射机和接收机进行数据的收集，实验收发机及网卡如图6所示。

图3 天线间距大于λ/2的2维参数估计

实验采用1发多收，Intel 5300 网卡有3个数据接收通道，因此接收机上配有3根物理天线，发送端用1根天线进行信号发射，发送端和接收端均采用全向天线，以获得大范围的室内环境信息。为了在有限天线个数的情况下获取最大角度分辨率，实验参数设置为：天线间距为半波长，信号中心频率为5.7 GHz，信号带宽为20 MHz，发包速率为500包/s，子载波数量为30，发射功率为15 dBm。

实验场景如图7所示。

首先对于发送机位置固定的情况对目标参数进行估计。发射机和接收机之间距离5 m，发射机以每秒500个数据包的速率发送数据。采集的数据以包的形式呈现，每个数据包中包含了3根天线30个子载波的CSI数据。对于目标运动的实验场景，分别采集了发射机位于接收机的左侧和右侧两种情况，图7中给出了发射机位于接收机的左边的场景图，实验开始时，目标静止2～3 s，然后从图7所示运动方向运动，发射机与接收机的垂直距离为2 m。实验结果如图8、图9所示。图8为目标静止实验结果，图9为目标运动的实验结果。从图8可以看出，目标静止时的实测结果在AoA方向的估计误差在-7°～7°度之间。

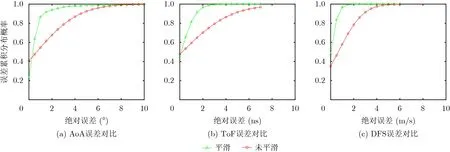
图4 平滑前后的3维参数估计误差对比

图5 不同信噪比下平滑前后的3维参数估计RMSE对比

图6 实验设备图

在数据收发过程中，由于硬件不完善，由NICs测量的CSI会引入采样频率偏移(Sampling Frequency Offset, SFO)、包边界检测(Packet Boundary Detection, PBD)错误、中心频率偏移(Central Frequency Offset, CFO)等误差[17]。对于飞行时间的估计，由于Wi-Fi带宽为40MHz，Wi-Fi设备本身带来的时延估计误差为0.25×10−7s，而信号从发射机发出到达接收机的过程中经历的时延大约为10−8s。因此，由于误差过大不能准确地估计出信号的飞行时间，但是目标静止的时候信号传播的路径相对比较稳定，ToF只有小幅度的波动。而对于目标运动的情况，目标从开始运动到运动结束的这一段时间内，接收机相对于发射机的角度从-50 °～-20 °变化，如图9所示，符合实验场景。目标运动时的ToF比目标静止时的ToF的波动大，且目标运动的ToF在0 ns周围分布有许多较稳定的极值，然后在更大的ToF的地方存在较大的波动，因为发射机开始发送数据包时，目标先静止了2～3 s，然后再开始运动，因此ToF既存在较稳定的部分极值，也存在波动较大的极值，进一步证明了实验的准确性。对于DFS，由于相位是关于2 π的周期函数，当发包速率为500 包/s时，根据相位exp(−j2πFvt/c)计算其周期约为25。由于实验的Wi-Fi设备固有的误差以及实验环境的影响，DFS的估计存在一定的误差，这个误差表现为参数估计结果在DFS方向上的扩展，但是通过实验结果本文发现实验设备以及环境导致的误差使DFS在一个周期内都存在极值，使本文无法仅仅通过DFS分辨出静止目标和运动目标。但是通过AoA, ToF以及DFS的联合估计，本文可以通过运动目标和静止目标极值点的波动情况以及角度的变化情况分辨出静止目标和运动目标，以及目标的运动方向。

图7 实验场景图

图8 目标静止的3维参数估计

图9 目标运动的3维参数估计

将3维参数估计算法与2维参数估计算法进行对比实验。通过前面的误差分析，由于硬件的不完善以及带宽较低等因素的影响，ToF和DFS的估计并不准确，因此，本文分别用2维联合估计算法和3维联合估计算法对AoA, ToF和DFS进行参数估计，但是仅对AoA的参数估计精度进行对比，如图10所示。

从图10可以看出，3维参数估计方法的AoA估计精度高于2维参数估计方法，证明了3维参数估计在参数估计性能上的优越性。其次，3维参数估计较2维参数估计的另外一个优点是3维参数估计的信号分辨能力高于2维参数估计，当入射信号的到达角和飞行时间相近时，2维参数估计无法分辨出参数相近的多个入射信号源的参数，也就不能将信号分开，但是由于3维参数估计较2维参数估计多了多普勒频偏信息，当到达角和飞行时间相近时，可以通过多普勒频偏将多个信号分开，使其对信号的分辨能力提高。

为了证明本文提出的3维联合参数估计算法的优越性，将其与现有的性能优越的参数估计算法进行比较。Widar2.0[14]提出的参数估计算法可以分别估计出AoA, ToF, DFS和信号衰减，且相比于现有的其他参数估计算法有更高的参数估计精度，因此将该参数估计算法与本文提出的参数估计算法进行比较。

用3维联合参数估计算法和Widar2.0中的SAGE算法进行实测验证，同样只提取AoA的参数估计结果进行对比。AoA估计结果如图11所示。

从图11可以看出，在室内场景下，环境中的障碍物增多，障碍物对室内目标信号存在较大的影响，但是本文提出的3维联合参数估计算法对复杂环境中的目标信号的AoA估计误差可以控制在10°以内，而SAGE算法的AoA估计误差为14°左右，其参数估计精度低于3维联合参数估计算法。首先，因为SAGE算法是通过不断地对估计得到参数进行迭代对信号参数进行估计，当初始化参数发生偏差时，该参数估计结果容易陷入局部最优值。其次，SAGE算法是对AoA, ToF, DFS等参数依次进行估计，每一次的参数估计结果都会对后面的参数估计产生影响，且随着室内障碍物的增多，环境干扰增大，叠加的影响也会增大。在复杂的室内环境下，SAGE算法的参数估计精度低于本文提出的3维联合参数估计算法。

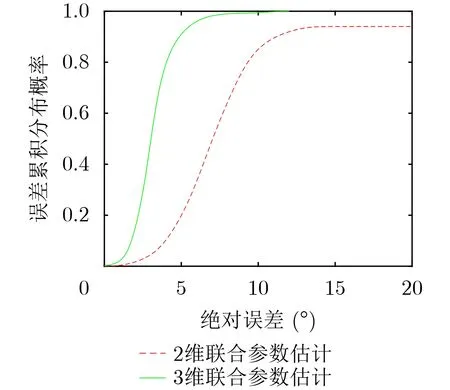
图10 2维和3维参数估计误差累积分布图

4.4 算法复杂度分析与比较

本文提出的3维联合参数估计算法相比于现有的基于最大似然估计的3维参数估计算法，对参数的估计精度得到了提高，但是由于增加了搜索维度，其时间复杂度也增大了很多。两个算法的时间复杂度和天线个数、子载波个数、估计1次的数据包个数、参数搜索范围和步长、平滑窗大小以及待估计的信号个数相关。在实际测量的过程中，天线数、子载波数、数据包个数固定不变。3维联合参数估计算法的平滑窗长度固定。AoA, ToF和DFS的搜索范围和搜索步长共同决定了参数搜索长度。假设AoA, ToF和DFS的搜索长度分别为length_aoa,length_tof, length_dfs，则3维联合参数估计算法的时间复杂度(实数乘)为length_aoa×length_tof×length_dfs×(MNP/8)2，SAGE算法进行参数估计的时间复杂度(实数乘)为(length_aoa×NP+length_tof×MP+length_dfs×MN)，为了能够捕捉到室内环境中的多径信号，AoA, ToF和DFS的搜索范围均在能够包括所有信号的最小范围内，则搜索长度由3个参数的搜索步长决定。本文提出的3维联合估计算法和SAGE算法在不同的搜索长度和待估计信号个数下的时间复杂度如图12所示。

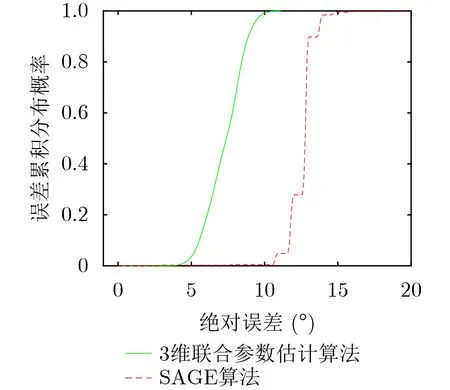
图11 室内场景AoA估计精度对比

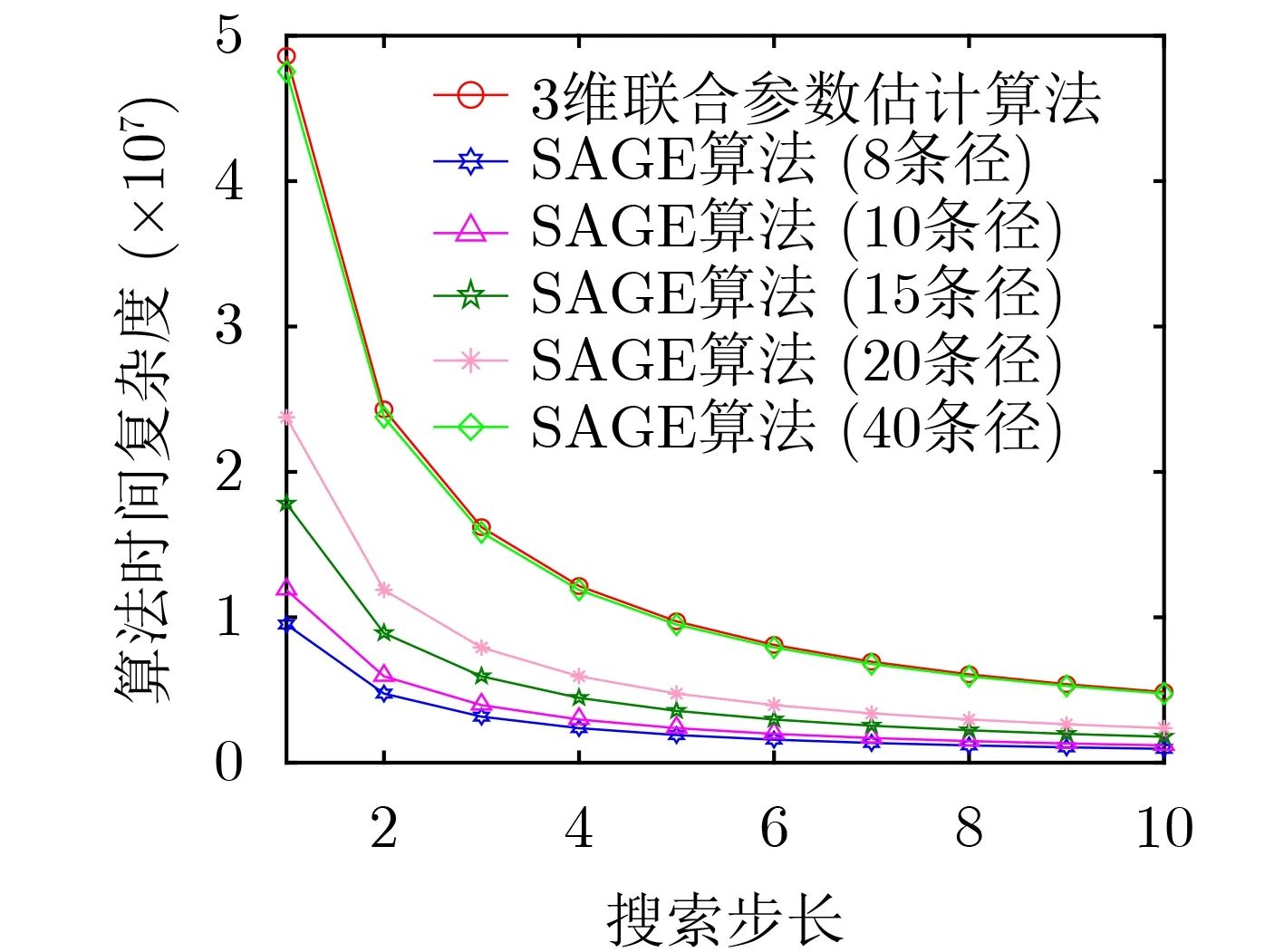
图12 两种算法时间复杂度比较

从图12可以看出，3维联合参数估计算法由于需要对3个维度的参数进行遍历，其算法时间复杂度较高，在室内多径数较少时，SAGE算法的时间复杂度比本文提出的3维联合估计算法低。随着待估计信号个数的增多，SAGE算法时间复杂度略有上升。一般情况下，室内环境的多径数在9～12条，此时SAGE算法的时间复杂度低于3维联合参数估计算法。当室内环境变得更加复杂，多径数大于40条的时候，SAGE算法的时间复杂度超过了3维联合估计算法。因此，本文提出的3维联合参数估计算法在时间复杂度方面和现有的参数估计算法相比较高，但在参数估计精度上优于现有的参数估计算法。对于复杂环境下的非时延敏感性业务，具有明显的优势。随着硬件设备计算能力的提升，本文所提算法的优越性将更加突出。

5 结束语

本文提出了一种基于CSI的3维参数联合估计算法，该方法在1维参数估计和2维联合参数估计的基础上加入了多普勒频偏信息，使得在仅有3根天线的情况下可以同时完成AoA, ToF和DFS的估计，解决了2维参数估计不能分辨到达角和时延相近的多个信号源的问题，提高了信号参数估计精度和信号的分辨能力。与基于最大似然估计的3维参数估计算法相比，本算法避免了参数估计的局部收敛问题，其参数估计精度更高。同时，基于实际环境中的信号之间具有强的相干性，而相干信号由于其协方差矩阵不是满秩矩阵而不能直接使用MUSIC算法对其进行参数估计的特点，提出了3维空间平滑算法，以去除相干信号对参数估计的影响。但是由于实际环境的干扰以及实验设备的限制，DFS和ToF的估计存在较大的误差，如何消除实验过程中环境或者设备对DFS估计的影响以及减小算法时间复杂度将会是下一步工作的重点。