融合多权重因素的低秩概率矩阵分解推荐模型

王 丹 田广强 王福忠

①(黄河交通学院智能工程学院 焦作 454950)

②(河南理工大学电气工程与自动化学院 焦作 454000)

1 引 言

2 多上下文特征信息

2.1 用户间信任度

给定用户u ∈U，活动s ∈S，用户间的信任分为直接信任和间接信任。所谓直接信任只涉及用户两者，而间接信任会牵扯第三者。用户间的信任度越接近1，表明两者之间越信任，反之亦然。在社交网络中，用户被信任的人数越多表明用户的可信度越高。本文借助Page rank算法构建用户直接信任度

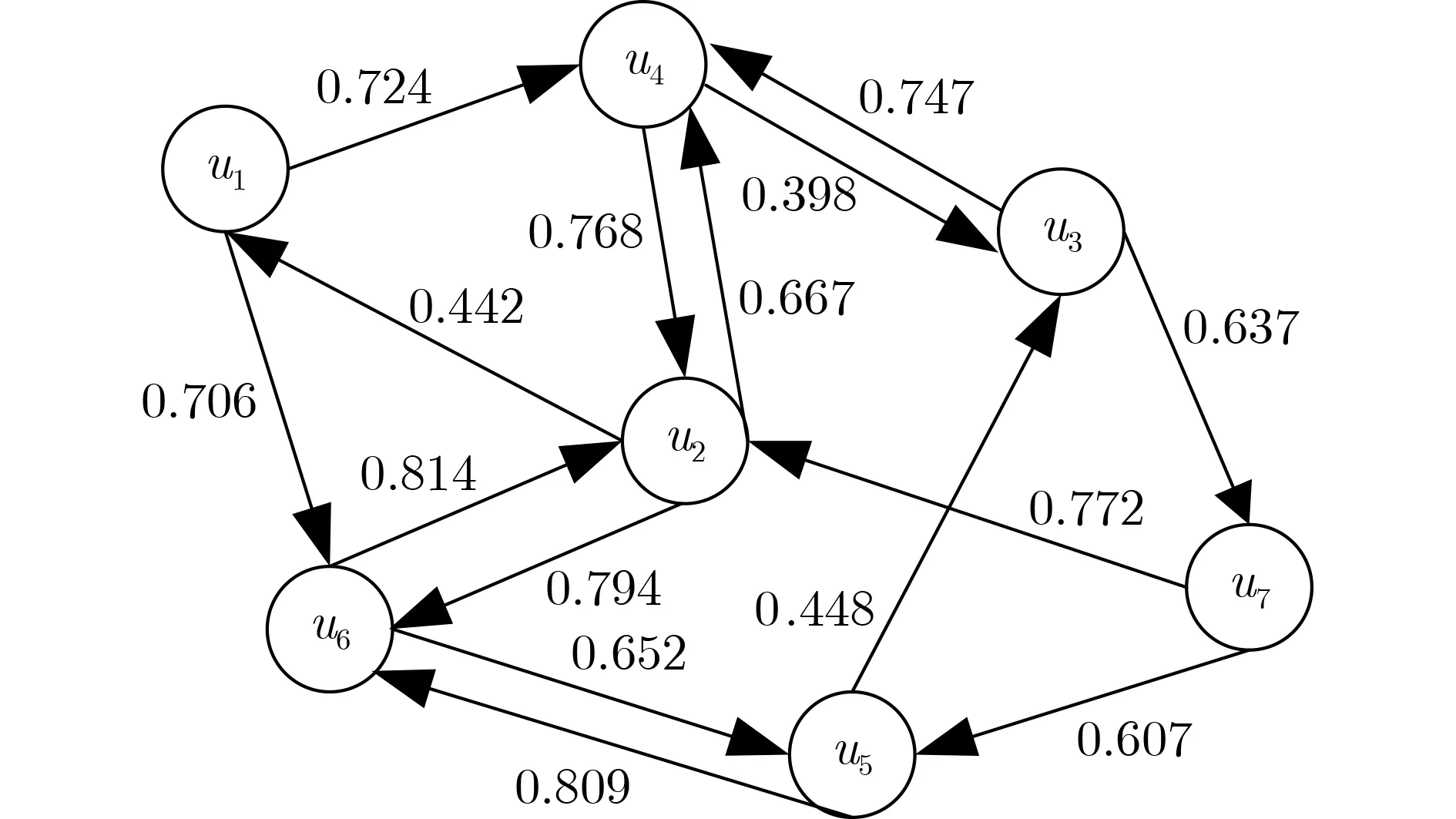
图1 信任网络

2.2 用户社会地位影响力

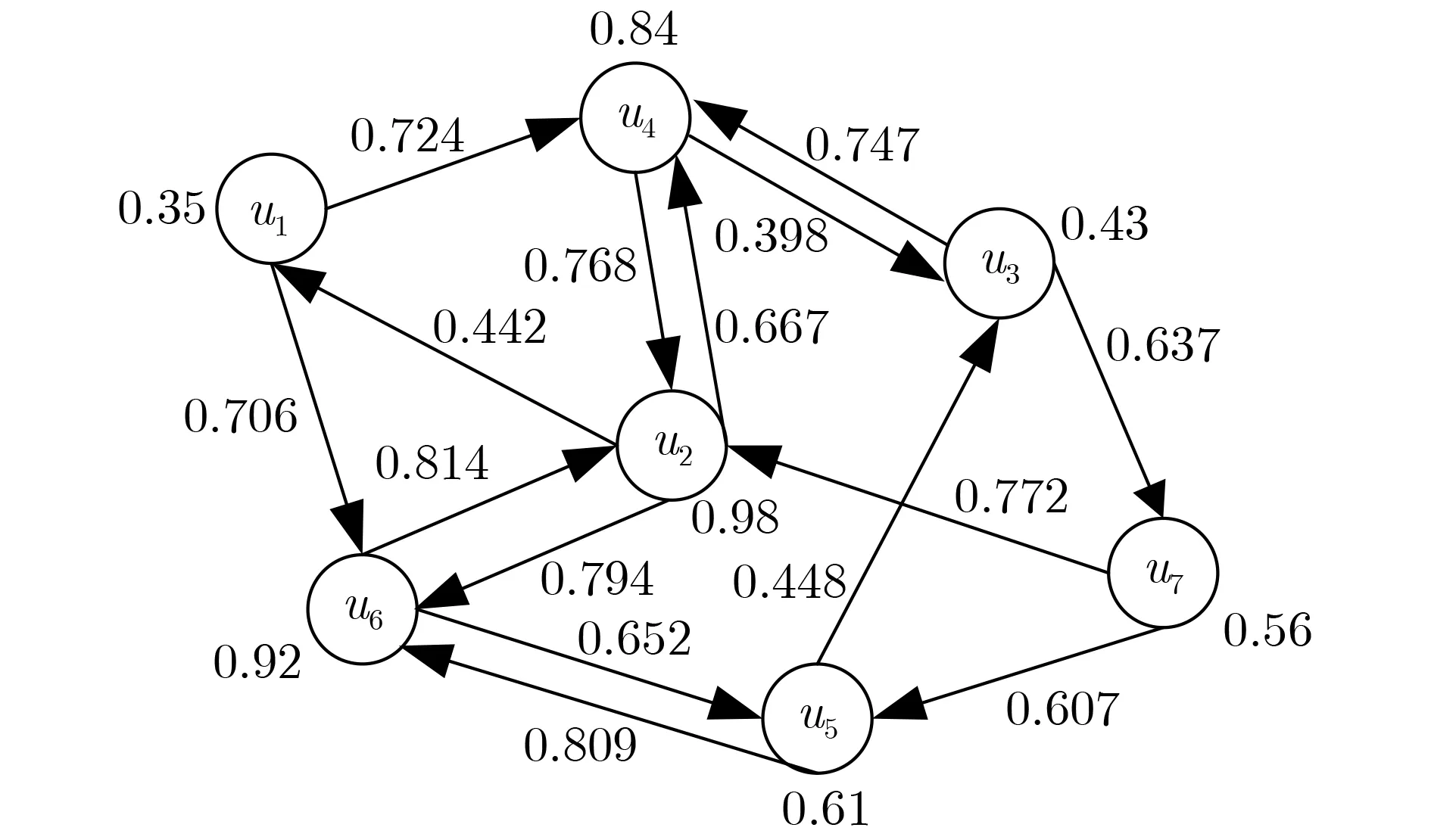
图2 具有社会地位影响力的信任网络

2.3 用户同质性

3 融合多权重因素的矩阵分解

3.1 低秩概率矩阵分解

基于矩阵分解的协同过滤模型具有良好的可扩展性和推荐精度，得到了越来越多的关注和研究。这里采用低秩概率矩阵分解(Probabilistic Matrix Factorization, PMF)作为本文推荐的框架，利用该框架对用户-活动评分矩阵进行分解，将用户偏好和活动特征映射到同一潜在低秩空间中，然后利用低秩特征矩阵对用户评分缺失进行预测。

3.2 融合信任关系

综上分析了用户间的信任度、用户社会地位影响力以及用户的同质性，本文将这些权重因素融入矩阵分解中。图3为融合用户间信任关系的矩阵分解示意图。

3.3 融合用户社会影响度

根据文献[14]，假设用户和活动的隐特征向量服从高斯先验分布

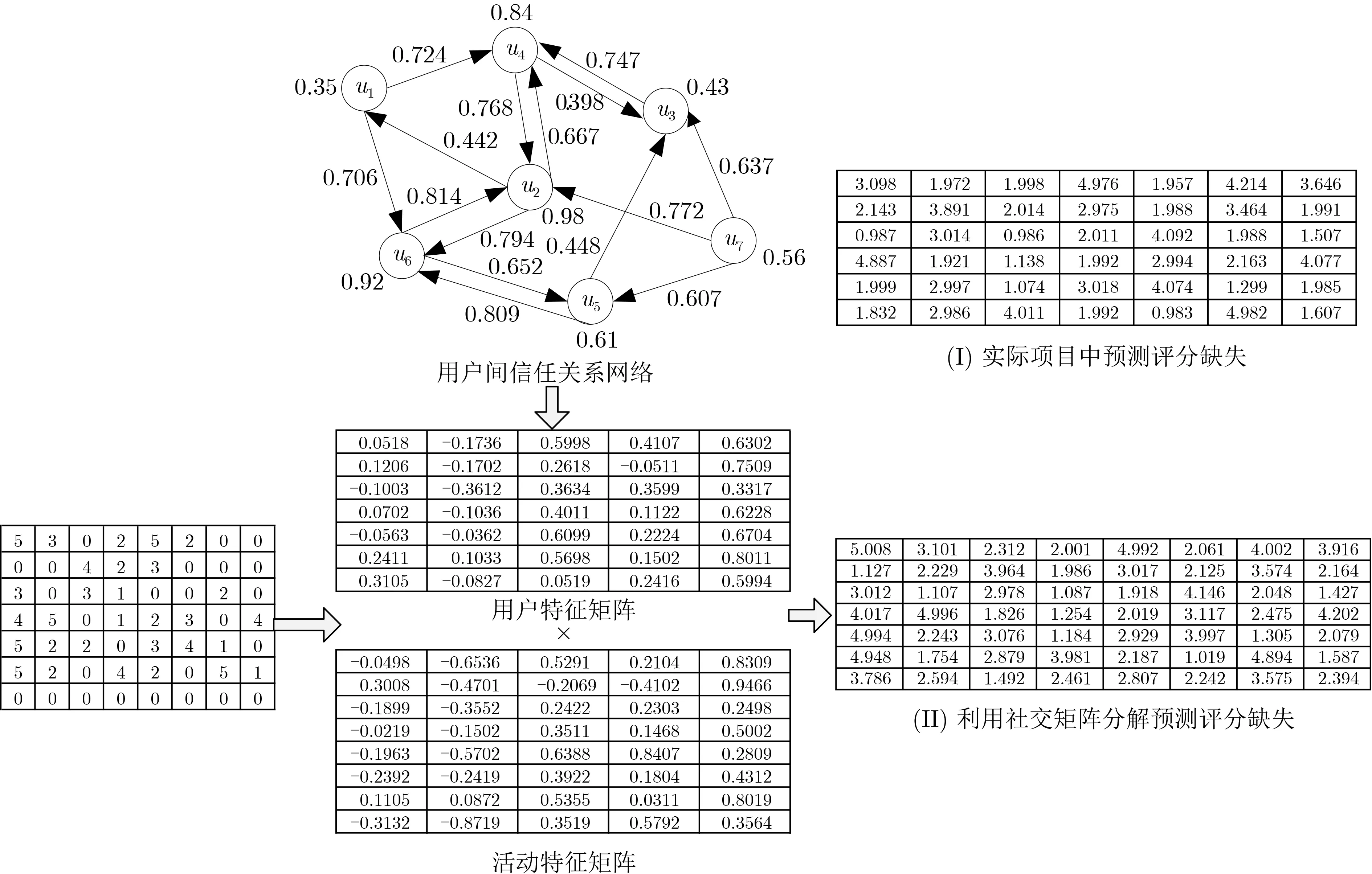
图3 矩阵分解示意图

3.4 融合用户同质性

3.5 本文算法

4 仿真实验与对比分析

4.1 实验数据及评价标准

本文算法目的是为某个城市中的用户推荐感兴趣的活动或项目，为了验证本文算法的有效性和优越性，以豆瓣和Ciao为实验数据来源。在豆瓣上选择北京市2018年1月1日～2019年12月31日期间用户评价的活动或项目为实验数据，豆瓣用户可以对自己所感兴趣的书籍、电影、电视剧、音乐进行评价，其中在北京数据集上共有15384名用户，相互信任关系141556条，产生的有效评分70146条，评分信息的稀疏度为98.32%，用户社交关系的稀疏度为99.88%。

Ciao是著名的欧洲消费点评网站，网站用户不仅可以浏览其他用户的评论还可以对其参与的商品进行评价。本文所采用的实验数据来自Tang等人[15]获取的1999年～2011年间的项目评分和社交数据。其中共有7357名用户，评分记录278483条，相互信任关系111781条，评分信息的稀疏度为99.96%，用户社交关系的稀疏度为99.59%。

平均绝对误差(Mean Absolute Error, MAE)和均方差误差(Root Mean Squared Error, RMSE)是目前推荐领域最为常见评价方法

心理学表明，少年儿童的好奇心强，容易对周围陌生的事物产生浓厚的兴趣，由于儿童的阅历浅、头脑中的疑问较多，爱问“为什么”因此，科学课教师要根据一般儿童的年龄和心理特点，尤其要了解所教学生的情况和特点，不能吝啬自己的语言，而应用赞美的话调动学生，用鼓励的话语使学生感到兴奋，精心设计出学生喜爱科学探究活动，引领学生踏上科学探究学习之路。

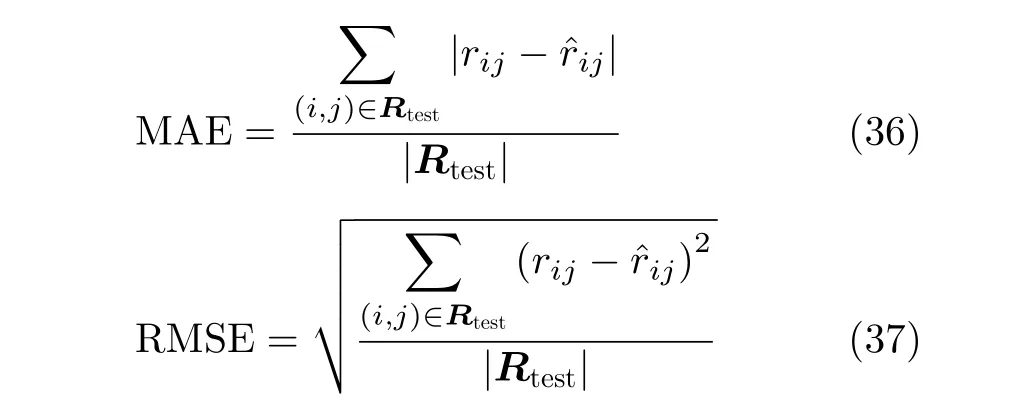
参考文献[16-20]对文中的参数设定如表1所示。

4.2 参数设置

用户社会影响力和同质性是影响推荐的重要因素，参数λW,λH大小决定着用户行为和地位对信任用户的渗透力。这里在豆瓣北京和Ciao数据集上测试参数λW,λH与推荐评价指标MAE间的关系。当其他调节参数设置为0时，社会影响力调节参数λW与平均绝对误差MAE的关系如图4所示。

由图4可知，在豆瓣北京和Ciao数据集上随着参数λW的增大，推荐评价指标MAE值先降后增。并且训练数据越多，得到的推荐精度就越高,预测误差就越小。在豆瓣北京数据集上λW=5时MAE取得最小值，算法此时获得最好的预测结果；在Ciao数据集上λW=4时MAE取得最小值，综上所述，本文将用户社会影响力调节参数λW设置为5。当其他调节参数设置为0时，同质性调节参数λH与平均绝对误差MAE的关系如下。

由图5可以看出，在豆瓣北京和Ciao数据集上参数λH与MAE的变化趋势是一致的，即随着λH的不断增大，平均绝对误差MAE先下降后增大。并且随着训练数据的增多，平均绝对误差MAE越小，推荐预测精度越高。在豆瓣北京数据集上λH=0.35时平均绝对误差MAE取得最小值；在Ciao数据集上λH=0.7时MAE取得最小值。为了使获得的推荐精度最优，我们这里折中取值λH=0.5，虽然此时在不同的数据集上不能获得最优结果，但能获得平均最优。

为了降低偏差对预测精度的影响，本文引入两个正则项分别对用户特征和活动特征进行约束，约束参数φ和φ分别用于控制用户特征和活动特征受近邻的影响程度。图6和图7分别为正则项约束参数φ和φ与平均绝对误差MAE间的关系。

由图6可知，在豆瓣北京数据集上，随着用户特征正则项约束参数φ的增大，平均绝对误差MAE大致的走势是先降低后增大，在0.05≤φ ≤0.08之间，平均绝对误差MAE振荡上升；在Ciao数据集上，随着用户特征正则项约束参数φ的增大，平均绝对误差MAE也是先降低后增大。并且随着训练数据的增多，平均绝对误差MAE越小，算法的推荐预测精度越高。在豆瓣北京数据集上时正则项约束参数φ=0.048时平均绝对误差MAE取得最小值；在Ciao数据集上正则项约束参数φ=0.03时MAE取得最小值。综合取用户特征正则项约束参数φ=0.048。

表1 参数设置

图4 不同数据集上参数λW与MAE关系

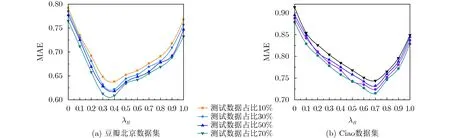
图5 不同数据集上参数λ H与MAE关系

图7为豆瓣北京和Ciao数据集上，活动特征正则项约束参数φ与平均绝对误差MAE间的关系。随着正则项约束参数φ取值的增大，平均绝对误差MAE呈“W”状波动变化。在豆瓣北京数据集上当φ=0.1时平均绝对误差MAE取得最小值；在Ciao数据集上，正则项约束参数φ=0.102时，平均绝对误差MAE取得最小值。并且随着训练数据的增多，平均绝对误差MAE越小，算法的推荐预测精度越高。综合取用户特征正则项约束参数φ=0.01。上述两个正则项约束参数既不能取值太大，也不能取值太小，取值太大则会控制学习的进度，取值太小就无法起到约束的作用。

隐特征矩阵维度d也是影响算法性能的因素之一，维度太大可表征的隐藏信息就越多，但引入噪声信息的可能也越大，若维度太小，就无法全面挖掘深层隐藏信息，为此选择恰当的维度至关重要。

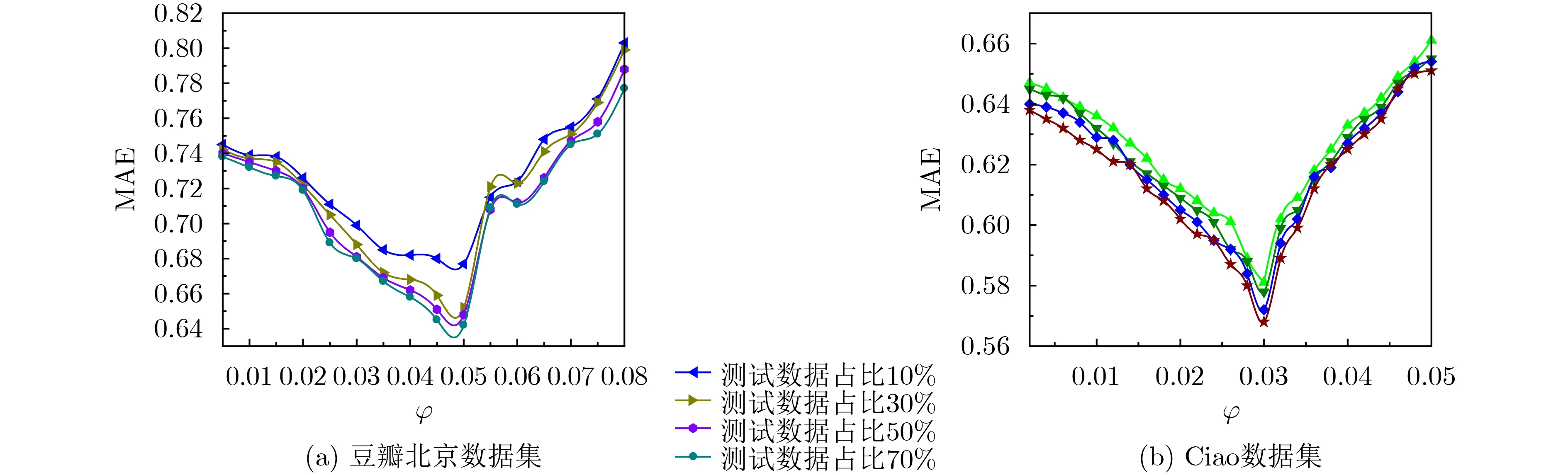
图6 不同数据集上参数φ 与MAE关系

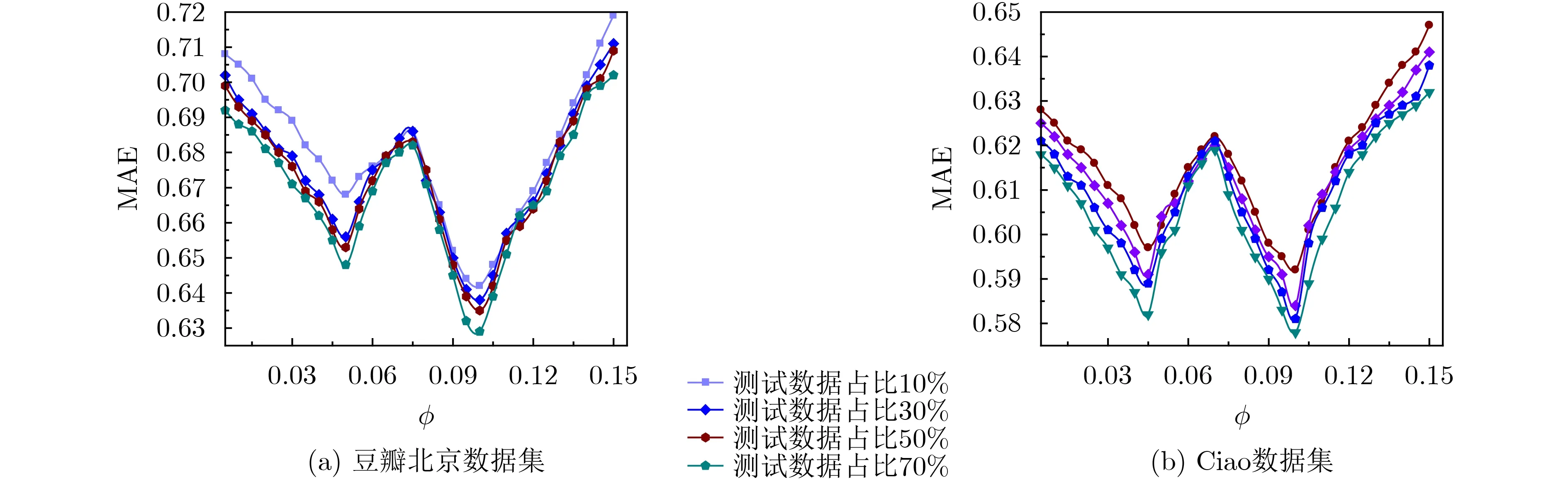
图7 不同数据集上参数φ 与MAE关系

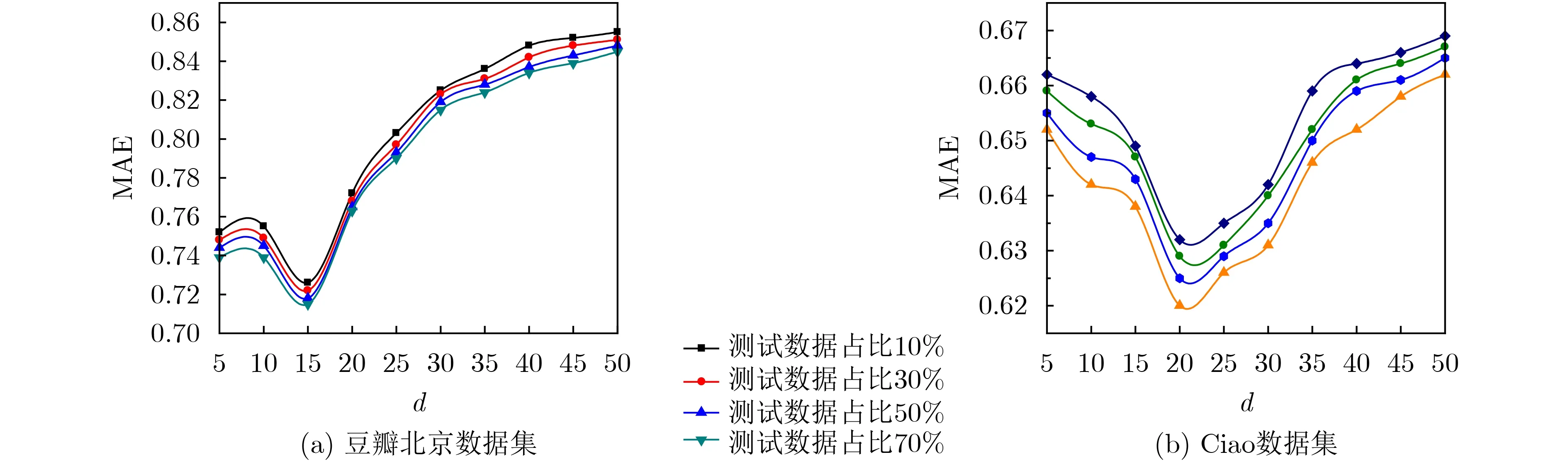
图8 不同数据集上维度d 与MAE关系

从图8曲线走势可知，在豆瓣北京数据集上，随着隐特征矩阵维度d的增大，平均绝对误差MAE先降低后增大后期增幅缓慢，其中维度d=15时，平均绝对误差MAE取得最小值；在Ciao数据集上，随着隐特征矩阵维度d的增大，平均绝对误差MAE先降低后缓慢增加，其中维度d=20时，平均绝对误差MAE取得最小值。无论在豆瓣北京数据集上还是在Ciao数据集上，当隐特征矩阵维度大于一定阈值后，不仅不会降低平均绝对误差，反而缓慢增加，这也侧面反映出隐含特征所能表达的信息是有限的，徒增特征矩阵的维度，不仅不能提升推荐的准确率，反而会引入一些不必要的噪声，降低推荐的精度。

本文仿真实验的硬件环境为:I n t e l(R)Core(TM) i5-9400F@4.1 GHz, RAM: 4 GB，软件环境为：Windows 7操作系统，Python编程实现。对比实验从两个方面进行：一是对比分析各算法的有效性；二是对比本算法与同类算法对冷启动的敏感性。实验采用八折交叉验证，即将每3个月的活动数据作为子数据集，这样的数据划分主要考虑到同一季度内由于气候和环境的相似，活动项目能聚类出现。

这里将文献[1 7](M I M F C F)、文献[1 2](ISSMF)、文献[19](CSIT)、文献[21](RSNMF)、文献[22](PMF)、文献[23](AODR)、文献[24](CANCF)和文献[25](AutoTrustRec)作为对比算法，MIMFCF,ISSMF,CSIT,RSNMF和PMF等5种算法为传统推荐算法，AODR, CA-NCF, AutoTrustRec等3种为深度学习推荐模型。其中MIMFCF提出了两个有效矩阵分解框架，一个集成流形正则化，一个集成动态Tikhonov图正则化；基于二者深入挖掘用户-项目矩阵的内在信息；ISSMF利用整体社交网络结构信息和用户的评分信息推导特定领域社交网络结构,借助Pagerank计算用户在特定领域的社会地位，并将其融入矩阵分解；CSIT将用户信任朋友的影响引入矩阵分解模型中，借助聚类舒缓数据稀疏问题；RSNMF为基于正则项约束的非负矩阵分解算法；AODR使用深度学习从评论文本提取评分矩阵，引入张量因子分解计算加权意见，然后融合扩展协作过滤技术改进推进系统；CA-NCF提出了一种混合算法来追溯和重新利用预筛选上下文信息，并将获得的新维度用于深度学习协作过滤；AutoTrustRec利用深度架构来学习隐藏的用户和项目表示，使用自动编码器中的共享层将直接和间接信任值反馈神经网络。

4.3 算法的有效性

为了进一步验证本文算法与其他同类算法的有效性，以平均绝对误差MAE和均方差误差RMSE作为评价标准，分别在豆瓣北京和Ciao数据集上进行对比实验，结果如图9所示。

从图9(a)上可以看出，当确定特征维度时，本文算法(MWFPMF)的平均绝对误差是最低的，其次是CSIT, MIMFCF, RSNMF, ISSMF和PMF；特别当特征维度d=15时，本文算法的平均绝对误差MAE取得最小值，至少低于其他5种算法8.24%，此时获得的推荐精度最佳。当增加特征维度，即d=20时各算法的平均绝对误差不仅没有降低，反而增大了，这是由于随着特征维度的增加，其能表达的隐含特征信息加大，无形中引入了噪声，反而降低了算法推荐的准确率。图9(b)中可知，在Ciao数据集上随着特征维度的增大，各算法的推荐准确率在提升，当特征维度d=20时，各算法推荐精度达到最高值，此时本文算法的平均绝对误差至少低于其他5种算法6.58%。

图10的变化趋势与图9基本一致，从图10(a)可知：在确定维度上，本文算法的均方差误差相较于其他5种算法是最低的，其中当特征维度d=15时，本文算法的均方差误差RMSE取得最小值，至少低于其他5种算法7.83%，所得到的推荐精度最高；图10(b)中可知，在Ciao数据集上随着特征维度的增大，各算法的均方差误差RMSE在降低，当特征维度d=20时，各算法的均方差误差达到最小值，此时本文算法的均方差误差至少低于其他5种算法6.27%。

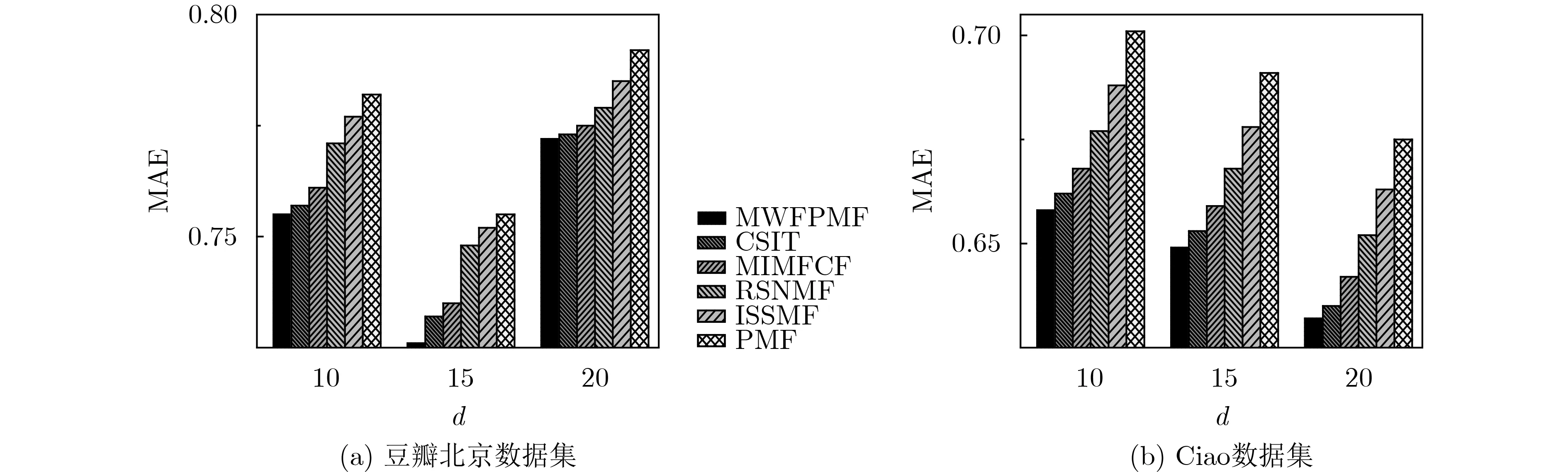
图9 不同数据集上维度d 与MAE关系

4.4 冷启动用户对算法性能影响

为了进一步验证本算法对冷启动用户推荐的精度，这里将用户评分项目少于3个归为冷启动用户，分别从豆瓣北京和Ciao数据集上抽取冷启动用户，以平均绝对误差MAE和均方差误差RMSE作为推荐评价标准，验证各算法对冷启动用户的推荐性能。

通过表2推荐评价指标对比可知，在豆瓣北京数据集上本文算法对冷启动用户推荐的平均绝对误差相较于CSIT, MIMFCF, RSNMF, ISSMF,PMF等5种传统推荐算法分别降低了5.64%, 8.92%,11.07%, 20.02%和22.05%，相较于AODR, CANCF, AutoTrustRec等3种深度学习推荐模型平均绝对误差分别仅降低了0.9%, 2.82%和6.78%；对冷启动用户推荐的均方差误差相较于CSIT, MIMFCF, RSNMF, ISSMF, PMF等5种传统推荐算法分别降低了8.08%, 10.55%, 13.41%, 20.19%和24.27%，相较于AODR, CA-NCF, Auto-TrustRec等3种深度学习推荐模型均方差误差分别仅降低了3.01%, 4.02%和8.61%。

在Ciao数据集上本文算法对冷启动用户推荐的平均绝对误差相较于CSIT, MIMFCF, RSNMF,ISSMF, PMF等5种传统推荐算法分别降低了7.34%, 9.51%, 12.42%, 19.15%和22.03%，相较于AODR, CA-NCF, AutoTrustRec等3种深度学习推荐模型平均绝对误差分别仅降低了0.89%, 2.45%和7.57%；对冷启动用户推荐的均方差误差相较于CSIT, MIMFCF, RSNMF, ISSMF, PMF等5种传统推荐算法分别降低了8.52%, 9.58%, 15.52%,22.69%和26.56%，相较于AODR, CA-NCF, Auto-TrustRec等3种深度学习推荐模型均方差误差分别仅降低了3.35%, 4.5%和9.11%。

通过以上对比可知，传统矩阵分解推荐模型PMF, ISSMF和RSNMF效果较差，这是由于传统模型仅依赖用户对活动项目的评分并没有充分利用用户间信任去拓展分析信任用户间的兴趣偏好，面对稀疏数据，无法进一步提高推荐的精准性；推荐模型CSIT和MIMFCF的推荐性能较传统矩阵分解推荐模型PMF, ISSMF, RSNMF有较大的提升，这是因为它们集成了1种或多种社交关系到矩阵分解中，通过深入挖掘信任用户间的隐含关联，以求准确获取目标用户的兴趣偏好，一定程度上提高了推荐的精准度。AODR, CA-NCF和AutoTrustRec 3种深度学习推荐算法从不同角度借助深度学习挖掘有限的用户评论信息，同时融合加权意见, 上下文信息等手段进一步提高了推荐精准度，相比其他5种传统算法推荐精度有一定提高，但本文对冷启动用户融合多权重因素借助低秩概率矩阵进行深入分解，隐匿关联信息的挖掘更为充分，推荐性能更为优异。

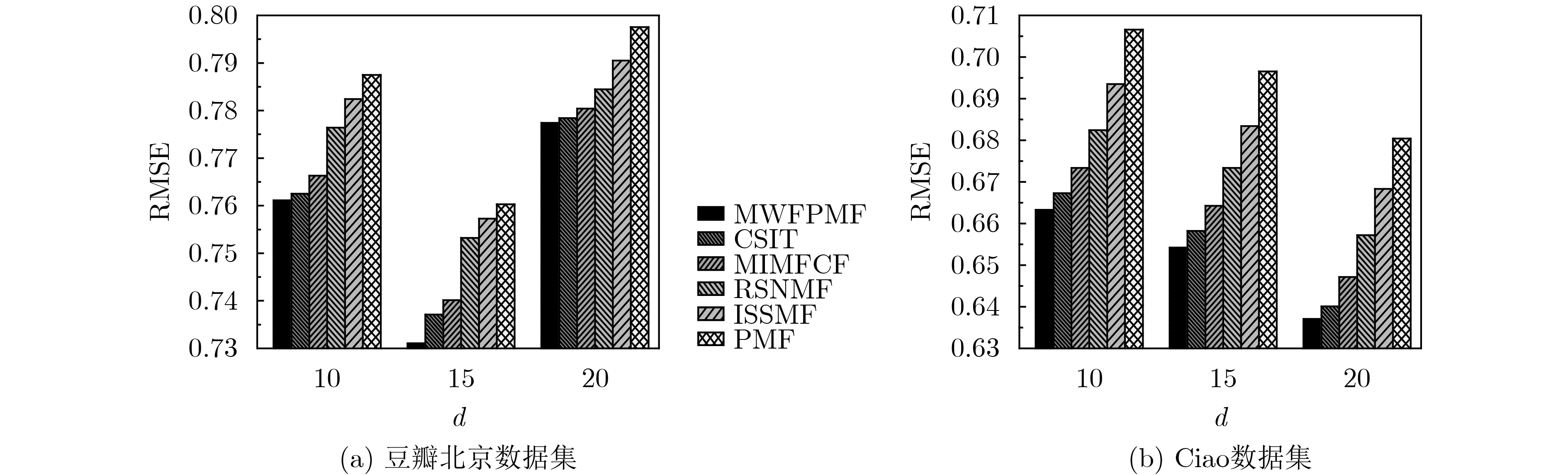
图10 不同数据集上维度d 与RMSE关系

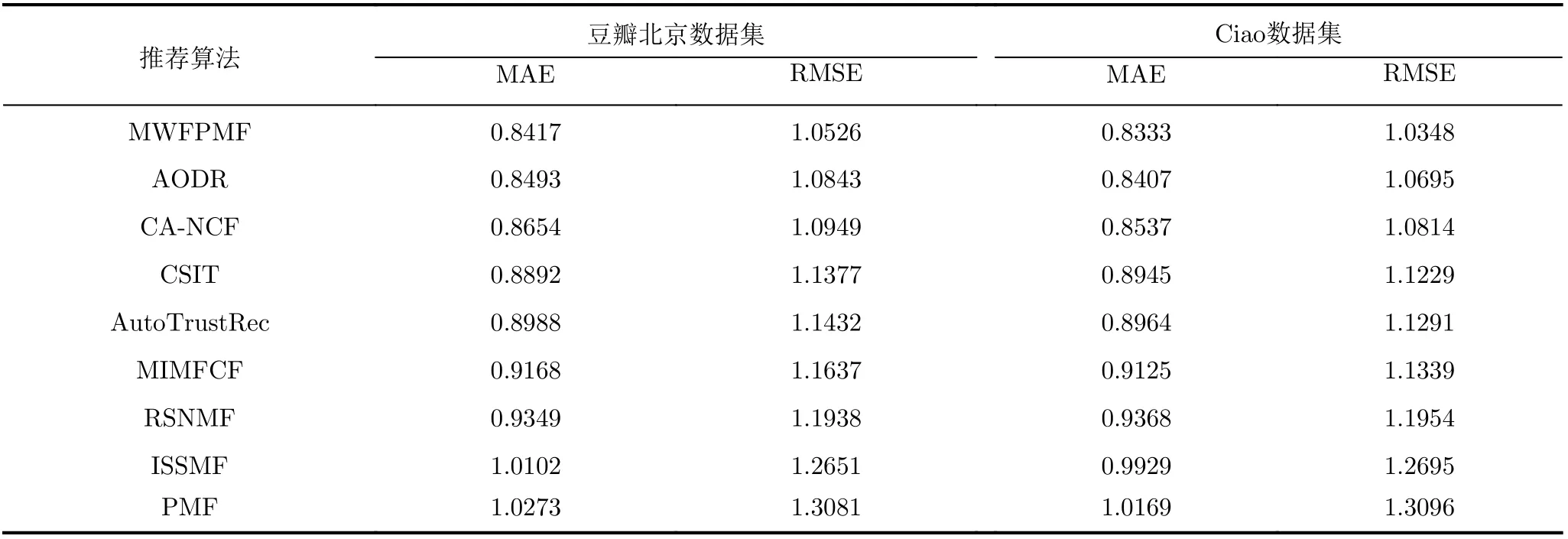
表2 各算法对冷启动用户的推荐性能比较

4.5 数据量对算法性能的影响

为了进一步对比分析传统推荐算法与深度学习推荐模型的性能，这里分别取豆瓣北京和Ciao数据集1%, 50%和100%的数据量进行测试。由于1%的数据量偏少，为了充分利用有限数据，防止过拟合，在1%数据集上采用5折交叉验证，而50%和100%数据集上随机选择80%的数据用于训练，剩余20%用作测试。以平均绝对误差MAE和均方差误差RMSE作为评价标准，结果如下：

由于图11和图12可以得出，数据集测试比例逐渐增大时，各算法推荐的平均绝对误差MAE和均方差误差RMSE随之降低，表明算法的推荐精度在提高。在豆瓣北京数据集上，本文算法推荐的平均绝对误差MAE和均方差误差RMSE都低于CSIT,MIMFCF, RSNMF, ISSMF, PMF等5种传统推荐算法，推荐精度明显高于5种传统推荐算法；与AODR, CA-NCF, AutoTrustRec等3种深度学习推荐模型相比，本文算法在数据集比例较低时(1%数据量)，平均绝对误差MAE和均方差误差RMSE均低于3种深度学习推荐模型，表现出了优秀的推荐效果，这是由于本文推荐算法融合用户间信任度、用户社会地位影响力和用户同质性等多权重因素，借助低秩概率矩阵分解对用户-活动进行了深入充分的挖掘，在有限测试数据量下一定程度上提高了推荐精度。随着测试数据集比例的增大，3种深度学习推荐模型的推荐精度提升较快，当以全部数据测试推荐时，AODR推荐算法的平均绝对误差MAE与本文算法接近。

在Ciao数据集上获得的结果与在豆瓣北京数据集上基本一致，但在以全部数据测试推荐时，AODR推荐算法的平均绝对误差MAE和均方差误差RMSE略低于本文推荐算法。综上可知本文推荐算法较适用于冷启动或数据量较小的推荐场合。

5 结束语

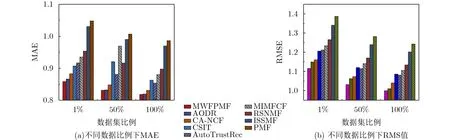
图11 豆瓣北京数据集上各算法评价指标

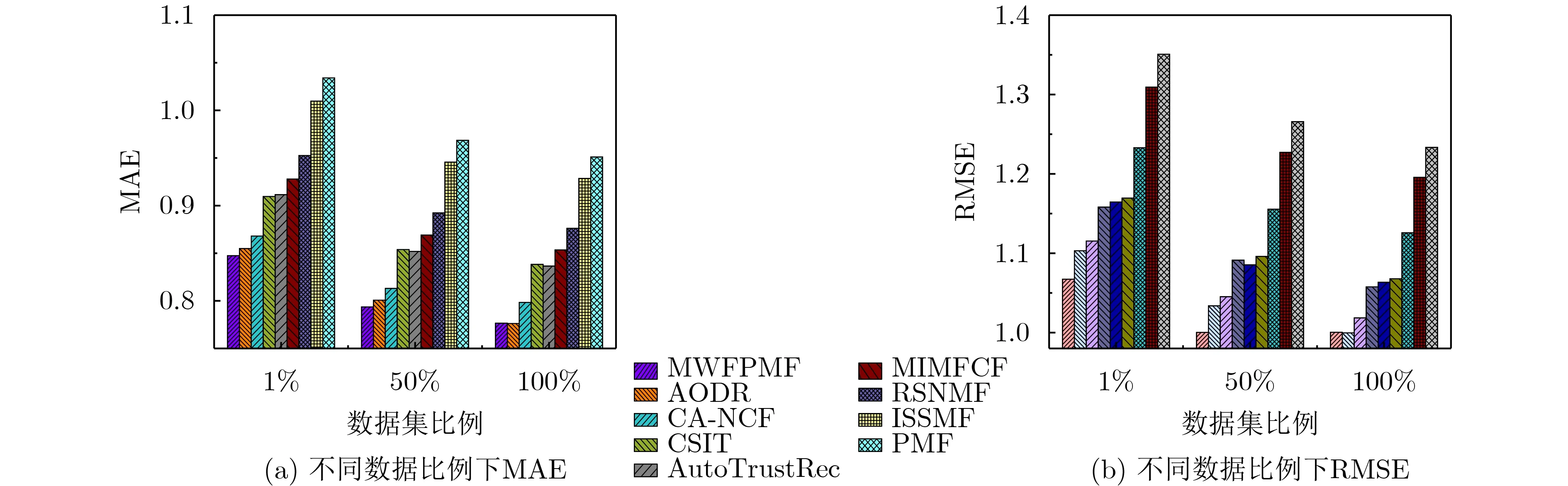
图12 Ciao数据集上各算法评价指标

用户间的信任度、同质性以及在一定范围内的影响力会影响其他用户的决策。本文从社会认知理论着手，将用户间信任度、用户社会地位影响力和用户同质性3因素融入低秩概率矩阵分解中，构建多权重因素的低秩概率矩阵分解推荐模型。本文推荐模型不仅对一般用户有较高的推荐精度，冷启动用户也取得了不错的结果。在现实生活中，用户间的信任、同质性以及社会影响力会随着时间变化而变化，如何随时更新多属性权重，融入深度学习模型中，将是文章下一步的研究重点。