直升机场建设过程中方格网法土方量计算模型研究

陶彬 夏露 王思扬

（中国人民解放军陆军航空兵学院,北京 101116）

土方量是机场选址建设阶段必须考虑因素。选堪阶段,通过在地形图上快速测定直升机场预设地域的土方量,能够快速确定直升机场的工程进度,方便指挥员指挥重型工程机械开展机场场址建设作业,为指挥决策提供准确数据。在工程项目上,精确的土方量计算直接影响场址建设进度,有时还会引起相关各方的经济纠纷。本文针对直升机场开辟过程中对场地的整平要求,开展土方量计算研究,设计直升机场开辟过程中的土方量计算模型。基于Matlab/Simulink 数字化建模软件,对土方量计算模型进行建模,实现土方量的快速运算。

1 直升机场对地势的要求

直升机场有一定的跑道长度、停机坪数量,平整度是场道表面评价的一个重要参数。不同等级的直升机场场道平面都有严格标准,而实际建设中存在一定的偏差,我们把这种偏差叫做平整度。平整度非常关键直接影响直升机的滑行动力、跑道承受力,因而直接影响飞行质量。在机场建设管理中,用机场跑道面上的凹凸部分表征场道的不平整度。而地势的整平对场道平整度建设有直接联系,因此,良好的平整度需要精准的地势整平作业,精准的土方量计算。

1.1 直升机场平整度要求

为了满足飞机的使用要求,水泥混凝土道面平整度允许值是有一定的上限的。在实际操作中,采用直尺法来衡量平整度,在一定范围内,通过直尺与地面的间隙来确定平整度。因此,专用的场道直尺就是测量工具,根据有无支脚,工具可以划分为两种,有支脚、无支脚,根据长度划分,市面上有3m、4m、5m 等不同规格,我国民用机场等场所测量平整度普遍采用3m 长的直尺。

直升机场平整度要求,如下：

1.1.1 在水泥混凝土到面上,3m 长的测量尺与测定区域接触部位,中间空隙值长度在3mm 以内。在500m 的范围中,检查区域不少于2 块水泥混凝土道面板。水泥混凝土道面需要测量两块水泥板对角线,然后取2 组对角线的间隙的最大值然后进行平均,作为测量值。

1.1.2 高差允许值,相邻两块水泥板纵向连接处的高差值在3mm 以内,横向连接处的高差值在2mm 范围内。纵向缝隙需要在50m 范围内至少检查1 点,横向缝隙需要每10条抽查检验1 条,再检查点的数量上,要求1～2 点。

1.1.3 单块水泥混凝土板设计与实际安装偏差在±5mm范围内。

1.1.4 坡度标准,以直升机轴线方向为标准,为起落坪、停机坪垂直于标准方向的坡度在1.5%范围内,平行于标准方向的坡度在0.8%范围内,在平行、垂直方向上,要确保一个方向的坡度不小于0.5%,同时要满足净空环境以及其他要求。

1.2 保障场地对地势平整度的要求

直升机场保障场地,主要承受各种工程车辆行驶、承载作用。保障场地的平整度直接影响保障车辆的行驶效率、质量。不平整的保障场地会增大行车阻力、迫使保障车辆振动,影响行车的速度和安全,影响驾驶的平稳,增加对保障场地路面冲击和汽车机件的损坏等一系列不良影响.另外,不平整的保障场地还会引发保障场地大面积积水,从而引发保障场地出现塌方等损害。因此,为减少上述灾害、损害的发生,要严格要求保障场地的平整度问题。在地势整平过程中参照直升机场平整度标准,开展整平工作。

2 直升机场土方量计算方法选择

直升机场地面平坦或起伏较小的一个较大区域,其最主要特点就是平坦宽广,起伏较小。实际上,直升机场开设的区域,一般较为平坦,微地貌相对简单,但是地面常常会出现起伏,在区域范围内高差在1m 左右,有机场建设区域地形地势限制,一般在此区域内一般没有等高线。

而方格网法其基本原理是找到等高线,在机场建设区域,进行划分网格,针对划分的网格分别测量出每个网格中各个典型代表点的高程,然后估算出内个网格的平均高程。根据机场各个网格平均高程和机场规划场道要求坡度,确定机场建设区域的填土区域和挖土区域,进一步确定填挖边界线。机场建设区面积也符合网格法对测量面积的需要。应用方格网法开展机场建设土方量计算具有简明直观、通用性强,土方量预算相对准确等特点。

2.1 方格网法土方量计算研究

方格网法将要土方量计算区域划分网格,根据要设计高程以及该区域实际位置高程确定土方的填挖量,最后将填、挖方量累计求和。该方法首先利用方格的四个角的高程求出该方格的平均高程,然后依据设计高程,计算出差值,进而得到此方格的土方量填、挖量,总的土方量等于各方格土方量的和：

式中：Hij表示第i 行j 列的方格网的高差；a,b为方格网边长；n 为测区方格的个数。

2.2 方格网法计算案例分析

2.2.1 打方格网

打方格网是方格网法的关键,首先确定方格的长度,一般取10m、20m、50m 的长度作为基准。其大小要以实际计算土方量的地形复杂程度、比例尺的精度等因素来确定。每个方格点的地面高程可以根据比例尺地形图图上作业求得,标注在图上。（如图1 所示）,本文所选取案例取方格边长20m。

图1 方格网法计算原理图

2.2.2 计算设计高程

每个方格网的高程根据四个顶点的高程求平均值得到。按照此种方法进行递推,再根据方格数,把所有求得的方格平均高程求和,再除以方格的数量,这就是设计高程。

式中Hi为每一方格的平均高程；n 为方格总数。

根据我们计算出来的设计高程的值与每个方格计算的高程值进行比较、计算,分别确定出每个方格的填、挖土方量的值。从求解过程,可以看出网格法求土方量计算工作较大。

通过对土方量设计高程计算过程的研究可以看出：角点A1、A4、B5、E1、E5的高程在计算过程中只是使用过1 次,边点A2、A3、B1、D1...等点的高程在计算过程中使用过2 次,拐点B4的高程使用更加多,3 次,其他的中间点B2、B3、C2、C3...的高程在计算中用过四次,这样,通过上述分析,可以得到设计高程表达式如下。

式中n 为方格总数。

用公式（3）进行土方量估算,其设计高程为64.84m,这就是此区域的填挖分界线。

2.2.3 计算方格顶点的填挖高度

根据设计高程和方格顶点的地面高程,计算每一方格顶点的挖、填高度。

将计算好的挖、填高度标注在相应方格顶点的右下方,“+”号为挖,“-”号为填。

2.2.4 计算填、挖土方量

填、挖土方量（角点土方量V角,边点土方量V边,拐点土方量V拐,中点土方量V中）分别按下式计算

式中：h- 各方格顶点的填、挖高度；P格- 方格内面积；V- 填、挖土方量。

由图2 可知,11 个挖方方格顶点,13 个填方方格顶点,通过分别列表的方式开展计算。

图2 方格网法填方模型

3 Matlab/Simulink 方格网法土方量建模研究

Matlab 是一种数学集合模块化软件,包含多种集成的数学模块,该软件提供如下建模功能,编辑器、命令窗口、调试器、简单的编程环境、完备的调试系统,程序经过模块化处理可以直接运行,并用运行自检功能,发现问题系统会自动提示问题原因。

Simulink 是Matlab 软件中的一个较大模块,它具有设计、仿真、生成代码、连续测试和验证等功能。Simulink 尤其具有以下个性功能,图形编辑、可自定义模块库、求解、动态系统建模和仿真。

3.1 数据来源

数据来源图1,实际测量中可以使用仪器获得高程数据。

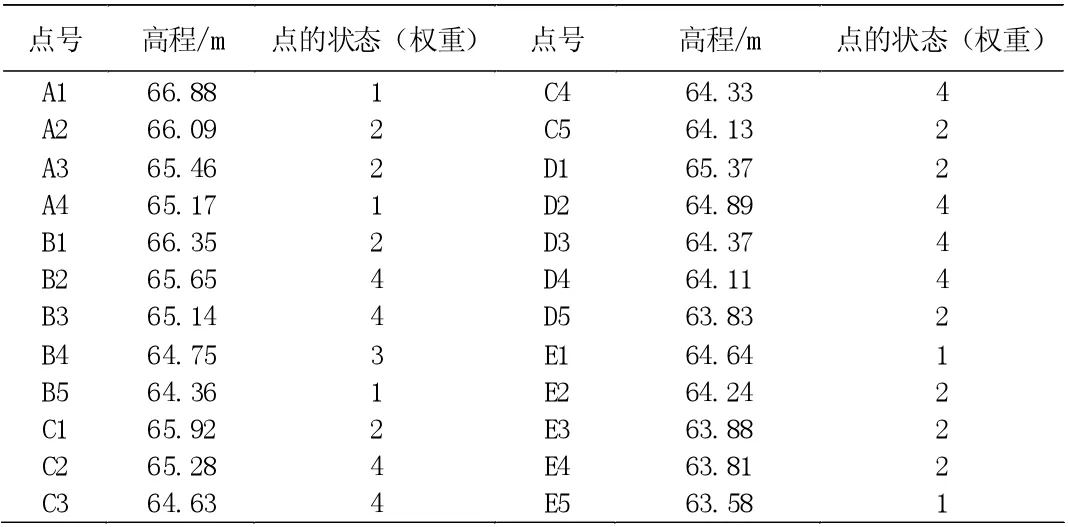
表1 方格网法原始数据

3.2 明确变量参数

明确变量参数,显然下面的量是需要考虑的：

方格网各顶点的高程,用Hi记；

方格顶点的类别（即计算方格顶点的高差所占的权重）,用Ki 记,设角点的权重为1,边点的权重为2,拐点的权重为3,中（间）点的权重为4；

设方格网总数n=15；

选用方格网的边长,设b=20m,则单个方格网的面积P格=b2=400m2；

3.3 数据处理

若H0记设计高程,则H0=（∑H角+2∑H边+3∑H拐+4∑H中）÷4×15=64.84m；

若用hi记单个方格顶点的填挖高差hi=Hi-H0；则填挖土方量Vi=hi×Ki×P格：

A1 +204 B5 -48 D3 -188 A2 +250 C1 +216 D4 -292 A3 +124 C2 +176 D5 -202 A4 +33 C3 -84 E1 -20 B1 +302 C4 -204 E2 -120 B2 +324 C5 -142 E3 -192 B3 +120 D1 +106 E4 -206 B4 -27 D2 +20 E5 -126

将表2 中的填挖方量按正负分开统计得表3。

表2 填挖土方量

表3 填挖方量（改）

此即为方格顶点的填、挖高值×方格顶点的类别（权重）×方格网的面积的四分之一的结果。对算出的填、挖方量分别进行积分,即可得到总填、挖方量的结果。并通过示波器显示出计算的过程。

3.4 建立模型

其中名为“方格顶点的填高值”的From Spreadsheet 模块选取的数据范围是表3 中E2-E14 的数据,名为“方格顶点的类别”的From Spreadsheet 模块选取的数据范围是表3中F2-F14 的数据,值为400 的Constant 模块名为“方格网的面积”与倍率为0.25 的Gain 模块相连,代表四分之一的方格网的面积。方格顶点的填高值、方格顶点的类别与四分之一的方格网面积的乘积Product 即为单个方格网顶点的填方量,而后连接Integrator 对其进行积分,得到总填方量。

最后结果在Display 模块中显示出来,并在Scope 模块中呈现出积分过程。横坐标表示总共进行了13 次积分运算,纵坐标表示每次积分的运算结果。最后的总填土方量为1851m3。

其中名为“方格顶点的挖高值”的From Spreadsheet 模块选取的数据范围是表3 中B2-B12 的数据,名为“方格顶点的类别”的From Spreadsheet 模块选取的数据范围是表3中C2-C12 的数据,值为400 的Constant 模块名为“方格网的面积”与倍率为0.25 的Gain 模块相连,代表四分之一的方格网的面积。方格顶点的挖高值、方格顶点的类别与四分之一的方格网面积的乘积Product 即为单个方格网顶点的挖方量,而后连接Integrator 对其进行积分,得到总挖方量。最后结果在Display 模块中显示出来,并在Scope 模块中呈现出积分过程。

最后结果在Display 模块中显示出来,并在Sc ope 模块中呈现出积分过程。横坐标表示总共进行了11 次积分运算,纵坐标表示每次积分的运算结果。最后的总挖土方量为1875m3。

如图2 与图3 所示,总挖方量为1875m3,总填方量为1851m3。总填方量和总挖方量在理论上应相等,但因为存在测量和计算误差,两者总有些出入。为了求得填、挖土方量相等或相近,需要多次调整设计高程,计算填、挖土方量。

图3 方格网法挖方模型

4 结论

方格网法适用于在等高线稀疏的平原地区以及较为平缓的山地进行的工程的土方量的计算。基于Matlab/Simulink应用方格网法开展土方量建模,在一定范围内能够快速、合理模拟计算出土方量计算填、挖土方量,模拟算出的填挖方量基本相等,满足填挖方平衡的要求。在直升机场开辟建设过程中能够快速、准确的模拟计算出场地的土方量填、挖量,所模拟计算数据能够对工程开展提供一定的指导。