压电材料反平面断裂问题的边界元方法研究

刘邦剑 盛冬发*

（西南林业大学土木工程学院,云南 昆明 650224）

1 概述

压电材料是指在压力作用时会在两端面间出现电压的晶体材料,这一效应被称为压电效应。而某些压电材料具有在外电场作用下压电体产生变形的能力,这被称为逆压电效应。由于这些特性的存在,可以实现机械能与电能之间的相互转换,因此压电材料被广泛运用于传感器元件当中,例如压力传感器、加速度传感器和声电传感器等[1]。然而,压电材料由于其特性在服役过程中不可避免的受到机械应力以及电应力的作用,这会使压电材料产生缺陷而过早失效。因此,对压电材料的断裂问题进行分析研究是十分重要的。

压电材料的断裂发生在多场耦合作用下,这为研究带来了困难,需要优异的数值方法来解决此类问题。边界元法作为一种在有限元法发展起来之后一种较为精确有效的方法。以定义在边界上的边界积分方程为控制方程,对边界剖分,化为代数方程组进行求解[2]。边界元法在一定程度上解决了积分奇异性所带来的困难,更是对收敛性等形式进行了数学分析,对于解决断裂问题是十分有效的。

因此,利用边界元法解决压电材料中的断裂问题是十分可靠的。本文利用边界元法,对压电材料矩形板上的反平面裂纹展开研究分析。提出满足控制方程以及边界条件的试函数,根据压电材料的基本公式推导出应力强度因子（SIFs）的结果,考虑了尺寸效应对结果的影响。与已有结果进行比对,并进行了收敛性分析,证明了结果的可靠性。

2 边界元法简介

对于边界元法所研究的边值问题,其控制方程和边界条件如下所示：

式中,R,R1和R2分别代表了域Ω,边界Γ1和Γ2的残差。

设w 为权函数,利用高斯公式,关于残差R,R1和R2的积分公式如下所示：

对于边界元法,式(7)可表示为残差形式：

式中,N为配点数目。为了获得精确解,N应该远远大于M。进一步,可将边界元法运用于压电材料的反平面断裂问题。

3 压电材料的控制方程与边界条件

对于压电材料,弹性- 压电场耦合下的反平面弹性本构方程：

对于反平面剪切断裂问题,变形与x3方向无关,即∂3/∂=0,可得用于计算的平衡方程：

采用边界元法对压电材料矩形板上的反平面断裂问题进行研究。如图1 所示,展示了压电材料矩形板边裂纹的示意图。

图1 压电材料矩形板裂纹示意图

对于矩形板上边裂纹的边界条件如下所示：

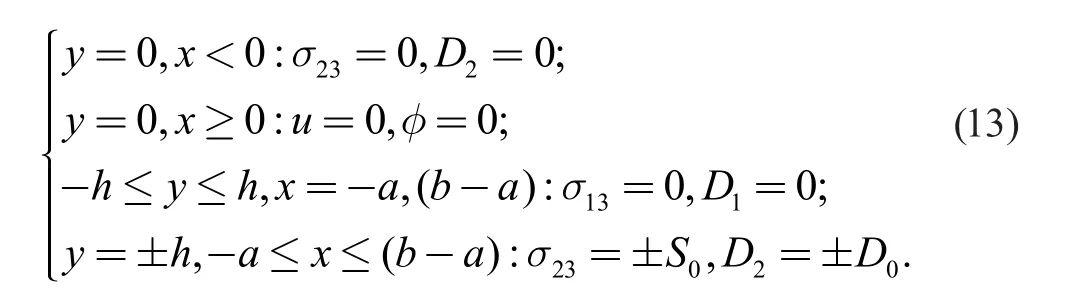
4 压电材料边裂纹算例分析

为了构建位移函数,可以采用三角级数、幂函数以及样条函数等函数作为试函数。在边裂纹以及中心裂纹的情况下,采用幂函数作为试函数。为了满足边界条件,试函数可能为位移函数的实部或虚部。

压电材料矩形板边裂纹：

对于矩形板边裂纹情况[4],位移函数为：

将式（15）代入式（11）,利用黎曼- 柯西不等式,可得应力分量：

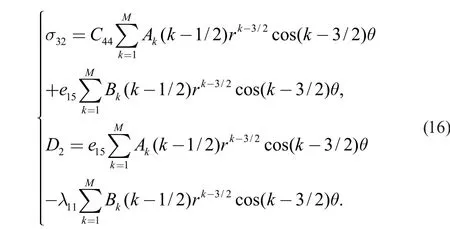
将式（16）转化为矩阵形式,可得：

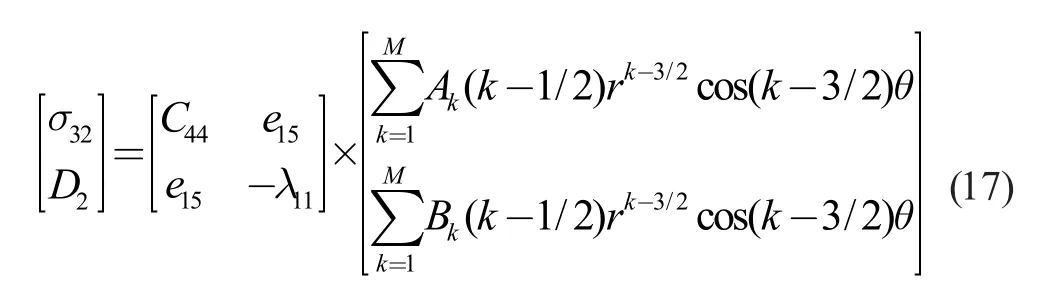
基于边界条件和断裂力学理论,III 型裂纹的应力强度因子可以表示为：

式中,Kτ和Kγ是应力强度因子和应变强度因子。Kσ和KD是弹性场应力强度因子和压电场应力强度因子。Kε和KE是弹性场应变强度因子和压电场应变强度因子。

将式(17)代入式(18)当中,可得：

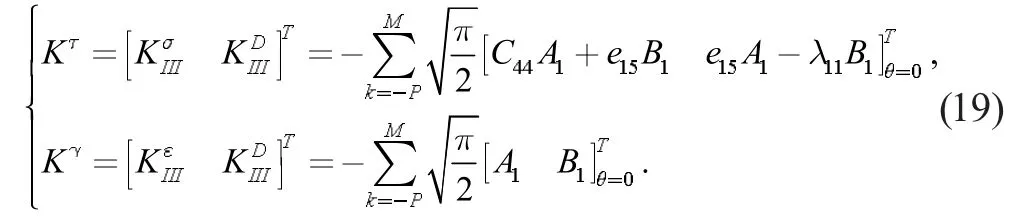
5 结果展示

据文献[5]可知,本文用于计算压电材料的参数如下所示：C44=3.53×1010N/m2,e15=17C/m2,λ11=151×10-10C/Vm。由于实验及其他客观条件的限制,通过比较压电材料与弹性解退化结果,对压电材料的反平面断裂问题进行了验证。当忽略压电效应时,材料退化为弹性材料。

如图2 所示,展示了压电材料矩形板边裂纹情况下的收敛性分析。图2(a)表示的是求和项数与不同裂纹长度下的归一化应力强度因子变化结果图。当求和项数的数目较少时,结果变化幅度较大,而当求和项数大于15 以后,结果呈现出了稳定性。图2(b)展示的是配点数对不同裂纹长度下的归一化应力强度因子影响结果图。与求和项数的规律一致,结果的收敛性说明了所采用数值方法的可靠性。

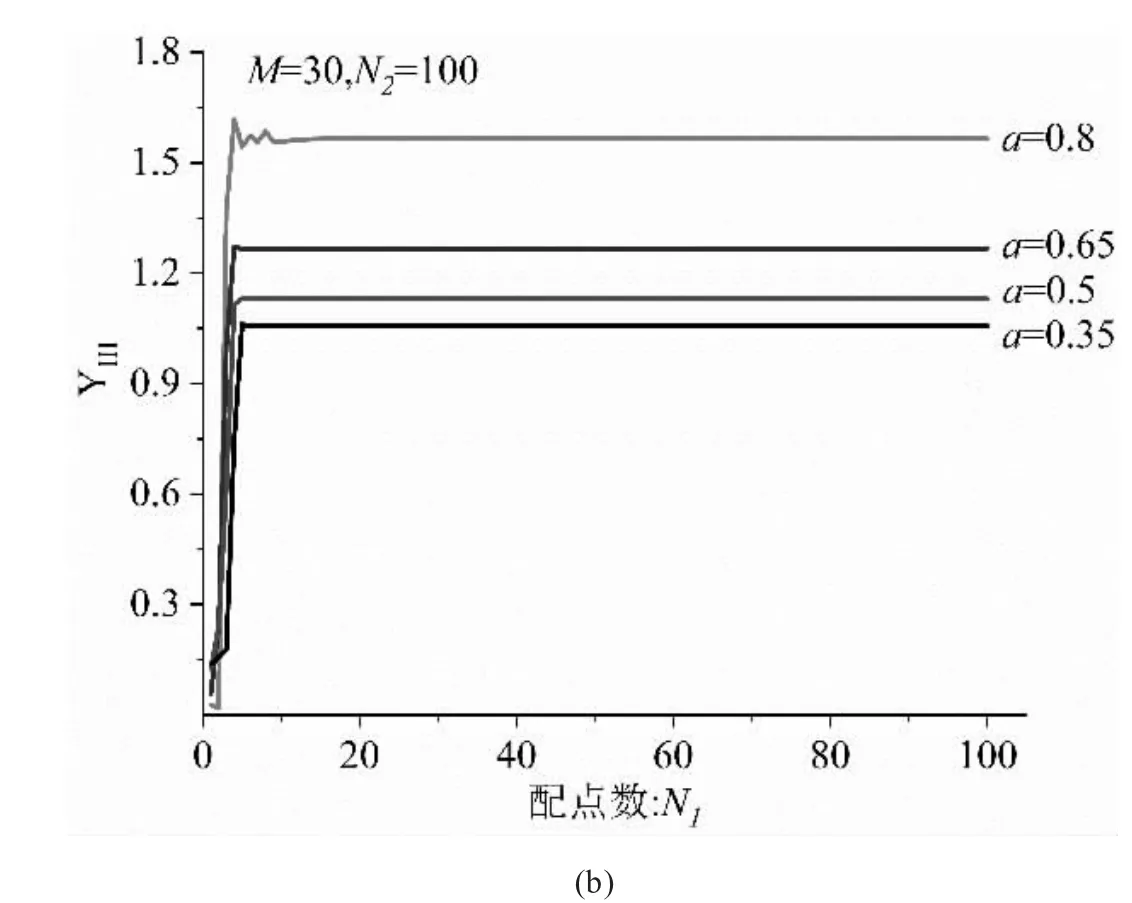
图2 边裂纹情况下的收敛性分析

如图3 所示,展示了压电材料边裂纹的应力强度因子结果图。在不同的尺寸效应下,不同裂纹所对应的应力强度因子不同。图中散点表示通过应力强度因子手册[6]计算弹性场下的结果,通过对比发现二者具有一致性,说明了边界元法对压电材料反平面断裂问题的研究是可靠有效的。

图3 归一化应力强度因子结果图

6 结论

压电材料多场耦合下会产生缺陷,有必要对其进行研究。边界元法作为一种优异的数值方法,可以减少此类问题研究的自由度。根据压电材料的本构关系推导出了反平面断裂情况下压电材料边裂纹的结果。边界法的结果具有收敛性,说明了该方法的可靠性。与应力强度因子手册结果的对比具有一致性,说明了边界元法对压电材料的断裂问题的研究结果是有效的。尺寸效应对应力强度因子有明显的抑制作用,故可以通过增加矩形板尺寸的方法来有效减少压电材料裂纹能量释放,从而抑制裂纹扩展。