接收站位形对甚低频源定位精度的影响

彭锐 顾旭东 王市委 陈欢 李光剑 罗凡 汪鑫 陆开昊 倪彬彬 赵正予

（武汉大学电子信息学院空间物理系，武汉 430072）

引 言

VLF信号是指频段为3～30 kHz的电磁波，主要源于自然界闪电[1-2]以及人工VLF台站辐射，具有波长较长、传输损耗低的特点，能在地球-电离层波导中远距离传输，因此可用于潜艇通信[3-4]和导航定位[5-6]. VLF接收机能够接收来自自然界和人工台站辐射的VLF信号，通过组网观测的方式实现VLF信号源的定位. 采用多站组网协同探测方式对VLF信号源进行无源定位时，接收站的布站位形对定位精度有着决定性影响.

在基于多站磁定向原理[7]的定位系统中，系统的定位误差与场地误差有关[8-9]. 基于多站时差原理的定位系统中，闪电探测网布站优化相关的研究[10-15]表明，定位效果会受到接收站数量、布站几何以及基线长度的影响，通过增加接收站的数量或者基线长度可得到提升. 在布站面积相同的仿真中发现，相比于菱形、三角形、平行四边形、矩形、正方形、倒三角等布站几何，星型布站下的定位误差相对较小，且误差分布呈现近似以中心位置为圆心的等值圆的规则分布，更适合闪电探测. 在针对星载探测系统和多基站雷达探测系统的定位仿真研究中，王卓群等[16]对Y型(星型)、方型及其他不规则布站构型进行了研究，发现在Y型(星型)布站定位条件下的定位误差最小，增加基线长度和卫星高度也可降低定位误差. 李世豪等[17]在对多基站雷达系统的定位仿真研究中发现，在仅增加某条基线长度的条件下，其对应基线所在方向的直线区域内的定位精度会显著提升，而其他基线方向附近区域内的定位精度并没有显著提升；且当三站位置近似处在同一条直线上时，该方向直线区域内的定位误差将大幅度提升，甚至出现无法定位的情况. 在布站优化方面，潘烨炀等[18]提出自适应遗传算法优化布局方案，与传统遗传算法相比，该算法收敛速度更快，且能够达到最优布站的效果. 代声发等[19]利用粒子群算法进行布站优化，能明显改善探测定位网内的平均误差. 窦雪倩等[20]针对不规则布站问题提出了基于几何稀释度(geometric dilution precision, GDOP)的最优布站方案，利用栅格法和遗传算法两种求解算法，其仿真结果表明，该方案能够有效提升定位系统对目标的定位能力.

上述研究主要针对百公里量级及以下的短基线辐射源定位，其目标辐射源通常位于定位网内部或者周边，探测区域范围内地球表面曲率变化带来的误差可以忽略，因此一般定位模型主要利用三维直角坐标系并忽略z轴高度变化，将探测区域近似成为平面处理. 而在长基线VLF辐射源的定位中，地球曲率的影响随着距离的增加而变大，不能忽略，相关理论研究较为缺乏. 本文基于球面模型的多站时差定位算法，利用蒙特卡洛随机试验的方法，分别仿真计算了四接收站的方型和星型两个典型构型下定位结果的均方根误差(root mean square error, RMSE)分布，并探究了布站几何、基线长度和主站选择对定位精度的影响. 研究结果对远距离VLF源定位系统的实际接收站点设置有着重要的参考价值.

1 研究方法

1.1 定位算法

与短基线定位算法不同，长基线接收站由于站间距较大，采用平面坐标进行定位会导致较大误差，故将地球本身视为规则球体，其半径取6 371.393 km，球面上任意点的坐标可用经度Long和纬度Lat表示. 由于各个接收站的距离较大，故不考虑高度因素，令台站发射机和接收机的高度均为0 m. 王涛等[21]在长基线闪电定位系统中利用类似的定位模型达到了较好的定位效果，表明该模型具有一定的准确性.

式中，Re表示地球半径.

若有N个接收站接收到某辐射源信号，则在辐射源信号到达各站之后，可以获得N−1个时差数据，记为

式中：TD为 观测得到的时差向量； Δti代表信号到达第i个副站与信号到达主站的时刻差值. 若将辐射源S位置简记为m，则可将利用模型求时间差的过程简化为下面的矩阵形式：

式中：F(m)代表正向求解时间差向量的过程[21]；TD是通过到达时间差(time difference of arrival, TDOA)定位模型推导出的到达时差向量. 寻找解辐射源位置的问题，实际就是利用观测时差向量TD来反推出辐射源位置m的问题. 利用迭代法解决该问题的过程如下：

首先，构建目标函数[21]：

式中，Cd为测量时差的协方差矩阵，假设各站测时误差相同且相互独立，可取单位阵. 目标函数代表了当前坐标值m下模型时差向量TD与实测时差向量的差异程度. 理论上，若任何测量误差为0且m为发射站真实位置，则目标函数值为0. 然而在实际计算过程中，由于误差的存在，目标函数无法取到0，只能取到极小值. 使用迭代法，从初始位置m(0)开始不断迭代计算得到m(N)，直至Φ(m)达到极小值. 使用下面的迭代公式求目标函数的极小值点的位置[21]：

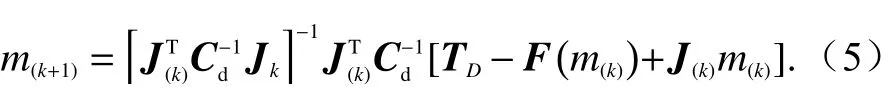
式中，J(k)是F(m)在m(k)的偏导数矩阵，

1.2 仿真方法

本文采用蒙特卡洛随机试验[22]的方法来估计实际定位误差，进而探究多接收站在给定布站构型中的实际定位效果. 实际定位误差主要源于时延测量误差，即时延测量值与真实值之间的差值，通常在μs量级[23]，例如远距离雷电脉冲在长距离传播中高频分量快速衰减，色散效应明显，脉冲波形在时域中延展导致时延测量误差. 信号在地-电离层波导中长距离传播会经过多次反射，带来额外的附加时延，产生时延误差. 考虑到时延误差的影响，在目标位置真值确定的条件下，给时差向量真值叠加随机误差，以模拟时差向量测量值，并结合上述定位算法来求解目标源的位置，得到一次随机试验的结果Pm. 通过大数量的多次随机试验可以获得大量的定位结果，然后统计所有定位结果与目标真值之间的误差，其结果可以作为该目标位置处实际定位误差的参考值.

具体流程如下：1)根据布站构型，确定各站点的经纬度信息及主站信息. 2)设置某个辐射源位置的真值P，利用上述球面模型，计算出信号从源点到达接收站的到达时间时差真值向量T. 3)为模拟实际探测中会出现的测时误差，在2)所得的时差真值矩阵中加入服从均值为0、标准差为1 μs的高斯分布的随机时间误差，得到时差测量值向量Tm. 这里主要考虑理想状态下的时延误差，相对实际时延误差可能偏小，但不影响布站构型对定位精度影响的研究.4)利用3)中所得时间测量值向量并结合上述定位算法反演目标位置，得到一次随机试验的辐射源位置的测量值Pm. 5)布站位形和辐射源位置的设定不变，重复1 000次随机试验，得到一组目标位置测量值PmM(M为重复试验次数，此处为1 000)，并计算该目标处的定位RMSE，. 其中，dis() 是 求两位置距离的函数，是第i次随机试验的目标测量值. 6)在探测区域内划分网格，计算每个格点处的RMSE，从而得到整个探测区域内的RMSE分布.

选取的探测区域经纬度覆盖范围为：经度73°E～153°E，纬度42°S～53°N，南北距离跨度约为10 564 km，东西距离跨度约为8 896 km，覆盖区域为亚洲东部及东南亚、澳洲大陆的大部分亚太地区. 为得到不同布站构型下探测区域内的定位误差分布，将上述探测区域按照经纬度划分网格，并计算格点处的RMSE，网格间距设置为1°.

在近距离定位中，其布站基线较小且主要针对接收站覆盖网内部区域目标进行定位，探测区域范围小，定位误差受布站构型影响较小，不存在定位盲区；而对于远距离定位系统，主要针对布站覆盖网外的目标进行定位，布站基线长、探测区域范围大，定位误差分布受布站构型的影响很大，尤其需要避免探测盲区的出现. 针对这种情况，本文主要探究了远距离探测中四接收站的方型和星型布站对定位误差分布的影响. 图1为方型和星型布站的构型示意图，按照逆时针顺序给出了两种构型下各个接收站的编号. 图1(a)为方型构型，其布站选点是放置在半径为r的圆内接正方形的顶点；图1(b)为星型构型，其布站选点设置在半径为r的圆内接等边三角形的顶点及中心点. 布站基线长度定义为构型外接圆的半径长度r，以此表征布站范围的大小.

图1 方型和星型布站示意图Fig. 1 Schematic diagram of the square-shaped and starshaped geometry for station configuration

2 结果分析

首先研究在方型布站和星型布站两种布站几何中不同基线长度的布站构型下，定位误差在探测区域内的分布. 图2为#3主站采用不同基线长度的方型布站下的定位误差分布，图中的白色实心点代表接收辅站，红色实心点代表接收主站. 图2(a)为基线长度为100 km的方型布站仿真结果. 整体上，从定位点到定位中心的距离角度看，距离越近，定位误差越小；距离越远，定位误差越大. 同时，误差分布具有明显的方向性，在方型边长方向上(即东西方向和南北方向)的大部分区域，定位误差随距离增加快速增加到1 500 km的量级，区域形状近似为“十字形”；而在方型的对角线方向上，定位误差随距离变化较为缓慢，大部分区域的定位误差低于700 km，区域形状近似为“花瓣形”，且主站所在对角线延长线附加区域“瓣片”的定位误差略低于另一对角线延长线附加区域. 图2(b)为基线长度为400 km的方型布站结果，其定位误差整体分布特性与图2(a)类似，出现了“十字形”区域和“花瓣形”区域，并且“花瓣形”的覆盖范围有明显向四周扩张的趋势；探测区域内所有位置的定位精度得到了大幅度的提升，“花瓣形”区域定位误差几乎全部降低到了70 km以下，较图2(a)中下降了近90%. 图2(c)为基线长度为700 km的方型布站的结果，与图2(b)的结果类似，定位误差分布同样具有方向性的分布特征，“花瓣形”区域的定位误差降低到了20 km以下，较图2(b)降低了近70%. 图2(d)为基线长度为1 000 km的方型布站结果，与图2(c)相比，整体的定位精度有了较大提升，“花瓣形”区域占了整个探测区域的大部分面积，其定位误差降低到10 km下，较图2(c)仅降低了约50%. 进一步增加布站基线长度，探测区域各点处的定位误差将会进一步降低，但每次降低的比例会逐渐下降，定位误差可能会存在一个收敛下界. 综合上述分析可以发现，在方型布站下，定位误差分布在远距离范围内具有很强的方向性，在方型边长所在直线附近区域的定位误差随距离变化很快，而在对角线方向上的定位误差随距离变化相对较慢；增加基线长度可使定位精度有明显的提升，但提升效果会随着基线长度的增加而减弱. 因此实际布站中，在了解辐射源目标位置与布站中心相对位置大致方向的情景下，可以采用方型布站，并调整布站的位置使得目标区域能够落在方型对角线所在直线区域，以达到最佳定位效果. 但对于完全没有任何位置先验信息的目标辐射源，即盲源信号，方型布站并不合适，因为当目标处于该布站条件下的“十字形”区域时，定位误差将会很大，其定位结果的参考价值不大.

图2 不同基线长度的方型布站下的RMSE分布Fig. 2 The RMSE distribution for square-shaped geometries with different baseline length

图3为采用不同基线长度的星型布站的仿真结果，主站均为#1. 图3(a)基线长度为100 km，与方型布站的结果相比，星型布站下的定位误差分布无明显的方向性，其误差等值线近似呈现以布站为中心的同心圆分布. 由于基线长度设置较小，地图中大部分区域的定位误差都在100 km以上，仅在布站覆盖范围内地区的定位误差低于100 km，远不能满足实际定位的需求. 图3(b)基线长度为400 km，定位精度有了很大的提升，大部分区域的定位误差低于100 km.在主站和辅站连线的反向延长线上的区域定位效果略优于正向延长线上的区域. 图3(c)基线长度为700 km，大部分区域的定位误差降低到了20 km以下. 图3(d)基线长度为1 000 km，大部分区域的定位误差在10 km以下. 与方型布站的结果相比，星型布站下定位误差分布没有明显的方向性，且整体定位精度都有明显提高，适合盲源定位的需求. 细节上，在主站与副站连线的方向延长线上的区域定位效果会略好一些；且增加基线长度能明显提高各区域的定位效果，但提升效果会随着基线长度的增加而减弱.

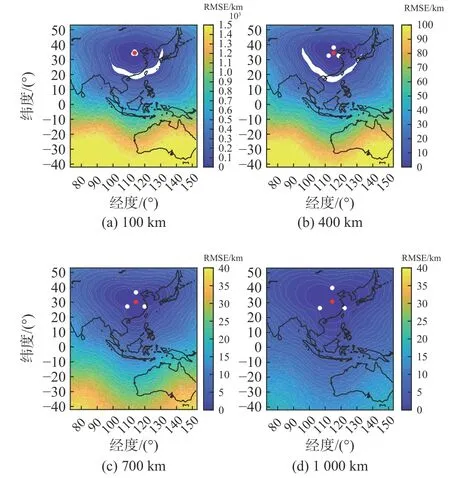
图3 不同基线长度的星型布站下的RMSE分布Fig. 3 The RMSE distribution for star-shaped geometries with different baseline length

在布站构型中，除了布站几何和基线长度外，参考主站的选取也是影响定位误差分布的重要因素.图4为不同主站的方型布站下的仿真结果. 图4(a)为#1主站，可以发现，误差分布具有明显的方向性，在方型边长所在直线附近区域的误差会随着对布站中心的远离而快速增加，而在方型对角线所在直线附近区域的误差随距离远离变化较慢，误差分布呈“花瓣形”，这种误差分布特征是方型布站下所共有的. 图4(b)为#2主站，由于其布站构型与图4(a)中的布站具有对称性，因而仿真结果也具有对称性. 通过比较可以发现，主站所在对角线直线区域的定位效果要比另一条对角线直线所在区域的定位效果好.图4(c)和图4(d)分别为#3和#4主站的结果，与图4(a)和(b)的结果类似，具有明显的“花瓣形”的定位误差分布. 由于方型布站下不同主站的选取具有相似性，因而仿真结果也具有很明显的相似性，在方型对角线方向上的区域定位误差要明显低于边长方向上的定位误差，而主站所在对角线方向上的误差要略低于另一对角线方向上的误差.

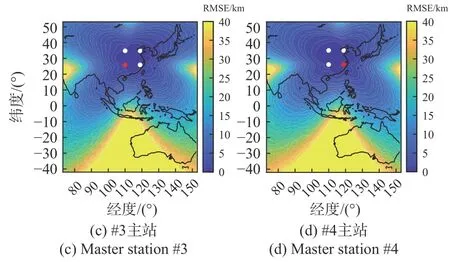
图4 不同主站的方型布站下的RMSE分布Fig. 4 The RMSE distribution for square-shaped geometries with different master stations

图5为不同主站的星型布站下的仿真结果，其中基线长度均为700 km. 图5(a)为#1主站，与图3中的结果相似，其误差分布的方向性较弱，误差等值线分布近似呈现以布站中心为同心圆，适合对盲源目标的探测. 图5(b)为#2主站，明显可以看到，由于主站设置的改变，误差分布出现了明显的方向性特征，在正三角形边长所在直线方向的附近区域内，定位误差较大，而在其他区域，如三角形的顶点与中心点的连线的所在直线方向上的区域，定位误差相对较小；另外，在顶点到中心点连线的反向延长线上的定位误差要小于正向延长线上的区域. 同时，与图5(a)中的结果相比，几乎所有位置的定位误差都有不同程度的增加，说明在星型布站中将主站设置在中心位置具有一定的优越性. 图5(c)和(d)分别为#3和#4主站的仿真结果，与图5(b)中的结果相似，具有明显的方向性特征，三角形边长方向区域的误差较大，而顶点与中心点连线方向上的误差较小，两幅图中的结果具有明显的镜像对称性，这是由布站的对称性决定的. 在星型布站的主站选择方面，将主站设置在中心站的效果要明显好于其他主站设置，整体的定位误差较低，且没有明显方向性，适合盲源目标定位；而将站点设置在三角形顶角位置时，整体的定位误差会提高，并且在三角形边长所在直线附近的区域内误差随距离的增加较快.

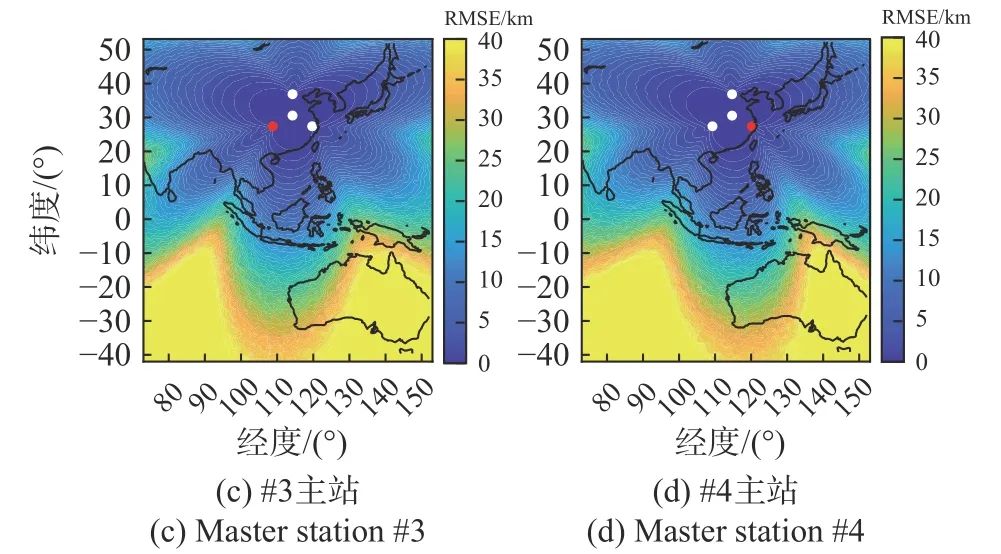
图5 不同主站的星型布站下的RMSE分布Fig. 5 The RMSE distribution for star-shaped geometries with different master stations

选择从武汉到NWC(21.82°S，114.17°E)路 径(NWC Path，南北方向)和从武汉到JJI(30.04°N，130.81°E)路径(JJI Path，东西方向)这两条典型路径，详细分析各种布站构型下的RMSE分布. 图6为随着路径上某点到布站中心的距离变化不同基线的方型和星型布站下的RMSE分布结果. 图6(a)为NWC路径上的RMSE分布. 可以看出，随着基线长度的增加，定位误差会明显降低，但降低比例会随着基线长度的增加而逐渐降低. 另外，在该路径上，基线长度为700 km的星型布站下的定位误差已经低于基线长度为1 000 km的方型布站的误差，体现了星型布站的优越性. 图6(b)为JJI路径上的RMSE分布，可以发现，在此方向上，同基线长度的星型布站的误差要略低于方型布站的误差，但是差距不大.

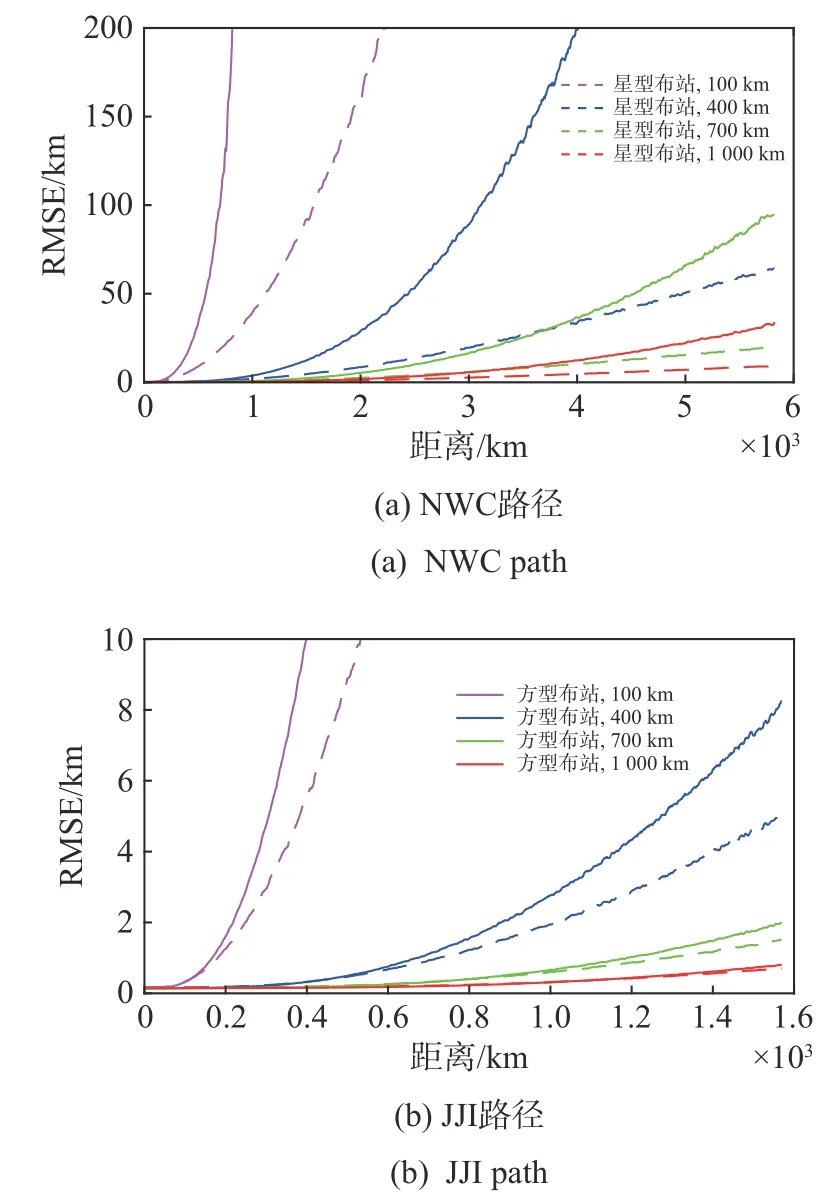
图6 不同基线长度的方型和星型布站下的RMSE路径分布Fig. 6 The RMSE path distribution for square-shaped and star-shaped geometries with different baseline length

图7为基线长度均为700 km时不同主站的方型和星型布站下的仿真结果. 图7(a)为NWC路径上的RMSE分布. 可以发现：在方型布站中，各种主站选择下的误差分布基本相同；而在星型布站中，定位误差要明显低于方型布站，且对于主站为#1和#2的定位误差要略优于主站为#3和#4的结果. 图7(b)为JJI路径上的RMSE分布，可以发现，由于距离中心站较近，整个路径上的定位误差基本都低于3 km，且星型布站整体上要优于方型布站的结果. 综上分析，在这两条路径上，基线越长，定位效果越好；星型布站的定位效果要优于方型布站；在星型布站中，主站设置在布站中心位置的效果优于其他主站设置.

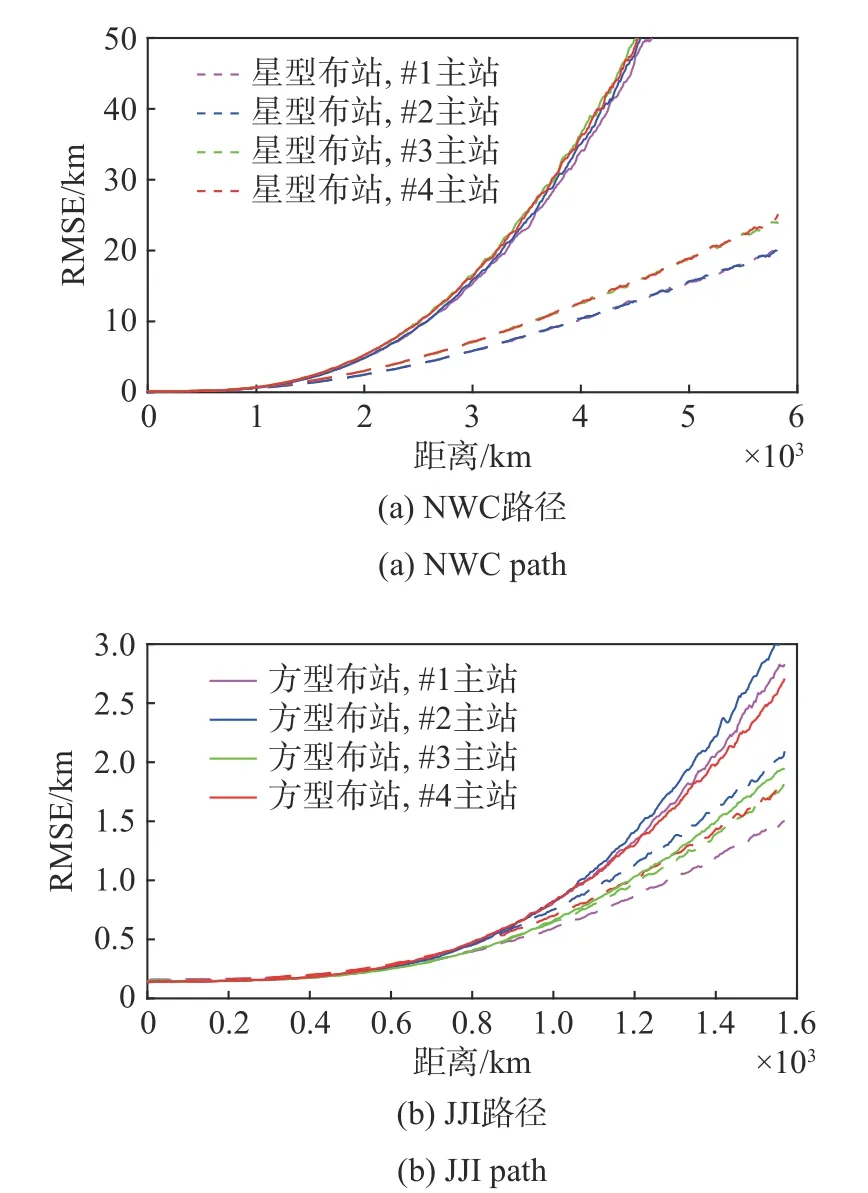
图7 不同主站的方型和星型布站下的RMSE路径分布Fig. 7 The RMSE path distribution for square-shaped and star-shaped geometries with different master stations

为方便比较不同定位构型的定位效果，表1统计了不同构型下RMSE的区域占比，即统计了在不同构型下，探测区域内RMSE处于某一误差范围的目标点数量占目标点总数的百分比. 可以看出：在同一构型下，随着基线长度的增加，定位误差低于某个误差水平的占比明显提升；当基线长度一定时，方型构型下低于某个精度水平占比基本上低于星型构型；在基线长度为700 km的方型构型中，不同主站选择下，定位精度的分布比例基本相同，各个水平下的百分比差距不到2%；而在基线长度为700 km的星型布站中，主站为#1的定位结果，要明显优于其他主站选择的结果，特别是在定位误差小于10 km这一水平上，#1主站的所占百分比为47.11%，其他主站选择条件下所占比例平均为36.51%，两者相差约10.6%.

表1 不同构型下RMSE的区域占比Tab. 1 The proportion of the area of the RMSE level for different positioning configurations

3 结 论

针对VLF多站定位中布站构型对远距离随机VLF辐射源的定位性能影响问题，本文提出了一种基于蒙特卡洛随机试验的定位误差分析方法，研究了四站条件下布站几何、基线长度、主站选取这些布站因素对定位精度分布特性的影响. 得到以下主要结论：

1)在布站几何和主站设置一定时，增加布站基线长度能够有效提升定位精度，但提升效果会随着基线的增加而减弱.

2)在方型布站中，定位误差分布具有明显的方向性，方型边长所在直线区域的定位误差较大，而方型对角线区域的定位误差较小，且定位误差分布受主站选择影响较小.

3)星型布站中定位误差明显优于同基线长度下的方型布站. 同时，星型布站下的定位误差受主站选择的影响较为明显，当主站设置在布站中心点处时的定位效果最好，且没有特别明显的方向性，而当主站设置在三角形顶点位置时，三角形边长所在直线区域的定位误差较大.

本文仅研究了四接收站下方型构型和星型构型的情况，对接收站数量和布站几何更多，以及不规则布站的情况都没有展开相关研究和讨论. 利用球面模型近似地球表面，有计算量小、精度高的优点，但对于更高精度需求的仿真实验，可以采用精度更高、计算量较大的WGS-84椭球模型来提高仿真的精度.实际中VLF信号在传播过程中会受电离层参数、地球表面地形地貌等多种因素影响，这些因素也需要在定位模型中加以考虑. 此外，仿真中使用的时延测量误差设定取值较小，适用于假定的理想情况，但是实际时延测量中误差可能更大，对定位的具体精度有较大的影响，在后续的研究中需要考虑更加真实的时延误差.