电离层吸收衰减预测方法的比较研究

王严 李雪 尹文禄 蔚娜 娄鹏

（1. 中国电波传播研究所，青岛 266107；2. 盲信号处理国家级重点实验室，成都 610041）

引 言

短波通信的高频无线电波传播模式大致可以划分为地波传播模式和天波传播模式两种. 地波传播模式下，电波传播距离很近；天波传播模式下，理论上，在特定电离层环境下，如果无线电波频率低于电离层临界频率，则发射站到近距离区域的天波传播链路均存在. 通过对电离层特性的准确获取并选择最佳工作频率，可以实现短波无盲区通信和侦察. 频率选取的准则主要包括信号能量与通信准确率，因此对近距离天波电离层吸收衰减的精确预测可以更好地为短波通信提供选频指导和场强预估.

电离层吸收衰减是天波传播过程中除自由扩散衰减外最大的衰减量，对于天波传播总衰减、场强等的计算至关重要. 远距离传播链路(收发点距离几千千米)的吸收衰减预测值一般采用国际电信联盟(International Telecommunication Union, ITU)的方法，不超过7 000 km的路径可进行射线路径分析，超过9 000 km的路径使用从拟合到测量数据的组合模型经验公式，7 000～9 000 km距离范围内则是两种方法的平滑过渡[1]. 2009年何昉等[2]提出了一种精确计算电离层吸收衰减的方法，仿真分析了吸收衰减与电波频率、仰角的关系. 2019年王红光等[3]提出了基于电磁波传播的抛物方程，计算电离层短波链路衰减的方法. 对于电离层吸收衰减的计算，大部分公开文献使用了ITU半经验模型方法，对于电子碰撞模型方法，文献中仅介绍了其中一种电子碰撞模型的仿真，且无试验数据. 因此，缺乏ITU半经验模型方法与电子碰撞模型方法预测吸收衰减的对比分析及试验验证.

本文针对近距离(大圆距离400 km以内)天波链路，利用半经验模型和电子碰撞模型计算得到电离层吸收衰减，并进行仿真与试验验证，同时对比分析了各方法的准确性. 本文工作流程如图1所示.

图1 工作流程图Fig. 1 Flowchart of the work

1 三维射线追踪方法

射线追踪技术把波场的能量近似为沿着射线传播，用光学的处理方法来简化处理波场问题，已被广泛应用于电波传播领域.

首先利用中国参考电离层(Chinese reference ionosphere, CRI)模型和质谱仪非相干散射2000(mass spectrometer incoherent scatter 2000, MSISE00)模型构建背景电离层和背景大气. CRI模型为基于可用数据源建立的电离层经验模型，对于给定的位置、时刻和日期，CRI模型可提供电离层高度范围内电子密度、电子温度、离子温度等参数的月平均值. 电离层的中性气体成分参数由MSISE00大气模型使用质谱仪、非相干散射雷达、轨道及加速度探测数据、探空火箭等获取的数据，采用最小二乘法进行数据拟合得到. MSISE00大气模型以F10.7为太阳活动影响参数，以Ap指数为地磁作用影响参数. 同时与国际参考电离层(international refrence ionosphere, IRI)模型一样，MSISE00大气模型受经纬度、季节、地方时等影响.对于给定的位置、时刻和日期，MSISE00模型提供对应时间、位置中性成分的浓度.

本文在构建的背景环境中基于三维射线追踪技术[4-5]，对近距离短波天波传播链路进行仿真分析. 三维数字射线追踪的计算过程如下：

Haselgrove首先给出了在球坐标系下的三维Hamilton方程[6]；后来，Jones将时间因子考虑进来[7]，形成了关于空间和时间的四维Hamilton射线方程；考虑到工程应用的适用性，Jones等又将四维Hamilton方程变换成以群路径P′作为积分变量的射线方程形式[8]：

式中：H为Hamilton算符；c为光速； ω =2πf为电波角频率；r、θ、 φ是射线路径上的点在球坐标系中的坐标；kr、kθ、kφ是波矢量在球坐标系中的三个分量，

v为电离层中电磁波的相速.

为求解射线方程，需求解Hamilton算符H关于频率 ω，空间坐标r、θ 、 φ， 以及波矢量kr、kθ、kφ的偏导数. Hasgrove引入的算符H与波矢量和相折射指数n关系为

射线追踪过程即为求解式(1)～(6)射线微分方程组得到特定环境(电离层电子浓度模型、碰撞模型)下在某一频率上某一地点以某一仰角和方位角出射的射线传播路径上不同点处的坐标矢量及波矢量，得到射线传播路径的主要参数，如群路径(该值除以光速即为传播时延)、大圆距离、传播模式等.

半经验模型利用射线追踪得到可用频点，而电子碰撞模型在射线追踪过程中得到可用频点及电离层吸收衰减.

2 电离层吸收衰减模型

2.1 半经验模型

电离层吸收衰减的半经验模型是根据大量的试验数据得出的. 对于天波多跳传播路径，2019版的ITU-R P.533-14报告[1]提供了点对点短波电离层反射链路吸收衰减的半经验模型，La(dB)为大圆距离7 000 km以内m个控制点的天波n跳吸收衰减，控制点是根据300 km的一个固定反射高度和90 km控制高度(每跳有两个控制点)决定的.

式(9)中：R12为太阳黑子数12个月的滑动平均值；i为反射点在110 km高度处的倾角； ATjnoon为第j控制点处当地午间且R12=0时的吸收因子，随地理纬度和月份发生变化；f(MHz)为电波频率；fLj(MHz)为第j个控制点处的fL，fL为电子回旋频率的平均值，约为100 km高度地球磁场的纵向分量，对于磁倾角I，fL=|fH·sin(I)|，fH(MHz)为110 km高度的电子回旋频率； χj为 第j控制点处太阳天顶角或102°，取较小者； χjnoon为 当 地 午 间 的 χj值 ；F(χ)=cosp(0.881χ)或0.02，取较大者，p为日吸收指数，是100 km高度处的修正磁倾角和月份的函数； φn(fv/(foE))为吸收层穿透因子，是等效垂直入射波频率fv与E层临界频率foE 之比的函数，其中fv=fcosi，详见参考文献[1].

2.2 电子碰撞模型

电离层吸收衰减是指电波通过电离层时，波的电矢量引起电子运动，电子同中性粒子及正离子发生碰撞，部分能量转移到中性分子，最终变成热能，从而引起的电波振幅的吸收衰减. 对于短波天波传播，发生在D层的吸收衰减为非偏移吸收衰减，发生在E层或F层的吸收衰减为偏移吸收衰减，因为D层内中性分子较多，碰撞衰减较大，所以非偏移吸收衰减较大；而发生在E层或F层的偏移吸收衰减很小(≤1 dB)，一般可以忽略，所以电离层吸收衰减主要指发生在D层的非偏移吸收衰减. 本文由折射指数的路径积分推导得到电子碰撞吸收衰减.

考虑磁场与碰撞条件的电波复折射指数公式为[5]：

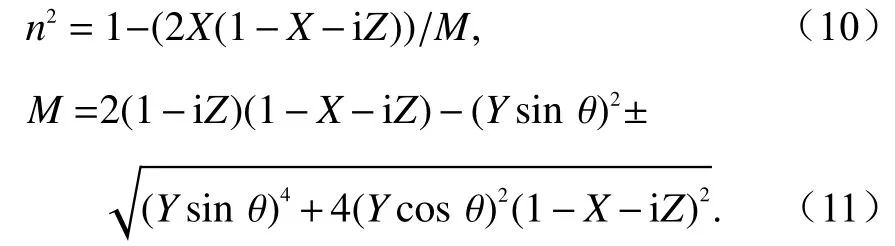
式中：θ为波矢量方向与磁场方向夹角；‘±’中‘+’、‘−’分别对应寻常波和非寻常波；X、Y、Z分别定义为

式中：fN为 电离层等离子体频率；f为入射电波频率；ne为电离层电子浓度；e为真空电子电荷；me为电子质量； ε0为真空中介电常数；B为地磁场，这里使用偶极子近似，有10−5T 为常数，Re为地球半径，取Re=6371.2km ，h为距离地面的高度，λ为地磁纬度； υe为电子的碰撞频率， υe=υen+υei， υen为电子与中性成分气体的碰撞频率， υei为电子与离子互相碰撞的碰撞频率.

以下是根据航天器发射试验数据或电离层加热试验数据或实验室模拟大气情况得到的一些 υen经验公式.

电子碰撞模型1 1973年Peter Banks提出的一种电子碰撞模型[9]：

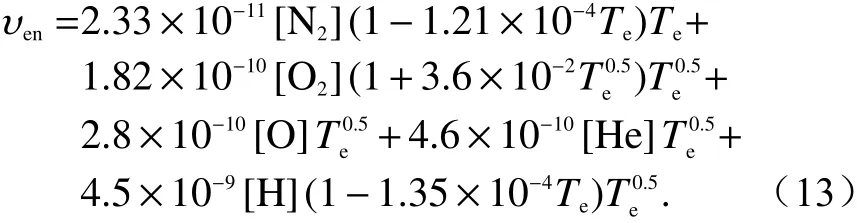
电子碰撞模型2 2003年黄文耿、古士芬提出的一种电子碰撞模型[10]：

电子碰撞模型3 2009年何昉、赵正予使用的一种电子碰撞模型[2]：

[N2]、 [O2]、 [He]、 [O]、 [H]分别代表氮气、氧气、氦气、氧原子、氢原子的浓度(/cm3)；Te是电子温度(K).

电子与离子互相碰撞的碰撞频率 υei经验公式为

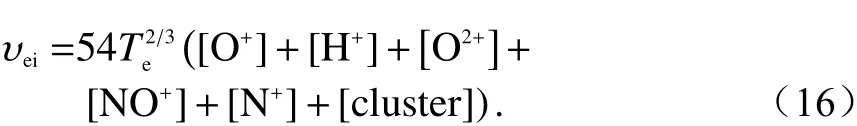
方括号中的量代表该种离子成分的浓度(/cm3).

在吸收衰减中， υen是 占第一位的因素， υei是占第二位的因素. 与υen相 比， υei很小，可以忽略.

短波信号总的电离层吸收衰减为

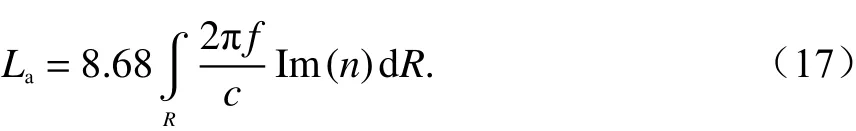
2.3 电离层吸收衰减试验计算

从发射站发射的无线电波经电离层反射后传播到接收站处的功率密度为[10]

式中：Pav为 平均发射功率；Gt为 发射天线增益；R为发射站到接收站天波传播群距离；L为环境传播引起的损耗[10]，包括电离层吸收损耗La、E层传播模式的E层吸收损耗修正Aec、Es遮蔽损耗Aq、Es反射损耗Aer、极区损耗Ah、附件损耗Az. 在半经验模型与电子碰撞模型中，Aec均包含在La中，试验时段由电离层探测情况可知无Es层，Aq=0，Aer=0；试验地区在非极区，Ah=0；根据参考文献[1]，建议Az=0. 因此在本试验中La=L−Az.

假设接收天线有效接收孔径为Ae，则接收到的信号功率为

式中，Ae=Grλ2/(4π)；Gr为 接收天线增益；λ为无线电波波长；Ls为系统损耗.

考虑外部噪声功率N为

式中，k为玻尔兹曼常数1 .38×10−23J/K；T为接收站等效噪声温度；Fa为 接收机处环境噪声因子，kT0Fa为每赫兹外噪声功率；B为信号带宽.

由此，接收信号信噪比RSN为

RSN在通信试验中根据信号Ps与噪声Pn比例计算得出，即：

测试试验中L为

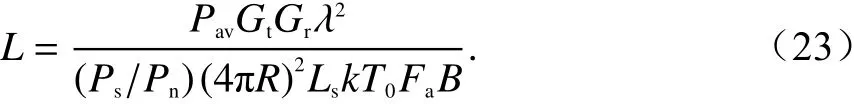
f、Pav、Gt、Gr、Ls和B根据试验实际参数获得；发射站到接收站天波传播群距离R由发射站到接收站的斜向探测图读取；根据参考文献[11]，kT0一般取−204 dB；噪声因子Fa与电波频率、地点、月份及时刻相关，在接收机处由噪声测量系统读取.

3 仿真实验

利用IRI模型和MSISE00大气模型生成一个以新乡(35.30°N，113.93°E)为圆心，半径800 km，圆心角4°，高度400 km的正南方向扇形区域的电离层环境和大气环境. 以0高度圆心为发射点进行三维射线追踪，设置射线方向是正南；电波频率为1～10 MHz，间隔为0.1 MHz；电波出射仰角为40°～90°，间隔为1°. 在生成的所有链路中，找到所有可以到达地面的链路.

选用一组典型值来三维展示射线电波频率-出射仰角-大圆距离-电离层吸收衰减的关系.

仿真试验时间为当地时间2020年9月25日10:30(R12=6，foE=2.8 MHz)，以新乡(35.30°N，113.93°E)为发射站位置，方向为正南. 根据ITU半经验模型方法得到的电离层吸收衰减分布如图2所示，根据电子碰撞模型1得到的电离层吸收衰减如图3中(a)所示，利用电子碰撞模型2、电子碰撞模型3计算得到的电离层吸收衰减与模型1的差值如图3中(b)和(c)所示.

由图2、图3可以看出，电离层吸收衰减与电波频率具有很强的相关性. 在最低可用频率附近，电离层吸收衰减存在极大值；随频率增加，电离层吸收衰减降低. 与电子模型相比，半经验模型存在电离层吸收衰减极大值的频段更宽. 图2、图3中的突起部分对应射线反射点位于E层电子浓度峰值位置，该部分半经验模型的吸收衰减计算值大于电子碰撞模型.在非极值频段，半经验模型与电子碰撞模型也存在一些差异.

图2 半经验模型吸收衰减分布Fig. 2 Semi-empirical model absorption attenuation

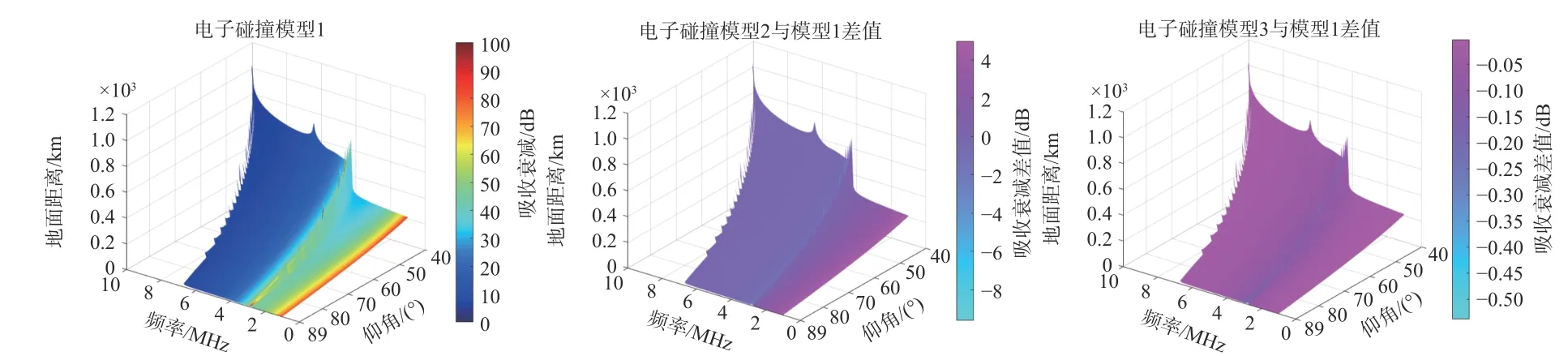
图3 电子碰撞模型吸收衰减对比Fig. 3 Comparison of electron collision model absorption attenuation

电子碰撞模型2与电子碰撞模型1的电离层吸收衰落预测值在非突起部分差值8 dB以内；电子碰撞模型1与电子碰撞模型3的预测值几乎相同，差异在0.6 dB以内. 三种电子碰撞模型所需的中性成分种类不同，但三种模型的吸收衰减预测值差异不大，在选用电子碰撞模型时，根据可获得的中性气体种类数据情况选用适合的模型.

4 试验验证

2020年9月下旬(R12=6)在北半球中纬度地区开展了多组短波电台通信试验，验证近距离天波电离层吸收衰减预测. 试验参数详见表1.

表1 试验参数Tab. 1 test parameters

其中该试验系统的天线增益根据出射仰角、电波频率由天线方向图计算. 系统损耗根据该试验系统的工程经验计算得出，误差≤1 dB. 序号1～10对应的试验时间分别为：26日15：30、27日10：30、27日17：00、25日10：30、25日15：30、26日10：30、28日15：30、29日10：30、29日15：30和29日19：00.

根据全部测试试验结果及对应时间、收发站位置的不同，预测方法得到的仿真预测值统计结果如表2所示. 仿真了各个时间点1～10 MHz，0.1 MHz步进，出射仰角40°～90°，1°步进的电波射线路径，统计的预测值最大频率(maximum frequency, MF)、最小频率(lowest frequency, LF)根据实测的最大可用频率(maximum usable frequency, MUF)、最低可用频率(lowest usable frequency, LUF)选取，选择有实测数据的部分频段，仿真值频段略宽于实测值频段. 在选取的仿真频段内，利用射线追踪可到达大圆距离D的频点个数即为仿真值的数据量. 在D处无落点但在D的前后均有落点的频率，认为该频率可到达D，根据前后落点射线计算该射线相关参数.

表2中，各个时间点电子碰撞模型的标准差均小于该时间点半经验模型的标准差，所以电子碰撞模型预测的吸收衰减值更平稳.

对表2中的实测值与各个预测方法得到的仿真值进行误差对比分析，如表3所示.

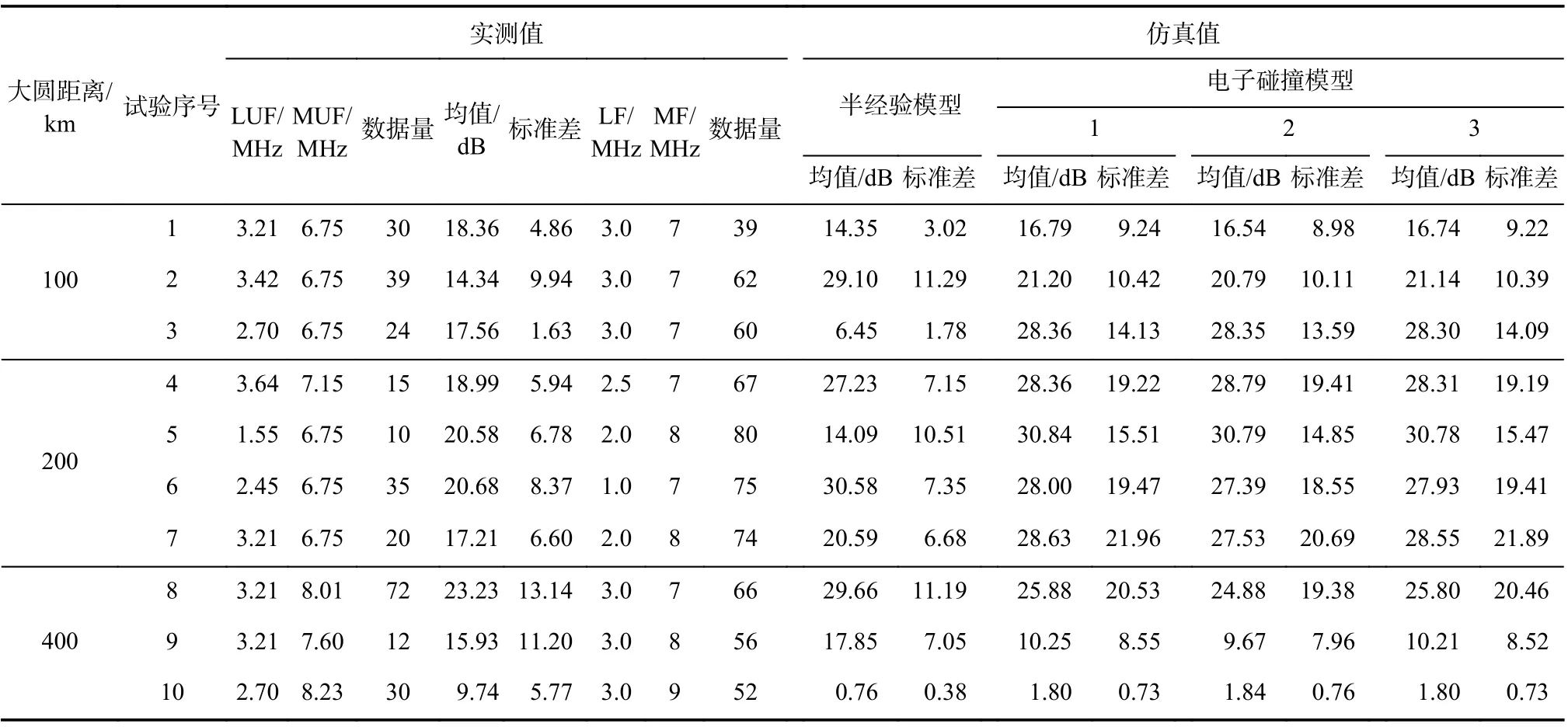
表2 吸收衰减的试验值与预测值统计对比Tab. 2 Statistical comparison of test values and predicted values of absorption attenuation

表3 吸收衰减预测值误差统计对比Tab. 3 Statistical comparison of absorption attenuation predicted value error

通过对吸收衰减预测值误差统计对比分析，发现3种电子碰撞模型预测值相近，绝对误差均值半经验模型大于电子碰撞模型，但各组数据中两类模型优劣性不一致. 因此选取其中典型的天波链路电离层吸收衰减的试验结果，与半经验模型、电子碰撞模型的预测值进行对比，结果如图4所示.

预测值与本次试验结果对比表明：

1) 预测值的LUF比试验测得的低，如图4所示.主要原因是理论上E层电子浓度是随高度增加而逐渐增加，各高度均有电波反射，但实际的E层底部电波信号回波能量非常弱. 因此在统计误差时根据实测可用频段选取仿真统计频段.

2) 图4(a)～(c)中第2、4、8组试验时间为日间，可以看出，日间半经验模型与电子碰撞模型预测值差异较小.

3) 图4(d)中第10组试验时间为日落时段，可以看出，日落时段在近距离范围内，半经验模型电离层吸收衰减值在全部可用频段都比较小，不适用于衰减预测，电子碰撞模型预测值与实测值也有一定差值，因此在该频段需要更精细的测量方法. 半经验模型值较小的原因，是日落夜间时段太阳天顶角较大，系数F(χ)取 最小值即F(χ)=0.02，La较小.

4) 在可用频段的较高频率，实测值均比较接近电子碰撞模型.

5) 如图4(a)和(b)所示，在大于E层临频的部分频段，电子碰撞模型出现极大值. 理论上这个频段部分，一个电波频率存在高、低两个仰角可到达接收站位置，其中高仰角射线的反射高度位于E层峰值处，电波信号在E层滞留时间长，电离层吸收衰减大. 但实际试验过程中，这部分高仰角信号观测到的很少，因此在半经验模型中该频段未出现吸收衰减极大值.表3中电子碰撞模型误差较大的试验组别，引起误差的部分原因就是可用频段包括该部分频段，预测值中出现了极大值.

图4 试验结果与模型预测结果对比Fig. 4 Comparison between the experimental results and the model prediction results

5 结 论

本文针对天波链路的电离层吸收衰减，利用ITU提供的半经验模型和3种电子碰撞模型进行了预测值的仿真分析与试验验证，仅从试验结果来看日间两类模型性能差异不大，而日落期利用电子碰撞模型预测得到的电离层吸收衰减优于以往采用的ITU半经验模型；在可用频段的较大频率处，实测值更接近电子碰撞模型. 仿真与试验均证实3种电子碰撞模型预测值相近，根据实际可获得大气中性成分数据.

对于吸收衰减的准确预测是短波通信与侦察总衰减预测、场强预测、信噪比预测等的必要基础和关键环节. 电子碰撞模型是基于试验场景的，若试验区域可获得的电离层环境和大气环境数据准确度提高，则电子碰撞模型预测准确度也可以提高. 而ITU半经验模型是基于大量实验数据的统计结果，对于未统计到的某些区域、某些时间可能会存在比较大的误差.