基于地质工程一体化的煤层气储层四维地应力演化模型及规律
刘英君 朱海燕 唐煊赫 孙晗森 张滨海 陈峥嵘
1. 中国石油大学(北京)油气资源与探测国家重点实验室 2. “油气藏地质及开发工程”国家重点实验室·成都理工大学
3.中海油研究总院有限责任公司
0 引言
非常规油气是指用传统技术无法获得自然工业产量、需要新技术改善储层渗透率或流体黏度等才能经济开采、连续或准连续型聚集的油气资源,例如致密油气、页岩油气、煤层气、油页岩和水合物等[1]。“地质—工程一体化”是公认的非常规油气实现效益开发的最佳途径,围绕提高单井产量这个关键问题,以三维建模为核心、以地质—储层综合研究为基础,针对在开发方案实施过程中遇到的关键性挑战,开展动态研究和应用[2-3]。
通常情况下,三维静态模型可以准确地反映地应力的当前状态[4]。但煤层气藏在长期排采过程中,孔隙压力逐渐下降,储层孔压、初次压裂裂缝、天然裂缝等形成诱导应力场,井眼周围以及储层应力场实时改变[5-6]。在重复压裂设计施工前,需要对当前地应力状态进行分析[7-8]。如果仍然采用初始地应力数据进行重复压裂设计,则容易造成重复压裂裂缝难以转向、重复压裂效果难以保证等问题[9-11]。因此,亟需开展煤层气藏长期排采过程中的地应力动态演化研究。
Biot[12]最早提出了基于弹性多孔介质的渗流—应力耦合三维地应力模型,而后Geertsma[13]为了更好地了解储层岩石的压力—体积关系,提出了孔隙—岩石体积变化理论,建立了各向同性多孔介质孔隙、岩石体积压缩性与岩石基质、岩石体积材料的弹性、黏性变形常数的关系。然而,简单的各向同性模型无法描述真实岩石的行为,由此Lekhnitskii[14]提出了各向异性弹性体理论。从20世纪90年代开始,油气藏模拟过程中考虑地应力变化得出了大量的研究成果,先后出现了大量渗流—应力耦合模型[15-16]。其中,有限元方法较其他方法,如有限差分、离散元等具有更好的适应性[17-19]。在此基础上,Hatchell等[20]、Herwanger等[21]、Onaisi等[22]将储层模拟器与地震驱动的地质力学模型耦合,建立了考虑生产或注入过程时间效应的四维动态地应力模型。然而,上述模型存在明显不足:首先是耦合计算过程中多假设理想产量,并未基于煤层气的真实排采情况,无法反映实际生产过程中煤层气藏地应力的变化;其次是未考虑储层各向异性和非均质性影响。
因此,本文首先基于地质建模成果和煤岩物性实验结果,建立目标区块三维煤层气藏数值模型,并根据区块内各生产井的排采数据进行气藏数值模拟分析,得到一定生产时间内的区块孔隙压力场变化情况。其次,建立三维有限元地质力学模型,再利用地应力实验结果和单井地应力剖面形成初始应力场,从而建立三维有限元地应力模型。最后,结合岩石力学参数各向异性实验结果,以孔隙压力变化场为不同生产时间的计算边界条件,提出了渗流—应力耦合四维动态地应力建模分析方法,并以沁水盆地某区3#煤层排水采气过程中地应力的动态变化为例。本文成果为煤层气重复压裂选井提供有益借鉴。
1 煤层气藏多物理场耦合的长期注采四维地应力模型构建
1.1 多物理场耦合理论
1.1.1 流—固耦合数学模型
由于煤岩结构的特殊性,常被处理为双孔隙介质[23-26]。本文采用双重孔隙体系,将割理视为煤岩的关键特征。煤基质为煤层气提供了储集空间,割理(面割理和端割理)与层理为煤层气和水提供了主要的流动通道。
由于煤基质被视为可压缩硬岩[27],孔隙介质的微观几何形状受到应力变化(同时岩石基质压缩)的影响,导致孔隙度和渗透率在排采过程中发生演化。为探讨应力与渗透率的关系,应用等温Langmuir方程[28],推导出煤层气排采时的本构方程[29]:

有效应力可以表示为:

式中σij表示主应力,Pa;α表示Biot系数,其值介于0~1之间;p表示孔隙压力,Pa。
煤岩应变与孔隙—裂纹应变的差异可以看作是基质在开采/注入过程中的膨胀/收缩。因此,孔隙度的变化可表示为:

式中φ表示煤岩的孔隙度,无量纲;εp表示孔隙的体积应变,无量纲;εc表示煤岩的体积应变,无量纲。
利用Betti—Maxwell互易定理描述了孔隙裂隙体积模量(Kp)与煤岩体积弹性模量(Kc)之间的关系[30]:

因此,孔隙度方程为:

式中φ0表示初始孔隙度,无量纲。
基于Reiss理论[31-33]在孔隙度小于8%的情况下,推导并简化了孔隙度与渗透率的关系为:

式中k表示煤岩的渗透率,mD;k0表示煤岩的初始渗透率,mD。
由于滑脱效应阶段尚未得到广泛认识,本研究未考虑滑脱效应阶段,归一化渗透率可表示为:
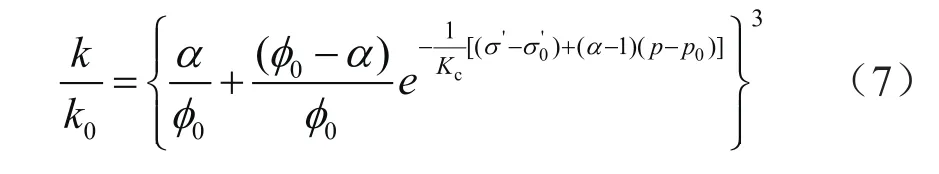
渗透率演化规律与应力、孔隙压力有关,并将其引入油气藏流动地质力学模型,实现渗透率、孔隙度与岩石物理参数的耦合。
1.1.2 控制方程与本构方程
排水采气是煤层气藏气水同时生产的一种特殊生产方式。在控制方程和本构方程中:①双重孔隙介质系统由煤基质孔隙系统和割理裂缝系统组成;②煤层气储层为气水两相流,气不溶于水;③流体运移和煤层气解吸均处于等温状态;④渗透率各向异性;⑤水的压缩性是恒定的。
1.1.2.1 气水两相的流动方程
煤层气储层流体流动方程为:

式中ρg、ρw分别表示基质中气体、液体的密度,kg/m3;k表示煤岩的渗透率张量,mD;krg、krw分别表示气相、水相的相对渗透率张量,无量纲;Bg表示气体的体积系数,无量纲;μg、μw分别表示基质中气体、液体的动力黏度,Pa·s;pg、pw分别表示基质中的气压、液压,Pa;g表示重力加速度,9.81 kg/m3;H表示埋深,m;Gg、Gw分别表示基质中气体、液体的重力,Pa;qg、qw分别表示基质中气体、液体的流速,m/s;表示孔隙度,无量纲;Sg、Sw分别表示基质中的含气饱和度、含水饱和度,无量纲。
Sg+Sw=1,根据毛细管压力曲线考虑毛细管压力,平均压力
耦合模型的外边界条件包括恒流边界和恒压边界,可表示为:

式中L表示连续外边界,内边界条件为井产量。
由于井底流动压力已知,故内部边界条件可表示为:

式中re、rw分别表示井控半径、井底半径,m;s表示气井的表皮系数,无量纲;h表示有效煤层厚度,m;pwfg、pwfw分别表示井底气体、液体的流动压力,Pa。
由于两相流体(气、水)流动与煤岩(基质和裂隙)变形相互作用,多孔连续介质可视为储层流体和煤的组合,流—固耦合作用用平衡方程来描述。煤的变形可以应用到流动控制方程中,流体流动也可以应用到煤的变形控制方程中。
1.1.2.2 应力平衡方程
地质力学模型的准应力平衡方程可表示为:

式中σ′=σ-aIp表示基于Biot理论的有效应力,Pa;τ表示剪应力,Pa;F表示体积力[35],N/m3。
煤的变形可视为线性小变形,变形方程可表示为:

同时,割理(面割理和端割理)和层理是煤层的主要结构特征,因此煤岩可视为正交各向异性材料,其弹性应力—应变关系可表示为:

式中vi表示x、y、z方向上的泊松比,无量纲;Ei表示x、y、z方向上的弹性模量,GPa。
地质力学模型的边界条件包括位移边界条件和应力边界条件。因此,混合边界条件为:

式中Tu表示位移边界,m;Tf表示应力边界,Pa。
根据式(7)的煤层气流动模型,渗透率与孔隙压力和有效应力有关,而有效应力变化依赖于地质力学模型中的孔隙压力变化。故将孔隙压力作为耦合过程中的关键参数。
1.2 基于渗流与地质力学耦合的四维应力演化模型
煤层气藏尺度较大、渗流机制复杂且具有地质力学各向异性的特点,开采过程中地应力变化的计算难度大,因此选择商业软件煤层气藏渗流模块模拟开采过程。此外,在有限差分气藏模型里完成地应力分析,工作量极大,考虑到有限元方法的优势(①适应非均质、本构模型复杂的材料;②能够直接使用弹性参数和断裂力学参数;③能够解决裂缝的交叉和分岔,而无需处理复杂的函数;④能够实现岩石基质孔隙内部及其与裂缝系统之间的流固耦合等优势),将两者结合起来,选取了基于油气藏模拟器+有限元模拟器的交叉迭代耦合方式,编制了气藏渗流有限元模拟的数据接口程序,建立了基于渗流与地质力学耦合的四维应力动态预测方法,分析流程如图1所示。

图1 四维地应力分析数值建模应用流程图
本文模型中的耦合过程可描述为:在单一时间步中,三维油气藏模型和三维有限元地质力学模型需要独立计算,然后在两个模型之间进行耦合参数互映射,完成后再进行下一时间步的计算。两个模型之间的耦合参数主要包括:由于地层岩石发生应变而变化的孔隙度、渗透率、饱和度等参数,和由于开采过程导致的压力变化。以时间ti时为例,①首先在有限差分油气藏模拟器中基于当前的孔隙度(φi)、渗透率(ki)、饱和度(Si)等参数进行渗流计算,同时,求解得到孔隙压力(pi)及的变化值(Δpi);②然后将计算得到的孔隙压力(pi)按照网格差异转换并传递到有限元地质力学模型中;③以变化的孔隙压力(pi)为边界载荷条件,在有限元地质力学模型中完成应力—应变计算,得到当前时间步应力(σi)和应变(εi)结果;④根据应力(σi)和应变(εi)结果计算下一时间步的孔隙度(φi+1)、渗透率(ki+1)、饱和度(Si+1)等孔渗参数;⑤最后将孔/渗/饱的计算结果传递回三维油气藏模型中进行下一时间步(ti+1)的计算。
1.2.1 沁水盆地东南部目标区块三维地质模型与油气藏模型的建立
目标区块位于沁水盆地东南部,区内地层构造相对简单,整体上为一西倾的单斜构造,区块内共有煤层气井22口,3#煤层分布总体趋势为东厚西薄,厚度5~8 m,埋深300~500 m,分布稳定。煤岩为半亮型煤,以亮煤为主,次为镜煤、暗煤,局部丝碳纤维结构明显。3#煤储层最大水平主应力(SH)、最小水平主应力(Sh)和垂向主应力(Sv)当量密度分别约为 1.67 ~ 2.36 g/cm3、1.11 ~ 1.58 g/cm3和2.51~2.79 g/cm3,三向应力大小关系为Sv>SH>Sh,符合正断层机制。
目标区块3#煤层及其顶板覆岩的岩石力学试验结果如表1所示。

表1 目标区块3#煤层及其顶板力学试验结果表
首先,根据测录井、地震资料,在三维地质软件中初步建立目标区块目的层地质属性模型。其次,通过室内岩石力学实验,获得煤岩岩样的杨氏模量、泊松比、压缩系数、断裂韧性等力学参数,以校正地质属性模型。第三,根据目标区块22口井水力压裂裂缝统计结果(该区块裂缝为对称缝,裂缝方位SE55°,裂缝半长为100 m,裂缝方位NW55°,裂缝半长为90 m),建立区块水力压裂裂缝模型及裂缝渗透率模型,优化目标区块地质属性模型,以获得三维静态地质模型属性参数。最后,在油气藏模拟器中导入三维地质模型的建模结果数据体,在油气藏模拟器中建立有限差分气藏渗流模型,渗流机制选择双孔双渗模型。利用排采参数完成目标区块长期排采过程气藏数值模拟计算,以获得排采过程中储层压力动态变化参数。
1.2.2 有限元地质力学模型的建立
目标区块煤储层厚度5~8 m,煤层上边界最高点与下边界最低点高差为115 m。因为储层较薄,若仅基于煤储层段构造进行建模,会因为网格畸形而导致计算不收敛。为解决此问题,在有限元软件中建立几何模型,完全覆盖煤岩层段,尺寸如图2所示的长方体为实际有限元模拟区域。在有限元软件建立的四维有限元地质力学模型中,非煤岩层段有限单元则视为顶底板灰岩与泥岩,分别赋值3#煤层构造顶面和底面的岩石力学属性。

图2 3#煤储层实际地层构造与有限元模拟区域示意图
由于模型属性参数无法由油气藏模拟器角点网格的中心点直接赋值到有限元网格的积分点上,本文利用Python开发了属性转换功能。采用球形自适应搜索算法,以赋值数据点为中心进行搜索。利用邻近点法实现地质力学参数插值,以得到三维初始地质力学模型属性参数及不同生产时间的孔隙压力,实现对有限元地质力学模型赋值属性。目标区块的煤岩各向异性如表2所示。

表2 3#煤层煤岩(井深350 m)弹性模量、泊松比各向异性统计表
由表2可知,受到割理和层理的影响,煤岩岩石力学参数表现为正交各向同性,煤岩的弹性参数矩阵可表示为:

式中G表示剪切模量,GPa。
1.2.3 地应力初始化
在完成了模型的准确描述后,对模型应力进行初始化分析,使分析从真实的应力状态开始。目标区块3#煤层初始最小水平主应力(Sh)为5.68~8.03 MPa,最大水平主应力(SH)为8.08~10.58 MPa。
1.3 模型验证
将由测井等资料得到的初始地应力现场测试地应力值与反演地应力值比较见表3,地应力实测值与反演值平均误差值小于8%。目标区块为正断层机制,且初始地应力反演结果与现场测试结果整体吻合度较高。说明该地应力建模方法及初始地应力反演结果合理、可靠,能够满足工程要求。

表3 反演与现场测试地应力值的对比表
2 长期开采过程中的四维地应力演化规律
2.1 孔隙压力变化特征
图3为模拟生产2005—2019年排采过程中3#煤储层顶面孔隙压力演化过程,长期排采过程中,孔隙压力逐渐下降。经14年的开采,孔隙压力由1.87 ~ 2.99 MPa降低到 1.10 ~ 2.20 MPa。

图3 2005—2019年煤层气排采过程中3#煤层孔隙压力变化图
以P2井为例(图4),生产前25个月,井周孔隙压力迅速由2.05 MPa下降到1.12 MPa,产气量从3 000 m3/d 上升至 10 000 m3/d。而之后 14 年,孔压减小量为0.2 MPa,截至2019年6月产气量逐渐下降至 500 m3/d。

图4 2005—2019年煤层气排采过程中P2井孔隙压力变化图
2.2 水平主应力大小(总应力)变化特征
图5、6为模拟生产2005—2019年排采过程中3#煤储层最大/最小水平主应力分布情况。长期排采过程中,每口井周围都形成了压降漏斗。截至2019年5月31日,区块最大水平主应力由8.05~10.71 MPa下降到6.51~9.57 MPa;最小水平主应力由5.99 ~ 8.20 MPa下降到 4.12 ~ 7.21 MPa。

图5 2005—2019年煤层气排采过程中3#煤层最大水平主应力变化图

图6 2005—2019年煤层气排采过程中3#煤层最小水平主应力变化图
以P20井为例,该井井周水平主应力随孔压变化趋势如图7所示,孔隙压力与水平主应力之间为正相关。受孔隙压力变化影响,生产井井周水平主应力下降。截至2019年5月31日,生产过程中井周孔压由2.65 MPa降到0.24 MPa;最小水平主应力由7.10 MPa降到 5.13 MPa;最大水平主应力由 9.27 MPa下降到 7.32 MPa。

图7 P20井水平主应力随孔隙压力变化趋势图
2.3 水平主应力方向变化特征
图8为自2005年6月至2019年6月储层最小水平主应力方向分布情况。该区域初始条件下最小水平主应力方向为NW65°,在生产过程中,区块水平主应力方向发生0°~20°偏转。相比较邻井产气量较高的井周附近,孔压变化剧烈处地应力方向偏转较明显,比如P5井,应力偏转主要受孔隙压力控制。

图8 最小水平主应力方向平面分布图
2.4 水平主应力差变化特征
P8、P11井为目标区块地质条件较好的两口邻井,目标煤层为山西组3#煤层。分别于2005年9月22日和9月18日开始生产。图9为P8、P11井裂缝有效控制区域内水平主应力差随生产时间的变化情况。排采14年,P8井井周水平主应力差由2.23 MPa增加到2.57 MPa,变化率为15.8%;P11井井周水平主应力差由2.26 MPa增加到2.37 MPa,变化率为5.02%。P11井井周水平主应力差变化率约为P8井的1/3,其产气量约为P8井的2倍。累计产气量与水平主应力差为负相关关系。

图9 水平主应力差随生产时间变化图
3 重复压裂实践
目标区块煤层厚度总体较大,区块内稳定发育的主要煤层是3#和15#煤层。前期主要开采3#煤层,投产至今已超过10年,累计产气17.8×108m3,但自2013年以来产量逐渐降低,年均递减率已由2014年的1.69%增加至2016年的9.49%,且产量继续下降趋势明显。
3.1 重复压裂井筛选
以目标区块内各井的生产动态情况为主要依据,对井资料进行分析并开展压裂井初选。首先对目标区块22口井(P1~P22井)的排采数据进行分析,排采数据覆盖范围从2005年6月27日至2019年5月31日。根据22口井在该生产时间范围内的产水产气情况,以多级排除的方式逐一对22口井进行筛选。
1)一级排除:不产气。该区块22口井处于稳定生产期,未有不产气井。
2)二级排除:产气但含水量过高。该区块22口井日均产水量在0.14~2.33 m3范围内,产水量较小。无井排除。
3)三级排除:单井产量衰竭过快。排除产气量下降的井,如P2井,截至2019年5月31日,产气量下降至500 m3/d,仅为最高产气量的1/20。
4)四级排除:排水采气难度大。排除产水量和产气量曲线走势相近,但不利于排水采气的井,如表4所示。

表4 初选四级排除井统计表
5)重复压裂备选井筛选
在排除上面4类不利于重复压裂的生产井后,根据筛选指标:产水量低于10 m3/d,产气量无明显衰减。据此,筛选出以下8口井:P6、P14、P17、P22、P21、P11、P9、P16 井。
重复压裂的目的是压开新裂缝,而压开新裂缝的一个首要前提时地应力需要产生一定程度的偏转。当目标井最大水平主应力的变化量或变化率大于等于最小主应力时,水平地应力不会产生足够的偏转,故排除P6、P14井。最终重复压裂井选定为:P17、P22、P21、P11、P9、P16 井。
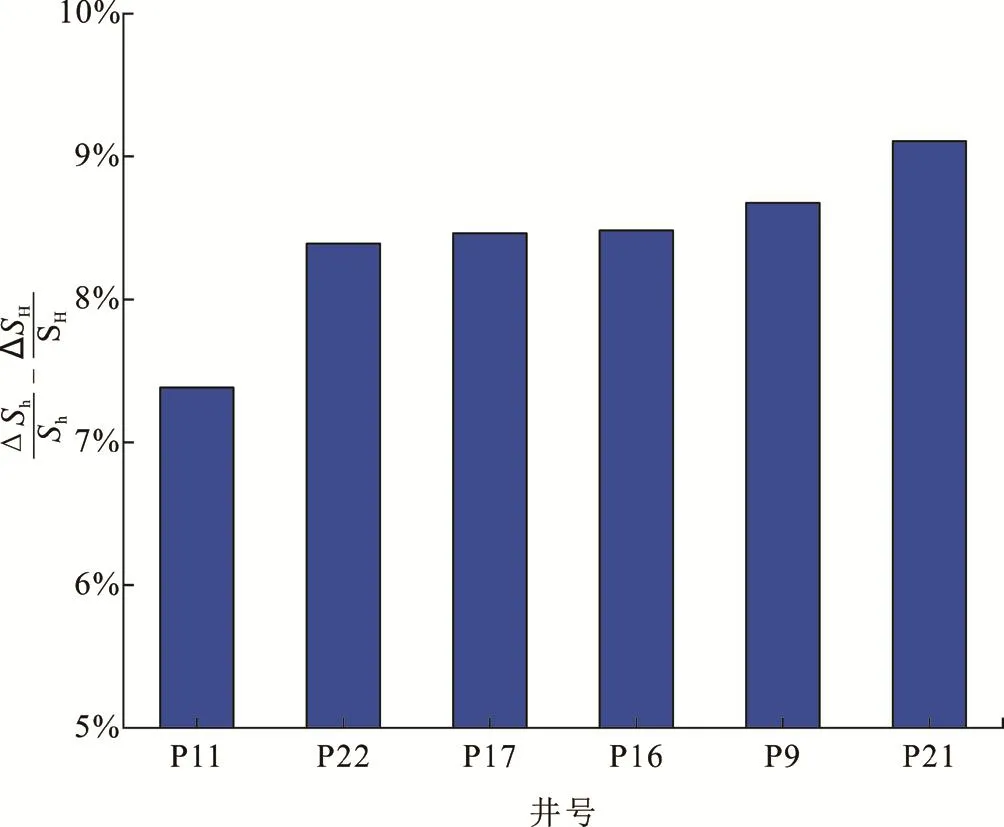
图10 目标区块6口井地应力变化结果图
3.2 重复压裂效果评价
P21井日产量一直稳定在千立方米,考虑重复压裂的经济效益等原因,因此选择P9井为基于四维地应力演化结果在目标区块所优选的可重复压裂井。2019年6月末至7月初对P9井3#煤层进行重复压裂施工(图11),P9井重复压裂后最高日产气量增加1倍,最高产气量达750 m3/d,可见,重复压裂储层改造取得了较好的效果。

图11 P9井重复压裂前后排采动态曲线图
4 结论
1)建立了煤岩储层气藏渗流与变形交叉耦合的四维地应力演化数值模拟方法,该方法所计算的目标区块初始地应力场与基于测井数据的单井地应力测量结果误差小于8%,证明了本文提出的四维地应力模型具有较高的计算准确度。
2)动态地应力分析结果表明,经14年的开采,目标区块孔隙压力下降了约0.70 MPa,最大水平主应力下降了1.14~1.54 MPa,最小水平主应力下降了1.79~1.87 MPa;产量较高的井周附近,地应力方向有明显偏转。四维地应力方法所量化的地应力可为非常规油气排采制度调整、加密井井壁稳定性分析、二次压裂优化设计等提供参考。
3)地应力偏转程度高,二次压裂时较容易产生新裂缝,建议重复压裂的P9井3#煤层压裂施工后,最高日产气量增加1倍,最高产气量达750 m3/d,现场应用取得了较好的增产效果。

