高速铁路大跨连续梁-拱现浇支架体系力学特性分析及线形控制
王广周
(中铁十五局集团有限公司,上海 200070)
在列车高速运行条件下,高速铁路桥梁结构的动力响应加剧,引起的荷载冲击、材料疲劳、结构耐久性等问题与普通铁路不同。因此,高速铁路桥梁结构必须具有足够的强度和刚度,以保证桥上轨道的高平顺状态[1]。为使高速铁路桥梁结构具有良好的动力性能,必须对桥梁结构刚度和线形进行严格控制。已有许多学者开展相关研究,黄艳军等以南广铁路大跨度支架现浇连续梁工程为例,研究砂袋加载预压的相关施工工艺[2];郭志永等以滨江大桥独塔双索面宽幅斜拉桥工程为例,探索水袋加载预压的相关施工工艺[3]。实践表明,采用砂袋、水箱等材料加载预压,不仅存在分级预压时高空堆载安全风险大、堆载物易坍塌等安全隐患,也存在预压变形测量工作量大、高空测量精度难以控制等问题。
综上所述,为了降低高空作业安全风险、减少预压变形测量工作量、提高测量精度,依托徐盐高铁跨徐沙河(100+200+100) m连续梁-拱项目,使用有限元软件对现浇支架体系进行深度数据分析,以期达到节约成本、提高效率、缩短工期的目的。
1 工程概况
新建徐州至淮安至盐城铁路是江苏省“四纵四横”高速铁路网的重要组成部分,有江苏铁路“金腰带”之称,具有京沪高铁第二通道的重要功能。徐沙河(100+200+100) m连续梁-拱是徐盐高铁关键控制性工程之一,为国内八度地震区高速铁路建成通车的最大跨度钢管混凝土连续梁-拱桥[4]。
徐盐高铁徐沙河(100+200+100) m连续梁-拱与徐沙河(河道净宽70 m)夹角为148°,0号节段采用支架现浇施工,分两次浇筑,第一次浇筑混凝土1 500 m3,第二次浇筑混凝土650 m3。连续梁共有91个梁段,全长401.8 m,主梁采用单箱双室、变高度、变截面结构,两边腹板为直腹板[5]。
0号节段顺桥向长20 m,中支点处高12.0 m,两端梁高11.06 m,顶板厚62~106 cm,腹板厚90/100~140 cm(腹板最厚处为140 cm,中腹板正常段厚100 cm,边腹板正常段厚90 cm),底板厚100.8~177.3 cm。1号节段顺桥长2.75 m,截面高10.72~11.06m,顶板厚62 cm,腹板厚70 cm~90/100 cm(中腹板最厚处为100 cm,边腹板最厚处为90 cm,正常段厚70 cm),底板厚96.6~100.8 cm。
2 现浇支架结构力学模型
2.1 支架结构设计
支架采用30根φ630 mm 、壁厚9 mm钢管,沿桥纵向为5排,间距2.25 m;横向为6排,间距分别为2.15 m、3.8 m、2.3 m、3.8 m、2.15 m。钢管之间采用φ273 mm钢管连接,钢管柱顶部放置双拼I45a工字钢作为承重横梁,承重横梁上纵向布置I25a分配梁,分配梁上铺设1.2 cm厚的钢板作为底板底模。
2.2 支架荷载与计算模型
(1)荷载取值
混凝土容重取26 kN/m3,施加在钢板上面的荷载通过混凝土容重转换[6],分布情况见表1。

表1 荷载分布 kN/m3
内模及支撑体系重取0.9 kN/m2,外模及支撑架每侧自重取8.0 kN/m2,方木容重取8 kN/m3,钢板底模容重取78.5 kN/m3,钢材容重取78.5 kN/m3,施工人员及施工设备荷载取2.5 kN/m2,倾倒、振捣产生的荷载取2.0 kN/m2。
(2)荷载组合
强度组合:永久荷载×1.2+可变荷载×1.4;刚度组合:永久荷载×1.0+可变荷载×1.0。
(3)计算建模
采用有限元软件midas建立三维空间模型,0号-1号现浇段支架模型见图1。
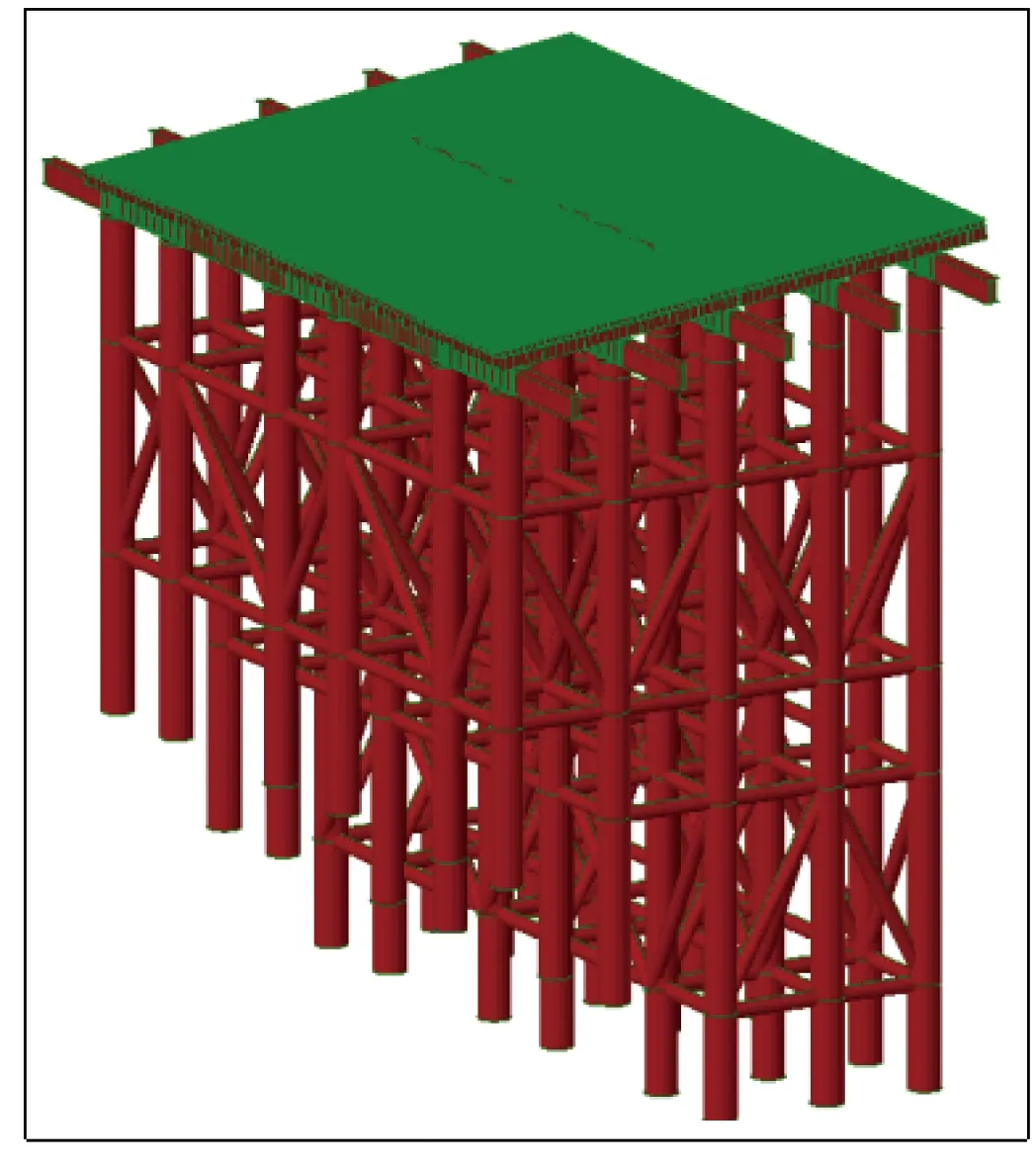
图1 0号-1号现浇段支架模型
①单元类型
混凝土用实体单元模拟,模板用板单元模拟,其他构件均用梁单元模拟。结构受到的荷载主要是钢管立柱、承重横梁、分配梁、内外模板及支撑架、底模板、施工荷载及混凝土自重。
②建模边界条件
钢管底部支承平动Dx、Dy、Dz方向全部约束,转动Rx、Ry、Rz方向非约束;钢管排架及排架之间采用刚性连接,钢管顶部承重横梁与排架采用刚性连接,承重横梁与分配梁之间采用刚性连接,分配梁与底模板之间采用弹性连接[7]。
3 底模板力学性能分析
3.1 底模板计算
底模板为12 mm厚钢板,有限元计算结果见图2。

图2 底模板的力学性能分析
钢板局部综合应力 99.4 MPa<[σ]=215 MPa,强度满足要求;钢板最大挠度1.1 mm<[f]=L/400=5.38 mm,刚度满足要求。
3.2 底模分配梁计算
底模分配梁计算结果见图3。

图3 底模板分配梁的力学性能分析
计算结果显示:底模分配梁 I25a 工字钢最大正应力 81.6 MPa<[σ]=215 MPa,最大剪应力32.7 MPa<[τ]=125 MPa, 强度满足要求;底模分配梁 I25a 工字钢最大挠度 0.77 mm<[f]=L/400=5.375 mm,刚度满足要求。
4 钢管支架力学性能分析
4.1 承重梁计算
承重梁采用双拼I45a型钢,计算结果见图4。

图4 钢管支架承重梁双拼的力学性能分析
由图4可知,双拼I45a型钢的最大正应力51.0 MPa<[σ]=215 MPa,最大剪应力44.0 MPa<[τ]=125 MPa, 强度满足要求。双拼I45a型钢最大挠度0.95 mm<[f]=L/400=5.38 mm,刚度满足要求。
4.2 钢管支架强度计算
钢管支架立柱规格尺寸为φ630 mm×9 mm,立柱间采用φ273 mm×5.3 mm 钢管连接成一个整体,计算结果见图5。
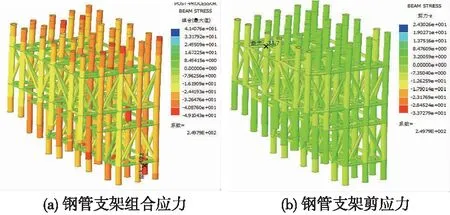
图5 钢管支架的强度计算
计算结果显示,钢管支架最大正应力 49.1 MPa<[σ]=215 MPa,最大剪应力33.7 MPa<[τ]=125 MPa,强度满足要求。
4.3 钢管立柱稳定性计算
钢管立柱稳定性计算结果见图6。
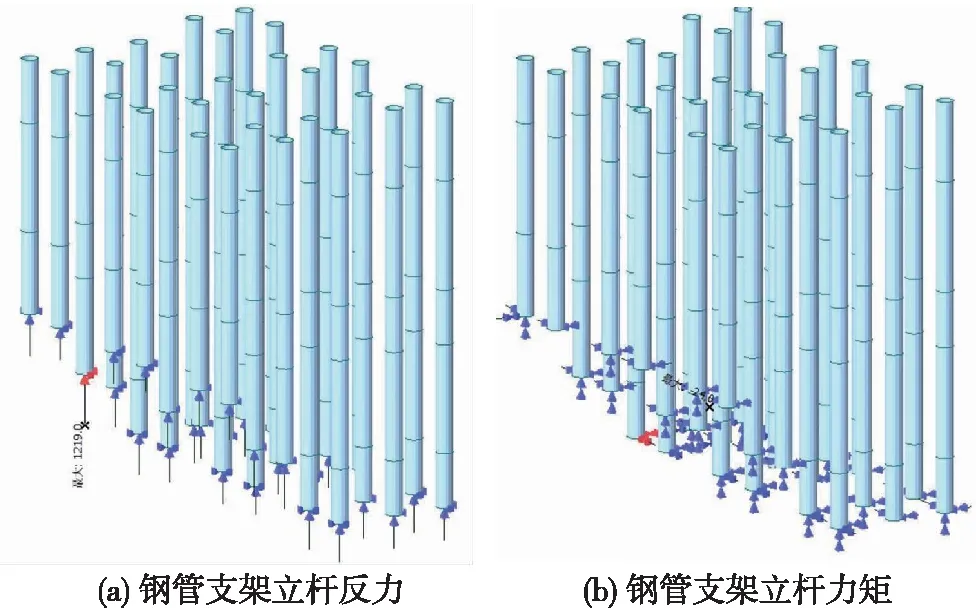
图6 钢管立柱稳定性计算分析
按最大荷载考虑钢管立柱的稳定性,取最大轴力为N=1 219.0 kN,最大弯矩为M=24.0 kN·m。
根据GB50017—2017《钢结构设计规范》,构件长细比计算公式为
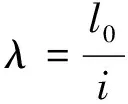
(1)
式中,μ为压杆的计算长度系数,一端铰接,另一端固定,取 0.7;i为构件截面对主轴的回转半径,取 210.8 mm;l0为压杆计算长度,取3 850 mm。经计算,构件长细比为18.3。
钢管正应力为
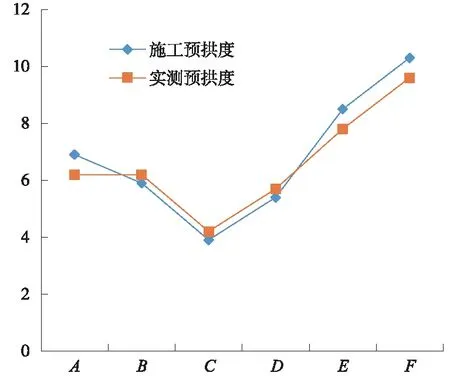
95.4 MPa (2) 式中,构件稳定系数φ=0.984;γ为塑性发展系数,取1.15;W为毛截面抵抗矩;β为等效弯矩系数,取1.0[8]。经计算,正应力满足规范要求。 由于墩身属于非变形部分,整个支架系统拼装完成后,只需要对能产生变形的支架部分进行预压。施工方法:承台施工时,预埋带固定锚头的钢绞线,支架搭设完成后,顺桥向布置8排I25工字钢张拉平台,利用张拉平台张拉钢铰线,形成的张拉力反作用于支架,达到对支架预压的目的[9]。 消除支架的非弹性变形,获得支架的弹性变形,验证支架的承载能力;根据测得的数据推算0号-1号节段底模的预留变形值,确保支架的使用安全及梁底线形,另外,还可验证支架搭建是否合理,强度、刚度及稳定性是否满足要求[10]。 预压荷载按承受荷载(去掉墩顶部分梁体钢筋混凝土重量+施工荷载)的1.1倍计算[10]:①0号-1号节段作用在支架上的钢筋混凝土重量为45 529 kN;②模板组合总重量为1 932 kN;③施工人员、机械堆放荷载按15 kN计算,则 预压荷载=(①+②+③)×1.1=52 220 kN (3) 在承台范围内预埋反支点预压钢绞线,以承担预压荷载(钢绞线预埋深度为1.4 m,并加4层φ16防崩钢筋网片,钢绞线末端设锚固钢板并压花),反支点预压钢绞线共布置20束(单侧),顺桥向布置(见图7)。钢绞线单束7根,每根由7φ6 mm钢丝捻成,单根抗拉强度标准值fpk=1 860 MPa,弹性模量Ep=195 GPa。 图7 张拉平台平面布置(单位:mm) 钢绞线抗拔力验算应满足:①现场钢绞线反拉实际最大拉力<②钢绞线自身极限抗拉值<③钢绞线锚固入承台混凝土极限抗拉值。 (1)现场钢绞线反拉实际最大拉力 采用1 305 kN的张拉力即能满足预压要求,为保证0号-1号节段支架稳定,实际张拉控制力为1 430 kN。 (2)钢绞线自身极限抗拉值 根据GB/T5224—2014《预应力混凝土钢绞线》,钢绞线公称横截面积Ap=191 mm2;根据TB10092—2017《铁路桥涵混凝土结构设计规范》,锚下控制应力σcom≥0.75fpk,则单束钢绞线极限抗拉值为1 865 kN。 (3)钢绞线锚固入承台混凝土极限抗拉值 根据GB20010—2002《混凝土结构设计规范》,ft=1.71 N/mm2,βh=0.95,βs=2,αs=20,ho=1.3 m,um=2 m,σpc,m=0,η1=1,η2=3.75>η1,η=1,(0.7βhft+0.25σpc,m)ηumho=2 956 kN。 综上,有①1 430 kN<②1 865 kN<③2 956 kN,即实际反拉作业时,钢绞线不会崩坏,承台混凝土不会开裂。 该连续梁0号-1号节段支架预压采用钢绞线反拉的方法进行,压重顺序应按紧挨墩身一排向两侧对称进行,根据箱梁截面的变化特点及混凝土浇筑顺序对应压重,预压按承受重量的60%、100%、110%三级加载(卸载时相反)。 在搭好的支架预压平台上布设监测点,并做好标记,变形监测点布设情况见图8。 图8 监测点平面布置 支架加载前,监测并记录各监测点初始高程,初始沉降量H1设定为0;每级加载完成1 h后,进行支架的沉降监测,并以6 h的间隔循环监测,满足相邻两次沉降平均值之差不大于2 mm时,方可进行后续加载;加载至承受重量1.1倍时,以6 h的间隔循环监测,当连续12 h监测沉降平均值之差不大于2 mm时,方可进行卸载,沉降值定为H2;分级进行支架卸载,每卸载一级进行一次支架监测,支架卸载完成6 h后,进行末次监测,沉降值定为H3[11]。通过以上方法,可以检验加、卸载过程中变形观测和计算的准确性,对误差数据进行修正[12],监测沉降结果见表2。 表2 521号墩支架加载各阶段沉降量计算 mm 根据监测数据结果,通过对比该断面其他点位变形量,可以找出差异点,并剔除异常数据,其余点位变形量的平均值即为该断面的总变形量,以此类推计算所有断面的总变形量[13]。依据该方法,计算确定所有断面的总沉降量、非弹性变形值及弹性变形值[14],其计算结果见表3。 表3 所有断面变形量计算 mm 该桥施工预拱度=设计预拱度(设计图给出)+弹性变形值,根据施工预拱度调整立模高程[15]。所有断面施工预拱度见表4。 表4 所有断面支架预拱度计算 mm 通过模拟分析,求得主梁上各断面的变形值,等待成桥后,监测各断面的梁体高程,求得主梁上各断面的实测预拱度值(见表5),最终得出主梁的施工预拱度与实测值对比曲线[16](见图9)。由图9可知,混凝土浇筑完成后,梁体线形基本与设计吻合。 表5 主梁的施工预拱度与实测值对比 图9 主梁的施工预拱度与实测值对比(单位:mm) 以徐盐高铁跨徐沙河(100+200+100) m连续梁-拱0号-1号梁段为工程背景,运用有限元进行模拟分析,验证现浇支架施工的准确性和可行性。经过反支点预压加载,消除支架非弹性变形,并通过监测得到支架的弹性变形值,从而确定施工合理的预拱度数值,为立模高程提供可靠的依据。研究表明,在高铁大跨大体积连续梁-拱桥现浇支架体系中,采用钢绞线反支点预压替代传统压重预压工艺,可解决传统压重预压堆载耗时长、安全风险高等问题,并大幅降低制作预压材料及机械租赁成本。为今后大跨大体积现浇支架体系预压提供参考。5 支架预压
5.1 预压目的
5.2 预压荷载
5.3 反力点布置及钢绞线抗拔力验算
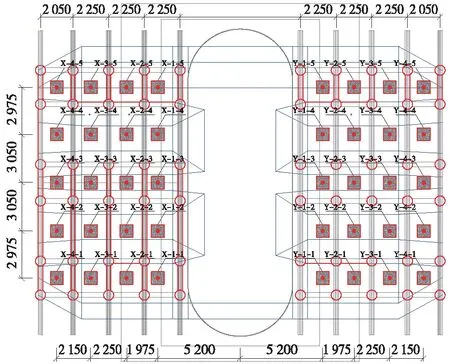
5.4 预压方法
5.5 监测点布置
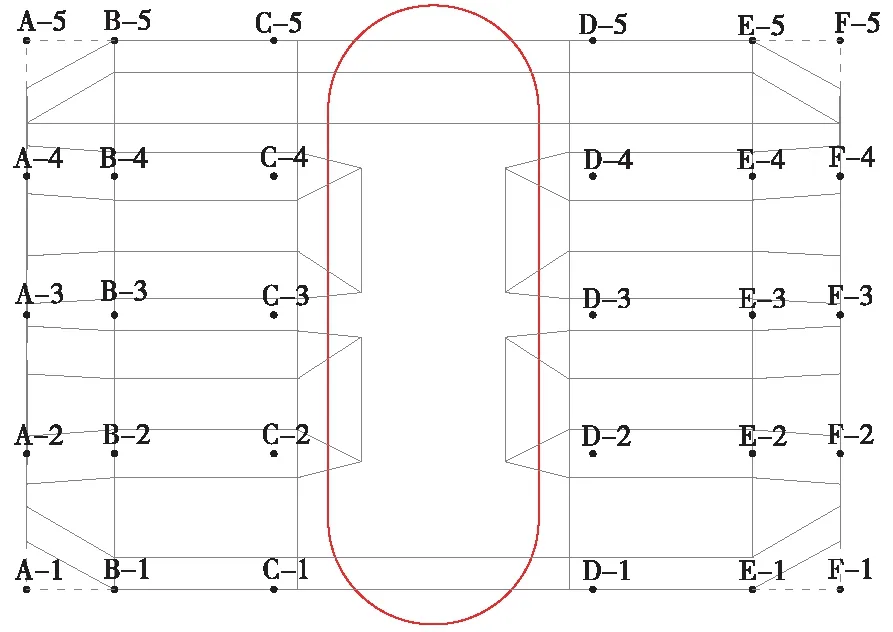
5.6 监测方法

6 支架预拱度设置及梁体线形分析
6.1 反支点预压数据分析
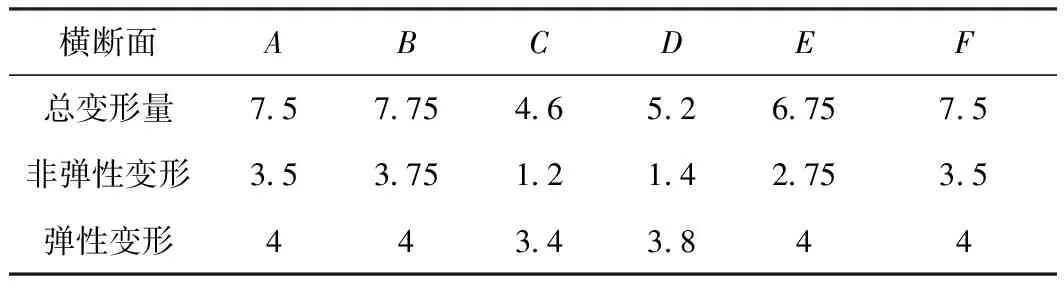
6.2 施工预拱度调整

6.3 主梁线形分析
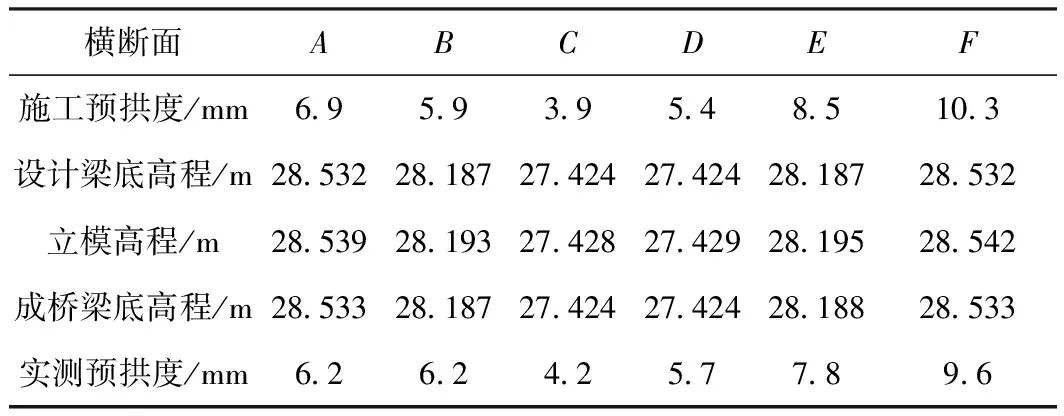
7 结论

