基于多因素耦合改进的LSTM道路交通流量预测方法及应用

吴恩泽、熊建辉、宋程

（广州市交通规划研究院有限公司,广东广州510000)

0 引言

道路交通流量是指在指定时间段内，通过道路某一地点、某一断面或某一车道的交通实体数[1]，道路交通流量预测主要是对车流总量、车型结构、时间分布等参数进行预测。道路交通流量预测因交通流的随机性、非线性、空间依赖性、时间周期性、构成复杂性往往精准度不高。为提高预测准确度，研究者提出了多种复杂的、高精度的预测方法和模型，基本可分成三类：第一类是早期基于统计理论为基础的预测，包括时间序列方法、卡尔曼滤波、贝叶斯方法和马尔可夫链模型等，此类预测方法较为简单，但受数据序列本身影响较大，且无法适应多种外部因素影响的交通流特性。第二类是基于机器学习的方法，包括K 邻近算法、支持向量机法、卷积神经网络等，普遍特点是无需精确的数学或者物理模型，通过自学习参数调整来对交通流的变化进行预测，具有良好的鲁棒性、精准度。第三类是将多种不同类型的前两类方法组合进行预测，通过组合的方法弱化单一模型自身缺陷。以上方法一定程度上会考虑道路交通流量部分外部影响因素，但较少能够全面将多种不同类型的外部因素耦合分析并融入模型，为此，本文展开相关研究。

1 改进的LSTM 模型

1.1 长短期记忆神经网络

长短期记忆神经网络（LSTM）是Hochreiter 和Schmidhuber 基于循环神经网络（RNN）提出的变体，其结构由一个输入层、数个隐藏层和一个输出层组成，模型网络的关键在于记忆单元能够克服原始的RNN 因训练时间、网络层数增加而易出现梯度爆炸或梯度消失的问题。

LSTM 记忆单元输入门、遗忘门、输出门分别：

输入变化及状态更新方式：

式（1）～式（6）中:Wu为权重矩阵；b为偏移量；σ为sigmoid激活函数；*为向量外积计算。

1.2 多因素耦合改进的LSTM

实际道路交通流量变化往往还与多类外部因素相关。第一类是空间特征影响，如周边路网影响，特别是上下游、平行道路情况，如周边道路施工、范围内重大事件、交通管理政策、上下游衔接道路交通能力容量限制等，这些空间变化特征对于预测主体道路交通流量的影响是显而易见的。第二类是时间特征影响，道路交通流量往往具备周期性变化趋势，其分布特征为固定周期循环往复等。此外，还有一部分外部特征对于城市交通状态的影响也是不可忽视的，例如天气与道路交通流量也息息相关，一般情况下恶劣天气状况可以显著改变交通流的实时分布，充分考虑外部因素的影响可以提高交通流量预测的准确度。一些突发事件特别是类似于新冠肺炎疫情的影响、重大公共安全卫生事件与社会经济相互影响明显，在中期、长期交通流量预测中的影响不可忽视。考虑以上多种因素耦合对道路交通流量的影响，本文提出了改进的Mult-LSTM 模型，模型框架如图1所示。

图1 耦合多因素的改进LSTM 模型框架

2 实例分析

2.1 数据来源

此次研究选取广州市广和大桥为研究对象，历史交通流量数据来自广和大桥收费站系统，数据周期为2017年3月至2021年3月，数据颗粒度为日，共包含客车、货车的11 种车辆类型。数据格式如表1所示。

表1 车流数据格式

外部影响因素数据中的天气数据来自气象接口数据记录（中国气象网），其中气候因素包括天气（雨、雪、晴、阴天等天气）因素，日期因素包括当天是否为重大节日（如春节、五一等）以及当天是星期几。其他上下游道路施工及交通管制信息主要来自互联网信息数据，将多种因素进行耦合分析[2]。

2.2 数据处理及数据集划分

数据预处理主要有四大步骤。

2.2.1 数据清洗

对历史交通流量数据集内数据进行数据清洗，清理异常值及补充缺失值。

2.2.2 外部因素特征提取

对外部特征天气、周边道路施工、交通管理措施等采用独热编码标记并特征提取。时间特征按工作日、非工作日、节假日等属性进行加权处理。

2.2.3 归一化处理

交通流量数据随时间变化的幅度较大，为了消除数据大小差异给预测精度带来的影响，一般用归一化的方法对数据进行变换。

2.2.4 数据集划分

80%的数据作为训练集，其他的数据作为测试集。

2.3 模型参数选择

在进行模型训练时，需要进行网络参数调整，涉及参数包含两类：一类是模型本身学习迭代自动优化的参数，不需要人为设定；另一类是人工设置参数，这部分参数也被称为超参数，需要在模型训练前就确定好，通常先进行经验赋值。

本文确定了一个LSTM 层的网络结构，在确定网络基本结构后再设定其他超参数。输入层、输出层、迭代次数、学习率分别设定如表2所示。

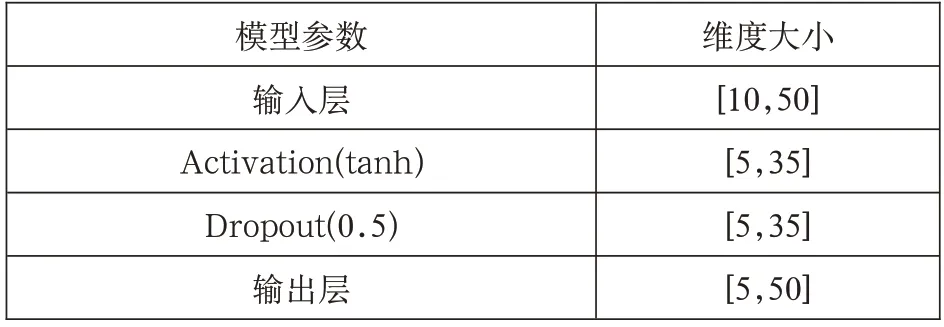
表2 LSTM 模型参数取值范围

2.4 结果分析

为了评价预测结果的性能，本文分别以均方误差（Mean Squared Error，MSE）、均方根误差（Root Mean Squared Error，RMSE）、平均绝对误差（Mean Absolute Error，MAE）作为指标判断模型方法的精准度。此次模型针对广和大桥4 种类型车流的预测结果及实际值的比较如图2所示。从图中可看出，改进的LSTM 模型能正确反映交通流变化的大体趋势，在交通流处于平峰时与真实情况吻合得较好，但在流量数据处于极端值时，模型预测值与真实值有一定差异[3]。

图2 二、三、四、五类车预测结果

通过均方误差、均方根误差、平均绝对误差三个指标来看（见表3），此次改进模型对三、四、五类车流预测效果可观，对于二类车流预测误差相对而言最大。

表3 LSTM 模型评价指标情况

表3 （续）

3 结论

一是考虑道路交通流量的时空复杂特性，提出了改进的Mult-LSTM 的交通流量预测模型、方法，应用广州市广和大桥历史收费实际流水数据测试结果表明，Mult-LSTM 在中期交通流量预测方面表现出了不错的适应能力，与ARIMA、LSTM 在同一个数据集上进行的对比实验表明，改进后的模型取得了更好的预测效果，此次提出的模型在交通流量预测应用的有效性即平均预测的精度较原始的LSTM 方法提高了7.5%左右，与ARIMA 及LSTM 模型对比，本文提出的模型是一种性能更好的交通流量预测方法。

二是改进的LSTM 模型预测精度虽然有所提高，但准确率还有一定提升空间，后续可从更加多维的角度加强外部特征对预测精准度的影响，这也是该模型下一步的优化方向及目标。