川滇地区地震动预测模型及其对2021年漾濞6.4级地震的适用性

王中伟，胡进军，张 辉，靳超越，胡 磊

（中国地震局工程力学研究所，中国地震局地震工程与工程振动重点实验室，黑龙江 哈尔滨 150080）

引言

地震动预测模型、地震动衰减关系、地震动预测方程或地震动模型是工程场地地震安全性评估、地震动参数确定和地震区划的重要基础。研究表明，由于地震构造区存在差异，不同地区的地震动的衰减特征可能存在显著差异［1-2］，因此区域地震动预测模型通常是基于该地区的强震记录回归分析得到，例如美国在2008 年建立的NGA（next generation attenuation，NGA）地震动衰减关系以及2014 年发布的NGA-West2 模型。受各种条件限制，我国在汶川地震之前的强震动记录相对较少，因此我国的很多衰减关系［1，3］是基于地震烈度资料转化得到的，然而李小军等［4］研究后发现对于中小震近场地震动参数的估计不宜采用此类地震动衰减关系。随着国内强震动观测网络的建设与完善，我国西部地区近年来已积累了丰富的强震记录，与王玉石等［5］提出的川滇地区地震动衰减关系所选择的地震动数据相比，现有的地震动数据不论是数量还是质量都相对更高，因此有必要基于现有的川滇地区地震动数据，建立更符合该区域特征的地震动预测模型。

为了建立川滇地区新的地震动预测模型，文中选取了近年来川滇地区的大量地震动数据，采用随机效应回归模型［6］建立了适用于该地区的地震动预测模型，并分析了模型的事件间残差和事件内残差的分布，再通过与该地区已有的地震动预测模型对比分析，最终验证了文中预测模型的合理性。为了探究文中预测模型对川滇地区地震的适用性，文中选取了最近在该地区发生的漾濞地震作为研究对象。北京时间2021年5月21日21 时48 分34 秒，云南省大理州漾濞县发生6.4 级地震，震源深度为8 km。根据中国数字化强震动观测网络（CDSMON）的观测结果，此次地震共有完整三分量地震动记录264条（88组）。为了分析此次地震的反应谱特征是否与文中预测模型相符，文中根据漾濞地震记录的反应谱值和模型预测值计算两者的残差，检验、分析残差并从中得到漾濞地震的反应谱特征及其与区域地震的差异，从而为该地区的震害评估、地震动影响场的估计以及抗震设防等提供参考，并通过计算模型预测的准确率得到文中模型能较好的预测漾濞地震的结论。

1 区域地震动数据与地震动预测模型

1.1 川滇地区地震动数据

文中选取了2007 年到2017 年川滇地区水平方向两分量地震动数据共计4 458 条，面波震级（MS）在4 级到7 级之间，震中距在200 km 以内，图1 给出了所有记录的震中和强震动台站的分布图，这些记录的震级与震中距的分布如图2所示。文中对所有地震动记录进行了基线校正和滤波（0.1～35 Hz）处理，分别采用了基线修正法和4阶非因果Butterworth滤波方法处理数据，以东西（EW）和南北（NS）方向加速度峰值的几何平均值作为水平方向的反应谱值。

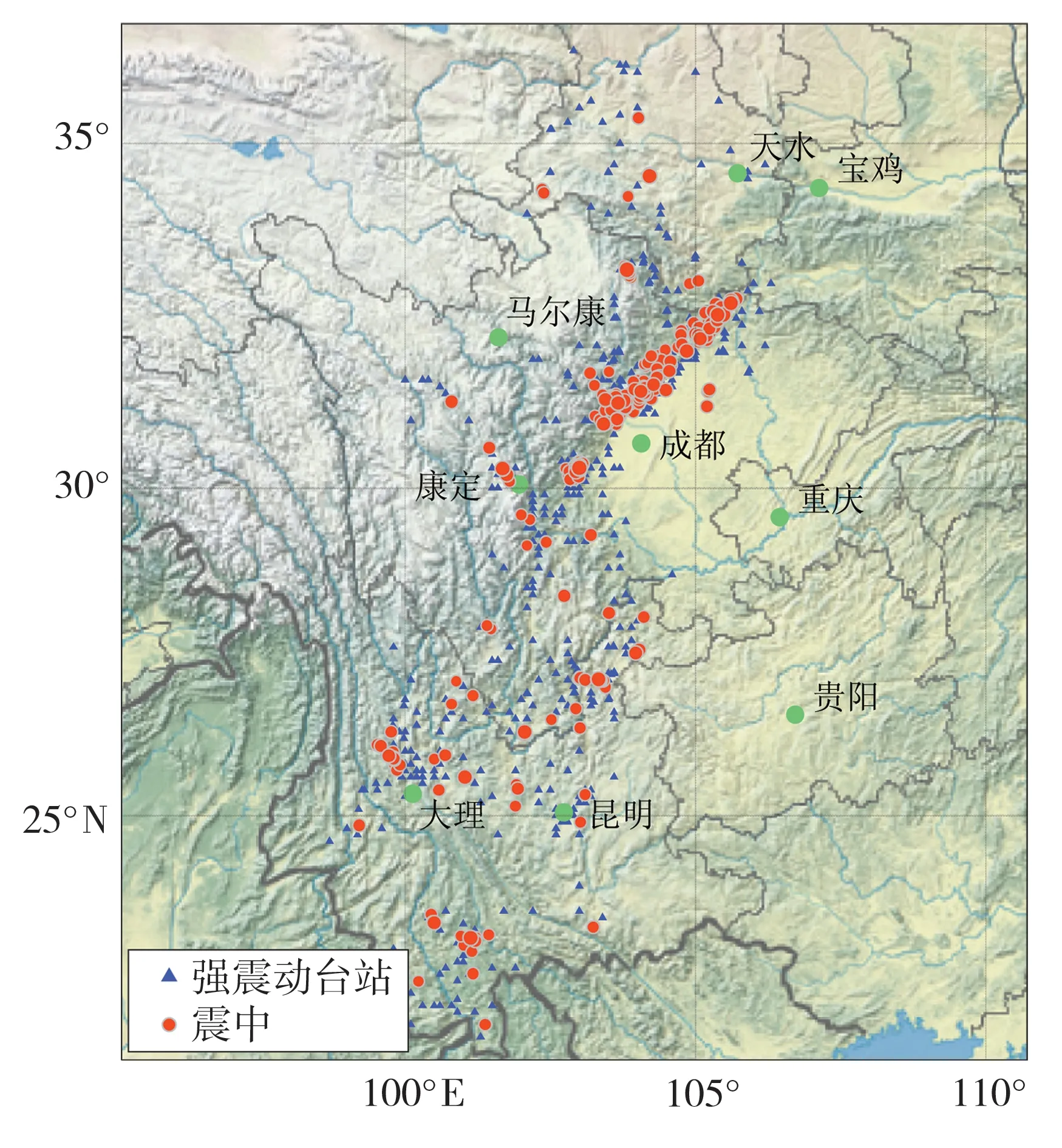
图1 本文选取记录的震中与强震动台站分布Fig.1 The distribution of epicenters and strong motion stations used in this study

图2 选取地震动数据的震级与震中距的关系Fig.2 The relationship between magnitude and epicentral distance of selected ground motion data

1.2 地震动预测模型

基于川滇地区实际地震动数据并综合比较多个地震动预测模型后，文中采用简化的OSM04［7］预测模型。由于缺乏精确的相关断层信息，文中用震中距代替原模型中的断层距；所有选取地震动的场地条件均为土层场地，可将原模型中的场地条件项视为常数。简化预测模型如式（1）：

式中：Y是PGA 或是阻尼比为5%的单自由度结构在不同自振周期下对应的峰值加速度值（Sa）；MS是面波震级；Repi是震中距；C1、C2、C3、C4和C5均为模型系数。

2 预测模型结果与残差分析

2.1 预测模型结果

文中用随机效应方法［6］计算预测模型的系数，随机效应回归将总残差分为事件间残差和事件内残差，对于某一周期下，事件间残差代表某一次地震反应谱平均值与所有地震反应谱平均值的差值，而事件内残差代表某一次事件内某条记录反应谱值与这一次事件的反应谱平均值的差值，具体公式如式（2）：

模型系数的回归结果如表1所示，其中σ是事件间残差的标准差，τ是事件内残差的标准差，而总标准差等于σ与τ的平方和的算术平方根。

表1 预测模型系数表Table 1 The coefficient of prediction model

图3 给出了在不同震级下预测模型的PGA 随距离的衰减曲线以及对应震级下真实地震动数据的PGA与震中距之间的分布散点图，从图中可以看出真实数据的PGA 散点图与文中预测模型的PGA 曲线基本相符，因此文中的预测模型能较好的拟合川滇地区实际地震数据的PGA。图4 是震中距分别为10、50、100 和200 km时预测模型在不同震级下的加速度反应谱曲线。

图3 PGA预测值与震中距的关系及PGA真实值的散点图Fig.3 The relationship between predicted PGA value and epicentral distance，and the scatter plot of true PGA value

图4 震中距为10、50、100、200 km时不同震级对应的反应谱曲线Fig.4 Response spectra of different magnitudes at epicentral distances of 10，50，100 and 200 km

2.2 残差分析

采用随机效应回归模型计算预测模型的系数时，残差分为事件间残差和事件内残差。图5 给出了PGA和周期为0.2、1、3、5、10 s 时的事件间残差随震级的分布，从图中可以看出在PGA 和其他几个周期下事件间残差随震级的增加在0附近均匀分布，这表明事件间残差与震级并没有明显的相关关系。但在图5中，PGA和周期为0.2 s 时的事件间残差相比其他周期时的残差分布会更加分散。在比较所有不同周期时的事件间残差随震级的分布后发现：当周期小于等于0.2 s时（包括PGA），事件间残差的分布更加分散，这是因为根据所选择的预测模型及回归得到的模型系数，T=0.2 s 时的反应谱值与PGA 值基本相等，当周期大于0.2 s 后，反应谱值随着周期增大而减小，这就导致T＞0.2 s 时事件间残差整体相对更小，因此这些周期的事件间残差的分布更靠近残差为0的坐标轴。

图5 不同周期下事件间残差随震级的分布图Fig.5 The distribution of inter-event residual with magnitude in different periods

图6 和图7 分别给出了PGA 和周期为0.2、1、3、5、10 s 时的事件内残差随震级和震中距的分布。从图中可以看出，事件内残差的平均值均在0 附近，而且大部分事件内残差的95%置信区间包含有0，因此事件内残差没有随震级或者距离变化而呈现明显的变化趋势。

图6 不同周期下事件内残差随震级的分布图Fig.6 The distribution of intra-event residual with magnitude in different periods

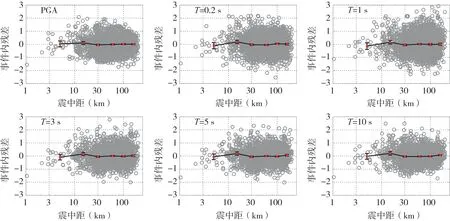
图7 不同周期下事件内残差随震中距的分布图Fig.7 The distribution of intra-event residual with epicentral distance in different periods

通过分析实际地震动数据的反应谱值与预测模型之间的残差，可以看出随着震级或震中距的增加，该残差没有显著的趋势，因此文中的地震动预测模型能够很好的拟合川滇地区已有的地震动数据。

3 地震动预测模型的对比分析

为了分析文中预测模型的合理性，将文中的地震动预测模型与俞言祥等［1］通过转换方法得到的中国西部地区水平向加速度反应谱、王玉石等［5］得到的川滇地区水平向强地震动衰减关系进行对比，结果如图8所示。

图8 不同震级、距离下预测模型对比图Fig.8 Comparison of prediction models at different magnitudes and distances

图8 （续）Fig.8 （Continued）

从图8 可以看出：当周期小于0.1 s 时，文中预测模型与俞言祥等的中国西部长轴衰减关系的预测值相当，当周期在0.1 s 和0.3 s 之间时，文中预测模型的预测值介于俞言祥等的中国西部长轴衰减关系和短轴衰减关系之间，而当周期大于0.3 s 时，文中预测模型要低于俞言祥等的中国西部短轴衰减关系；当周期小于0.3 s 时，文中预测模型比王玉石等的川滇地区地震动衰减关系的预测值小，两个模型的差值在震级较小时相对较大，并随着震级的增加而逐渐减小，当周期大于0.3 s时，文中预测模型要略大于王玉石等的川滇地区衰减关系的预测值，并且两者随着震中距的增加而逐渐接近。

文中模型选取的川滇地区地震动数据集中，震级为4～5 级的数据所占的比例较大，而王玉石等的衰减关系选取的地震动数据震级在5级以上，受此影响，文中预测模型在震级较小时（MS＜5）短周期反应谱值要小于王玉石等的衰减关系，而在周期大于0.3 s时文中预测模型略大于王玉石等的衰减关系的原因可能是由数据集以及预测模型公式的差异所导致。

4 预测模型对漾濞地震的适用性

为了验证文中地震动预测模型对漾濞地震的适用性，文中根据预测模型的适用范围从漾濞地震的前震、主震和余震数据中选取了有完整三分量且波形正常的36组地震动，详细的地震信息如表2所示。

表2 漾濞地震信息Table 2 The information of Yangbi earthquake

将所选地震动进行基线校正和滤波处理后取水平两分量加速度峰值的几何平均值为真实值，再根据式（1）和表1的系数得到文中模型的预测值，最后残差的计算公式如式（3）：

式中：Satrue是加速度反应谱的真实值；Sapredicted是加速度反应谱的预测值；Ti是周期。

如图9 所示，图9（a）是此次地震的PGA 与预测模型的残差随震级分布的散点图，图9（b）是PGA 的残差随震中距分布的散点图，而图9（c）是除PGA以外其他周期的残差的散点图，红色实线是各周期残差的均值，而红色虚线则是各周期残差的均值加（减）一倍标准差（漾濞地震残差的标准差）。从图9（a）和（b）中可以看出，文中模型对漾濞地震的PGA具有较好的预测效果，漾濞地震PGA的残差随震级没有明显的趋势，但是残差随震中距的增加存在减小的趋势，特别是当震中距大于130 km 时，PGA 的残差均小于0，这表明漾濞地震的PGA 在远场要小于文中模型的预测值，与川滇地区其他同震级的地震相比，漾濞地震的峰值加速度随震中距的增加而衰减得更快。在图9（c）中，漾濞地震反应谱值与预测模型的残差均值在短周期（T＜0.3 s）内基本在0附近，但是在中长周期（T＞0.3 s）残差均值存在大于0的现象且偏差相对较大，而这一现象可能是由震源机制和场地条件的差异造成的。

图9 PGA和各周期处残差散点图Fig.9 The scatter diagram of PGA and other periods'residual

理想状况下真实观测值与模型预测值的残差随预测模型的自变量的分布可以变换为均值为0、标准差为1的标准正态分布［8］，因此对于同源地震数据，地震动预测模型在各周期点处的残差也需要服从标准正态分布［9］。为了确定文中地震动预测模型对于漾濞地震数据的适用性，文中采用K-S（Kolmogorov-Smirnov）假设检验来判断各周期点处真实反应谱值与模型预测值的残差是否符合标准正态分布，显著性水平设置为0.01，计算不同周期下残差的p值，若在周期为T时得到的p值高于显著性水平（0.01），则接受原假设，即认为在该周期处的残差符合标准正态分布。如图10 所示，图10（a）是漾濞地震数据与文中模型的残差通过K-S检验计算的p值随周期变化的曲线（漾濞地震PGA的残差p值为0.308 7），可以看出当周期小于0.4 s时，残差的p值均大于0.01（T=0.15 s 除外），这表明这些周期处的残差符合均值为0，标准差为1 的正态分布；图10（b）、（c）、（d）是不同周期处残差和标准正态分布的累积分布函数（CDF）的对比图，这两个CDF曲线分别对应图中的蓝色曲线和红色实线，而图中的红色虚线则是标准正态分布在0.01 的显著性水平下K-S 检验的边界，若残差的CDF 曲线在K-S 检验的拒绝界限以内（即蓝色曲线在两条红色虚线之间），则残差符合标准正态分布。

从图9 和图10 中可以看出，文中预测模型在周期小于0.4 s 时基本能够很好的预测此次漾濞地震的反应谱值，而当周期大于0.4 s 时，文中模型的预测值与此次地震的反应谱值存在较为明显的偏差，这表明此次地震的反应谱在短周期（T＜0.4 s）范围内与川滇地区其他同震级地震基本没有差别，但是在中长周期（T≥0.4 s）范围内反应谱值明显存在高于文中模型预测值的趋势，因此与川滇地区其他同震级地震相比，此次地震中长周期的地震动强度相对较高，而这可能会对该地区的长周期建筑物存在一定影响［10-11］，这也与陶冬旺等［12］得到大理某高层建筑在漾濞地震主震作用下加速度反应谱在0.5～1 s 随周期的增加衰减较慢的结论一致。

图10 残差的p值与周期的关系曲线和T=0.05、0.35和1 s时残差的CDF曲线Fig.10 The relationship between the residual's p-value and the period，and the CDF curves of residual at T=0.05，0.35 and 1 s

为了分析将文中模型用于预测漾濞地震反应谱值的准确率，分别比较此次地震的真实值与模型预测值的残差在各周期处与文中预测模型的2 倍（1 倍）标准差的大小，计算残差在预测模型正负2 倍（1 倍）标准差以内的百分比即为模型预测的准确率，文中模型预测漾濞地震的准确率如图11所示。从图11可以看出，1倍标准差以内的模型预测准确率在短周期基本大于50%，而在中长周期的准确率在30%～50%之间，这也与图9 中残差散点图相符；而2 倍标准差以内的模型预测准确率基本在80%以上，因此文中地震动预测模型能较为准确的预测此次漾濞地震。

图11 各周期处模型预测准确率曲线Fig.11 The accuracy of model prediction at each period

5 结论

文中基于川滇地区已有的地震动数据通过随机效应回归模型得到该区域的地震动预测模型，并根据此次漾濞地震的数据分析该模型对此次地震的适用性，得到的结论如下：

（1）文中的川滇地区水平向地震动预测模型在周期小于0.3 s 时低于王玉石等的川滇地区衰减关系，且此差值随震级的增大而减小，这可能是由于选取数据集的差异造成的；在周期大于0.3 s时，文中地震动预测模型略高于王玉石等的川滇地区衰减关系，略低于俞言祥等的中国西部短轴衰减关系。

（2）漾濞地震的PGA 与川滇地区其他同震级地震基本相同，且PGA 与模型预测值的残差随震级增加没有明显趋势，但是残差随震中距增加存在降低的趋势，这表明漾濞地震存在PGA 随震中距的增加而衰减得更快的特点。

（3）文中地震动预测模型在两倍标准差以内对此次地震的预测准确率基本在80%以上，这表明该模型能较好的预测此次地震；通过残差分析可知，此次地震反应谱值在短周期（T＜0.4 s）范围内与文中模型预测值基本相同，但是在中长周期（T≥0.4 s）范围内存在高于文中模型预测值的趋势，这表明与川滇地区其他同震级地震相比，此次地震中长周期的地震动强度相对较高，这可能会对该地区中长周期建筑物的抗震设防提出更高的要求。

致谢：感谢中国地震局工程力学研究所“国家强震动台网中心”为本研究提供数据支持。