基于红外光谱分析法的中药材种类与产地判别
谢晓敏
(川北幼儿师范高等专科学校 初等教育系,四川 广元 628017)
中药是成分复杂的混合物,其品质鉴别与质量控制一直是科研和实践领域关注的重点。产地是中药材道地性的主要指标,对于药材品质鉴别尤为重要。相比较而言,利用红外光谱技术进行中药材品质鉴别更直接、快速,也更准确[1]。由于不同中药材表现的光谱特征差异较大,即使来自不同产地的同一药材,因其无机元素的化学成分、有机物等存在差异性,在近红外、中红外光谱的照射下,也会表现出不同特征,因此可利用这些特征鉴别中药材的种类及产地。不同种类中药材呈现的光谱区别较明显,故中药材种类鉴别相对比较容易。然而,不同产地的同一药材在同一波段内光谱较接近,使光谱鉴别误差增大,而有些中药材近红外光谱区别较明显,有些则中红外光谱区别较明显,故分析、提取红外光谱特征显得尤为重要。
1 问题的提出
1.1 数据来源
数据来源于2021年高教社杯全国大学生数学建模竞赛E题附件2、3、4,且假设所获数据真实有效,未受空气湿度、光照强度等因素干扰。
1.2 问题提出
问题一:附件2给出了673个药材从551到3 998连续3 448个波数的中红外吸光度信息,已知其中658个药材来源于11个产地,15个药材产地信息未知,需要根据已知判别其产地。
问题二:附件3给出了255个药材从552到3 999连续3 498个波数的中红外及从4 004到10 000连续5 996个波数的近红外吸光度信息,已知其中245个药材来源于17个产地,10个药材产地信息未知,需要根据已知判别其产地。
问题三:附件4给出了399个药材从4 004到10 000连续5 996个波数的近红外吸光度信息,其中:A类药材97个,B类药材102个,C类药材57个,143个药材未知类别,需要根据已知判别其类别;349个药材来源于16个产地,50个药材产地信息未知,需要根据已知判别产地,将所给编号药材的类别与产地鉴别结果填入表格。
1.3 问题分析
上述三个问题都需要充分挖掘已知信息,剔除信息量较少的数据,降低原始数据维数,掌握不同产地和种类药材的特征及其差异性,选择恰当的判别方法,最终正确鉴别出未知产地及类别,并交叉验证其判别法的正确率及所用判别法的优劣。
2 数据预处理
以附件2为例,说明对原始数据所使用的降维处理方法。
2.1 方法一
在Excel中利用STDEV函数对附件2数据计算每个波数下吸光度的标准差,一些波数的标准差完全相等,认为这些波数贡献了相同的吸光度信息,可在Excel中利用删除重复项功能,除去标准差重复的波数,保留标准差不相同的波数,可将已知数据从3 448列降至1 789列。虽然剩余波数的标准差不同,但很多仍接近,因此,对所剩波数的标准差保留3位小数,再次使用删除重复项操作,将1 789列数据降至181列。
随机选取11个产地中的任一药材进行数据处理并对比,结果见图1。

图1 方法一数据处理前后图像对比
观察图1(a)发现,11个产地药材的光谱趋势大体一致,但各药材的最大吸光度、峰高、峰宽、峰差不同。对比图1(a)(b)可看出,数据预处理后不同产地的图像间区别更明显,更容易辨别出产地,表明数据预处理方法有效。
2.2 方法二
对附件2中每i个连续波数的吸光度求平均值,最后不足i的剩余波数也同样求均值,以此降低数据的维数。维数Vi计算公式为
当i=10、15、20、25、30时,原始数据维数将由3 448分别降至345、230、173、138和115。选择和图1相同编号的中药材降维数据绘制图像如图2所示。
从图2可看出,数据预处理后图像的走势和原始数据一致,可见此数据预处理方法最大限度保留了原始数据的单调性特征。

图2 方法二数据预处理后连续i个波数对应的平均吸光度
方法一、方法二均可对原始数据简单降维,降维后还可进行一阶导数和二阶导数运算,通过求导可突出谱线的变化部分,消除各谱线基线不同带来的影响[2]。
3 问题解决
3.1 附件2产地判别
3.1.1 样本均衡性分析
为防止出现过拟合现象,需对样本的均衡性进行分析。附件2中658个已知产地信息的药材产地分布情况统计如表1。

表1 11个产地的药材数量
从表1可看出,每个产地的样本数相差不大,可以不考虑对样本数进行统一。
3.1.2 判别分析综述
判别分析是对未知类别样本进行归类的一种方法。判别分析的研究对象已有了分类,只需根据抽样样本建立判别公式和判别准则,然后判别样品类别。用数学语言表达为:设有n个样本,每个样本测量p项指标,已知每个样本属于k个类别(或总体)G1,G2,…,Gk的某一类,分布函数为F1(x),F2(x),…,Fk(x),找到一种判别函数,使得这一函数具有某种最优性质,能把属于不同类别的样本点尽可能区分开,并对同样测得p项指标的新样本进行分类。
判别分析的主要方法有距离判别法、Fisher判别法、Bayes判别法和逐步判别法。
3.1.3 线性判别模式
设有k个总体G1,G2,…Gk,其均值和协方差矩阵分别为μ1,μ2,…μk和∑1,∑2,…∑k,而且∑1=∑2=…=∑k=∑。
假定Gi~Np(μi,∑),i=1,2,…,k,即各组的先验分布均为协方差矩阵相同的p元正态分布。对于一个新的样品X,要判断其来自哪个总体。
运用贝叶斯判别法思路,先计算k个总体按先验分布加权的误判平均损失hj(x),
其中:f(ix),i=1,2,…,k为每一个总体Gi的分布密度函数;来自总体Gi的样品被错判为来自总体G(ji,j=1,2,…,k)时所造成的损失记为且为样品来自总体Gi的先验概率。
然后,再比较这k个误判平均损失h1(x),h2(x),…,hk(x)的大小,选取其中最小的,判定样品X来自该总体。
3.1.4 判别方法选择
调用MATLAB统计工具箱提供的classify函数,可进行先验分布为正态分布的贝叶斯判别,调用格式如下:
其中:type参数选择 “linear” 线性判别模式;sample是带判别的样本数据;trainning是已知分类结果的样本数据矩阵,用于构造判别函数,其每一行对应一个观察,每一列对应一个变量;sample和training具有相同的列数;参数group是与training相应的分组变量,group和training具有相同的行数,group中的每个元素指定了training中相应的观测值所在的组。
3.1.5 交叉验证
数据处理和判别方法的选择有效性直接决定了判别结果的正确率,为了证明判别的优劣,需进行交叉验证。
本文采用留一法进行交叉验证[3]。留一法是机器学习中对学习器进行评估的一种方法,属于交叉验证法的一个特例。假定数据D中有m个样本,分成m个小数据集,即每个样本都是一个数据集,每次使用其中一个作为测试集,其余m-1个为训练集,重复检验m次,统计被错分的样本数k,最后用k/m作为错误率的估计值,则正确率的估计值为1-k/m。此法使用的训练集与初始数据集相比只少了一个样本,在绝大多数情况下,留一法中被实际评估的模型与期望评估的D训练所得的模型很相似。因此,留一法评估结果往往比较准确。但留一法最大的缺陷在于,数据集较大时,训练m个模型的计算量可能很大。本文数据集并不大,故交叉验证选择留一法可行,能取得较好结果。
运用方法一处理数据不求导、求一阶导、求二阶导后,用留一法交叉验证计算所得准确率分别为98.02%、97.87%、98.02%。未知产地信息的判别情况均相同,如表2所示。

表2 附件2未知产地编号药材的产地判别信息
运用方法二处理数据后,无论求一阶还是二阶导,都不能提高判别的准确率,因此,直接运用降维后的数据来判别。用留一法交叉验证计算准确率,当i=10、15、20、25、30时,准确率分别为98.18%、98.02%、97.26%、97.57%、96.96%。无论i取何值,未知产地信息的判别情况均相同,且与方法一表2中判别结果一致。
3.1.6 性能评价
(1)运用方法一处理数据不求导和求二阶导后,判别的准确率相同,其中658个药材有13个判别错误,其余全部判断正确。判别错误的药材编号一样,且判别错误的产地也相同,如表3所示。

表3 判别分析错误情况表
对11个产地的判别准确率分析,结果见表4。由表4可见,判别准确率最低为94%,2、4、5号产地全部判别正确,综合判别准确率为98%。因此,表2中对未知产地的判别结果准确可靠。
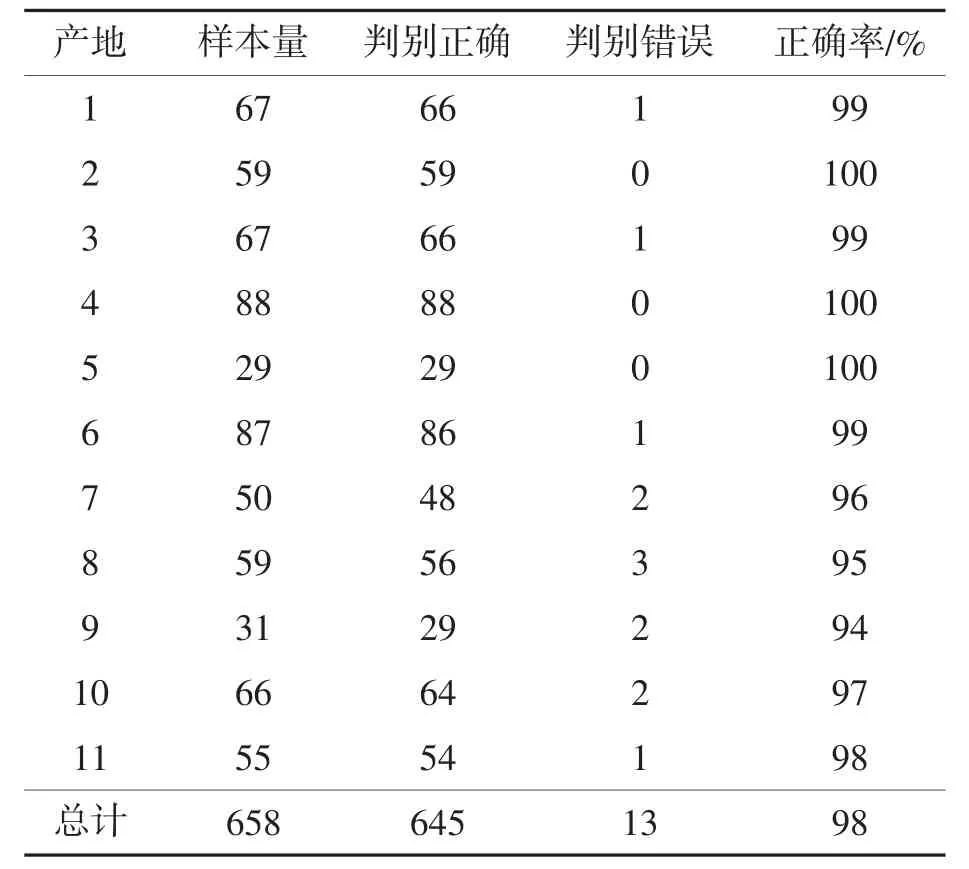
表4 各产地的评价指标
(2)运用方法二处理后数据不求导,当i=10时,交叉验证的准确率最高,总计658个药材中12个判别错误,其余全部判断正确。判别错误的情况如表5所示。

表5 i=10时判别错误情况
对11个产地的判别准确率分析结果如表6。由表6可见,判别准确率最低为95%,5、9、11号产地全部判别正确,综合判别准确率为98%。因此,表2中对未知产地的判别结果是准确可靠的。
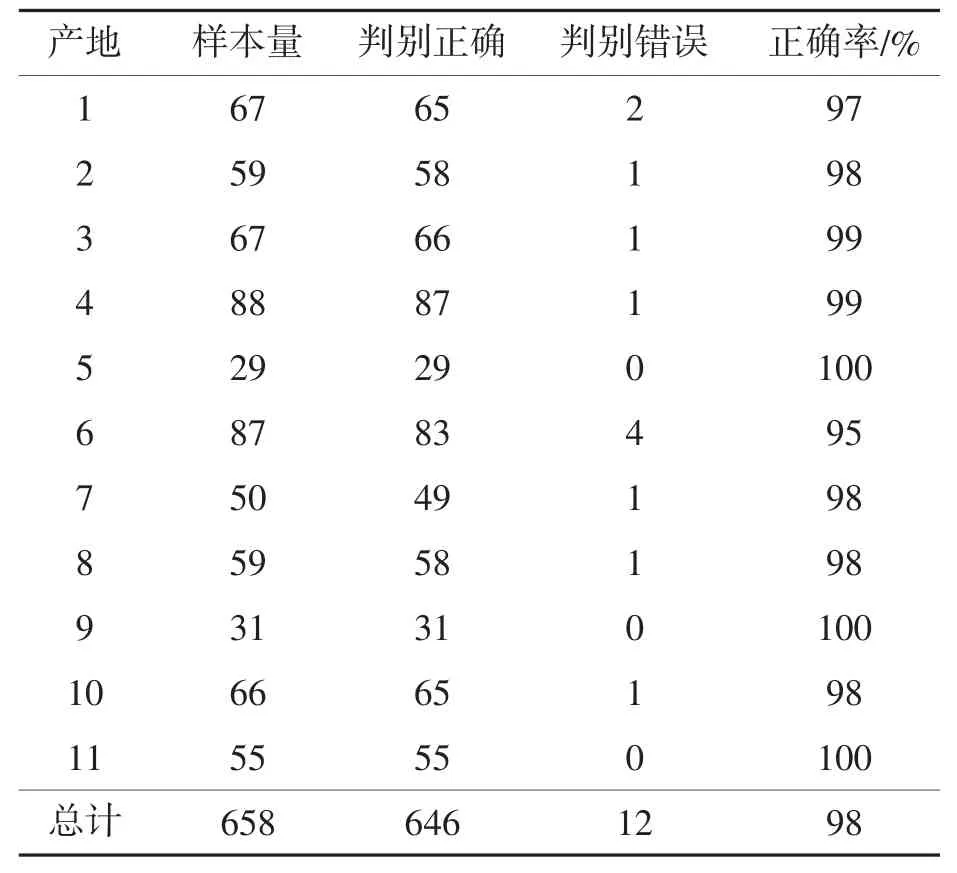
表6 各产地的评价指标
3.2 附件3产地判别
附件3中有中红外、近红外两种光谱信息,先用近红外,再用中红外,最后将近红外和中红外两种光谱结合起来进行判别分析[4]。
3.2.1 样本均衡性分析
17个产地药材数量信息如表7。从表7可看出,每个产地的样本数相差不大,可不考虑对样本数进行统一处理[5]。

表7 17个产地的药材数量信息
判别和交叉验证方法与3.1相同。
3.2.2 结果分析与性能评价
运用方法一处理近红外数据,将数据降至215维,不求导、求一阶导、求二阶导后进行留一法交叉验证,计算的准确率分别为68.57%、69.80%、71.02%,表明判断正确率较低。
运用方法一处理中红外数据,将数据降至86维,求二阶导后留一法交叉验证,计算的准确率为97.14%,判断正确率较为理想。
运用方法一将近红外数据降至25维,与中红外数据86维合并成111维,求二阶导并交叉验证,计算准确率达98.37%。
各产地的评价指标见表8,通过对17个产地的判别准确率分析,发现2、3、10、17号产地的判别准确率为93%,其余全部判别正确(准确率为100%),综合判别准确率为98%,可见此法可用于判别未知产地。

表8 各产地的评价指标
针对近红外光谱数据,i分别取50、55和60,运用方法二处理后数据不求导,交叉验证准确率分别为97.14%、97.55%和96.73%。
针对中红外光谱数据,i分别取20、25和30处理后数据不求导,交叉验证准确率分别为97.96%、98.37%和97.96%。
将附件中近红外和中红外数据仅作合并处理,i分别取80、90、95和100,数据不求导,交叉验证准确率分别为97.55%、97.96%、97.55%、97.96%和97.55%。
综上所述,无论运用方法一还是方法二,最终附件3中未知产地编号药材的产地判别情况如表9。
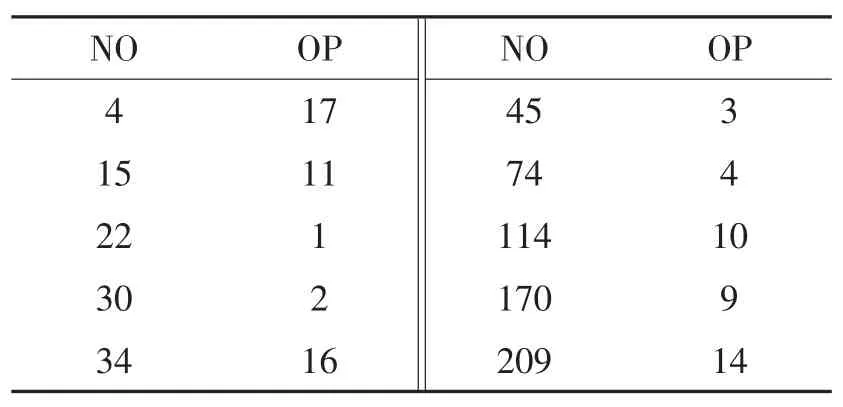
表9 附件3未知产地编号药材的产地判别信息
3.3 附件4判别分析
相比较而言,药材的类别容易判断,故可先判断类别再判别产地。
3.3.1 判别药材的类别
首先,对已知类别药材数据信息进行统计,如表10所示。

表10 3种类别药材数量信息
运用方法一处理数据,对标准差保留3位有效数字,然后删除重复项,把数据从5 996维降到97维。不求导、求一阶导、求二阶导后判别,再用留一法交叉验证,计算的准确率均达100%,且对未知类别药材的判别结果均一样,因此,可采用此法对未知类别的药材进行类别判别。
运用方法二处理数据,当i分别取30、40、50、60时,判别后用留一法交叉验证,计算准确率均为100%,且对未知类别药材的判别结果均相同,与方法一的判别结果也完全一致,即未知类别的药材判别准确率能达100%。
3.3.2 判别药材的产地
首先,对已知产地的药材数据信息进行统计,如表11所示,其中已知总计349,未知50。

表11 16个产地的药材数量信息
运用方法一处理近红外数据,将数据降至97维,不求导、求一阶导、求二阶导后,留一法交叉验证,计算准确率分别为84.53%、85.39%、84.81%,判断正确率较低。
运用方法二处理数据,当i分别取50、60、70、80、90时,判别后用留一法交叉验证,计算准确率分别为91.4%、92.26%、92.84%、94.27%、94.27%。对未知产地药材的判别结果一致,且与方法一的判别结果也完全相同。
显然,运用方法二处理数据所得结果判别更为准确,效果更优。未知50个编号产地药材判断结果最多有4个不同,i为80和90时,只有2个判断结果不同。
以i=90为例,对各产地判断情况进行分析,结果如表12。无论采用何种方式处理数据,最终求得所给出编号的药材类别与产地的鉴别结果都相同,如表13所示。

表12 各产地的评价指标

表13 给出编号的药材类别与产地鉴别结果
从上述研究可看出,利用红外光谱分析法鉴别中药材的种类和产地,判断较为准确,效果较好。

