狮群优化核极限学习机的分类算法
刘新建,孙中华
(武汉烽火信息集成技术有限公司,湖北 武汉 430074)
0 引言
图像分类是图像领域的研究热点之一,研究者对于不同场景的图像采用不同的算法进行研究。极限学习机(Extreme Learning Machine,ELM)有效避免了传统前馈神经网络训练的劣势,基于学习速度快、泛化性能好等优势应用于图像分类领域。文献[1]采用改进蝙蝠算法优化极限学习机进行图像分类,提高分类准确率的基础上加快了分类速度;文献[2]采用萤火虫算法(Firefly Algorithm,FA)优化极限学习机对遥感影响进行分类,FA 优化算法高于传统的遗传算法(Genetic Algorithm,GA)和粒子群算法(Particle Swarm Optimization,PSO)优化方法;文献[3]采用鱼群算法优化极限学习机,可获得更好的分类效果;文献[4]采用局部信息保持极限学习机,在分类性能上优于KELM 算法;文献[5]、[6]采用多核多特征进行重构ELM,提高了准确性和完整性。综上,较ELM,采用群智能优化算法可获得更好的分类效果。KELM 采用核函数来取代ELM 的内积运算,增加了函数逼近能力,提高了非线性分类能力。文献[7]采用核极限学习机应用于脉象分类问题,较反向传播算法(Back Propagation,BP)和支持向量机算法(Support Vector Machine,SVM)提高了分类准确性。文献[8]采用核极限学习机可获得乳腺良恶性肿块样病变数据的分类准确率。
文献[9]指出LSO 比PSO 算法具有收敛速度快、精度高的特点,可获得全局最优解。文献[10]、[11]指出狮群算法优化传统算法,可获得更高精度。本文在KELM 良好的分类性能基础上,结合LSO 的寻优能力,提出LSO优化KELM 算法(简称LKELM),并采用UCI 数据集进行仿真测试,以检验分类精度的提高程度。
1 KELM 算法
1.1 ELM
对于给定的训练样本集以及前馈网络的激活函数与隐含层节点数,采用ELM 训练的步骤如下:
(1)随机给定隐含层连接权值(ai,…,bi),i=1,…,L,并计算其输出矩阵H,如式(1)所示:

(2)求解输出权值β 的最小二乘范数解,如式(2)所示:

其中,I 是单位矩阵,C 是常数,Y 是期望矩阵。
由此可得出,采用ELM 的分类公式如式(3)所示:

1.2 KELM
根据ELM 的输出矩阵H,h(xi)可视作xi的非线性映射。当映射关系未知时,可通过构造核函数来替代HHT,如式(4)所示:
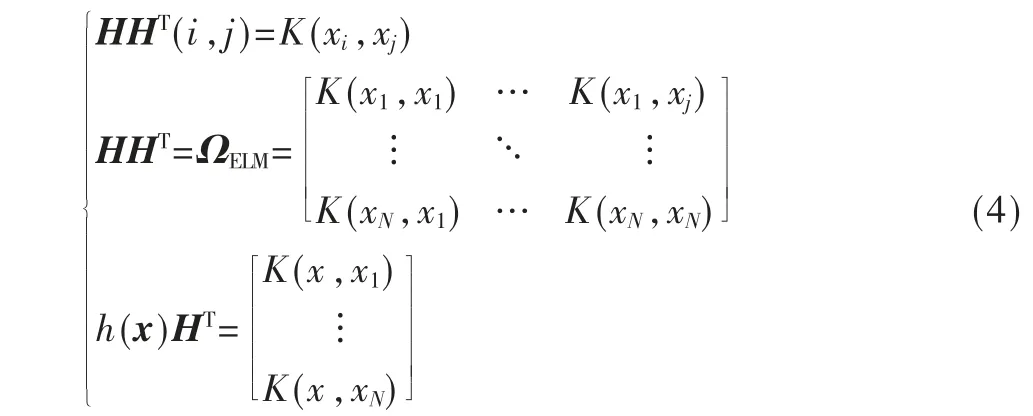
那么,将式(4)带入式(3)可得式(5):

由此可见,KELM 在ELM 的基础上引入核函数,增强了其非线性分类能力,而核函数的选择影响其分类效果[12]。KELM 的推演过程可见文献[13]。
2 LSO 算法
2.1 基本原理
LSO 寻优主要来源于狮王、母狮和幼狮的社会行为。其中,狮王社会行为包括保护和分配食物给幼狮,面对自身种群的优胜劣汰机制以及外来群种的挑战来获得首领的地位;母狮主要负责养育幼狮并根据猎物踪迹范围来猎食,猎食范围从大范围勘探直至收缩范围;幼狮在狮王和母狮的保护下历经索取食物、学习捕猎、被狮王驱逐,公狮则挑战原有狮王地位。
LSO 的寻优思想为:从初始位置(待寻优空间),狮王处于最佳适应度值的位置;在捕猎狮(一定比例)通过相互配合捕猎获得比狮王现有猎物更优质的猎物,狮王将其占有;幼狮在狮王和母狮的护佑下进食和学习捕猎,即使在被驱赶后可凭借记忆向待寻优空间靠近,不断重复搜寻,最终可获得目标函数最优值。
2.2 相关参数
成年狮所占比例因子β:在整个狮群中,如果成年狮所占比例越大,则幼狮占比越少。幼狮位置更新多样性,可增加种群的差异性,从而提高算法的搜索能力。成年狮为0~1 区间的随机值,为加快收敛速度,一般小于0.5。
母狮移动范围扰动因子αf:在快取得全局最优解的位置附近通过增加扰动因子来增强局部搜索能力,使得母狮的捕猎范围能够由大范围逐步缩小,直至趋于0 的微小值。增加母狮移动范围扰动因子可有效避免早熟问题,使得能够在全局和局部搜索能力间获得均衡,可获得最优解,如式(6)所示:

幼狮移动范围扰动因子αc:幼狮在索取食物和学习捕猎活动均会在一定范围内,幼狮移动范围扰动因子可有效控制该范围,该范围亦从大到小,呈线性下降趋势,表达式如式(7)所示:

2.3 算法原理
假设在D 维空间中由N 个狮子组成狮群,成年狮子数量为nleader,其范围如式(8)所示:

其中,仅有的一头公狮为狮王,其余则为母狮。那么,第i(1≤i≤N)个狮子的位置如式(9)所示:
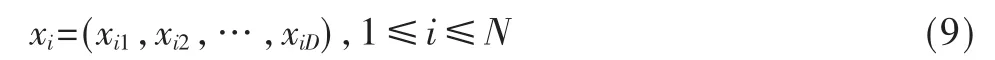
成年狮的数量为nleader=[Nβ],幼狮数量为N-nleader。狮王、母狮以及幼狮的位置移动分别如式(10)~式(12)所示:

3 本文算法
KELM 有效避免了ELM 算法的随机初始化问题并适用于小样本的非线性分类问题,其训练速度快,泛化性能好,且具有较好的鲁棒性,广泛应用于数据分类及预测问题。本文采用高斯径向基核函数,其属于局部核函数,优势在于局部学习能力强,但全局泛化能力差,易陷入局部最优解。为提高其全局寻优能力,可结合全局寻优的相关算法。为此,采用LSO 智能算法来提升其全局泛化能力,从而兼顾全局和局部寻优能力。在迭代运算中,基于不同狮子的不同移动位置规则,个体最优的被保留,否则将被适应度高的个体所替换。在LSO 算法中,采用KELM 计算的测试准确率作为其适应度函数,用以判断全局最优位置和历史最优位置,从而获得全局最优解。
优化思想:以适应度函数作为评价优化算法分类高低函数,适应度值越高表明其分类准确率越高,其倒数可反映优化算法的收敛速度。在初始化过程中计算适应度值,确定最优位置为狮王位置以及历史最优位置作为母狮及幼狮的位置;在迭代过程中,不同类型的狮子按照式(10)~式(12)更新位置,并计算适应度值,此适应度值与历史最优适应度值有所变化,从而寻求最优适应度值。
本文算法的步骤描述如下:
(1)训练集与测试集在训练前先采用归一化处理;
(2)建立KELM 的神经网路结构,确定核函数;
(3)确定LSO 相关参数,如种群数量、最大迭代次数、维度、成年狮占比等;
(4)狮群种群初始化,计算初始适应度值等;
(5)设定适应度函数,根据迭代过程中的移动位置不断获取最优适应度值;
(6)判断迭代次数,如达到则终止,否则进行执行步骤(5)。
4 实验分析
实验采用部分UCI 数据集,其数据包括类别信息及特征数据。其中,Wine 数据集包括3 类数据178 条记录(1 类59 个样本,2 类71 个样本,3 类48 个样本),每条记录包含13 种属性特征。
采用MATLAB 2013a 软件测试。KELM 采用径向基核函数,迭代次数为50,初始种群为30,维度为2,训练样本为分别选择36、89。LKELM 的分类效果对比分别如图1、图2 所示。
由图1、图2 可知,针对不同数量的训练样本,在迭代次数很低的情况下,采用LKELM 可快速获得较高的分类预测精度。训练样本为36 时,LKELM 分类精度为0.791 67,KELM 分类结果为0.777 67,精度差异为0.014;训练样本为89 时,LKELM 分类精度为0.825 4,KELM 分类结果为0.814 4,精度差为0.011。为进一步对比不同测试集的分类效果,其实验结果如表1 所示。
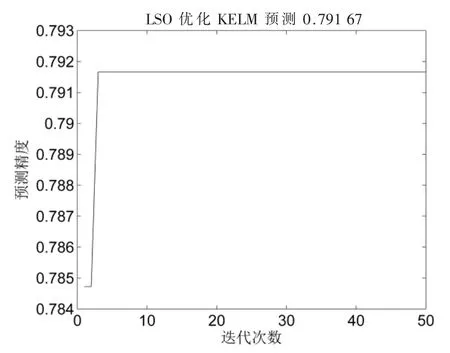
图1 LSO 优化KELM 分类效果(训练样本36)

图2 LSO 优化KELM 分类效果(训练样本89)
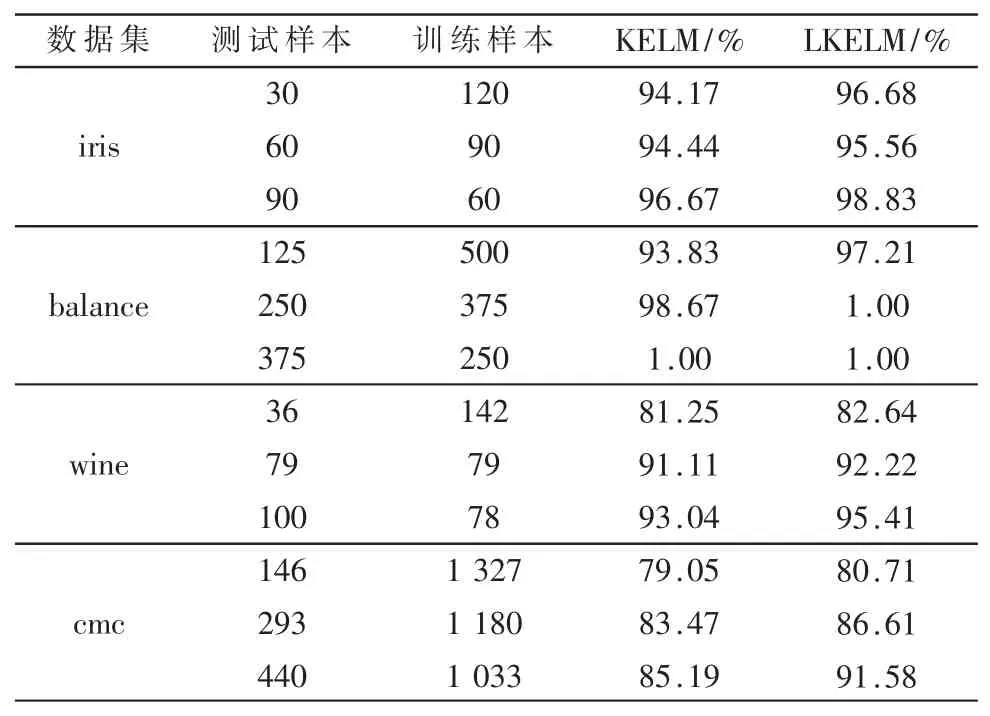
表1 不同测试集不同训练样本的分类对比
UCI 测试集较多,本文以表1 中4 种数据集为例进行分析。通过表1 数据可知,LKELM 比KELM 在分类精度上均有提高。这也表明,LKELM 是KELM 的一种有效的可用于数据分类的提高算法。
为了进一步对比智能算法的优化效果,本文选取SSA 优化KELM 进行对比。SSA 算法于2020 年提出,文献[14]指出其在优化方面有着良好特性。在同等样本条件下,两种智能优化算法的迭代情况如图3、图4 所示。

图3 LSO 优化KELM 分类效果

图4 SSA 优化KELM 分类效果
由图3、图4 可知,采用LSO 优化KELM 算法比SSA优化KELM 算法的收敛速度更快,其优化的精度更高。这也表明,LSO 优化KELM 算法在优化性能方面高于SSA 优 化KELM 算 法。
5 结论
本文提出的LSO 优化KELM 算法结合了KELM 与LSO 的优质特性,兼顾了全局搜索能力和局部学习能力,通过以测试准确率作为适应度函数,在迭代过程中可获得更高的分类精度。较KELM 算法,LSO 优化KELM在UCI 数据集测试获得了更高的分类效果;较SSA 优化KELM 算法,LSO 优化KELM 同样表现出更优的分类性能。

