基于双向GRU 模型的网络流量预测的研究
徐海兵,郭久明
(迈普通信技术股份有限公司 科技创新部,四川 成都 610094)
0 引言
随着网络的普及,网络流量的规模不断被刷新,高效且合理地利用网络资源变得尤为重要。一方面,网络资源分配的不合理可能导致部分网络资源由于耗尽而无法正常使用,甚至造成网络瘫痪,而其他链路资源可能却处于过剩的状态,严重影响了用户的上网体验;另一方面,虽然在前期合理分配了网络资源,但网络流量具有突发性,原本充足的网络资源可能出现短缺的情况。为了解决此问题,现有软件定义网络(Software Defined Network,SDN)[1]控制器会实时检查链路状况,在一定程度上缓解了网络拥塞,但由于调度时已经发生了拥塞,无法满足更高等级、更好服务质量的要求。鉴于此,如果能够精准预测网络流量,提前发现未来时刻的网络流量变化情况,流量调度系统则可以提前进行合理调度,有效避免拥塞的发生。
1 相关工作
1.1 基于统计的模型
基于统计的模型通常先采用差分法对网络流量原始数据平稳化处理,提取网络流量数据的自相似特征,然后将平稳后的数据通过统计模型进行拟合和检验[1],例如ARMA、ARIMA[2]等统计模型。统计模型本身十分简单,只需要内生变量而不需要借助其他外生变量,但统计模型只能捕捉线性关系,而不能捕捉非线性关系;同时要求自身或差分之后的数据是平稳的,例如无法用统计模型预测股票类型的数据,因为数据是非平稳的且受政策和新闻等其他事件影响[3]。
1.2 基于机器学习的模型
基于机器学习的流量预测模型包括梯度提升决策树[4]、回归模型[5]以及boosting 模型[6]等,首先需要对原始的数据进行分类、统计、补缺、寻找等操作,得到时间差异序列、时间趋势序列和时间序列,以此增加样本特征的多样性[6]。虽然机器学习模型对线性或非线性规律有较强的拟合能力,但需要挖掘尽可能多的样本特征,增加了模型开发的难度。
1.3 基于经验模态分解的模型
为了改善流量预测的滞后性,一些文献提出经验模态分解(Empirical Mode Decomposition,EMD)[7]和集成经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)[8]的理论方法,其方法为将访问流量数据分成若干个IMF分量和残余分量Res,之后针对IMF 分量和Res 分量分别运用统计模型、机器模型或神经网络模型进行预测,最后将各自的预测结果进行叠加重构[9]。本文针对该方法进行实验,结果表明该理论方法虽然对规律性较强的流量数据有较好的滞后性改善,但对变化幅度较大的流量数据存在IMF 分量数量不确定的问题,如果强行指定流量数据分解的IMF 数量,则存在流量预测的准确性不高的问题。
1.4 基于循环神经网络的模型
由于循环神经网络RNN 考虑了时间序列之前的信息,故非常擅长处理序列数据,已在众多领域(包括语音识别、文档识别、手写识别及图像分析)中得到广泛应用[10]。长短期记忆循环神经网络(Long Short-Term Memory,LSTM)在解决了梯度消失和爆炸问题后,能够更好地进行分类和预测任务[11]。门控循环单元GRU 是LSTM 的一种变体,保持了LSTM 效果的同时又使结构更加简单,能够很大程度提高训练的效率[12]。
2 流量预测模型
2.1 基于循环神经网络GRU 预测过程
首先对某公司的互联网出口的网络流量进行聚合形成流量时间序列,对流量时间序列的异常值采用孤立森林算法去除,对流量时间序列的缺失值采用线性插值法补齐;然后分别对最近一天的流量时间序列、最近第二天的流量时间序列、最近一周前相同时间的流量时间序列分别滑动48 个时间窗口,最终形成维度为48×3 的样本特征[[Xt-47,Xt-(47+48),Xt-(47+336)],…,[Xt-1,Xt-49,Xt-337],[Xt,Xt-48,Xt-336]],样本标签Yt的值等于Xt+1。将样本特征和样本标签形成的样本集划分为训练集和测试集,采用K 折交叉验证,在精确性方面采用均方根误差(Root Mean Square Error,RMSE)和平均百分比误差(Mean Absolute Percentage Error,MAPE)作为评估函数。

其中,n 为测试集的个数;Predictedt+1为t+1 时刻的预测值,observedt为t 时刻的真实值;自定义差异性的度量函数DIFF 用来度量t+1 时刻预测值与t 时刻真实值之间的差异性,如果测试集的波动性较强且DIFF 较小,则可能存在滞后性。需要注意的是,针对波动较小的流量曲线,则DIFF 的数值无法反映滞后性。
2.2 预测结果以及分析
测试集2020.9.29 日20:30:00 到2020.10.01 日00:00:00 之间预测值和真实值如图1 所示,横轴代表为流量发生的时刻,其上标代表星期,如212代表星期二的21:00 时;纵轴代表为流量值的大小,预测结果MAPE=27.55,MSE=238.15,DIFF=43。从准确性方面来看,预测值与真实值的趋势较为一致,但从细节中不难发现流量极值部分预测存在明显的滞后性,即流量的t+1 的预测结果和t 时刻的真实值较为一致。

图1 GRU 模型测试结果
3 改进的双向GRU 模型的流量预测方法
从上文可以看出,基于GRU 的流量预测模型虽然在准确度方面基本满足要求,但预测时存在较为严重的滞后性问题,而流量预测的滞后性无论是对智能网络的故障预测还是针对SDN 的流量调度均存在致命影响,流量预测的滞后性会导致流量预测变得毫无意义。鉴于此,流量预测的滞后性成为流量预测过程中的必须解决的一个难题。本文重点从多维特征输入、基于日期的模型分类、自定义损失函数等方面来改善流量预测的滞后性问题,同时提高流量预测的准确度。
3.1 多维特征输入
基于GRU 的流量预测模型存在滞后性问题主要是由于流量的自身规律性不明显,模型倾向性加大了上一个时间步的流量大小所对应的参数权重。通过对流量的规律性进行分析发现,流量呈现每周和每天的规律性,如图2 所示,横坐标代表的是时刻,其上标代表星期,坐标点间隔3 小时,其中周一到周五8:30~18:00 是工作时间,其他是非工作时间。
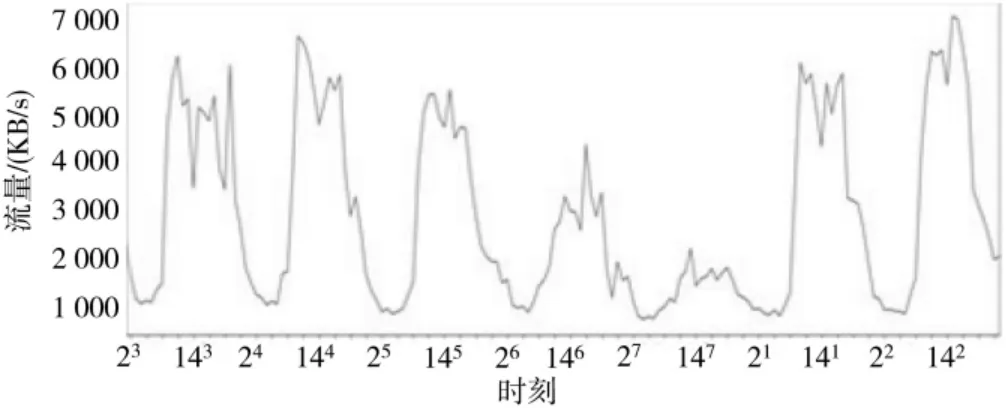
图2 流量的规律性
根据上述分析,增加流量的时间属性作为样本特征,具体为将样本标签对应的时间分解为星期、小时、分钟,同时针对流量存在突发的规律,增加流量的事件特征,根据流量的突发性大小共分为高、中、低3 种事件类型,例如是否有视频会议、是否有集体性活动等,将时间特征和事件特征进行独热编码,输入全连接神经网络[13],如图3 所示。经过多维特征的模型输入,降低上一个时间步的参数权重,从而改善流量预测的滞后性。
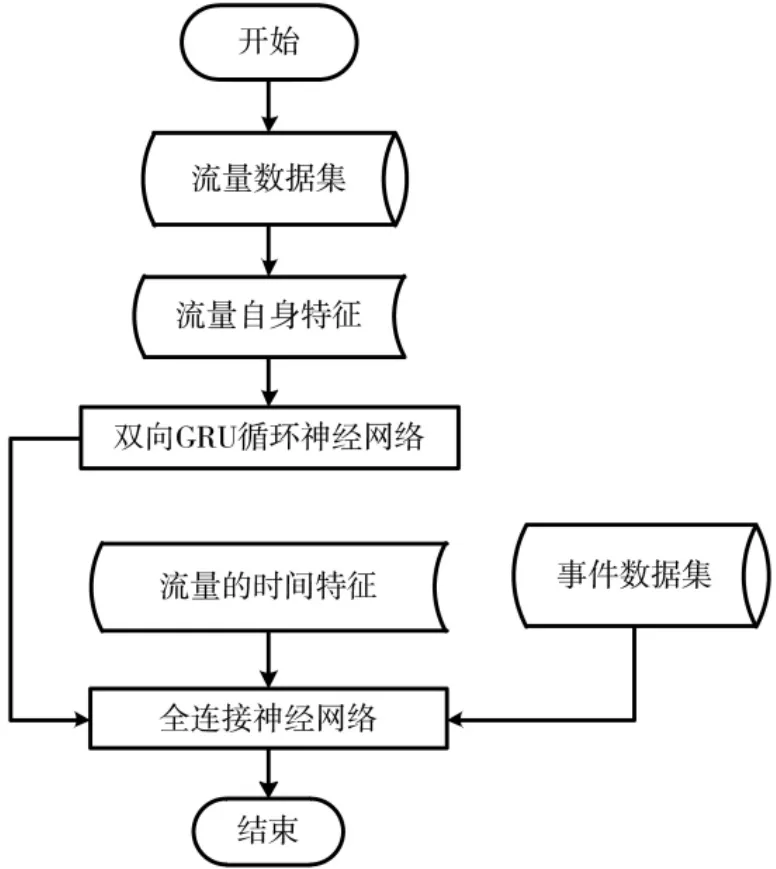
图3 多维特征流程图
将2020 年8 月29 日到2020 年9 月30 日之间的流量作为样本集,其中前几个星期的流量作为训练集,最后一个星期的流量作为测试集,将每个样本的144 维的特征向量输入到双向循环网络,将每个样本的33 维的时间特征向量以及3 维的事件特征向量输入到全连接神经网络。经过测试发现滞后性明显改善,与此同时准确性也有所提高,输出结果为MAPE=19.16,RSME=200.76,DIFF=28.59,如图4 所示。
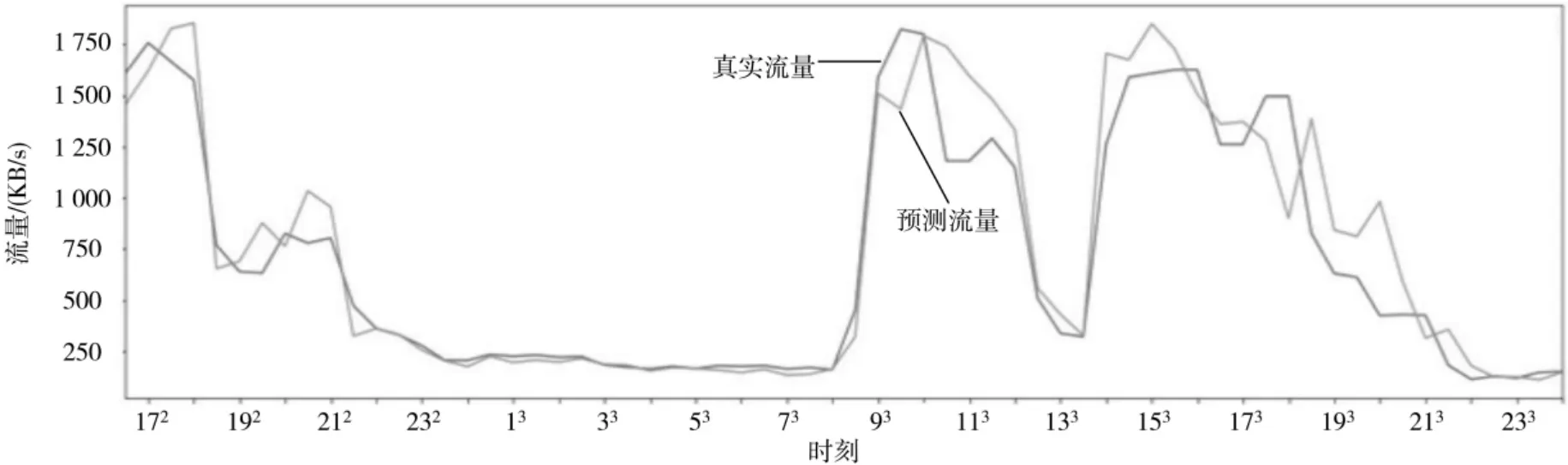
图4 多维特征测试效果图(局部)
3.2 基于日期的模型分类
考虑到非工作日的权重参数可能影响到工作日的模型参数,本文将流量数据集的时间是否为工作日进行分类,根据分类结果分别建立工作日模型和非工作日模型,如图5 所示。

图5 日期模型的流程图
工作日模型的输入是31 维的时间特征向量,非工作日模型输入是29 维的时间特征向量,法定节假日归属于非工作日类型,流量特征向量和特征向量同3.1 小节所述。测试验证的结果为MAPE=12.2,RMSE=100.63,DIFF=34.4,从图6 以及统计数据不难看出,DIFF 增大而MAPE 值和RMSE 值降低,说明整体上滞后性问题有所改善且准确性进一步提升。

图6 日期模型的测试效果图
3.3 自定义损失函数
在流量预测的过程中,尤其是在SDN 的调度场景中,对流量的峰值预测结果较为关注,预测值应稍大于实际值为最佳。然而现有的样本存在不平衡现象,即大部分样本分布在非工作时间对应的低值部分,导致峰值预测精度不高。为了解决此问题,一方面从样本不平衡的角度出发,增强极大值的样本数量,具体为通过重采样极大值范围的样本特征,然后将样本标签加入一定的白噪声,新的样本标签Ynew=Yold+Nt,其中Yold是重采样前的样本标签,Ynew是采样后的 样本 标签,Nt取[0,Yold×10%]区间内的白噪声。为了进一步加大极大值预测错误的惩罚,自定义模型的损失函数:
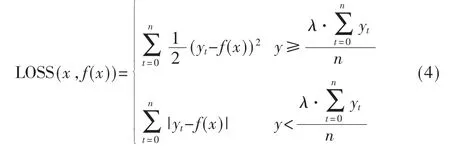
其中,yt为样本集的标签值,f(x)为模型的预测值;λ 用来调节极大值的范围,本文选择λ=1.2。使用与3.1 小节同样的数据集,采用上述的样本不平衡方法以及自定义损失函数进行模型训练和预测,测试结果为MAPE=15.93,RMSE=152.16。从图7 中不难看出,峰值预测的准确性进一步提高,但极小值部分的预测准确性有一定的下降,整体上符合预期。
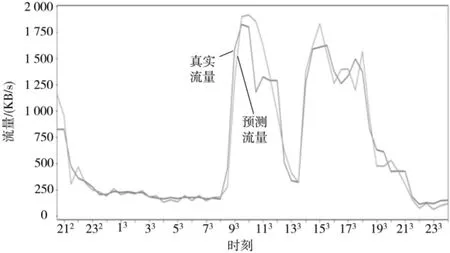
图7 自定义损失函数的测试效果图
4 结论
本文选择循环神经网络GRU 作为流量预测的理论模型,针对预测过程普遍存在的滞后性以及准确性不高的问题,提出一种改进后的双向循环神经网络GRU 模型,通过对预测过程中的结果分析,针对性采取多维特征输入、基于日期的模型分类、自定义损失函数多个步骤改进预测的结果,其中多维特征输入和基于日期的模型分类对流量预测的滞后性有明显改善,能大幅提升预测的准确性,样本再平衡以及自定义损失函数对流量峰值的预测能够达到预期的目标。后续的研究中将探索使用注意力机制[14]以及基于时间的卷积神经网络TCN[15]对流量预测的精度进一步进行提升。

