含有点蚀故障的人字行星齿轮传动系统动态分析

任 菲， 王得玺， 时桂芹， 梁 栋， 王 宁， 王 琪

(1.郑州轻工业大学 机电工程学院，河南 郑州 450002； 2.郑州轻工业大学 食品与生物工程学院，河南 郑州 450001； 3.重庆交通大学 机电与车辆工程学院，重庆 400074； 4.中铁工程装备集团有限公司，河南 郑州 450016)

0 引言

人字齿轮具有承载能力强、轴向力小和高重合度等优点，广泛应用于航空发动机、舰船汽轮机、起重机械、采煤机等重型机械传动系统中。由于高负荷、恶劣的工作环境和不可避免的疲劳破坏，齿轮很可能发生故障。早期进行故障诊断可以有效防止灾难性故障的发生。由于双齿圈人字行星传动系统的整体结构比较复杂，发生故障的几率比较高，因此对其进行故障分析具有重要的意义[1-4]。

近年来，为了探究齿轮故障的产生机理，学者们进行了大量的研究。Ma等[5]建立了具有局部剥落缺陷的直齿轮副动力学模型，研究了剥落故障对系统啮合刚度和动态响应的影响。Jiang等[6]建立了六自由度斜齿轮副解析模型，对含有齿裂缺陷的斜齿轮副动态特性进行了分析。Ren等[7-8]建立了考虑制造误差的人字行星齿轮模型，对系统动力学特性和均载特性进行了研究。徐向阳等[9]考虑齿轮安装变位特征，对含有故障的行星齿轮系统进行了动力学响应求解。陆崇山等[10]利用集中参数法，考虑了时变啮合刚度、综合啮合误差等因素，建立了两级行星传动系统平移-扭转模型，研究了系统均载特性。

随着计算机仿真软件的发展，许多科研人员使用仿真软件对齿轮传动系统进行分析。王子涵等[11]利用ANSYS，建立了行星变速箱的刚柔耦合虚拟样机模型，研究了齿轮故障对行星传动系统动态特性的影响。范志锋[12]建立了含有点蚀故障的行星轮系虚拟样机，对齿轮啮合力进行了仿真研究。余波等[13]建立了行星减速器虚拟样机模型，得到了系统动态啮合力、转速比等。刘晓乐等[14]建立了两级行星齿轮断齿故障虚拟样机模型，分析断齿故障对系统的影响。张鸿等[15]使用ADAMS分析了GTF齿轮传动系统不同条件下的振动特征及原因。张永祥等[16]建立了包含不同深度裂纹的齿轮箱虚拟样机模型，分析了裂纹深度对齿轮箱振动信号的影响。刘振皓等[17]建立了复合行星齿轮传动系统虚拟样机模型，获得了系统轮齿动态接触力变化规律。刘凯文等[18]在ADAMS中建立了某减速器多刚体和刚柔耦合模型并进行了动力学仿真，得到了系统啮合力变化特征。刘竹丽等[19]利用SolidWorks和ANSYS对斜齿轮副进行了接触和可靠性分析。

综上，许多研究主要集中在直齿轮和斜齿轮，对人字行星齿轮传动的研究较少。此外，一些研究人员建立的模型比较简单，仿真结果不准确。本文建立了含有不同点蚀故障形式的双齿圈人字行星齿轮传动系统虚拟样机模型，对不同形式系统的接触力频谱特征和均载性能进行了分析。

1 系统基本结构

1.1 基本参数

图1为行星齿轮传动系统简图。该系统主要由1个太阳轮、5个行星轮、2个螺旋角相反其他参数均相同的内齿圈和1个行星架组成，齿轮均为人字齿轮，内齿圈固定，动力由太阳轮输入，行星架输出，基本参数如表1所示。

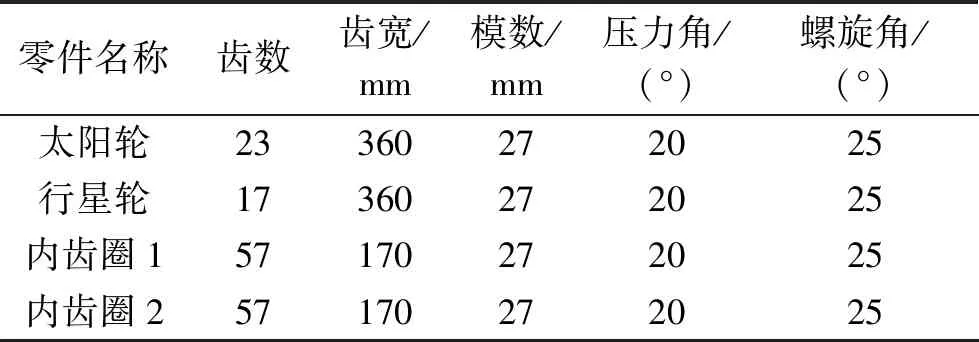
表1 行星齿轮参数表Table 1 Planetary gear parameter table

图1 行星齿轮传动系统简图Figure 1 Schematic diagram of planetary gear transmission system

1.2 理论参数

齿圈固定时，行星齿轮传动系统传动比计算式为

(1)

式中：zs和zr分别为太阳轮和齿圈的齿数。

齿轮转动频率计算式为

f=n/60。

(2)

式中：n为各构件转速，r/min。

人字行星齿轮传动啮合频率的计算式为

(3)

式中：ωs为太阳轮的角速度，(°)/s。

通过计算得到系统的传动比为3.478，太阳轮转动频率fs=1.67 Hz，行星轮转动频率fp=1.12 Hz，行星架转动频率fc=0.47 Hz，啮合频率fm=27.37 Hz。

2 虚拟样机模型的建立

2.1 模型的建立

使用KISSsoft和SolidWorks建立无故障系统三维模型，经过虚拟装配后通过干涉检查，确保系统不存在干涉[12]。保存为x_t格式导入到ADAMS中，生成的虚拟样机模型如图2所示。

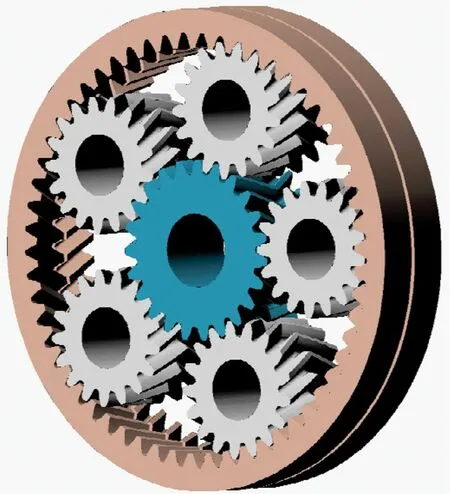
图2 双齿圈人字齿行星传动虚拟样机Figure 2 Virtual prototype of double ring herringbone planetary transmission

2.2 点蚀故障的模拟

模拟太阳轮发生点蚀故障，建立2种不同形状的点蚀故障，形状为矩形[9]和圆形[12]，点蚀深度为2 mm，如图3所示。在圆形点蚀的基础上，建立3种不同数量的点蚀故障，数量取2～6个，点蚀深度为2 mm，以及3种不同深度的点蚀故障模型，点蚀深度取1～3 mm。单侧矩形点蚀和圆形点蚀的面积约为700 mm2。使用存在点蚀故障的太阳轮替换无故障太阳轮，生成不同类型的点蚀故障虚拟样机模型。

图3 太阳轮点蚀故障类型Figure 3 Types of sun gear pitting failure

2.3 约束的施加

对虚拟样机模型各构件添加相应的运动副，运动副包括：太阳轮、行星轮和行星架的旋转副、内齿圈的固定副[15]。对太阳轮添加转速ns=100 r/min，对行星架添加负载Tc=100 kN·m，转速和负载用step阶跃函数表示[14]。

2.4 接触的设置

在ADAMS中进行动力学求解时，需对各齿轮副进行接触设置，可由CONTACT接触函数实现，该函数以Hertz弹性接触理论为基础，以啮合节点为计算位置[17]。刚度系数计算式为

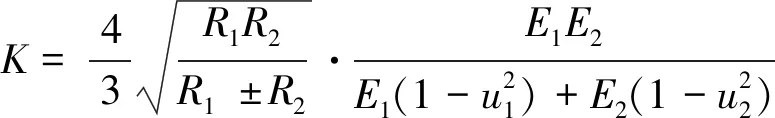
(4)

式中：R1、R2为齿轮副的啮合半径，一般取分度圆半径；E1、E2为齿轮材料弹性模量；u1、u2为泊松比。

齿轮材料为20CrMnMo，弹性模量E=2.06×109Pa，泊松比u1=u2=0.29，计算得到外啮合接触刚度K1=3.17×108N/m，内啮合接触刚度K2=3.65×108N/m。穿透深度取0.1 mm，阻尼系数取刚度大小的0.1%～1%，非线性指数e取1.5，静摩擦系数取0.3，动摩擦系数取0.1。

3 无故障系统仿真

3.1 角速度分析

设置仿真时间为5 s，仿真步数为2 500。采用 GSTIFF积分法对系统进行求解，得到了如图4所示的行星齿轮传动系统输入输出角速度变化曲线。可知太阳轮输入角速度为600(°)/s，行星轮的传递角速度为401.65(°)/s，行星架的输出角速度为170.68(°)/s。齿侧间隙的存在使得行星轮啮合时产生冲击，导致其输出曲线存在一定的波动。角速度仿真可用于模型的验证，已有文献将这种方法用于实际研究中[17]。由传动比计算得到行星架输出角速度为172.5 (°)/s，与仿真结果相差1%，验证了所建模型的正确性。

图4 系统输入输出角速度曲线Figure 4 Input and output angular velocity curve of systems

3.2 接触力分析

图5为无故障内外啮合副时域和频域曲线，表2为各齿轮副的接触力。从齿轮接触力时域曲线可以看出，接触力分布均匀，未出现明显冲击。内外啮合副时域曲线均呈周期性变化，系统在0.1 s时达到稳定状态。

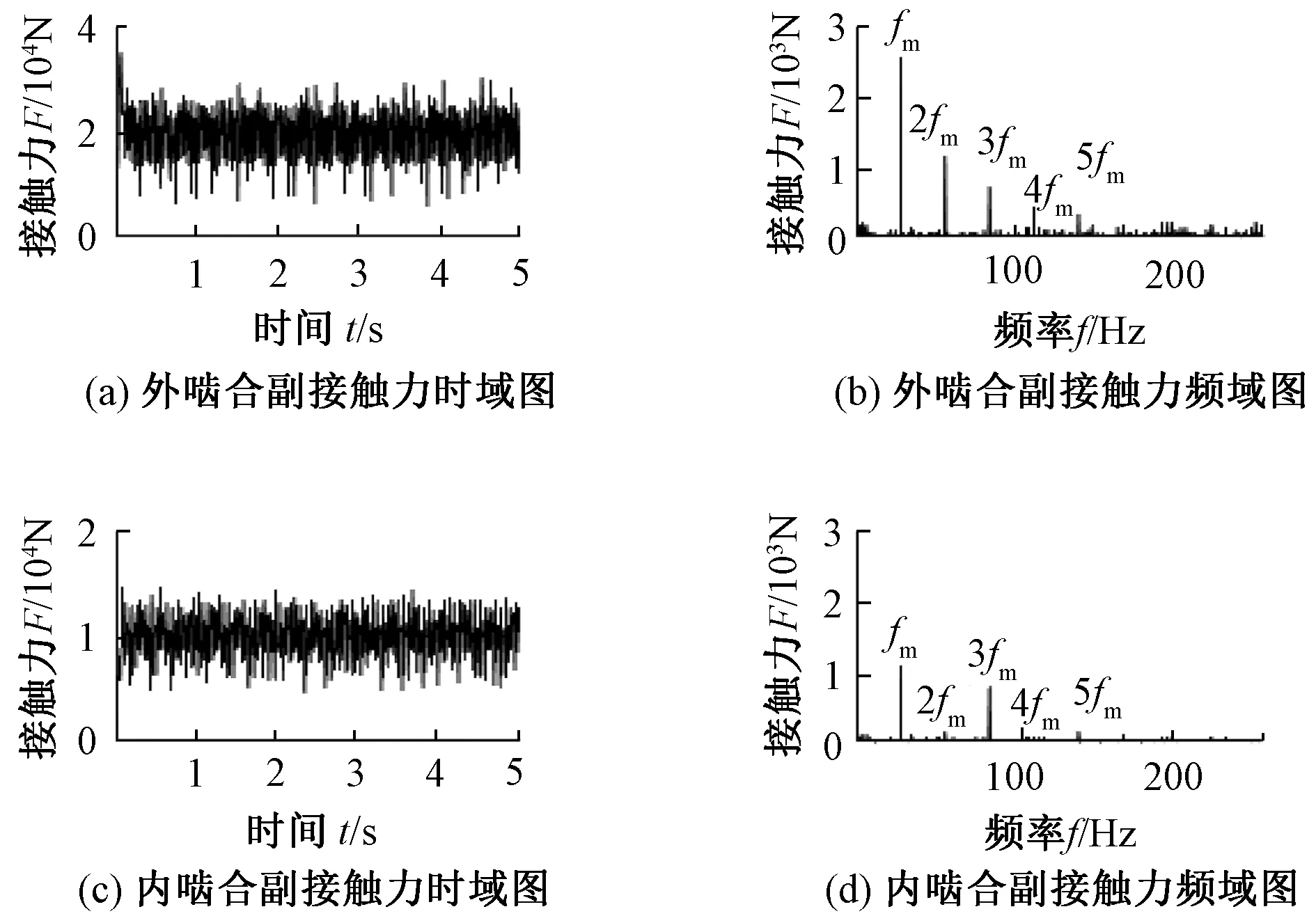
图5 无故障系统内外啮合副接触力时域和频域图Figure 5 Time-domain and frequency-domain diagram of the meshing contact force of the internal and external meshing pairs of a faultless system

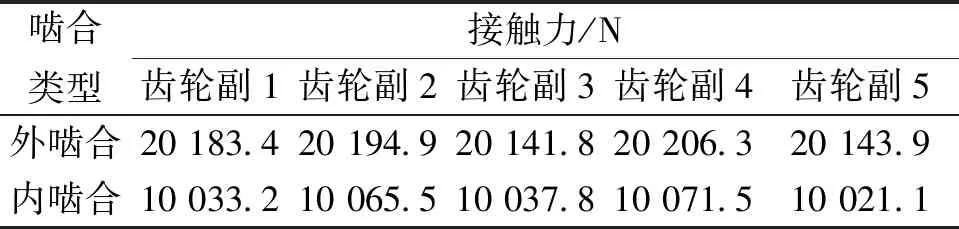
表2 无故障接触力Table 2 Contact force without failure

在频域图中，基频fm=27.34 Hz，对应系统啮合频率，误差仅为0.1%，在以往的研究中，误差不超过2%的即可认为模型是正确的[20]。本文仿真得到的基频和理论啮合频率的误差未超过2%，再次证明了模型的准确性和合理性。在外啮合频域图中，均出现了以基频为主频率2倍以上的谐波频率，各频率对应的接触力幅值差异很大。随着系统的运行，频率对应的幅值相对降低。在内外啮合频域图中，低频区域均存在与行星架、太阳轮和行星轮的转动频率相对应的频率。内啮合频域图中，基频fm和谐波频率3fm相对明显， 谐波频率2fm和4fm所对应的幅值较小。外啮合基频fm所对应的接触力约为内啮合基频所对应幅值的2倍。内外啮合的基频和谐波频率两侧均存在密集的边频带，外啮合基频和谐波频率两侧的边频带对应的幅值比内啮合大，且更加密集。

3.3 均载系数

由于齿轮弹性变形和制造误差的影响，行星齿轮承受的载荷是不等的[1]。均载系数常用来表示系统的负荷分布，均载系数越大，不同行星齿轮间的载荷分配越不平衡[8]。太阳轮-行星轮副和行星轮-内齿圈副的均载系数用λw、λn表示为

(5)

式中：N为行星轮个数；Fspi、Frpi分别代表太阳轮-行星轮副和行星轮-内齿圈副的接触力。

计算得到无故障系统内外啮合副的均载系数分别为1.002和1.003，理想的均载系数为1，均载系数越小，系统均载性能越好。

4 点蚀故障系统仿真

4.1 不同形状的点蚀故障

通过仿真，得到了图6和图7所示的太阳轮存在2种不同形状点蚀时内外啮合副接触力时域和频域曲线。由图6、7可以看出，圆形点蚀的峰值特征要比矩形点蚀明显，且呈周期性出现。图6中的内外啮合时域图中分别标出了5个接触力峰值，其中圆形点蚀外啮合频域图中的5个峰值所对应的时间分别为0.88、1.72、2.56、3.48、4.248 s，时间间隔约为0.84 s。圆形点蚀内啮合5个峰值所对应的时间分别为0.704、1.552、2.400、3.232、4.072 s，周期同样为0.84 s，矩形点蚀时域图中也具有这种周期性，其中外啮合峰值周期约为0.95 s，在矩形点蚀内啮合时域图中，这种周期性表现不太明显。表明矩形点蚀对系统内啮合的影响较小。存在点蚀故障时，基频和谐波频率与无故障系统的特征一致，基频所对应的幅值有所降低。所有内啮合的频域中，2fm处所对应的接触力幅值发生了突变，幅值比无故障系统要大。基频和谐波频率两侧的边频带更加密集，其中圆形点蚀造成的冲击较大，接触力频域曲线中基频两侧的边频带比矩形点蚀的还要密集，表明圆形点蚀对系统整体性能影响比矩形点蚀大。

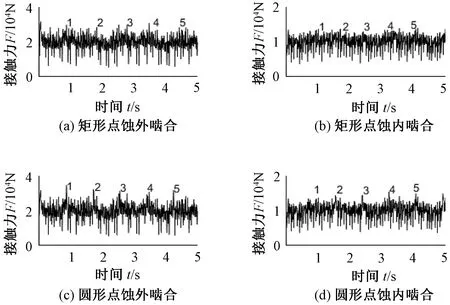
图6 不同形状点蚀故障内外啮合副时域图Figure 6 Time domain diagram of internal and external meshing of pitting faults with different shapes

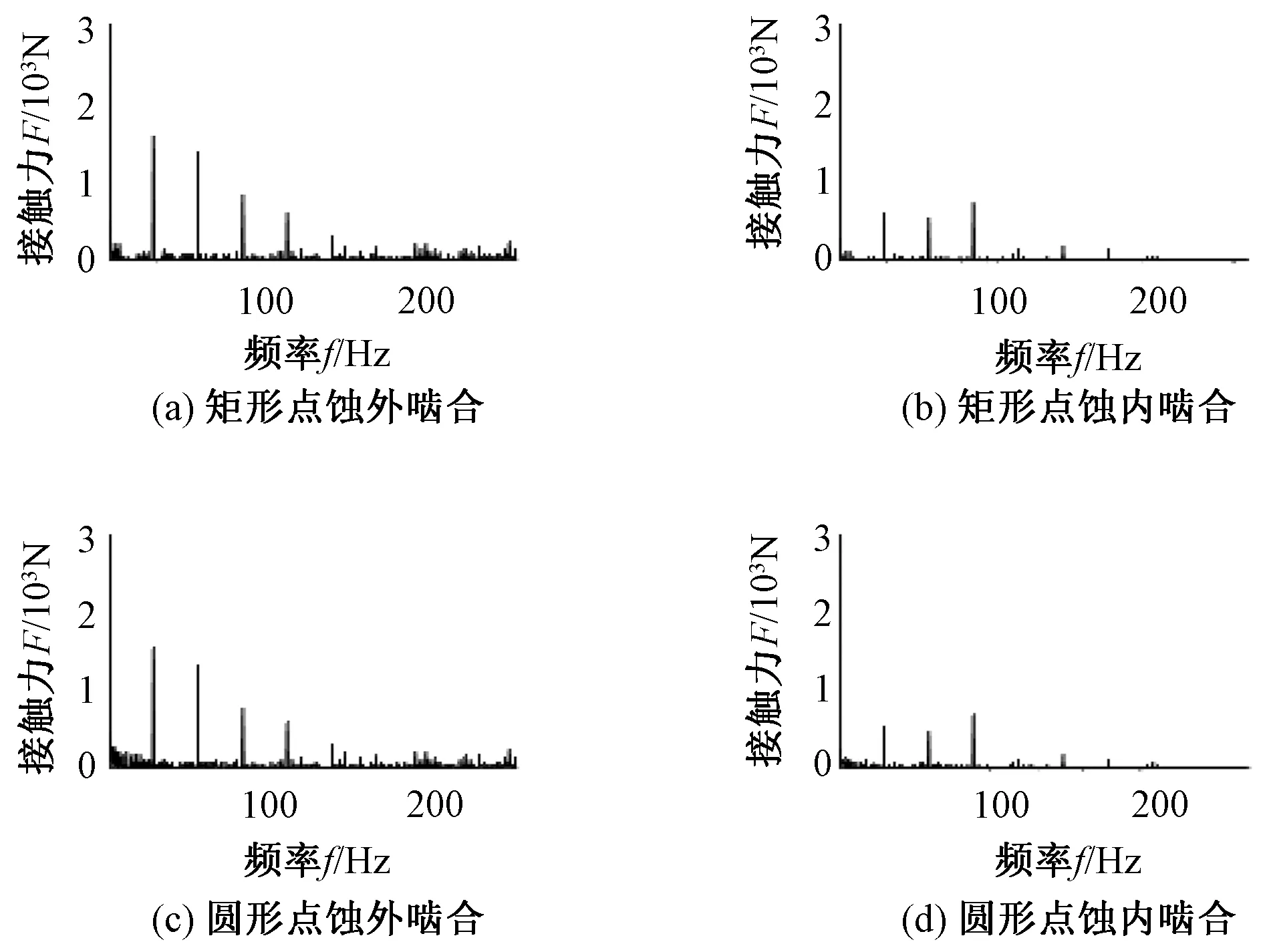
图7 不同形状点蚀故障内外啮合副频域图Figure 7 Frequency domain diagram of internal and external meshing of pitting faults with different shapes

表3为太阳轮存在矩形点蚀和圆形点蚀时系统的内外啮合副接触力。由表3可以看出，发生点蚀故障时，外啮合副的接触力整体有所降低，内啮合接触力有所增加，接触力幅值变化在200 N以内。计算出太阳轮存在圆形和矩形点蚀时外啮合副的均载系数分别为1.006 5和1.006 4，内啮合的均载系数分别为1.009 7和1.009 5，存在圆形点蚀时计算得到的均载系数比矩形点蚀大，表明圆形点蚀对系统均载特性的影响比矩形点蚀大。

表3 不同点蚀形状齿轮副接触力Table 3 Contact force of gear pairs with different pitting shapes

4.2 不同数量的点蚀故障

对太阳轮存在不同点蚀数量的系统进行仿真，发现矩形点蚀和圆形点蚀得到的结果相近。随着点蚀数量的增加，接触力变化规律基本一致。所以仅给出了太阳轮存在4个圆形点蚀时的内外啮合副接触力时域和频域曲线图，如图8所示。

太阳轮存在2个圆形点蚀时的时频变化曲线与图6和图7中的圆形点蚀一致。由图8可以看出，点蚀数量为4时，接触力时域中的峰值接触力更加突出，具有规律性。图8中的峰值接触力幅值要比图6中的峰值接触力要大。随着点蚀数量的增加，这种现象也越来越明显。故障轮齿和无故障轮齿啮合一次，就会产生一个接触力峰值。

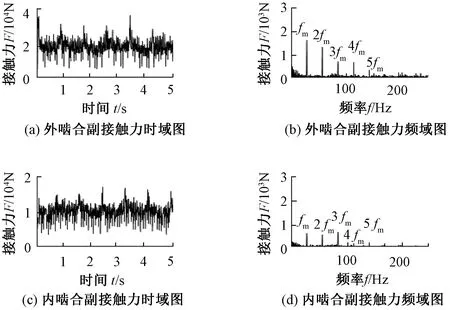
图8 圆形点蚀(4个)内外啮合副接触力时域和频域图Figure 8 Contact force time-domain and frequency-domain diagram of circular pitting (4) internal and external meshing pairs

由频域图看出，外啮合的频域变化规律与健康系统一致，但基频发生了变化。发生点蚀故障时，外啮合频域图中的基频fm=28.44 Hz，相对于健康系统基频增加了4%，对应的接触力幅值为1 599 N，降低了约1 000 N。2fm和4fm所对应的接触力幅值增加，3fm所对应的幅值有所下降。无故障系统内啮合频域图中，2fm所对应的接触力为144.7 N，发生点蚀故障后，对应的幅值增加了4倍。2fm和3fm对应的幅值均增加，基频和4fm对应的幅值均有所下降，基频和谐波频率两侧的边频带比图7中的还要密集，点蚀数量越多，这种特征越显著。

表4为太阳轮存在不同数量的圆形点蚀时各齿轮副接触力，可知太阳轮存在4个圆形点蚀和6个圆形点蚀时系统的外啮合均载系数分别为1.008和1.009，内啮合均载系数分别为1.011和1.012，随着点蚀数量的增加，均载系数呈增大的趋势，表明点蚀数量的增加会造成系统均载性能变差。

4.3 不同深度的点蚀故障

以太阳轮存在2个圆形点蚀为例，取点蚀深度为1～3 mm。经过仿真得到了太阳轮存在不同点蚀深度的接触力时频曲线，2 mm点蚀深度的仿真结果与图6(c)、6(d)、7(c)、7(d)相同，3种点蚀深度仿真得到的接触力时频曲线变化规律一致，所以本节只给出了图9所示的点蚀深度为3 mm时的系统接触力时频曲线。从时域曲线可以看出，图中同样出现了周期性接触力峰值，随着点蚀深度的增加，时域曲线中的接触力峰值变大。从频域图来看，存在不同点蚀深度故障的系统各齿轮副所对应的基频与无故障时的基频相同，均为27.34 Hz。与无故障系统频域曲线相对比，外啮合频域图中的基频fm所对应的幅值降低了约40%，2fm、3fm、4fm对应的幅值均有所增加，分别增加了约12%、10%、47%。内啮合频域图中的基频fm和谐波频率3fm所对应的幅值分别降低了约48%、10%，2fm所对应的幅值增加了约3倍，4fm对应的幅值增加了约1倍。随着点蚀深度的加深，基频和谐波频率两侧边频带更加密集。

表4 不同点蚀数量齿轮副接触力Table 4 Contact force of gear pairs with different pitting numbers

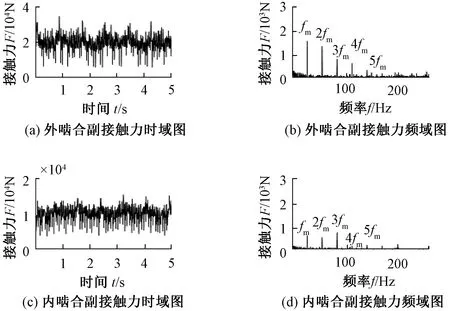
图9 圆形点蚀(3 mm)内外啮合副接触力时域和频域图Figure 9 Time-domain and frequency-domain diagram of the contact force of the internal and external meshing pairs of a circular pitting(3 mm)

表5为太阳轮存在不同深度的圆形点蚀时仿真得到的接触力，计算得到圆形点蚀故障深度为1 mm时的内外啮合副均载系数分别为1.010和1.006，点蚀深度为3 mm时的内外啮合副均载系数分别为1.011和1.007。综合太阳轮存在矩形点蚀故障且深度为1～3 mm时仿真得到的接触力，给出如图10所示的均载系数变化曲线，无论点蚀故障是什么形状，随着点蚀深度不断地增加，系统中的均载系数越来越大，表明点蚀深度的增加会使系统均载性能变差。

表5 不同点蚀深度齿轮副接触力Table 5 Contact forces of gear pairs with different pitting depths

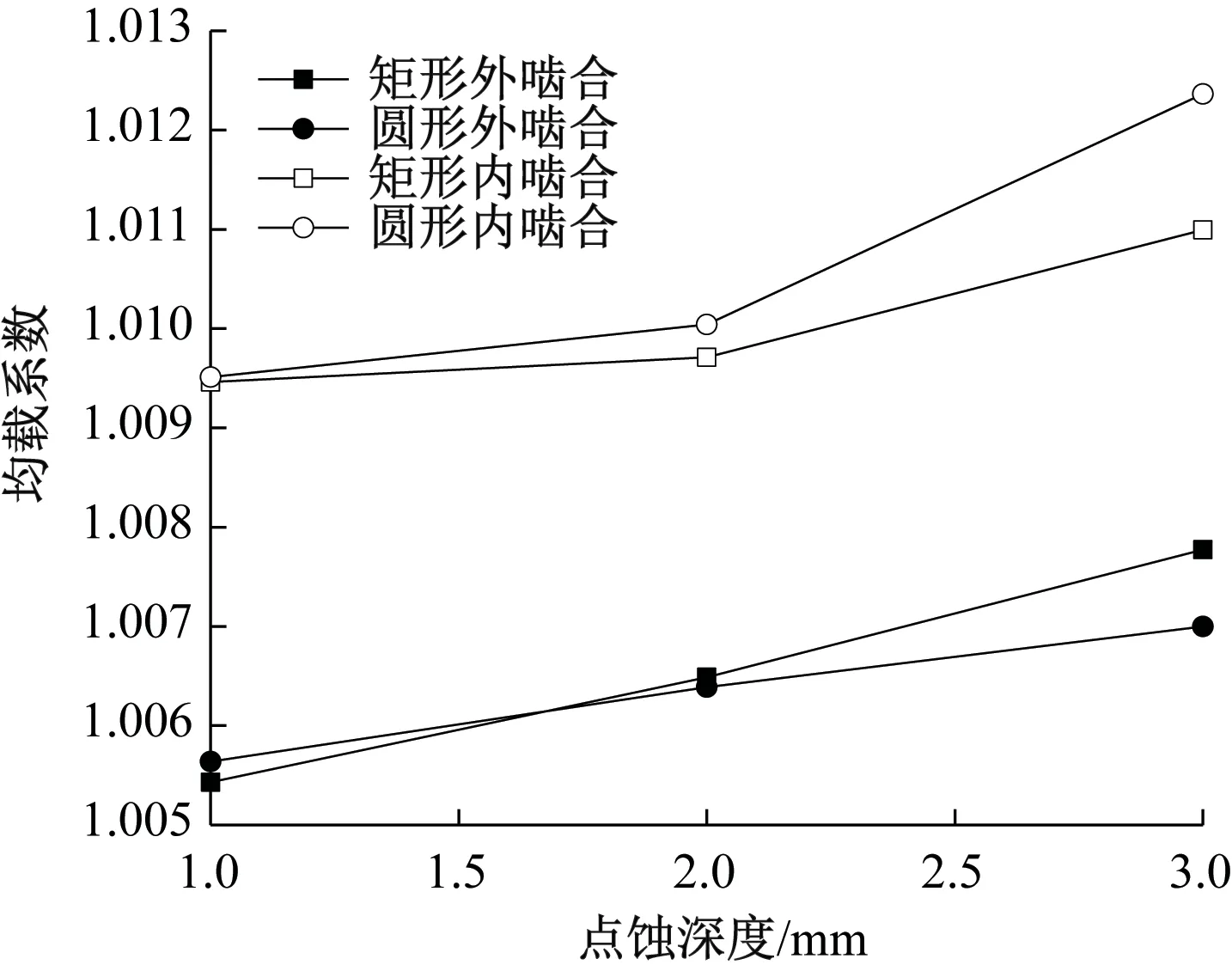
图10 均载系数变化曲线Figure 10 Variation curve of uniform load factor

5 结论

(1) 无故障系统各齿轮副接触力时域曲线呈周期性变化，接触力分布均匀，未出现明显的冲击现象。基频与系统理论啮合频率一致，频域内存在谐波频率。输出角速度仿真结果与理论值相比误差很小，仿真模型准确性较高。

(2) 存在点蚀故障时，各齿轮副的接触力时域图中出现了周期性峰值，系统出现了明显的冲击，随着故障程度的增加，冲击越来越大。

(3) 点蚀形状和深度对接触力的基频几乎没有影响，点蚀数量对基频的影响很大，太阳轮存在4个圆形点蚀时，基频增加了4%。随着点蚀数量的增加，基频对应的幅值降低，内啮合故障频域中的2fm对应的幅值明显增大。

(4) 圆形点蚀对系统均载特性的影响比矩形点蚀大，点蚀数量和深度的增加使系统均载系数变大，频域中各频率两侧的边频带变得密集。点蚀数量的增加对系统动态性能的影响大于点蚀深度的增加对系统动态性能的影响。