考虑粘结应力传递的抗弯加固锈蚀RC梁挠度计算方法
唐皇 彭建新 王晗 张建仁




摘 要:基于微元法思想,考虑锈蚀钢筋与混凝土之间粘结应力的传递,以及粘结应力传递前后截面应变的相容性,建立了钢板和FRP抗弯加固锈蚀RC梁挠度计算模型。为了验证计算模型的正确性,对比分析了多组试验结果。结果表明:在不同荷载等级下,与不考虑粘结应力的传递模型相比,考虑粘结应力的传递模型对钢板抗弯加固锈蚀RC梁的挠度计算结果更接近试验值。考虑粘结应力传递模型的极限荷载和对应极限挠度的误差范围为-0.6%~1.8%和-10.5%~9.1%,不考虑粘结应力传递模型的极限荷载和对应极限挠度的误差范围为1.1%~6.1%和-11.4%~-2.2%。该模型也能较精确地预测FRP材料(包括CFRP和BFRP)抗弯加固锈蚀RC梁的荷载挠度曲线,极限荷载值的误差范围为-3.6%~4.2%,极限挠度误差范围为-4.2%~8.3%。
关键词:钢筋混凝土梁;锈蚀;抗弯加固;挠度;粘结应力传递
中图分类号:TU375.1 文献标志码:A 文章编号:2096-6717(2022)01-0094-11
收稿日期:2020-07-11
基金项目:国家重点基础研究发展计划(973项目)(2015CB057705);国家自然科学基金(52078056);湖南省自然科学青年基金(2019JJ50023);湖南省自然科学基金(2018JJ2438);湖南省教育厅科学研究项目(18A136);2020年益阳市银城科技人才托举工程项目
作者简介:唐皇(1988- ),男,博士,主要从事桥梁结构耐久性研究,E-mail:tanghuang_123@163.com。
彭建新(通信作者),男,博士,教授,E-mail:jianxinpeng@csust.edu.cn。
Abstract: Based on the differential element method, considering transfer of bond stress between corroded steel bar and concrete, and the compatibility of cross-section strain before and after bond stress transfer is considered, the deflection calculation model of corroded RC beams strengthened by steel plates and FRP is proposed in this paper. To validate it, the testing results in existing literatures and this study, are compared and analyzed. The results show that under different loading levels, compared with the strengthened beam without considering bond stress transfer, the deflection calculation results via proposed model considered the bond stress transfer of corroded RC beam strengthened by bending is more closer to the testing values. The relative errors of the former ultimate loading and the corresponding ultimate deflection is -0.6%~1.8% and -10.5%~9.1%, respectively, while the relative errors of the latter ultimate loading and the corresponding ultimate deflection is 1.1%~6.1% and -11.4%~-2.2%, respectively. The proposed model can also accurately predict the load-deflection curve of corroded RC beams strengthened by FRP materials (including CFRP and BFRP). The improved relative error of ultimate loading value is -3.6%~4.2%, and the that for ultimate deflection is -4.2%~8.3%.
Keywords:reinforced concrete beam; corrosion; flexural strengthening; deflection; bond stress transfer
鋼筋锈蚀引起的钢筋与混凝土粘结力退化是导致钢筋混凝土(RC)结构承载性能降低的主要因素之一。利用钢板和FRP加固锈蚀RC结构是两种运用广泛且有效的加固方法。由于钢板具有加固操作方便、成本低、对结构本身破坏小等优点,已广泛运用于加固工程中。学者们对于未锈蚀加固结构承载性能和变形性能等方面的研究取得了诸多成果[1-3],但对于钢板加固锈蚀RC梁力学性能的研究较少。近年来,笔者通过对30片不同锈蚀程度的RC梁进行不同方式的钢板加固,通过试验研究得到了钢板抗弯加固锈蚀RC梁抗力退化、变形性能和破坏特征[4-5],分析了二次锈蚀对于钢板加固锈蚀RC梁后的承载性能的后续影响[6],建立了计算钢板加固锈蚀RC梁的短期挠度计算方法[7],此方法并没有考虑不同锈蚀状态下粘结应力的有效传递,而把粘结力作为定值,最终极限荷载对应的挠度值比较合理,但不同荷载等级下的挠度值与试验值略有差异。
FRP作为比较新型的加固材料,由于其刚度高、纵向拉伸强度大、抗腐蚀性好、热传递率低等优点,已经广泛运用于钢筋混凝土结构的加固工程中。粘贴FRP布加固RC结构是使用FRP材料增强RC结构性能的方法之一。学者们对FRP布加固锈蚀后的RC结构力学性能进行了一系列研究。Al-Saidy等[8-9]通过试验研究了不同锈蚀率下粘贴CFRP布加固RC梁的短期挠度、破坏模式和承载力等力学性能。Triantafyllou等[10]通过实验对比分析了轻度锈蚀、中度锈蚀和严重锈蚀对于粘贴CFRP加固RC梁的挠度、FRP应变和承载力等性能指标的影响。王晓刚等[11]研究了弱界面对CFRP剥离的影响及传统U型箍约束的有效性。以上学者主要是通过试验研究FRP加固锈蚀RC梁的力学性能,没有具体分析从理论上计算不同粘贴方式下FRP加固锈蚀RC梁的变形和承载力的方法。
笔者结合现有钢板和FRP加固锈蚀RC梁的试验和理论成果,考虑不同锈蚀情况下锈蚀钢筋和混凝土粘结滑移导致的粘结应力传递以及传递前后梁截面应变相容性,利用微元法思想,建立不同破坏模式下钢板和FRP抗弯加固锈蚀RC梁的理论分析模型,并利用笔者和其他学者的试验研究结果验证理论模型的正确性。
1 抗弯加固锈蚀RC梁变形计算模型
1.1 锈蚀钢筋与混凝土粘结滑移模型
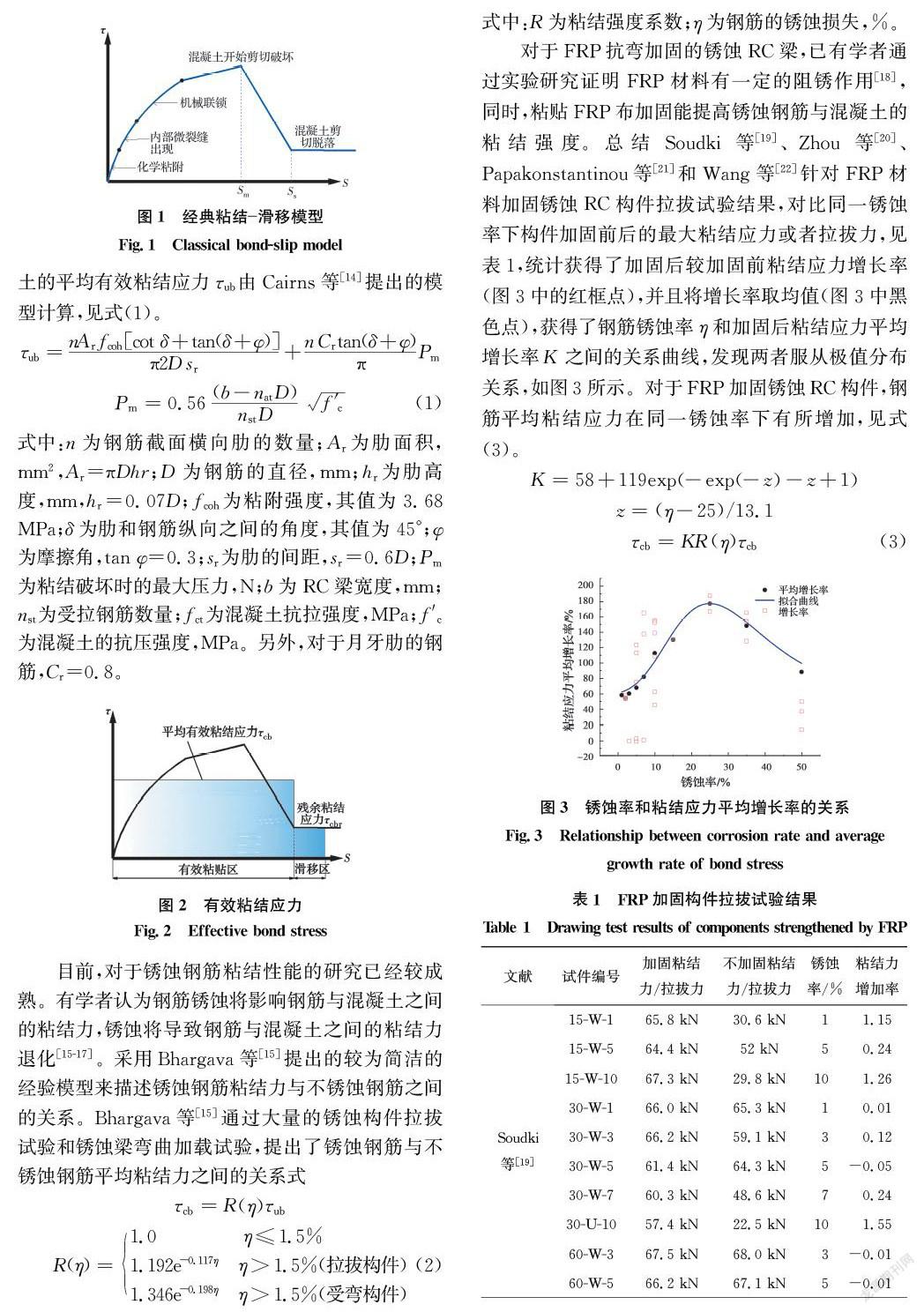
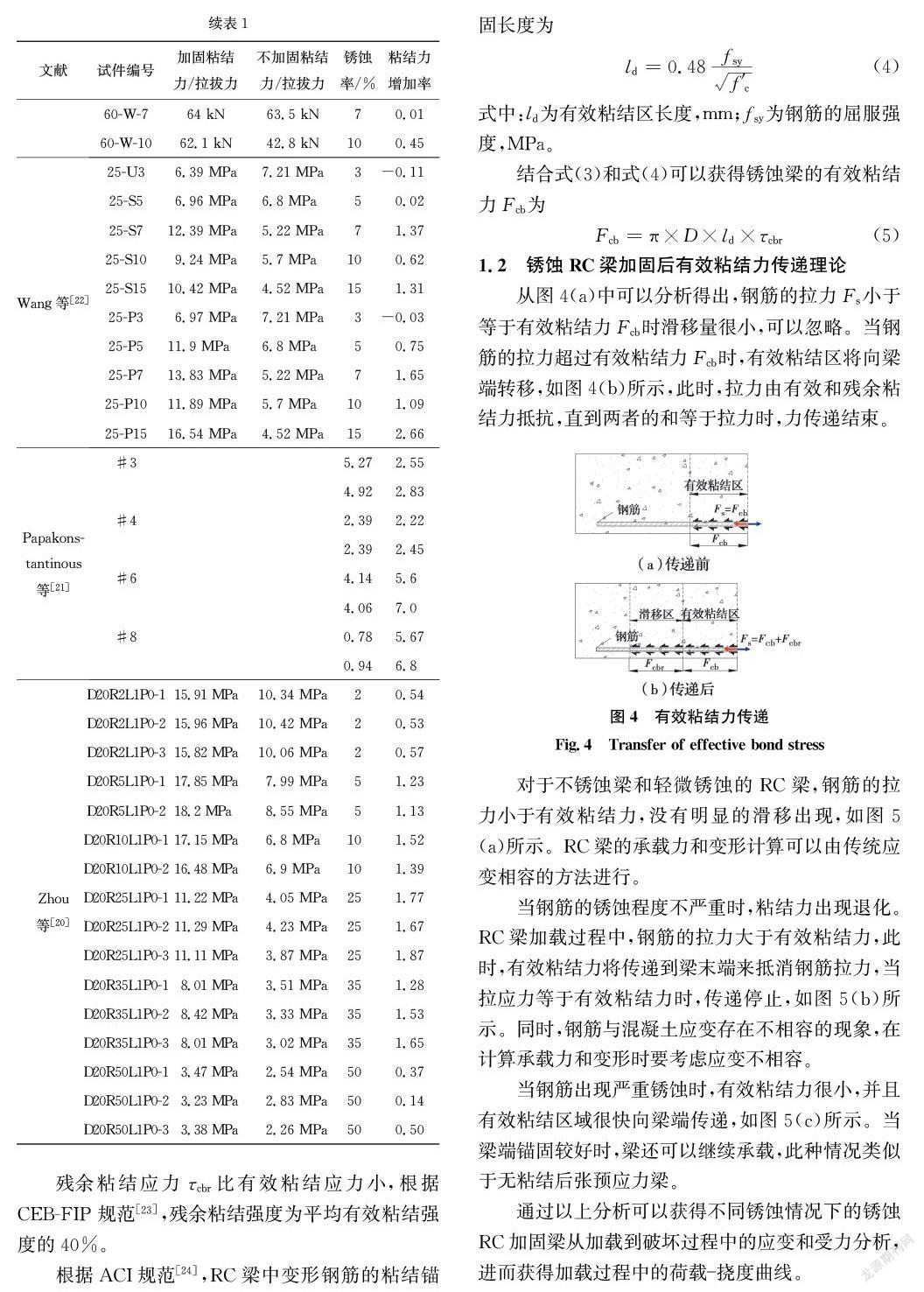
学者们对于未锈蚀钢筋与混凝土的粘结性能的研究已经较为成熟[12-13]。对于变形钢筋,采用Haskett等[12]提出的经典粘结滑移模型,如图1所示。当滑移很小时,粘结力随着滑移增加而增加。粘结力起初是因为混凝土与钢筋之间的化学粘附形成的,当混凝土内部微裂缝出现时,化学粘附消失,随着滑移继续增加,此时粘结力主要由混凝土与钢筋之间的机械联锁产生。当滑移持续增大导致混凝土开始剪切破坏时,粘结力最大,之后粘结力迅速减小,直至混凝土剪切脱落,此时粘结力称为残余粘结力,并保持不变,由混凝土与混凝土摩擦产生。图1中,从滑移开始到混凝土剪切脱落前的粘结力称为有效粘结力。
对于不锈蚀梁和轻微锈蚀的RC梁,钢筋的拉力小于有效粘结力,没有明显的滑移出现,如图5(a)所示。RC梁的承载力和变形计算可以由传统应变相容的方法进行。
当钢筋的锈蚀程度不严重时,粘结力出现退化。RC梁加载过程中,钢筋的拉力大于有效粘结力,此时,有效粘结力将传递到梁末端来抵消钢筋拉力,当拉应力等于有效粘结力时,传递停止,如图5(b)所示。同時,钢筋与混凝土应变存在不相容的现象,在计算承载力和变形时要考虑应变不相容。
当钢筋出现严重锈蚀时,有效粘结力很小,并且有效粘结区域很快向梁端传递,如图5(c)所示。当梁端锚固较好时,梁还可以继续承载,此种情况类似于无粘结后张预应力梁。
通过以上分析可以获得不同锈蚀情况下的锈蚀RC加固梁从加载到破坏过程中的应变和受力分析,进而获得加载过程中的荷载挠度曲线。
从表2可以看出,绝大多数试验梁理论破坏模式与试验破坏模式相同,钢板加固不锈蚀梁S0C25-1的破坏模式却有差异,其极限挠度试验值与理论值较其他试验梁差别大,是由于试验梁的制作加工问题,试验出现了提前斜拉破坏的情况,导致挠度偏低。
从图10中也可以看出,理论计算值比张建仁模型计算值整体上更加接近试验值。张建仁等在试验中发现,钢板抗弯加固梁破坏时,锚钉与混凝土以及钢板之间没有出现滑移,因此,试验加固锈蚀梁的破坏多为钢板和受拉钢筋之间的混凝土拉裂破坏,与本文的加固梁假设相似。同时,锚钉位于保护层内,对钢筋与混凝土之间的粘结影响较小。张建仁等[7]的计算结果中,在同一荷载作用下挠度值比试验值偏小,其原因可能是模型中虽然划分了若干单元,但纵向钢筋粘结力沿梁长每个单元为相同的定值,没有考虑粘结力的传递,因此,与该模型相比,缺少粘结应力传递后的应变不相容分析,所有微梁段的应变分布相同。对比极限承载力和对应的挠度大小,理论模型与试验值的误差分别是-0.6%~1.8%、-10.5%~9.1%,张建仁模型理论值与试验值的误差分别是1.1%~6.1%、-11.4%~-2.2%。
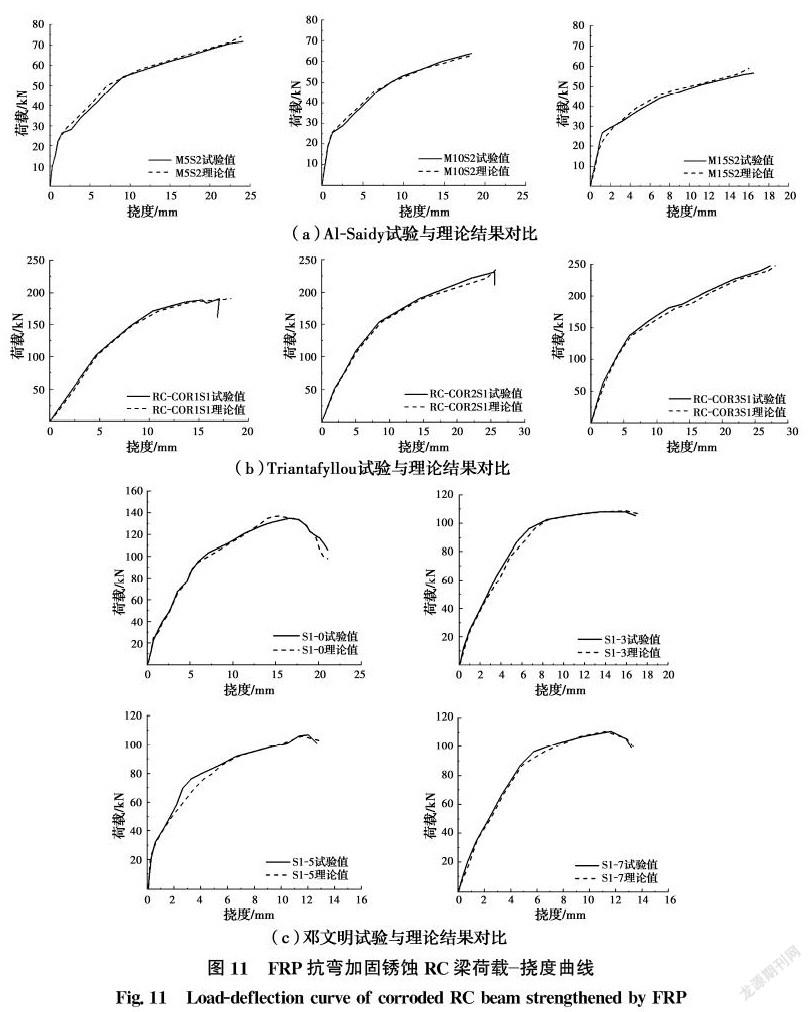
从图11中可以看出,无论是CFRP(Al-Saidy等[8]、Triantafyllou等[10])和BFRP(邓文明[28])加固锈蚀RC梁,模型能较好地预测其荷载挠度曲线。从表1中可以看出,极限荷载值的误差为-3.6%~4.2%,极限挠度误差为-4.2%~8.3%。
图10(a)和11(c)中还列出了钢板和BFRP加固不锈蚀梁的荷载挠度曲线,其理论计算结果也可由该模型获得,程序只需计算阶段1和阶段2,结合式(18)和式(19)便可获得理论的荷载挠度曲线。从图10(a)和图11(c)中可以看出,不锈蚀加固试件S0C25-3 和S1-0的理论荷载挠度曲线与试验曲线都比较吻合。由表2中可以看出,钢板和BFRP加固不锈蚀RC梁极限荷载和对应的挠度误差分别是:2.8%、13.9%、1.6%、8.4%。
从Bhargava等[15]的粘结力模型中可以看出,当钢筋锈蚀率大于1.5%时,构件粘结力就开始退化,但Zhang等[29]指出,当钢筋的锈蚀率低于7%时,钢筋与混凝土应变不相容现象不明显,因此,对于锈蚀率低于7%时的试验梁将不考虑粘结力传递,循环计算只考虑阶段1和2。图10和图11所选取的试验梁中,梁M5S2锈蚀率为5%,其他梁均大于7%。从图11(b)中可以看出,梁M5S2的挠度在同一荷载下略大于理论值,这可能是因为其钢筋发生了轻微的粘结滑移,粘结力传递发生了,但传递长度很小,导致同一荷载下的挠度稍微变大,但是增大的幅度很小,基本可以忽略不计。因此,从上述分析中可以看出,该理论模型也能较精确地预测不考虑粘结力传递的试验梁(不锈蚀梁和微锈蚀梁)荷载挠度曲线。
3 结论
考虑不同锈蚀情况下锈蚀钢筋和混凝土的粘结滑移导致的粘结应力滑移,利用微元法思想,建立不同破坏模式下钢板和FRP抗弯加固锈蚀RC梁的理论分析模型,并且利用现有试验结果对比分析了该模型的精确度,获得了以下结论:
1)計算模型考虑了不同锈蚀状态下粘结应力传递,同时进行了应力传递前后应变相容性和不相容性分析,与现有模型相比,能更准确地模拟了抗弯加固锈蚀RC梁荷载作用下的变形过程,同时也可以较精确地预测不锈蚀加固梁和微锈蚀加固梁的荷载挠度曲线。
2)对于钢板抗弯加固锈蚀RC梁的挠度计算结果,在不同荷载等级下,考虑粘结应力传递模型的结果与不考虑粘结应力传递模型的计算结果相比,与试验值更接近。前者极限荷载和对应极限挠度的误差范围为-0.6%~1.8%和-10.5%~9.1%,后者极限荷载和对应极限挠度的误差范围为1.1%~6.1%和-11.4%~-2.2%。
3)考虑粘结应力传递的计算模型同样能较为精确地预测FRP抗弯加固锈蚀RC梁的荷载挠度曲线,极限荷载值的误差范围为-3.6%~4.2%,极限挠度误差范围为-4.2%~8.3%。
参考文献:
[1] AYKAC S, KALKAN I, AYKAC B, et al. Strengthening and repair of reinforced concrete beams using external steel plates [J]. Journal of Structural Engineering, 2013, 139(6): 929-939.
[2] 任伟, 贺拴海, 赵小星, 等. 黏贴钢板加固持荷钢筋混凝土T型梁模型试验[J]. 中国公路学报, 2008, 21(3): 64-68.
REN W, HE S H, ZHAO X X, et al. Model test on preloaded RC T-beam strengthened by bonded steel plates [J]. China Journal of Highway and Transport, 2008, 21(3): 64-68. (in Chinese)
[3] CHANG X, WU Y F. An analytical model for predicting the response of RC beams strengthened with strain localized steel plate [J]. Construction and Building Materials, 2015, 74: 140-150.
[4] 张建仁, 唐皇, 彭建新, 等. 锚贴钢板加固RC锈蚀梁承载力计算方法与试验研究[J]. 工程力学, 2015, 32(3): 97-103.
ZHANG J R, TANG H, PENG J X, et al. Caculation method and experimental study on corroded RC beams strenthened by steel plant anchored with stud [J]. Engineering Mechanics, 2015, 32(3): 97-103. (in Chinese)
[5] PENG J X, TANG H, ZHANG J R. Structural behavior of corroded reinforced concrete beams strengthened with steel plate [J]. Journal of Performance of Constructed Facilities, 2017, 31(4): 04017013.
[6] TANG H, PENG J X, ZHANG J R. Influence of further corrosion on structural behavior of corroded reinforced-concrete beam strengthened with steel plate using different strengthening schemes [J]. Journal of Performance of Constructed Facilities, 2020, 34(2): 04019117.
[7] 张建仁, 唐皇, 彭建新, 等. 钢板加固锈蚀RC梁短期挠度计算方法和试验[J]. 中国公路学报, 2015, 28(10): 41-50.
ZHANG J R, TANG H, PENG J X, et al. Calculating method and test research of short-term deflection of corroded RC beam strengthened by steel plate [J]. China Journal of Highway and Transport, 2015, 28(10): 41-50. (in Chinese)
[8] AL-SAIDY A H, AL-HARTHY A S, AL-JABRI K S, et al. Structural performance of corroded RC beams repaired with CFRP sheets [J]. Composite Structures, 2010, 92(8): 1931-1938.
[9] AL-SAIDY A H, AL-JABRI K S. Effect of damaged concrete cover on the behavior of corroded concrete beams repaired with CFRP sheets [J]. Composite Structures, 2011, 93(7): 1775-1786.
[10] TRIANTAFYLLOU G G, ROUSAKIS T C, KARABINIS A I. Effect of patch repair and strengthening with EBR and NSM CFRP laminates for RC beams with low, medium and heavy corrosion [J]. Composites Part B: Engineering, 2018, 133: 101-111.
[11] 王曉刚, 李森, 周新刚. 有弱界面的CFRP抗弯加固中U型箍防剥离研究[J]. 土木建筑与环境工程, 2014, 36(2): 14-20,27.
WANG X G, LI S, ZHOU X G. Effectiveness of U-strips to prevent CFRP debonding in strengthened RC beams with weak interfaces [J]. Journal of Civil,Architectural & Environmental Engineering, 2014, 36(2): 14-20,27. (in Chinese)
[12] HASKETT M, OEHLERS D J, MOHAMED ALI M S. Local and global bond characteristics of steel reinforcing bars [J]. Engineering Structures, 2008, 30(2): 376-383.
[13] LONG X, TAN K H, LEE C K. Bond stress-slip prediction under pullout and dowel action in reinforced concrete joints [J]. ACI Structural Journal, 2014, 111(4): 977-987.
[14] CAIRNS J, ABDULLAH R B. Bond strength of black and epoxy-coated reinforcement-A theoretical approach [J]. ACI Materials Journal, 1996, 93(4): 362-369.
[15] BHARGAVA K, GHOSH A K, MORI Y, et al. Suggested empirical models for corrosion-induced bond degradation in reinforced concrete [J]. Journal of Structural Engineering, 2008, 134(2): 221-230.
[16] WU Y Z, LV H L, ZHOU S C, et al. Degradation model of bond performance between deteriorated concrete and corroded deformed steel bars [J]. Construction and Building Materials, 2016, 119: 89-95.
[17] LIN H W, ZHAO Y X, OBOLT J, et al. Bond strength evaluation of corroded steel bars via the surface crack width induced by reinforcement corrosion [J]. Engineering Structures, 2017, 152: 506-522.
[18] 邓宗才, 李朋远. FRP加固钢筋混凝土结构阻锈性能的研究[J]. 北京工业大学学报, 2011, 37(6): 836-840.
DENG Z C, LI P Y. Anticorrosion performances of reinforced concrete structure retrofitted with FRP [J]. Journal of Beijing University of Technology, 2011, 37(6): 836-840. (in Chinese)
[19] SOUDKI K, SHERWOOD T. Bond behavior of corroded steel reinforcement in concrete wrapped with carbon fiber reinforced polymer sheets [J]. Journal of Materials in Civil Engineering, 2003, 15(4): 358-370.
[20] ZHOU Y W, DANG L J, SUI L L, et al. Experimental study on the bond behavior between corroded rebar and concrete under dual action of FRP confinement and sustained loading [J]. Construction and Building Materials, 2017, 155: 605-616.
[21] PAPAKONSTANTINOU C G, BALAGURU P N, AUYEUNG Y. Influence of FRP confinement on bond behavior of corroded steel reinforcement [J]. Cement and Concrete Composites, 2011, 33(5): 611-621.
[22] WANG X G, ZHANG W P, CUI W, et al. Bond strength of corroded steel bars in reinforced concrete structural elements strengthened with CFRP sheets [J]. Cement and Concrete Composites, 2011, 33(4): 513-519.
[23] CEB-FIP. CEB-FIP model code-design code [M]. London, UK, Thomas Telford, 1991.
[24] Building code requirements for structural concreteand commentary: ACI 318-05 [S]. Farmington Hills, USA. 2008.
[25] 张伟平, 商登峰, 顾祥林. 锈蚀钢筋应力应变关系研究[J]. 同济大学学报(自然科学版), 2006, 34(5): 586-592.
ZHANG W P, SHANG D F, GU X L. Stress-strain relationship of corroded steel bars [J]. Journal of Tongji University (Natural Science), 2006, 34(5): 586-592. (in Chinese)
[26] COLLINS M, MITCHELL D. Prestessed concrete structure [M]. Prentice Hall, NJ., 1991.
[27] 唐皇. 钢板加固锈蚀RC梁承载性能试验研究和理论分析[D]. 长沙: 长沙理工大学, 2017.
TANG H. Experimental research and theoretiacl analysis of bearing capacity of corroded RC beams strengthened by steel plate [D]. Changsha: Changsha University of Science and Technology, 2017. (in Chinese)
[28] 鄧文明. 氯盐环境下BFRP板加固钢筋混凝土梁受弯性能试验研究[D]. 南宁: 广西大学, 2016.
DENG W M. Experimental study on flexural performance of reinforced concrete beams strengthened with BFRP sheet under chloride condition [D]. Nanning: Guangxi University, 2016. (in Chinese)
[29] ZHANG X H,WANG L, ZHANG J R, et al. Model for flexural strength calculation of corroded RC beams considering bond-slip behavior [J]. Journal of Engineering Mechanic, 2016, 142(7):04016038.
(编辑 王秀玲)

