大跨度钢斜拉桥主梁监测挠度的评估与预警

刘小玲 黄侨 任远++樊叶华

摘要：在南京长江三桥长期监测数据的基础上，提出了一种基于统计理论的钢斜拉桥主梁挠度的长期趋势评估和动态预警设置方法.首先，分析挠度随温度的变化特征，选取夜间0：00-1：00时段的挠度数据，剔除车辆荷载的影响，并考虑整体升降温作用，进而得到恒载挠度评估指标的基准值.其次，采用线性适度模型和基于实质的灰色关联度法对挠度进行评估，以2007～2010年的数据为例，结果表明：本文的评估结果与长期变化趋势一致，挠度变化趋势有助于指导桥梁结构病害的进一步检查.最后，基于一定保证率建立桥梁跨中挠度黄、红两级预警线，考虑交通量变化及累积损伤带来的影响，设置动态预警线.通过2008年雪灾前后状况和交通量增长情况两个示例进行检验，结果表明：本文设置的动态预警线不仅能有效地应用于桥梁正常运营或突发状况，还能根据桥梁的实际状况实现同步更新.

关键词：钢斜拉桥；挠度；统计理论；评估；预警

中图分类号：U446.1 文献标识码：A

主梁挠度是桥梁长期监测中的一项直观且重要的指标.通过对结构几何形态的观测，可反演出结构的内力变化情况，进而为损伤的定位提供参考和依据.目前大跨径桥梁的主梁挠度监测方法众多，主要有连通管法、GPS法、倾角仪法、激光投射法、机器人监测法等[1].这些方法各有优劣，其中连通管法具有监测范围大、经济、不受现场恶劣环境的影响、可以实现多点同步监测的优点，发展前景良好.对于主梁挠度的评估、预警已有一些相关研究论文发表，包括挠度与温度的相关性分析[2-3]、线形评估预警[4-6]等方面.然而对于钢结构斜拉桥的挠度长期评估尚未见报道，预警线的设置亦各不相同，更无统一的标准可循.

本文以钢塔钢箱梁斜拉桥——南京长江三桥的长期变形监测数据为基础，在阐述主梁挠度的温度特征后，选择统一标准下的挠度评估指标，对长期状态下的挠度进行评估和预警值设置，并通过实测数据验证其可靠性.

1挠度的温度效应

1.1挠度监测布置概况

南京长江三桥是我国首座具有钢塔的钢箱梁斜拉桥，主跨648 m.该桥于2005年10月建成通车，次年其健康监测系统投入使用.南京三桥的主梁挠度监测采用的是封闭式连通管法.该方法是利用连通管内液面水平的原理，沿梁体布设连通管道，由压力波传递液位的变化，伴以高性能压力变送器检测液体压力的波动，换算得到桥梁挠度的变化值.

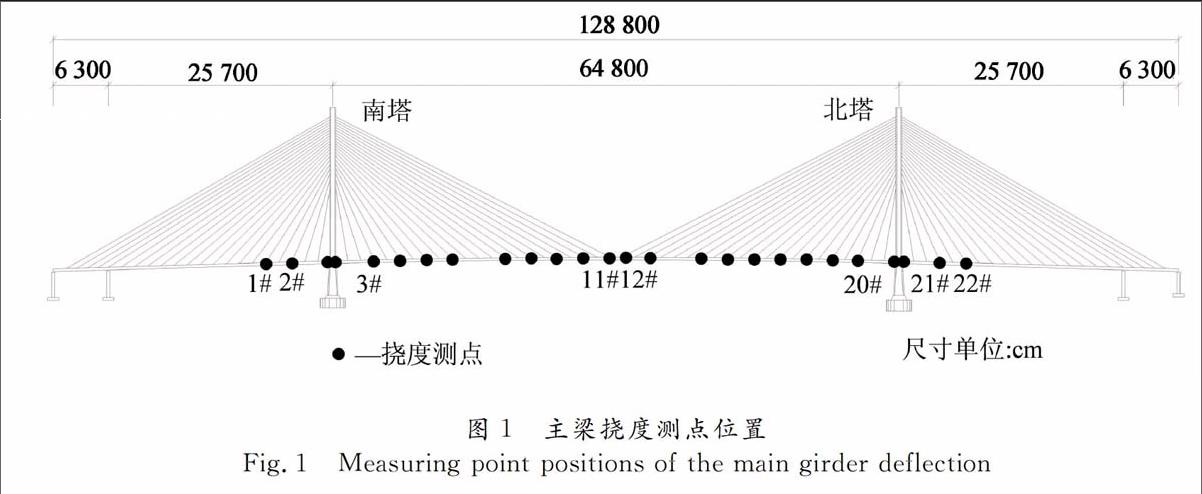
在该桥的边跨和中跨纵向均布置了相应挠度测点.以上游为例，有效测点共22个，位置分布如图1所示.主梁挠度测点采样频率是10 Hz.

1.2挠度的温度效应

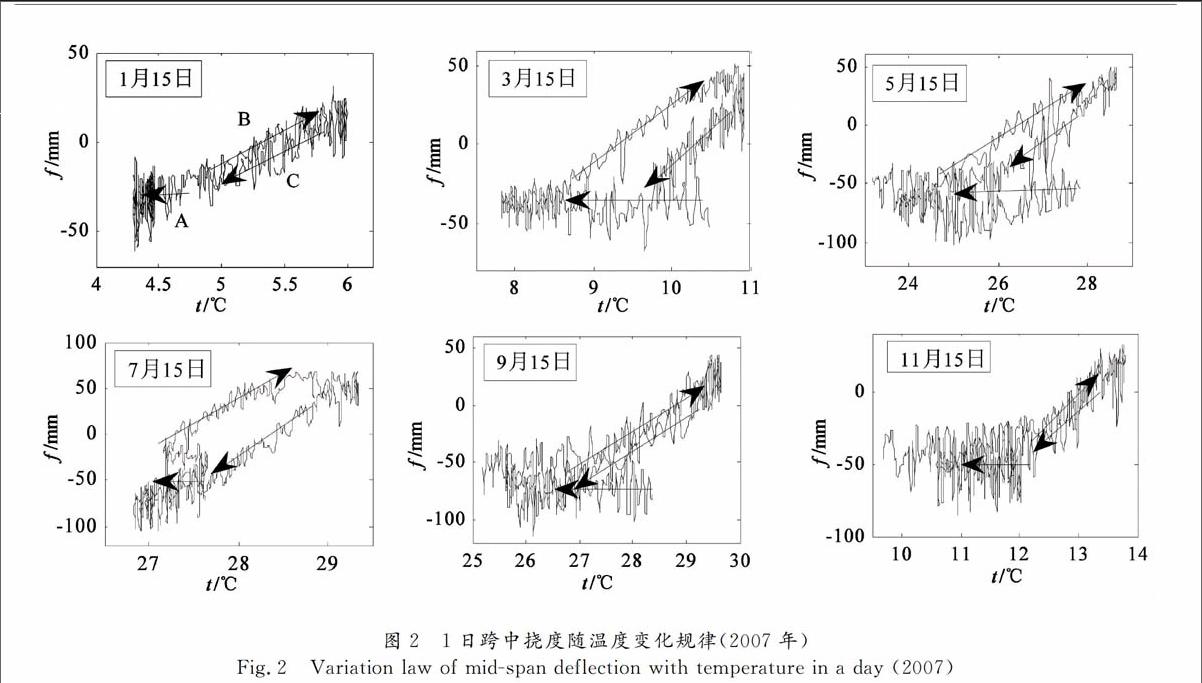
运营状态下影响斜拉桥跨中挠度变化的因素很多，其中最主要影响因素是温度作用和车辆荷载作用.如果将温度和车辆荷载作用效应剔除，可得到恒载下挠度长期评估的统一标尺.关于挠度的温度效应已有学者从理论推导和实桥监测方面做了相关的研究[7-8]，但是针对钢主梁和钢塔斜拉桥的特性较少报道.通过分析多年的挠度和温度监测数据，可以发现以下规律：1）挠度与温度的变化是同步的.文献[2]中针对混凝土梁斜拉桥的研究结论是跨中挠度和温度存在约2 h的滞后，而本文分析结果显示钢箱梁斜拉桥由于材料对温度反应敏感基本不存在滞后现象.2）挠度的变化周期为一天.一天内挠度变化主要分为两部分，一部分是夜晚时段，整体升降温作用较小；另一部分是白天时段，温度场的影响量较为可观，基本为线性.图2给出了2007年6个月每月15日的跨中挠度与温度的变化规律，规定负值表示主梁下挠，索塔处主梁挠度为0.

由图2看出，各个月一天内的跨中挠度与温度的变化规律较一致，以1月15日的数据为例，跨中挠度变化形成了典型的三阶段，分别定义为A、B、C三个阶段.第一阶段A：结构处在黑夜环境下，温度场较为平稳，因而变化率较平缓.此时段的挠度变化主要来自车辆荷载作用.值得注意的是其波动量大于白天，这是因为夜里行驶重车所致.第二阶段B：太阳辐射开始发挥作用并呈现持续加强状态，挠度变化率逐渐稳定到一个数值.第三阶段C：日照逐渐消失，大气温度渐渐降低，变化率和B阶段基本一致.

可见，夜间桥梁跨中挠度主要受整体升降温作用和车辆荷载作用.其中整体升降温的作用可通过对斜拉桥整体有限元模型施加温度荷载计算得到.对于车辆荷载作用，在夜间车流量较少，且多为重车过桥的时段，其车辆荷载效应可利用小波滤波剔除.统计结果表明，剔除活载效应后得到的恒载挠度值与该时段挠度的平均值非常接近.所以，本文在后续研究中，均以夜间0：00-1：00时段的挠度平均值作为当时温度下的恒载挠度计算值.

在剔除活载影响后，为对所有实测挠度数据统一分析评估，将所有温度统一至该桥合龙温度（24 ℃），温度差值部分造成的挠度变化通过斜拉桥整体有限元模型计算得到.最终得到恒载挠度评估指标的基准值.

2挠度的长期状态评估

2.1挠度评估方法

多个挠度测点数据属于序列数据，这类指标的变化包含基准线的平移变化和围绕基准线上下波动两种情况，即均匀变化和非均匀变化，挠度最终得分为两者相乘.

挠度的均匀变化是由多个测点的评分合成得到.在以往文献中，单个测点的限值一般采用计算跨径的1/500指标，多测点变权合成，这种方式的处理是面向桥梁适用性的.然而，恒载挠度是长期损伤累积过程，在各测点之间变化较为连续，不存在突变的情况，因而其变权作用并不明显.本文面向承载能力，以正常使用极限状态下的挠度计算值为上下限值，且不考虑变权，挠度的均匀变化得分计算如下：

F=1n∑ni=1yi. （1）

式中：F为挠度均匀得分（0≤F≤100）；n为挠度测点总数，yi为第i个挠度测点的评估值（0≤yi≤100），计算方法见公式（2）.

单个挠度测点的评分采用线性适度模型[9]，规定挠度为监测初始值时评分为100，超过正常使用极限状态下的挠度计算最大值和最小值以外时评分为0，其他值以适度指标模型线形插值得到.计算公式为：

yi=100x（min ）i-xix（min ）i-x（0）ix（min ）i

式中：x（0）i为第i个挠度测点的所选数据中最早监测值， xi为第i个挠度测点的当前监测值，x（max ）i，x（min ）i分别为正常使用极限状态活载短期效应组合下计算得到的挠度最大值和最小值.

若某个挠度测点缺少监测值，则令其评分为100分，权重为0，即该点的挠度不参与评估.

挠度的非均匀变化可采用关联度计算方法.在关联度计算方法方面，为满足关联度的传递性、对称性等基本性质，文中采用基于实质的灰色关联度[10]，而非斜率关联度.挠度的非均匀变化得分计算如下：

ξ=1n-1∑n-1k=1ωi（ω2i+1）ω4i+1. （3）

式中：ωi=（xi+1-xi）/（xi+1（0）-xi（0）），反映第i个和第i+1挠度测点之间的波动变化状况；ξ为基于实质的关联度，反映所有挠度测点的非均匀变化情况.

通过上述两步计算，挠度最终得分为F×ξ.

2.2应用实例

为检验上述方法的适用性和正确性，选取南京长江三桥2007年1月～2010年12月（48个月）监测数据对主梁挠度进行评估.每个月选取中旬的一天的0：00至1：00之间的挠度平均值作为代表.

图3给出了南塔岸侧和江侧以及北塔岸侧的挠度以2007年1月为初始时间点的长期变化趋势.北塔江侧变化趋势与南塔江侧一致，因此不再列出.图3（a）表明，北塔岸侧21#和22#测点出现轻微的上拱；图3（b）表明，南塔江侧出现比较大的下挠，尤其是11#测点，但各测点的变形逐渐趋于稳定；图3（c）表明，靠近南塔附近的测点（1#～4#测点）挠度值较为稳定（上述各测点位置参见图1）；图3（d）给出了2007年1月和2010年12月的整体主梁挠度对比.可见，恒载挠度的变化是一个长期、连续的过程，通过观察分析前期的趋势走向，在一定程度上可以实现趋势预测.同时，这些挠度测点数据的症状反映了结构的整体变形，可间接反映结构的潜在病害，养护单位宜进一步关注北塔变形、钢箱梁裂纹等状况.

分别采用本文建立的基于实质的灰色关联度评估方法以及基于斜率关联度的评估方法对2007年至2010年的挠度进行评估，详细评估结果如图4所示.依据《公路桥涵养护规范》（JTG H11-2004）中的技术状况分类界限，截止2010年12月，挠度均属于1类.结合图3趋势线来看，整体线形的波动状况与本文评分状况基本一致，即前期急速下降，后期下降变缓，因而本文评估方法具有较好的适用性.

3挠度的预警值设置

3.1预警线的设置

预警线的设定可为桥梁管理人员及时发现异常情况并快速处理提供重要警示[11].预警线的设定目前尚无统一的标准.常见的预警设置方法有以下几种，见表1.

表1中的“标准法”和“模型法”体现的是结构安全性和适用性因素，预警线值很大，而正常运营状态下主梁变动往往不会达到那样的限值，这使得挠度预警功能长期闲置；第三种“监测基准法”的基准值是采用监测系统初始设定零值，预警线采用超基准值10%，20%等来判定.然而这样的设置并无理论依据，且在实际使用过程中，这种预警值往往显得过小，而导致系统经常报警，失去了应有的预警意义.

因而有必要考虑一个更为合理的预警线设置方法.预警设置的目的在于不仅可满足日常运营状况的需要，还能在突发状况下有所反映，以便引起养护人员的关注，及时做出反应.长期监测数据属于序列指标，可以采用统计原理.基于一定保证率下的平均值μ和标准差σ的计算值作为预警线，其中保证率的选择是实际试算的结果.值得注意的是，考虑交通量呈现逐年增长的趋势[16]，统计指标也是逐年变化，为减少交通量变化及已有累积损伤带来的影响，建议选取拟预警桥梁前一年的挠度监测数据为样本.因而，本文建立的是动态预警线.预警设为两条，分别为黄色和红色预警线.表2分别给出了2007和2010年的预警线设置值.

本文的动态预警方法是建立在统计的基础上，具有较好的通用性，其他类型桥梁亦可参照使用.另外，预警线的设置仅需得到前一段时间的统计参数值（μ和σ），因而其操作较为简便.

下面分别给出正常状况，突发状况以及交通量增加状况下的预警线应用，将本文方法与“监测标准法”进行对比.对比结果见图5和图6.

3.2预警实例

2008年1月26日至2月1日，江淮大地普降大雪，南京遇到了50年未遇的大雪，这是对南京长江三桥结构的一次严峻考验.为检验本文建立的预警标准的实用性，以这几日的跨中挠度数据为例，将雪荷载也看成是一种临时性活载，验证预警系统的适用性.2008年1月24日至1月26日的挠度变化状况见图5.

首先需根据前期交通量状况，确定黄色和红色预警线.选取2007年的挠度监测数据为样本，计算预警线两个参数，得到黄色预警线为-85 mm，红色预警线为-120 mm.

图5给出了两种预警线，实线代表本文建议的方法，虚线代表上述“监测基准法”，细线为相应黄色预警线，粗线为相应红色预警线.表1的前两种方法

因为黄线较大，黄线早已超出图5中的范围，不能较快地反映结构的变位，因而不再列出.从图5可以看出，1月24日和1月25日期间，结构处于正常状态，“监测基准法”的黄色预警在夜间启动，出现报警太频繁的现象.1月26日凌晨开始下雪，中午之后雪荷载已达到一定的量值，挠度达到了本文方法的

黄色预警线，之后挠度值逐渐超过本文方法的红色预警线.此时宜考虑雪势的发展和桥面荷载状况，宜立刻采取控制车辆通行、除雪等措施.1月26日下午2点15分开始封桥，后期养管单位有秩序地进行了除雪工作.

图6给出了2007年和2010年的同时段（3月25日-30日）挠度监测数据，其中细线、粗线分别为黄色与红色预警线.可以看出，2010年相比2007年，恒载挠度已经出现轻微下挠，和第2节的挠度评估结果较为一致.另外，由于交通量的增长，活载产生的效应更大.如果仍采用2007年设定的预警线，则报警频繁，而本文建立的2010年预警线相较之前而言，整体下移，且两条预警线之间的区间更大.可见，该预警线能够较好地适应活载增长及结构自身变化带来的影响.

综上，本文设置的动态预警线不仅能有效地应用于桥梁正常运营或突发状况，还能根据桥梁的实际状况实现同步更新.

4结论

通过对大跨径钢结构斜拉桥——南京长江三桥长期挠度监测数据的分析，可得到以下结论：

1）一天内的跨中挠度变化具有典型的三阶段变化特征，夜间桥梁跨中挠度主要受整体升降温作用和车辆荷载作用.选取夜间0：00-1：00时段的挠度数据，剔除车辆荷载的影响，并考虑整体升降温作用，可得到恒载挠度评估指标的基准值.

2）通过关注长期趋势线以及基于实质的灰色关联度法对2007-2010年期间的挠度进行评估，结果表明整体线形的波动状况与本文评分状况基本一致.主梁跨中出现轻微下挠、北塔岸侧的边跨略有上拱的趋势，养护单位宜进一步关注北塔倾斜变形的可能性.

3）对比已有的三种预警线设置方法，本文基于一定保证率建立桥梁跨中挠度黄、红两级动态预警线，通过2008年雪灾前后状况和交通量增长情况两个示例检验了该预警线设置方法的适用性和合理性.本文的动态预警方法具有较好的通用性和简便性，其他类型桥梁亦可参照使用.

参考文献

[1]KOHUT P， GASKA A， HOLAK K， et al. A structure's deflection measurement and monitoring system supported by a vision system[J]. TmTechnisches Messen， 2014， 81（12）： 635-643.

[2]殷新锋， 邓露. 随机车流作用下桥梁冲击系数分析[J]. 湖南大学学报：自然科学版， 2015， 42（9）：68-75.

YIN Xinfeng， DENG Lu. Impact factor analysis of bridges under random traffic loads [J]. Journal of Hunan University： Natural Sciences， 2015， 42（9）：68-75.（In Chinese）

[3]BARR P J， STANTON J F， EBERHARD M O. Effects of temperature variations on precast， prestressed concrete bridge girders[J]. Journal of Bridge Engineering， 2005， 10（2）： 186-194.

[4]曾威，于德介，胡柏学，等.基于连通管原理的桥梁挠度自动监测系统[J].湖南大学学报：自然科学版，2007，34（7）： 44-47.

ZENG Wei， YU Dejie， HU Baixue， et al. An automonitoring system based on the communicating pipe principle of bridge deflection[J]. Journal of Hunan University： Natural Sciences， 2007， 34（7）： 44-47. （In Chinese）

[5]伍华成，项贻强. 基于变权综合原理的斜拉桥索力、线形状态评估[J]. 中国铁道科学， 2006， 27（6）： 42-48.

WU Huacheng， XIANG Yiqiang. Assessment the cable tension and the linetype state of cablestayed bridge based on variable weight synthesis[J].China Railway Science， 2006， 27（6）： 42-48. （In Chinese）

[6]SOUSA H， CAVADAS F， HENRIQUES A， et al. Bridge deflection evaluation using strain and rotation measurements[J]. Smart Structures and Systems， 2013， 11（4）： 365-386.

[7]刘夏平，杨红，孙卓，等. 基于LSSVM的桥梁挠度监测中温度效应分离[J]. 铁道学报， 2012， 34（10）： 91-96.

LIU Xiaping， YANG Hong， SUN Zhuo， et al. Study on separation of bridge deflection temperature effect based on LSSVM [J]. Journal of the China Railway Society， 2012， 34（10）： 91-96. （In Chinese）

[8]李嘉，冯啸天，邵旭东，等. 正交异性钢桥面RPC薄层组合铺装体系研究[J]. 湖南大学学报：自然科学版， 2012， 39（12）： 7-12.

LI Jia， FENG Xiaotian， SHAO Xudong， et al. Research on composite paving system with orthotropic steel bridge deck and thin RPC layer [J]. Journal of Hunan University： Natural Sciences， 2012， 39（12）： 7-12. （In Chinese）

[9]HUANG Q， REN Y， LIN Y Z. Application of uncertain type of AHP to condition assessment of cablestayed bridges [J].Journal of Southeast University： English Edition， 2007， 23（4）： 599-603.

[10]李宏艳. 关于灰色关联度计算方法的研究[J]. 系统工程与电子技术，2004， 26（9）： 1231-1233.

LI Hongyan. Study on the calculation method of grey relationship degree [J]. Systems Engineering and Electronics， 2004， 26（9）： 1231-1233. （In Chinese）

[11]KALOOP M R， LI H. Monitoring of bridge deformation using GPS technique[J]. Ksce Journal of Civil Engineering， 2009， 13（6）：423-431.

[12]中交公路规划设计院有限公司. JTG D60-2015， 公路桥涵设计通用规范[S]. 北京： 人民交通出版社股份有限公司， 2015.

CCCC Highway Consultants Co.， Ltd. JTG D60-2015， General specifications for design of highway bridges and culverts [S]. Beijing： China Communications Press Co.， Ltd， 2015. （In Chinese）

[13]LAN Z， YANG X， CHEN W， et al. Study on noncontact weightedstretchedwire system for measuring bridge deflections and its effect factors [J]. Engineering Structures， 2008， 30（9）：2413-2419.

[14]SURYANITA R， ADNAN A. Earlywarning system in bridge monitoring based on acceleration and displacement data domain [M]. Berlin in Germany： Springer Netherlands， 2014：157-169.

[15]王凯. 基于时间序列分析的桥梁损伤预警研究[D]. 西安：长安大学公路学院， 2008.

WANG Kai. A research about early warning of bridge damage based on time series analysis [D]. Xi'an：Highway College of Changan University， 2008. （In Chinese）

[16]BELL E S， LEFEBVRE P J， SANAYEI M， et al. Objective load rating of a steelgirder bridge using structural modeling and health monitoring[J]. Journal of Structural Engineering， 2013， 139（10）：1771-1779.