直升机双速传动系统换挡过程冲击度研究
陈志刚,陈召光,刘志辉
(1.邵阳学院 机械与能源工程学院,湖南 邵阳,422000;2.邵阳学院 高效动力系统智能制造湖南省重点实验室,湖南 邵阳,422000)
目前,在直升机领域,关于提升直升机的巡航性能,其关键要素是油耗问题。针对巡航油耗的改善问题,现有技术主要是通过改变主旋翼的转速来实现,而主旋翼的转速改变有两种:一种是调整涡轴发动机的输出转速;另一种是用双速传动机构来改变输出转速。发动机的输出转速的变化仅为总输出转速的15%左右,而双速传动机构的输出转速变化可高达总输出转速的50%。现有的发动机变转技术还不够成熟,而双速传动机构的变转技术成熟度相对较高。因此,为了提高直升机的工作性能和巡航时间,双速传动系统是目前改变主旋翼转速的最经济性的方式[1-2]。双速传动系统在换挡过程中,避免不了换挡带来的冲击所引起的振动跟噪声,影响其换挡品质,现有的变速系统换挡研究多存在于汽车领域。在直升机领域,国外AHIMI MOUSAVI等[3]利用行星轮系的功率和运动方程以及机构的自由体图建立的动力学模型,只适用于稳态或者短时间内的转矩波动,不适用于整个换挡过程。国内外对变速换挡的研究才刚刚起步,换挡过程分析的动力学模型考虑得还不够细致,还存在许多不足,所以,一些直升机企业越来越重视双速自动变速器的换挡研究。
本文将结合拉格朗日方程和虚功原理建立变速器行星轮系的数学模型,通过接合特性,推导离合器转矩与液压执行机构的数学模型,分析负载旋翼及发动机的转矩模型,设定离合器充油信号,建立换挡动态仿真模型,分析换挡过程中离合器充油快慢对系统冲击度的影响。
1 行星轮系动力学模型
某型双速系统的变速器结构见图1,忽略变速器内部的润滑阻尼和齿轮啮合刚度对系统动力学的影响。

1—输入轴;2—齿圈1;3—齿圈2;4—行星轮;5—输出轴;6—机匣;7—楔块式超越离合器图1 变速器结构简图Fig.1 The transmission structure
1.1 单个行星轮系动力学模型
单个行星排由太阳轮、行星轮、内齿圈及行星架组成。行星齿轮组的运动过程可由4个参数表示,它们分别是太阳轮、行星架、行星轮和齿圈的角位移(α,β,γ和θ),假设太阳轮、行星轮和齿圈之间相互啮合,不出现滑移[4]。根据行星轮系各部件的啮合关系以及相互啮合处的线速度大小相等,得到以下式子:
(1)
(2)
式(1)和式(2)中:rs为太阳轮分度圆半径;rr为齿圈分度圆半径;rp为行星轮分度圆半径;rc为行星架半径。
1.2 变速器行星轮系动力学模型
按照上述的行星轮系运动学关系,将式(1)和式(2)引入到行星轮系中,该行星齿轮组的运动过程可由5个参数表示,它们分别是太阳轮、行星架、行星轮、齿圈1和齿圈2的角位移(α,β,γ,θ1和θ2)。选择α,β作为独立变量,则行星轮系运动关系可表示为
(3)
通过代数变换可以获得其他部件的转速之间的关系:
(4)

引入拉格朗日方程[5],结合双速行星轮系的运动学方程,该行星轮的总动能为E=Eks+Ekc+Ekp+Ekr1+Ekr2。其中,系统动能包括了行星轮系中每个构件的动能,将独立变量α和β表示的角位移关系代入到系统动能表达式中,太阳轮、行星架及齿圈受到的转矩Ts,Tr1,Tr2和Tc会产生虚功。利用虚功原理[6],代入到拉格朗日方程中,可以得到关于(α,β)为独立变量的行星轮系机构的动力学模型:
(5)

2 换挡过程系统模型的建立
2.1 离合器模型建立
湿式离合器接合充油过程由液压执行机构来完成,通过油压作用在活塞上的接合压力使摩擦片与钢片产生滑动摩擦,持续到摩擦片与钢片的相对转速为零,即湿式离合器接合过程结束,针对最优充油油压曲线进行建模,即:
(6)
式中:p0为最大接合压力,p0=1.5 MPa;ts为压力迟滞时间,取ts=0.25 s。
液压缸的密封圈摩擦阻力Ff:
Ff=0.03F
(7)
式中:F为充油力。
湿式离合器的摩擦片压紧力为
(8)
式中:R1为液压缸内径;R2为液压缸外径;Δp为排油压力。
离合器摩擦面呈环状,湿式离合器粗糙转矩Tr2的计算方程[7]为
(9)
式中:n为摩擦片组数;Ri和Ro分别是摩擦片环面内径和摩擦片环面外径;μ为动摩擦系数。
超越离合器的转矩模型:
(10)
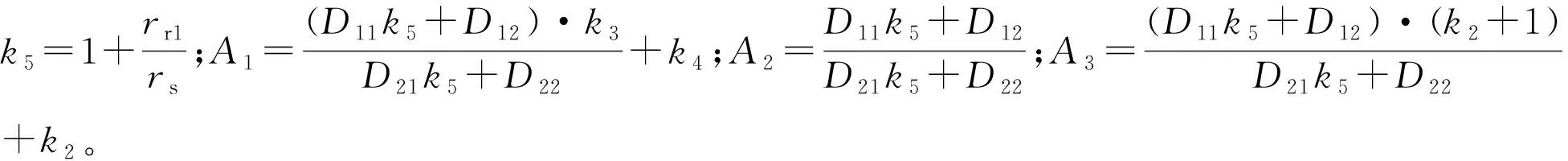
2.2 负载模型建立
根据直升机理论,直升机在升挡时,处于巡航阶段。降挡时,处于悬停阶段。因此,直升机在飞行过程中,受到旋翼叶片上的空气阻力、巡航时的机身空气阻力以及滚动阻力的影响。
直升机在升挡过程中,由巡航阶段到悬停阶段的转变,因此,等效负载阻力矩存在旋翼叶片阻力矩和滚动阻力矩[8-9],总阻力矩为
(11)
式中:Cq为阻力矩系数;ρ为空气密度;A为螺旋桨旋转面面积;Rrad为螺旋桨半径;ωf为旋翼轴转速;Cm为滚动力矩系数;δm为直升机旋转质量换算系数。
2.3 发动机模型建立
涡轮发动机动态输出扭矩特性可由实验数据和外特性曲线得[10-14],即:
(12)
(13)

本研究的换挡节气门开度为0.6,此时转速转矩实验数据见图2。
3 仿真结果分析
依据拉格朗日方程建立的系统动力学模型,可以得到双速传动系统的各构件转矩、转速以及系统的冲击度。应用MATLAB/Simulink模块分别建立发动机、变速器、负载系统模型,模拟旋翼机在t=2 s时从1挡升入2挡的过程。模拟过程中保持节气门开度为0.6的情况下,离合器液压执行机构油压见图3,即使换挡完成,油压依旧呈上升趋势,直至不变,系统相关参数的仿真结果见图2~8。

图2 发动机转速转矩数据图Fig.2 Engine speed torque data chart
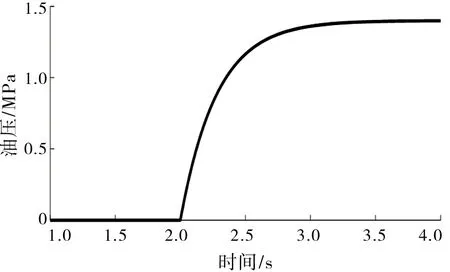
图3 液压执行机构油压Fig.3 Oil pressure of hydraulic actuator

图5 离合器转矩Fig.5 Clutch torque
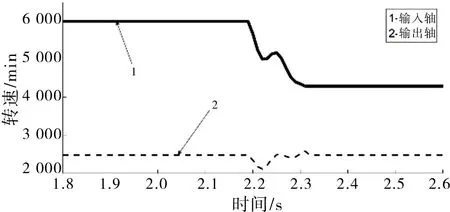
图6 输入轴、输出轴转速Fig.6 Input shaft and output shaft speed
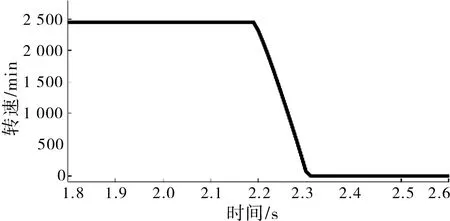
图7 齿圈2转速Fig.7 Speed of ring gear 2

图8 负载转矩Fig.8 Load torque
仿真结果不仅能够观测行星系统中所有构件的转速情况,还能够根据离合器执行机构控制的油压观测双速传动系统的发动机、负载扭矩和系统冲击度的情况。仿真模型实时体现了系统的响应状况:超越离合器转矩均由换挡开始直至下降至0,即超越离合器超越脱开,湿式离合器由换挡开始上升,经过回调至稳定值,即湿式离合器完全接合,换挡完成。输出轴转速即负载转速的换挡前后的转速保持不变,但换挡构成存在转速的波动。齿圈2的转速在升挡过程中缓慢减少到0。负载转矩在换挡前后,转矩值明显下降,符合换挡特性,但存在波动,从而产生系统冲击度。
如图9所示,改变p0值,使其换挡过程时间发生改变,以ps1对应p0值为1.40;ps2对应p0值为1.45;ps3对应p0值为1.50;ps4对应p0值为1.55;ps5对应p0值为1.60。分析可得,充油时间越长,系统前程冲击度越小,而后程冲击度幅度极值存在无规律差异,当p0值为1.40时,冲击度j最大值为-105 ms-3;当p0值为1.50时,冲击度j最大值为-107 ms-3;增幅为1.9%;当p0值为1.60时,冲击度j最大值为-112 ms-3,增幅为6.7%。因此,较少适当的p0值,延长换挡时间,可以有效地降低冲击度。
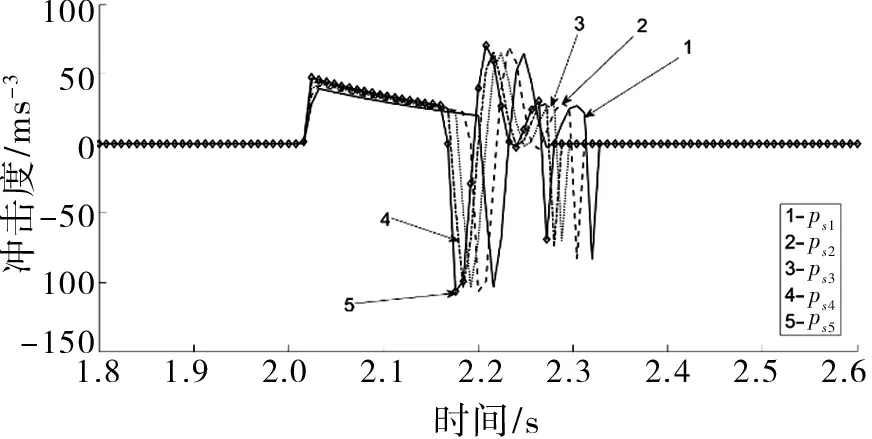
图9 不同充油信号的系统冲击度Fig.9 System impact of different oil filling signals
4 结论
1)利用拉格朗日方程和虚功原理,得到各轴角加速度运动方程,并基于发动机的试验数据,建立了发动机模型,根据换挡特性,设定离合器充油曲线。
2)基于MATLAB/Simulink软件平台,建立了双速传动系统仿真模型,对整机换挡过程进行了仿真,得到各构件转速转矩变化过程,分析了离合器之间的转矩关系,并分析了其他参数变化所对应的系统状态。
3)建立5种充油曲线,以改变其换挡时间,分析了5种充油信号对系统的冲击度影响。发现p0值为1.4时,冲击度极值最低,从而得到,p0值越接近接合油压值,冲击度越低。因此,减少p0值,延长换挡时间,可有效降低冲击度,提高换挡品质,为研究直升机双速系统换挡特性提供了完整的数学模型及理论基础,对于提高直升机其工作性能、改善其振动噪声具有较重要的意义。

