定数截尾试验下Pareto分布参数的条件Γ-minimax估计
周巧娟
(南京审计大学金审学院 基础部,江苏 南京,210023)
帕累托(Pareto)分布是意大利经济学家Pareto研究经济问题时提出的,在经济、军事、可靠性分析等诸多领域中均有广泛应用。关于该分布的研究引起了学者们的广泛关注。韩明[1]在平方损失和熵损失下讨论了Pareto 分布中形状参数的Bayes 估计和多层Bayes估计,研究了其容许性等。徐宝等[2]在加权p,q对称损失函数下,研究了Pareto分布形状参数的最小风险同变估计、广义Bayes估计及最大最小估计,并研究了三者之间的关系。朱宁等[3]在尺度参数已知的情况下,得到了复合MLINEX对称损失函数下Pareto 分布形状参数θ的Bayes估计,并证明了其可容许性。魏艳华等[4]利用混合Gibbs算法给出了定数截尾试验下Pareto 分布参数的Bayes估计。李如兵等[5]在移动极值排序抽样下,针对共轭先验及Jeffreys先验,在多种损失下获得了Pareto分布形状参数的Bayes估计。这些成果大多是在不同损失下,运用各种抽样数据对Pareto分布形状参数的Bayes估计进行了研究,但关于Pareto分布参数的稳健Bayes估计的成果却不多见。
在Bayes方法的稳健性分析中,选择一个先验分布类是处理先验分布不确定性的常用方法,条件Γ-minimax估计是在给定一类先验分布族Γ的条件下得到的一种稳健Bayes估计。本文在对称熵损失函数下,讨论了Pareto分布形状参数的条件Γ-minimax估计问题。
1 Pareto分布形状参数的条件Γ-minimax估计
1.1 对称熵损失函数
PODDER提出MLINEX损失函数[6],其定义为
(1)
这是一类非对称损失函数,金秀岩[7]在MLINEX损失函数的基础上,提出了复合MLINEX对称损失函数:
(2)
该损失函数为对称的非负严格凸函数,当ω=1,c=1时,式(2)为
(3)
此为对称熵损失函数[8]。这种损失具有对称性,即待估参数与其估计二者交换位置不会影响其函数形式。并且在该损失函数下,参数的稳健Bayes估计的求解要比一般的损失函数简单得多[9]。
1.2 Pareto分布形状参数的条件Γ-minimax估计
设Bayes统计推断中所采取的决策为δ=δ(x),损失函数为L(θ,δ(x)),x为子样,f(θ|x)为在子样x之下θ的后验概率密度,ρ(f(θ|x),δ)为采取决策δ的后验期望损失,即
ρ(f(θ|x),δ)=Ef(θ|x)[L(θ,δ(x))]。
条件Γ-minimax估计(CGM)最初是由WATSON[10]提出的,其定义为
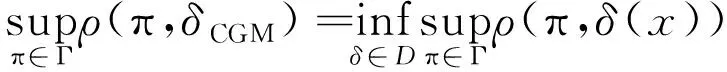
MECZARSKI对其计算规则进行了研究,给出了求解条件Γ-minimax估计的关键定理:
定理1[11]定义函数r(α,a)=ρ(πα,a),若该函数满足以下几个条件:
1)对于任何给定的α,r(α,a)对a是严格向下凸的。
2)对于任何给定的a,αmin(a)是r(α,a)的唯一极小值点,且是a的严格单调函数。
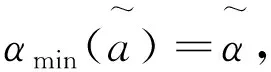

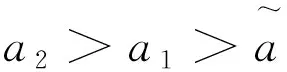
4)r(α1,a)-r(α2,a)是a的单调函数。
则满足r(α1,a*)=r(α2,a*)的a*即为a的条件Γ-minimax估计。
下面,将利用定理1讨论Pareto分布形状参数θ的条件Γ-minimax估计问题。
设随机变量X服从Pareto分布,其密度函数为
f(t;α,θ)=θαθt-(θ+1)
(4)
其中,α是尺度参数;θ是形状参数,且0≤α≤t,θ>0。
现有一批产品,寿命服从Pareto分布,共有n个,进行定数截尾试验,直到有r个失效为止,记失效时刻为t1≤t2≤…≤tr,则(t1,…,tr)的联合密度函数为
(5)
假设α已知,当样本t1,t2,…,tr为已知时,T为常量,所以,式(5)中参数仅为θ,取θ的先验分布为伽玛分布
(6)
由式(5)和式(6)可得θ的后验密度函数为
它仍为伽玛分布。
在对称熵损失函数式(3)下,选取决策δ的Γ-后验期望损失为
(7)
定理2取Pareto分布形状参数θ的先验分布族Γ1为
Γ1={π(θ;a,b)=Γ(a,b),a=a0,b1≤b≤b2,θ>0}
(8)

证明:该结论只需要证明,当π∈Γ1时,选取决策δ的Γ-后验期望损失
满足定理1的4个条件即可。

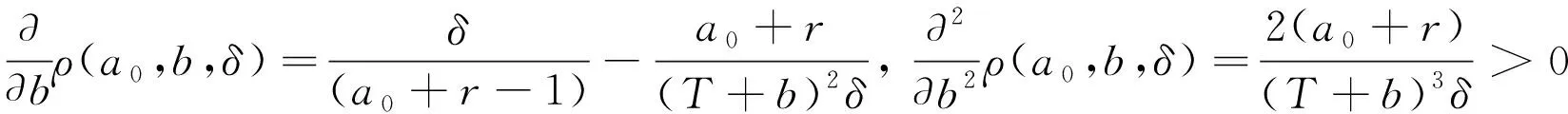
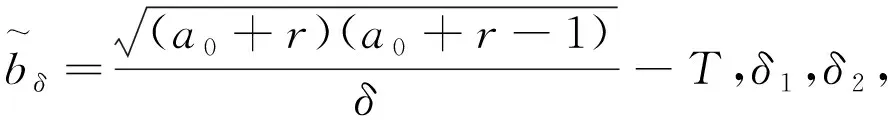


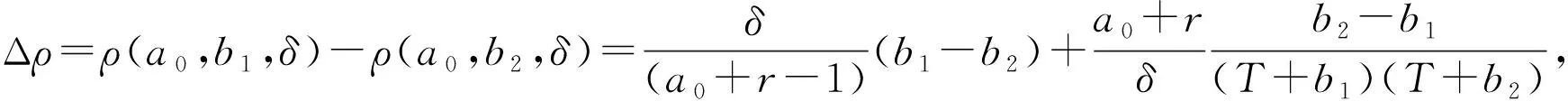
(9)
由式(9)可以看出:Δρ是δ的单调函数。

解得
(10)
定理3取Pareto分布形状参数θ的先验分布族Γ2为
Γ2={π(θ;a,b)=Γ(a,b),b=b0,a1≤a≤a2,θ>0}
(11)

证明:当π∈Γ2时,选取决策δ的Γ-后验期望损失为

解得
(12)
2 稳健性评价
关于条件Γ-minimax估计的稳健性评价,可沿用BERGER[12]的风险分析作为稳健性分析的基本方法。
决策δ(x)下的后验期望损失为ρ(π,δ(x)),那么决策δ(x)的稳健性指标为
(13)
由上式可知:若对任意取的值ε有
|RΓ(f(θ|x),δ)|<ε,
成立,则称该估计是ε稳健的。
因此,可以根据以上评价稳健性的指标来评价条件Γ-minimax估计稳健性的好坏。
3 随机模拟例子
假设有n=25个产品,寿命服从Pareto分布,其中,α=5,待估参数θ的真值为0.5,进行定数截尾试验,直到有r=20个失效为止,通过Monte-Carlo方法产生服从U(0,1)的随机数U1,U2,…,U20,再由ti=5/(1-Ui)2产生20个服从Pareto分布的随机数t1~t20分别为:17.786 5,20.472 2,51.496 2,7.675 7,9.475 9,920.523 8,8.537 0,6.575 6,14.491 1,37.468 9,7.463 3,14.038 2,51.628 7,11.003 3,849.922 4,84.745 2,13.940 0,7.736 9,13.902 8和6.994 3,那么可算得T=56.601 1,取θ的先验分布族分别为
由定理2和定理3的结论可得模拟结果,见表1。

表1 α已知时各分布族下θ的估计及损失 (真值α=5,θ=0.5)

4 结语
本文在对称熵损失函数下,给出了定数截尾试验下Pareto分布尺度参数α已知时,形状参数θ的一种稳健Bayes估计——条件Γ-minimax估计。随机模拟例子表明,由该方法得出的估计精度较高且具有稳健性,因而更有利于Pareto分布在各领域中的应用。

