聚类成员簇个数的选择方法研究

王江峰，徐 森，徐秀芳，花小朋，皋 军，安 晶

（盐城工学院 信息工程学院，江苏 盐城 224002）

聚类分析是在没有先验知识的情况下进行的，即训练样本的真实标签未知，仅根据数据的内在特性及规律，将训练样本进行分组。聚类分析的主要目标是将数据集（也称为模式集、点集或对象集）划分为自然组或簇，使得属于同一簇的对象相似，属于不同簇的对象不相似［1］。目前，聚类分析已广泛应用于心理学［2］、医学［3］、模式识别、信息检索、机器学习和数据挖掘等领域。

各种聚类算法接连被提出，聚类算法得到了不断改进，但找到适合所有数据集的聚类算法几乎是不可能的。为了在没有先验知识的情况下组合数据分区和产生一个更好的聚类结果，文献［4］提出了聚类集成的概念。聚类集成是为了提高聚类结果的准确性、稳定性和鲁棒性的一种算法［5］，通过将多个基聚类结果集成可以产生一个更优的结果。聚类集成将数据集的不同聚类结果组合成最终的聚类结果。单一的聚类算法有其自身的缺点，会导致一种算法只适用于特定的某一类数据集。聚类集成将这些聚类算法结合起来，可以在一定程度上弥补单一聚类算法的不足。相较于单一聚类算法，聚类集成既适用于更多的数据集，也抗噪声和离群值［6］。近年来的研究主要集中在3 个方面：（1）聚类成员生成，即如何获取精度较高且具有多样性的聚类成员。（2）聚类成员选择，即如何选出精度较高且差异性较大的聚类成员。（3）共识函数设计，即如何将聚类成员组合为精度更高的一致聚类结果。

研究指出，簇个数k 对聚类集成的结果有很大的影响［7-8］。然而，目前尚无关于聚类成员簇个数选择方法的系统研究和比较。因此，本文对不同的簇个数设置方法进行了比较研究，为聚类成员生成研究提供了有益的参考。

1 相关工作

在已有的聚类集成算法中，对于簇个数的选择方式有很多，大多数方法都是在给定的区间内随机选择簇个数，但对其设置方法的解释非常有限，也缺少对不同设置方法优劣的比较。

Li等［9］认为聚类成员的簇个数应该大于真实类别数，因此将其设置为k=min｛ n，50｝，其中n为对象个数。Bai 等［10］将每个聚类成员中的簇个数设置为每个给定数据集上的真实类别个数，这也是聚类集成研究中最常用的方法。由于使用相同的聚类算法，且每种算法生成的簇个数相等，聚类成员的差异只是由不同的初始聚类中心引起的，聚类集体往往缺乏多样性。为了增强聚类成员的多样性，研究人员提出了很多簇个数的随机取值区间，包括Liu 等［17］针对较大的数据集，簇个数在［2，2k］内随机选取，而其他数据集则在［k，］范围内随机选取。Zhou 等［18］针对较小的数据集设定簇个数等于真实类别个数，而其他数据集则在［2，M］范围内随机选取，其中M= min｛，50｝。徐森等［19］使用了两种不同的方法来生成聚类成员，分别是：（1）k=k*；（2）k从区间［2，2k*］中随机选择。

2 研究方法

设数据集X=｛x1，x2， …，xN｝，其中xi∈ℝδ，ℝ 为实数集，δ是特征个数，i=1，...，N。首先，本文预设簇个数的选择区间，以确保所有聚类成员簇个数都在相同取值范围内随机选择，不妨假设降维后的数据为Y=｛y1，y2， …，y N｝，其中yi∈ℝd，d是降维后的维度，i=1，...，N；其次，设计K-means聚类算法对数据集Y进行聚类，生成聚类成员，重复该步骤直至获得r个聚类成员；最后，使用Ward 层次聚类算法［20］对这r个聚类成员集成，获得最终的聚类结果。研究流程如图1 所示，下面分别对这3个步骤详细描述。

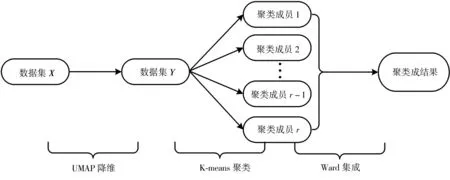
图1 聚类集成算法流程图Fig. 1 Flow chart of cluster ensemble algorithm

2.1 维数约简

维数约简通过降低数据复杂性来提高数据质量，可以有效解决维数灾难问题［21］。近年来，t-SNE因其能有效地识别数据中的局部结构而成为最常用的降维技术［22-23］。2018 年，Mcinnes 等［24］提出了一种全新的降维算法——一致流形逼近与投影（uniform manifold approximation and projec⁃tion for dimension reduction，UMAP）。UMAP 使用了拉普拉斯特征映射初始化和交叉熵目标函数，因而在保留全局结构方面优于t-SNE［25］。

UMAP 是一种建立在黎曼几何和代数拓扑的理论框架上的非线性降维方法。UMAP 一定程度上类似于t-SNE，在数据可视化方面有着较好的效果。与t-SNE 相比，UMAP 能够能更好地保存全局结构，比t-SNE有着更好的连续性，运行速度更快，且嵌入维数也不受计算限制。因此，本文在聚类成员生成阶段引入UMAP进行降维。

UMAP 的第一步骤是加权kw邻域的构造；第二步骤是找到一个低维的表示来优化交叉熵目标函数。第一个步骤中，计算每一个xi在指定维度下的kw最近邻，使得局部连通性约束ρi和归一化系数σi分别定义为：

加权有向图定义为Gˉ=（V，E，ω），其中V是顶点集，E={(xi，xj)|1 ≤h≤k，1 ≤i≤N}是边的集合，边的权重ω定义如下：

设A为加权有向图Gˉ的加权邻接矩阵，其对称矩阵B可通过下式获得：

第二个步骤中，UMAP 在低维空间中使用了力导向图布局算法，对沿边和顶点之间施加引力和斥力。最小化两个模糊集(A，u)和(A，v)的交叉熵目标函数C，其中，u和v为成员强度函数，C的定义如下：

最后使用随机梯度下降来优化模糊集交叉熵。

2.2 聚类成员生成

指定簇个数的选择范围，对降维后的数据使用K-means算法进行聚类，产生聚类成员。

K-means算法是一种基于原型和划分的聚类技术，根据k′集合来寻找最优质心。首先选择k′个初始质心，其中，k′是指定的参数，即期望的簇个数，每个点都被指派到距离其最近的质心所在的簇；然后更新每个簇的质心。重复指定和更新步骤，直到质心不再变化为止或迭代次数t达到指定阈值。

在相同的簇个数选择区间内重复运行Kmeans 算法r次，来获得r个聚类成员。在每个选定的簇个数范围内，可以得到r个聚类成员。

2.3 聚类集成

Ward 连接是最符合聚类目的的连接，因此也是最有效的连接［26］。与其他层次聚类一样，Ward连接从个体点开始，相继合并两个最接近的簇，直到只剩下一个簇。对于Ward连接，两个簇的邻近度定义为两个簇合并时导致的平方误差的增量。两个簇CA和CB之间的Ward 距离由下式给出：

式中：a和b分别是CA和CB的质心，nA和nB分别是CA和CB中数据点的数量。

综上，本文算法主要步骤如Algorithm 1所示。

Algorithm 1：

输入：数据集X

输出：聚类集成结果

1. 根据式（1）、式（2）、式（3）构建模糊集

2. 利用式（4）将模糊集表示为对称规范化加权邻接矩阵

3. 用随机梯度下降法优化式（5）中的交叉熵目标函数

4.Settto 1

5.repeat

6. 选择k′个初始质心

7. 将所有点分配到最近的质心

8. 更新每个簇的质心

9. 重复步骤7和8直至质心不再发生变化

10.t=t+1

11.untilt>20

12. 计算两个簇之间的邻近度

13.repeat

14. 合并最接近的两个簇

15. 更新邻近度矩阵，以反映新的簇与原来的簇之间的邻近性

16.until仅剩下一个簇

3 实验

3.1 数据集

本文实验中使用了5 个取自UCI 机器学习库的真实数据集，即Ecoli，Pen Digit（PD），Semeion，Multiple Features（MF），ISOLET，其详细信息如表1所示。

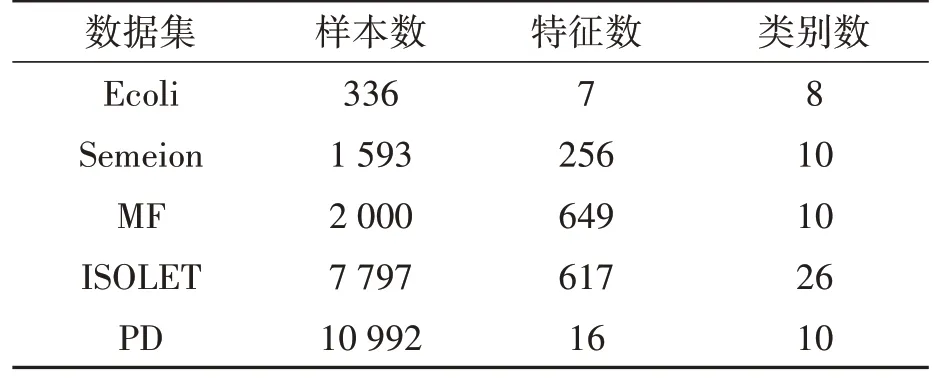
表1 数据集的描述Table 1 Description of the datasets

3.2 评价指标

本文选取了两种被广泛使用的评估指标用于评估聚类的性能，即归一化互信息（normalized mutual information，NMI）［1］和调整后的兰德指数（adjusted rand index，ARI）［27］。NMI 和ARI 的值越大，表示聚类结果越好。NMI 可以有效地度量测试聚类和真值聚类之间的匹配度。设π′为预测标签，πG为真实标签。

π′和πG的NMI定义如下［1］：

式中：n′是π′中的簇数；nG是πG中的簇数；n′i是π′中第i个簇中的对象数量；是πG中第j个簇中的对象数量；nij是π′中第i个簇和πG中第j个簇所共有的对象数量；n是数据集的样本数。

ARI 是兰德指数（RI）［28］的推广，可衡量预测标签和真实标签之间的一致性。π′和πG的ARI计算如下［27］：

式中：N11是在π′和πG中属于同一簇的对象对的数量；N00是在π′和πG中属于不同簇的对象对的数量；N10是在π′中属于同一簇但在πG中属于不同簇的对象对的数量；N01是属于π′中不同簇但属于πG中相同簇的对象对的数量。

3.3 实验设计

为了系统地研究和比较不同聚类数对聚类集成最终结果的影响，将簇个数k 设置为：（1）k=k*，其中k*是数据集中包含的真实类别数；（2）在指定的范围内随机选择：［2，2k*］，［2，4k*］，［2，，［k*］。本实验中，K-means 算法运行20次，每次随机选取初始质心，获得20 个聚类成员作为1组，生成10组聚类成员集合。使用Ward算法对这10组聚类成员集合分别进行聚类集成，得到10 组聚类集成结果，并计算它们的NMI 和ARI，取平均值作为最终NMI和ARI。

3.4 实验结果

不同簇个数选择方法获得的聚类集成结果的NMI 和ARI 分别如表2 和表3 所示。由表2 和表3可见：

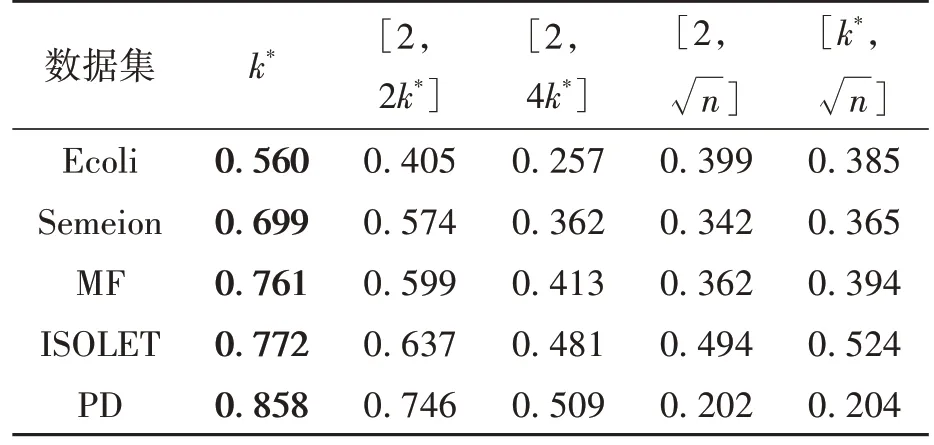
表2 不同簇个数选择方法获得的NMITable 2 NMI obtained by different cluster number selection methods

表3 不同簇个数选择方法获得的ARITable 3 NMI obtained by different cluster number selection methods

（1）当簇个数k = k*时，在所有数据集上都获得了最高的NMI和ARI。

（2）当簇个数k∈［2，2k*］时，聚类集成结果的NMI和ARI仅次于k = k*时的情况。

（3）由于不同数据集的k 和n 不同，所以［2，4k*］、［2］和［k*，］的值区间大小也不同，总体来看，这三种方法获得的聚类集成结果NMI 和ARI较低。

（4）在［2，4k*］和［2，］两种设置方法中，下限均为2，上限4k*与 n 的大小因数据集的不同而不同。MF 和PD 数据集的4k*小于，在［2，4k*］中的性能优于［2，］。Ecoli 和ISOLET 数据集的4k*大于，它们在［2，4k*］中的表现不如［2］。Semeion 数据集的4k*和大小接近，性能也相差无几。对于［2］和［k*，］，两组的取值上限相同，由于下限2 和k*的差异不大，所以两组的结果也很接近。一般情况下，选择区间为［k*］时，聚类集成效果较好。

综上，当选择的簇个数k 等于数据集的真实类别数时，聚类集成效果最好，随着簇个数选择的区间变大，聚类集成效果变差。

3.5 进一步探索

为了探究聚类成员簇个数选择的较优方法，本文缩小簇个数的取值范围，选择了［k*，1.1k*］， ［k*，1.2k*］，［k*，1.4k*］，［k*，1.6k*］，［k*，1.8k*］，［k*，2k*］这6 种设置方法（取值的上限向上取整），与k = k*进行比较。实验流程与之前相同，使用Ward算法进行聚类集成，得到的聚类结果NMI和ARI分别如图2和图3所示。由图2和图3可见：

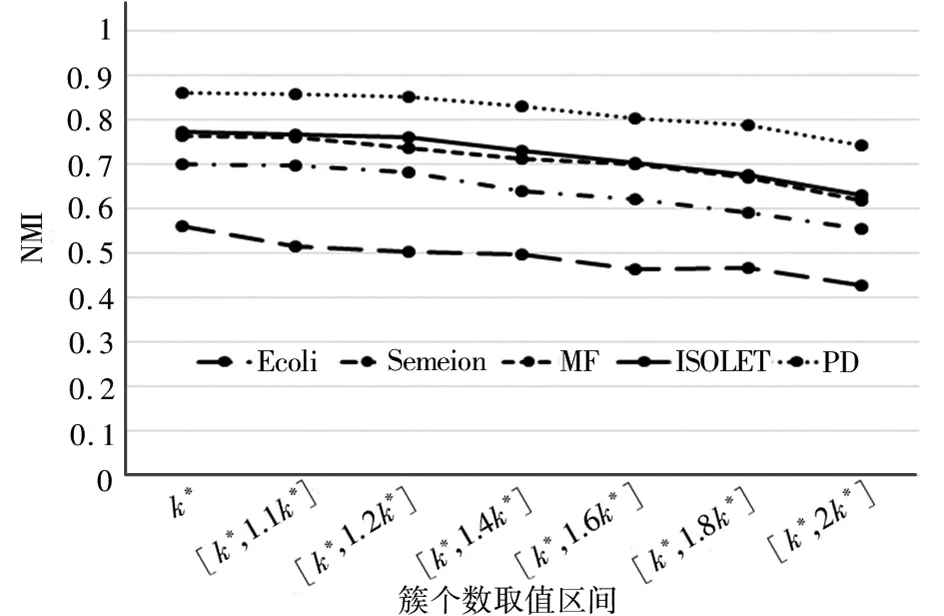
图2 取值区间较小时的NMIFig. 2 NMI with small value range

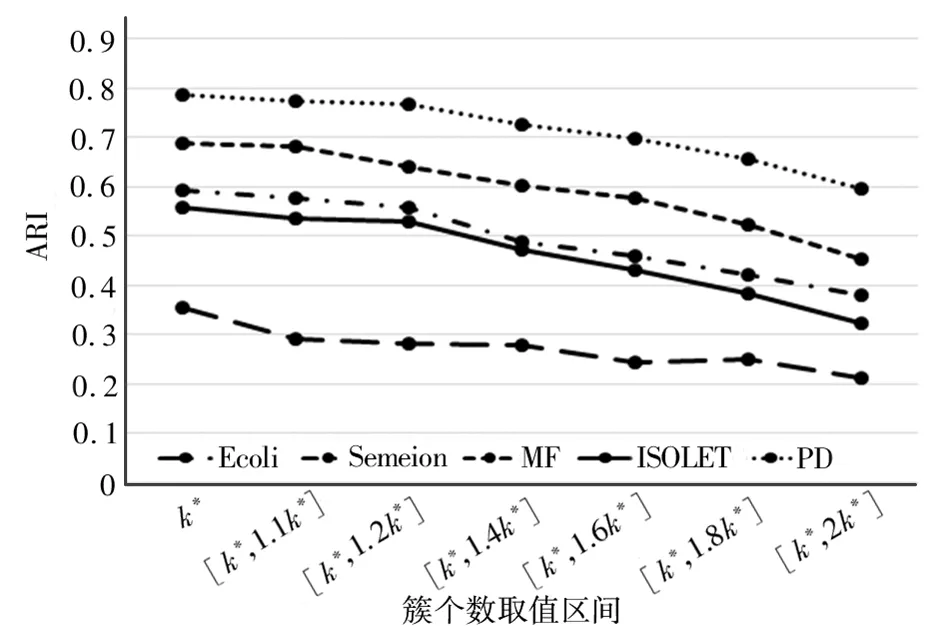
图3 取值区间较小时的ARIFig. 3 ARI with small value range

（1）当簇个数k = k*时，在所有数据集上都获得了最高的NMI和ARI；

（2）当簇个数取值区间增大时，聚类集成结果的NMI和ARI都在减小。

4 总结

本文系统研究比较了聚类集成中几种常见的簇个数设置方法，并进一步探索较优的设置方法。通过聚类集成效果的对比分析发现，将簇个数设置为真实类别数时，聚类成员的质量相对较高，能够获得较优的聚类集成结果。同时也发现当簇个数取值区间变大时，聚类集成效果变差。本文对不同的簇个数设置方法进行了比较研究，为聚类成员生成研究提供了有益的参考。