基于改进反演控制的食品分拣机器人末端执行器智能控制方法
韦树成 莫国志
(1. 广西机电职业技术学院, 广西 南宁 530007;2. 广西大学,广西 南宁 530000)
随着“中国制造2025”的到来,作为智能制造重要成员之一的工业机器人,近年来发展迅速[1]。同时,Delta并联机器人以其高速、惯性小等优点被广泛应用于食品等行业的高速分拣自动生产线[2]。相比于传统食品分拣方法,自动分拣具有效率高、误检率低等优点。
目前,国外众多学者对有关食品分拣机器人的控制方法进行了大量研究主要有PID控制[3]和滑模控制[4]等方法。柳振宇等[5]提出了一种改进的运动学闭环控制方法用于并行食品分拣机器人控制,与传统方法相比,位置跟踪误差降低了65%,轨道误差降低了50%。郝琳等[6]提出了一种改进的PID控制方法用于并联食品分拣机器人控制,与传统方法相比,该控制方法具有更高的抓取精度(99.9%)和稳定性。王敏等[7]提出了一种改进的粒子群优化算法用于并联食品分拣机器人控制,当输送速度为100 mm/s时,抓取成功率为100%,分拣效率为1.98个/s。毕宪东等[8]提出了一种新的动态目标抓取方法用于并行食品分拣机器人的抓取控制,与优化前相比,当输送速度为20 mm/s时,抓取速度从0.756个/s提高到0.860个/s;当输送速度为30 mm/s时,抓取速度从0.885个/s提高到1.130个/s。上述研究可以实现分拣机器人的智能控制,但上述方法难以实现准确、高效和稳定的位置跟踪,需进一步优化。研究拟提出一种将模糊系统(Fuzzy System,FS)、模糊神经网络(Fuzzy Neural Network,FNN)和反演控制算法(Backstepping Control Algorithm,BCA)相结合的并联食品分拣机器人智能控制方法,建模信息用FS逼近,未建模信息用FNN逼近和预测,BCA完成控制输出,并进行实验验证,旨在为并联食品分拣机器人的研究提供依据。
1 食品分拣机器人概述
并联食品分拣机器人由伺服电机、静平台、驱动臂、中间轴、动平台和从动臂组成(图1)。中间轴的作用是将动力传递给动平台,对末端执行器进行控制,从动臂为平行四边形结构,对动平台的自由度进行限制,动平台只能在空间上完成3个自由度的三维变换[9]。

1. 伺服电机 2. 静平台 3. 主动臂 4. 中间轴 5. 动平台 6. 从动臂
2 智能控制方法
2.1 并联食品分拣机器人动力学模型
并联食品分拣机器人动力学模型[10-11]:
MU**+CU*+KU+G+δd=τi-τf,
(1)
式中:
M、C、K、G——综合广义质量矩阵、衰减矩阵、刚度矩阵、重力矩阵;
U**——加速度,m/s2;
U*——速度,m/s;
U——位置坐标;
τi——广义输入矩阵;
τf——摩擦模型;
δd——干扰项。
机器人动力学模型具有以下特征[12-13]:
性质1:M是有界的,且
0<λmin(M)≤‖M‖≤λmax(M),
(2)
式中:
λmin(M)、λmax(M)——特征最小和最大值。
性质 2:CU*是有界的,且
0 (3) 式中: Cmin、Cmax——C的最小值和最大值。 性质3:M-2C为一个斜对称矩阵,且 (M-2C)+(M-2C)T=0。 (4) 性质4:G是有界的,且 ‖G‖≤Gg, (5) 式中: Gg——一个正常数。 2.2.1 反演控制 BCA的思想是将复杂非线性系统划分为多个子系统(不超过系统阶数), 对子系统Lyapunov 函数和虚拟控制变量进行设计,“反演”整个系统,直至完成控制律设计[9]。 BCA过程为: (1) 控制yo对期望角度yd进行跟踪。 定义误差z1[14]: z1=yo-yd。 (6) 设x2的估计为a1,误差z2为: z2=x2-a1。 (7) 在第一个子系统中,选择的李雅普诺夫函数为[15]: (8) 式中: λ1——Lagrange乘子。 如果z2=0,则第一个子系统稳定。 (2) 控制律为: (9) (10) τ1=-φ-λ2z2-z1, (11) 式中: τ——控制律; τ1、τ2——建模和未建模信息的控制律。 第二个子系统,选择 Lyapunov 函数[16]: (12) (13) 式中: d——外部干扰。 将式(11)代入式(13)[17],得 (14) 为方便控制,τ2满足 (15) 式中: χ1、χ2——逼近系数; FS的输出为[18] (16) 式中: θi——模糊隶属度函数达到最大值时的响应值。 (17) 式中: γ、κ——控制系数,且γ>0。 图2 FNN结构 由图2可知,FNN主要由输入层、隶属层、规则层和输出层组成[19]。输入为跟踪误差向量,输出为控制效应向量。 (2) 隶属层:隶属函数为高斯函数, (18) 式中: Npi——隶属函数个数。 (3) 规则层:输出是基于模糊推理机制给出的。 (19) 式中: lk——规则层的第i个输出,k=1,2,…,Ny; Ny——规则数。 (4) 输出层:输出为[20]: (20) 式中: o=1,2,…,No。 yo的矢量形式为 (21) 式中: No=n。 FNN的输入为z1∈Rn×1,输出为Ua∈Rn×1,实际控制量为 (22) 式中: ε——重构的最小误差向量; W·、m·、σ·——W、m与σ的最优值。 FNN-BCA输出控制量为 (23) 式中: W^、m^、σ^——W、m与σ的最优参数的估计。 定义逼近误差 (24) 式中: W~=W·-W^; L~=L·-L^。 利用泰勒级数展开,L~表示为[21]: (25) 式中: m~=m·-m^; σ~=σ·-σ^; m·、σ·——m与σ的最优参数; onv——高阶项矢量; m、σ——估计值。 qd、q分别为期望和实际驱动角,χ1、χ2为逼近系数,λ1、λ2为Lagrange乘子,η1、η2、η3、η4为学习率,γ为控制参数 为了验证试验所提控制方法的可行性和实用性,将该控制方法与自适应自抗扰控制ADRC[22]和自学习区间2型模糊神经网络自适应模糊滑模控制ST2FNNC[23]进行比较。控制目标是使并联食品分拣机器人的末端执行器准确、高效、稳定地跟踪期望轨迹。Delta机器人采用gts-400-pv系列运动控制器,交流伺服驱动器lexium23m,伺服电机bch1303m11f1c,减速器plx60-5,摄像机采用Basler aca2500-14gc。PC机采用Intel i5处理器、8 G内存、win10操作系统和Matlab 2018a作为仿真平台。试验参数见表1。FNN网络结构为2-20-25-2。控制参数γ=2、κ=1.5;学习率η1=0.4、η2=1、η3=1、η4=0.01。3个驱动关节为J1、J2和J3。 表1 试验参数 由表2可知,无论是瞬态驱动转矩还是稳态驱动转矩,试验控制方法的最大范围均小于ADRC控制方法和ST2FNNC控制方法。与ADRC控制方法相比,试验方法的最大瞬态和稳态驱动转矩在3个驱动关节处平均降低约2.8×104,4.6×104N·mm。与ST2FNNC控制方法相比,试验方法的瞬态和稳态最大驱动转矩在3个驱动关节上平均降低了3.0×104,1.5×104N·mm。综上,与传统控制方法相比,试验控制方法降低了对驱动元件的影响,有效改善了动态驱动特性。 表2 不同控制方法瞬态和稳态最大驱动力矩 由表3可知,与ADRC控制方法和ST2FNNC控制方法相比,试验控制方法有效降低了末端执行器在X、Y、Z方向的最大位置误差。与ADRC控制方法相比,试验方法末端执行器中心点在X、Y、Z方向的最大位置误差平均降低了0.44 mm;与ST2FNNC控制方法相比,试验方法末端执行器中心点在X、Y、Z方向的最大位置误差平均降低了0.43 mm,表明试验控制方法可以有效提高末端执行器的跟踪精度。 表3 不同控制方法的末端执行器中心点最大位置误差 为了尽可能接近实际操作条件,将相机的拍摄频率设置为100帧,传输速度为200 mm/s。罐头食品目标500个,以确保每次试验时传送带上的食品种类数量、分布密度、抓取速度等相同。 由表4可知,在相同的食品输送速度下,与ADRC控制方法和ST2FNNC控制方法相比,试验控制方法的抓取成功率最高。随着输送速度的增加,不同控制方法的抓取成功率在一定程度上降低,试验方法的抓取成功率从100%下降至99.60%,ADRC控制方法抓取成功率从94.00%下降至92.00%,ST2FNNC控制方法抓取成功率从99.00%下降至99.40%。 由表4还可知,当输送速度为100 mm/s时,相比于ADRC控制方法和ST2FNNC控制方法,试验控制方法具有最高的抓取效率,达到1.99个/s,比ADRC控制方法高18.45%,比ST2FNNC控制方法高3.11%。当输送速度为200 mm/s时,与ADRC控制方法和ST2FNNC控制方法相比,试验控制方法具有最高的抓取效率,达到1.94个/s,比ADRC控制方法提高了19.75%,比ST2FNNC控制方法提高了3.19%,说明试验控制方法具有较高的抓取成功率和效率。 表4 不同控制方法的抓取效果对比 综上,试验控制方法的控制性能明显优于ADRC控制方法和ST2FNNC控制方法,表明该控制方法可以有效提高末端执行器的跟踪精度,具有较高的抓取成功率和效率。 试验提出了一种将模糊系统、模糊神经网络和反演控制算法相结合用于并联食品分拣机器人末端执行器智能控制的方法。结果表明,相比于传统方法,试验方法具有更高的末端执行器跟踪精度和分拣效率。末端执行器误差小于0.30 mm,最大驱动扭矩小于4.0×104N·mm,当输送速度为100 mm/s时,分拣成功率和效率分别为100%和1.99个/s,当输送速度为200 mm/s时,分拣成功率和效率分别为99.6%和1.94个/s。然而,试验对并联食品分拣机器人末端执行器控制方法的研究仍处于初级阶段,在实际应用中存在许多影响因素,后期将不断完善。2.2 控制方法

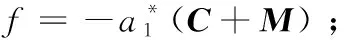


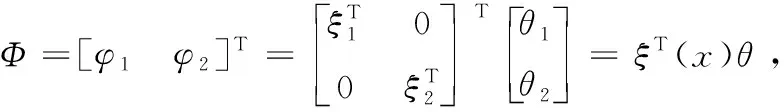
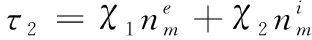

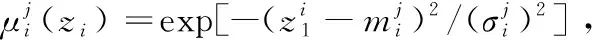
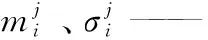
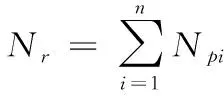

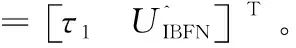

3 试验结果与分析
3.1 试验参数
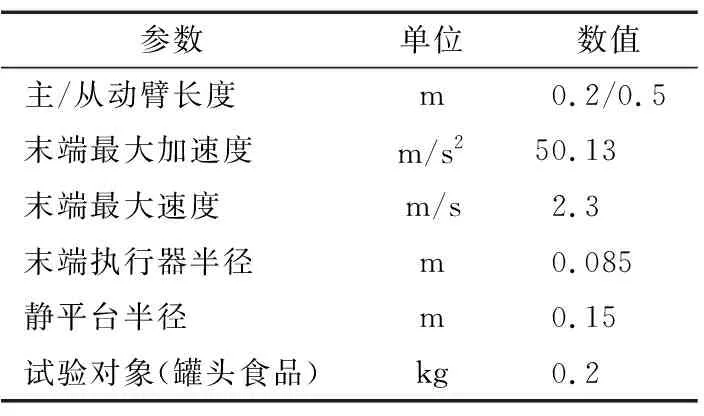
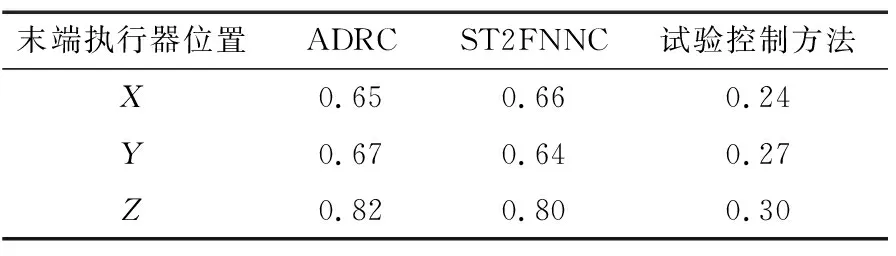
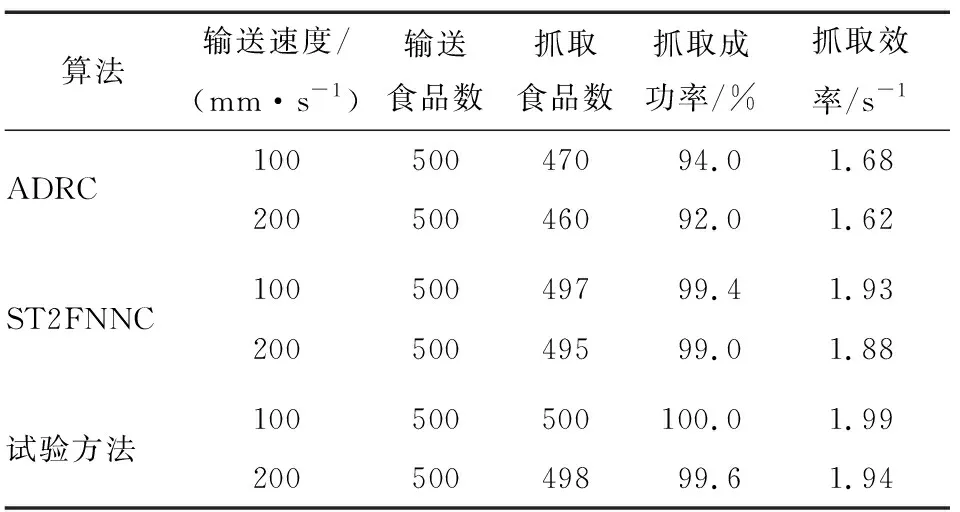
3.2 试验结果分析

4 结论

