改进遗传算法及其在矿山生产调度中的应用

王志文, 巩旭鹏, 孙洪涛, 胡绩强

(1. 兰州理工大学 电气工程与信息工程学院, 甘肃 兰州 730050; 2. 兰州理工大学 甘肃省工业控制先进控制重点实验室, 甘肃 兰州 730050; 3. 兰州理工大学 电气与控制工程国家级实验教学示范中心, 甘肃 兰州 730050; 4. 曲阜师范大学 工学院, 山东 曲阜 273100)

矿山开采作业是一个以采掘为中心、运输为纽带的大型生产系统.矿产资源是一种不可再生资源,近年来随着经济下行和矿产资源的逐渐枯竭,矿山必须采用高效节约的生产方式进行开采生产.信息化的不断发展,为矿山的智能化开采提供了支持,而生产调度在矿山的智能化中占据着重要的部分,它是资源合理利用的重要途径之一.

在矿山的生产调度中,主要使用采装和运输设备来完成.目前对矿山生产调度模型的求解主要有两种方式,其一是数学规划方法,主要由整数规划和动态规划等方法组成.这些方法存在一定的缺陷,如目标函数单一且对多约束问题模型求解困难,导致在实际应用中存在不足.而相较于数学方法,智能优化算法在求解相应的模型时优势明显.近年来,智能算法在矿山生产中应用极为广泛.Gilani等[1]介绍了露天矿长期生产计划(LTPP)的组合优化问题,以净现值(NPV)最大化为目标,在满足约束条件下采用启发式算法进行研究.在露天矿开采过程中,考虑矿山可达到的最大净现值来优化品位是露天矿开采的关键问题之一.Ahmadi等[2]采用两种不同的元启发式优化算法来确定最优品位.寻找露天矿生产调度问题的最优解是矿业界公认的具有挑战性的问题之一.Elsayed等[3]提出了一种基于差分进化的方法和修复机制,保证了算法的可行性,并结合局部搜索技术来提高算法的性能.Paithankar等[4]使用最大流量演算法与遗传演算法来产生长期的生产调度.在不确定条件下,建立了多时段最大流量的图结构,并用遗传算法控制弧内流量,以制定生产计划.刘文博等[5]根据实际生产过程特点,建立了规整性的开采调度问题模型,并结合拉格朗日松弛算法和启发式算法进行求解.

目前大多数的算法针对单一目标函数,算法的收敛性和准确性有待提高,且应用到矿山生产调度中不利于获得最优解,降低了开采效率.针对以上问题,本文提出一种改进的遗传算法,以采掘最小成本和矿山最小运输费用为目标,构建多目标生产模型,实现多出矿点协调生产调度的优化.

1 矿山多目标生产计划模型

露天矿的运输方式多种多样,主要包括卡车运输、轨道运输以及多种方式联合运输.卡车运输以其灵活性强等优点得到广泛应用，其整个运输过程是将每个铲位的矿石和岩石运送到相应的卸点.矿石的卸点有矿石漏和倒装场,岩石的卸点有岩石漏和岩场.

本文假设该矿区有8个出矿点,卡车将各出矿点的矿石和岩石运输到相应的卸点.定义其生产调度标准集合B={Dij,Nij,Mij},分别代表出矿点到卸点的距离、出矿点到卸点的最大运输次数、运输费用.卡车运输线路分布如图1所示.

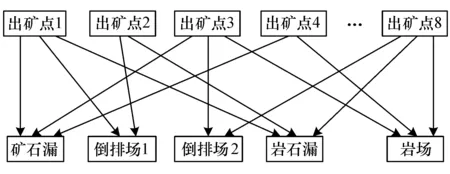
图1 卡车运输路线Fig.1 Truck transportation route

本文所建立的模型是以矿山的采掘成本和卡车的运输费用最小为目标,并对卸点矿石漏、倒排场1、倒排场2、岩石漏和岩场依次编号为1、2、3、4、5,建立数学模型如下：

(3)

其中：α+β=1,α、β为线性加权系数,根据实际情况确定其数值；C为卡车总费用;C1为卡车运输费用;C2为矿山生产成本；ci为出矿点i采掘成本；xi为第i个采点的出矿量；Xij为出矿点i到卸点j的卡车数量(单位：辆；i=1,2,…,8；j=1,2,…,5)；Dij为出矿点i到卸点j的距离(单位：千米；i=1,2,…,8；j=1,2,…,5)；Nij为出矿点i到卸点j的最大运输次数(i=1,2,…,8；j=1,2,…,5)；Mij为出矿点i到卸点j的费用(单位：元/千米·辆).

其中：n为出矿点个数;L为卡车的载重量,吨；pi为出矿点i的矿石质量分数;Pj为卸点j的需求量,吨；qi，min、qi，max分别为出矿点i的最低出矿量和最高出矿量.

2 遗传算法及其改进策略

遗传算法是一种基于生物自然选择与遗传机理的随机搜索与优化方法[6],在很多方面都有广泛的应用[7].但是该算法存在诸多不足,如算法参数要求高,收敛速度慢且容易陷入局部最优[8].

因此,许多学者研究改进标准遗传算法,以此来弥补算法存在的缺陷.仲兆满等[9]通过改变种群的规模来减少近亲的交配.Goldberg等[10]提出一种间接性交配策略避免近亲杂交.Strickberger和任芳等[11-12]根据表现型的相似与否来选择交配的对象,即选型交配这一策略避免近亲杂交.吉根林[13]将遗传算法与爬山算法相结合,提出自适应变异概率的优化算法.张超群等[14]提出动态参数编码,即动态地改变参变量的定义域,有更好的搜索范围来克服二进制编码带来的精度与效率不高,且过早收敛的问题.牛琳[15]针对柔性作业车间调度中遗传算法局部收敛的问题,结合柔性作业车间调度的特点,采用模拟退火算法融合遗传算法对调度领域进行了研究.杨进帅等[16]通过定义多目标规划的非隶属度,调节控制参数来增强局部搜索能力,指导个体寻找最优值.

本文首先给出近亲度的判别式,在此基础上引入异种机制,避免了父代之间的近亲杂交,得到更优良的子代.

2.1 基于禁止近亲杂交的算法

在基因进行交叉过程中,标准遗传算法的交叉概率一般为给定的,这忽略了个体之间的相似度,并使得父代的优秀基因遭到破坏,导致算法不能收敛或出现局部收敛的情况.为了解决该问题,本文在此引入近亲度的概念,提出一种禁止近亲杂交的自适应遗传算法(adaptive genetic algorithm,AGA).

在遗传算法的后期,近亲个体间的杂交会导致种群多样性的破坏,进而使算法收敛速率降低甚至不能收敛.因此本文引入近亲度这一概念,并给出了判断相似度的函数和阈值.根据这一标准对双亲进行筛选,如若超出阈值,则强行淘汰其中一方,重新选择配对方[17].相似度定义如下：

定义其在n维空间中的距离为

(9)

(10)

如果p(T)大于算法给定的近亲繁殖判据pb,则认为第T代种群发生了近亲繁殖.即近亲繁殖的判别式为

(11)

相似度能够更直观地反应个体之间的差异,为了明确这种差异是否需要进行变异,可引入交叉临界值.如果相似度值小于该值,则说明将要杂交的个体为近亲,继而重新选择交叉的个体,这样就避免了由于近亲杂交而产生不良个体,保证遗传操作的正常进行.

2.2 最优保持策略

在遗传优化过程中,理论上来说遗传算子和选择机制可以使子代的平均适应度高于父代.但由于遗传算法的不确定性,子代中的最优个体并不总是优于父代中的最优个体.为提高优化效率,保证算法能够更加精确地收敛于全局最优解,本文引入了最优保持策略.具体的操作方法是在选择的过程中,允许父代和子代竞争,使适应度较高的个体具有较大的生存概率,确保能够进入下一次循环继续参加遗传优化过程.

最优保持策略的作用是显而易见的.根据遗传算法的模式定理,采用最优保持策略的简单遗传算法可以概率收敛于全局最优解,而不采用最优保持策略的简单遗传算法则不能以概率收敛于全局最优解.由此可见最优保持策略的重要性.

2.3 异种机制

变异算子在遗传算法中是一个很重要的因素.如果变异概率选择过大,则会破坏算法的稳定性；如果选择过小,则会影响种群多样性的保持.

事实上,自适应随机变异的实质都是根据从优化过程中反馈回来的适应度函数信息,不断缩小搜索范围,进而求得最优解.这有利于算法的迅速收敛,但也增大了近亲繁殖的概率.为解决这一问题,本文探索性地提出了异种机制以防止早熟收敛,提高收敛效率.

异种机制即是在遗传优化过程中扩大其搜索范围,选择搜索范围之外的种子进入到算法中,进而增加种群的多样性.它模拟的是人工干预物种进化,获取优良物种的过程.其作用机理是：

1) 对遗传优化过程进行监控,若发生了近亲繁殖,则启动异种机制；

2) 在缩小了的搜索范围之外选择数个异种,用以代替现有种群中适应度较低的个体；

3) 将加入异种的现有种群生成子代,再进行下一次循环.

2.4 异种的选取

异种的选取方法有两种：一种是不考虑近亲繁殖本身的特点,在近亲繁殖个体所在的邻域内完全随机地选择；另一种则是考虑近亲繁殖发生的特点,根据近亲繁殖的趋势选择异种的方法.

(12)

随机选取异种的方法与变异操作相类似,即：

(13)

其中：τ是在[-1,1]上取值的随机数；bh是异种机制的最大突变半径.

为使异种的选取具备自适应变焦的能力,可将bh取为当前繁殖代数T的函数：

(14)

其中:bhs、bhl是第k个设计变量在遗传优化过程中选取异种的上界和下界.

用这种方法得到的异种是：

(15)

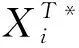
2.5 终止条件

GA算法的终止条件也是极为重要的一个因素.在算法收敛问题的判断上,已有很深入的研究.Brest等[18]预先给定收敛代数来判断终止与否；Pan和Zhang等[19-20]首先给定适应度值,再依设定的阈值判断适应度值之间的差异是否达到收敛标准.尽管这些标准都较为简单,易于操作,但是机械化比较严重,并不能根据实时情况作出判断.

随着演化的进行,个体间的差异越来越小,所以近亲度也成为一个重要的因素.

本文提出一种新的终止条件,即将近亲度和种群聚集度相结合,这种方法具有自适应性.本文中指标满足以下两个条件时,算法终止.

1) 种群聚集度：种群间的距离和适应度之间的距离都在0.1%以内；

2) 近亲度p(T)：p(T)>99%.

算法流程如图2所示.

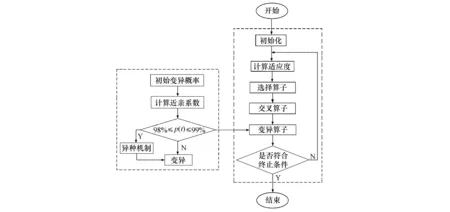
图2 AGA算法流程Fig.2 AGA algorithm flow

2.6 算法结果测试

本文选择精英策略、轮盘赌选择和二进制编码,所有的测试函数都被计算200次,设置种群规模为20.当近亲度大于设定阈值时,禁止近亲策略开始起作用.为了进一步验证改进算法,利用多个测试函数(见表1)主要比较全局收敛率、平均收敛代数、寻找到最优值的平均值及其方差.

表1 测量函数

标准遗传算法(SGA)和改进自适应遗传算法(AGA)的性能比较如表2所列.可以看出,虽然种群规模较小,但是通过禁止近亲策略改进的AGA算法的收敛率有明显提高.AGA算法计算出最优值的平均值,更加接近最优理论值,最优值的方差也明显减小.说明改进的算法提高了算法的全局收敛率,在避免早熟方面起到了重要作用.

表2 数值计算结果

3 用遗传算法求解调度模型

在采用染色体设计相应的卡车数量时,首先将染色体进行初始化编码,再依据本文提到的近亲度判别式进行判断,如若种群没有发生近亲繁殖,则直接进行解码,得到调度方案；否则应采用异种机制,避免近亲繁殖,使其调度方案更接近实际要求.

3.1 染色体编码

本文采用二进制编码方式,假设出矿点与卸点之间的卡车数量在8辆以内,对Xi1、Xi2、Xi3、Xi4、Xi5进行编码,则只需3位二进制就可以表示所有的卡车数,编码如表3所列.

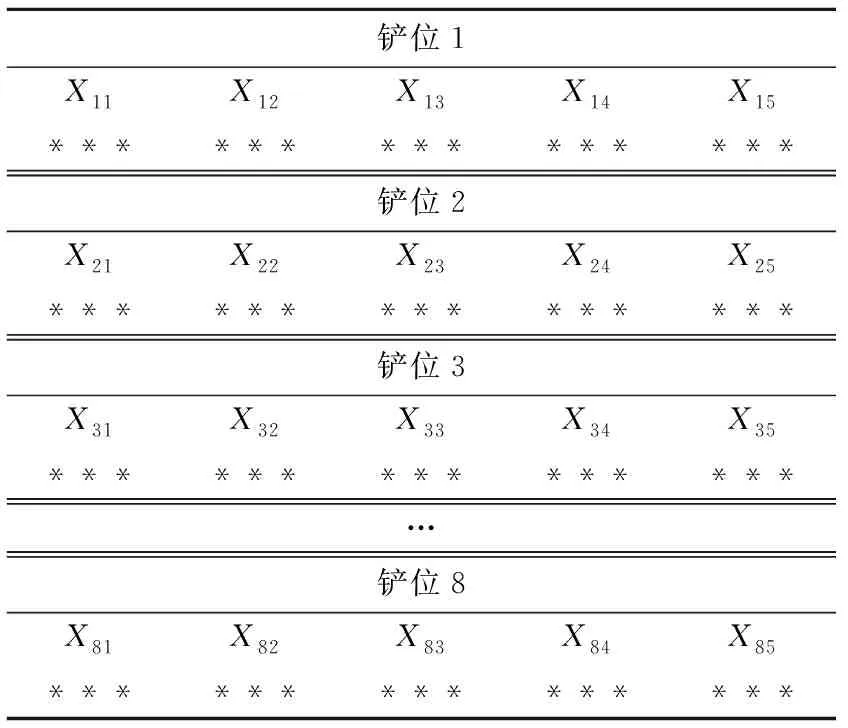
表3 编码格式

露天矿中的出矿点由第一行表示,第二行代表各出矿点对应的卸点,第三行代表0-1变量.当出矿点到卸点有卡车运行时,其3位二进制编码不为零,否则为零.如出矿点1到倒排场2被安排了5辆车,则Xi3对应编码为101.所显示的不同的编码代表不同的调度方式.

3.2 近亲度判断

3.3 染色体解码

运用遗传算法将卡车调度进行优化得到最优解,并转换基因型为表现型.经过遗传操作,将得到的最优染色体进行解码.首先对染色体从左到右每3位进行分组,得到卡车数量.再将得到的10个分组每5个分为一组,则每一组代表一个出矿点,即得到两个出矿点.每个3位二进制数转化成十进制数,即得到出矿点到卸点的卡车数量，如表4所列.

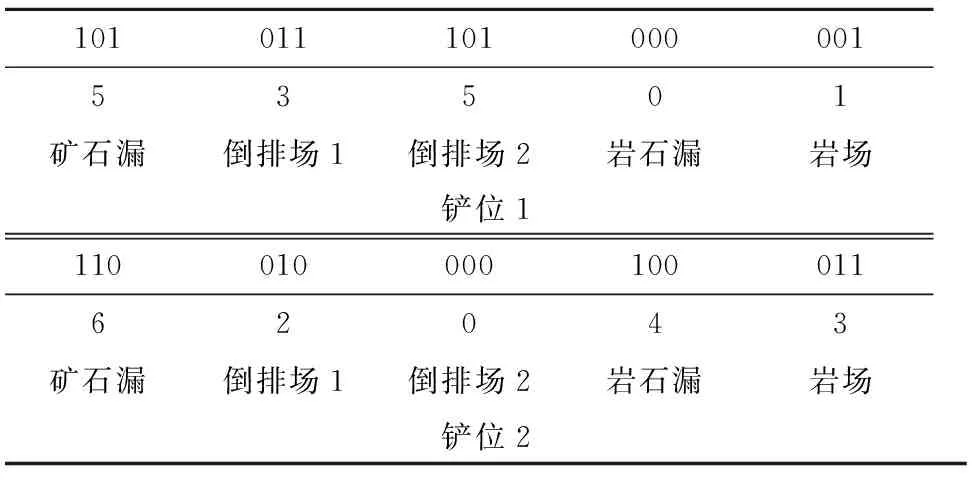
表4 染色体解码

由表4中染色体可看出,铲位1到矿石漏、倒排场1、倒排场2、岩场分派的卡车数量分别为5、3、5、1,到岩石漏没有分派车辆.铲位2到矿石漏、倒排场1、岩石漏和岩场分派的车辆数,分别为6、2、4、3,到倒排场2没有分派车辆.即可得到一种调度方案.

4 实验仿真与结果分析

4.1 各铲位出矿量优化

已知该矿区有8个出矿点,各铲位矿石产量、矿石品位及其采掘成本如表5所列.算法参数设置与前文一致.在出矿生产中,出矿量指标为1.5≤xi≤8(万吨).将遗传算法优化前后各出矿点的出矿量进行对比,如图3所示.优化后得到的出矿量为x=(6.34,4.26,5.04,4.05,3.56,2.82,5.32,2.98),出矿点总产量为34.37万吨,相比于计划产量28.42万吨,优化算法后得到的产量有显著提高.

表5 各铲位矿石产量和矿石品位

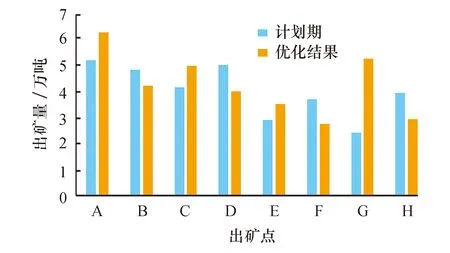
图3 各出矿点出矿量优化前后对比Fig.3 Comparison before and after the optimization of ore drawing amount at each ore drawing point

4.2 目标函数优化

采用改进遗传算法及其标准遗传算法对目标函数进行优化,经过各代的逐次运算,分别得到两种算法的求解迭代曲线,如图4所示.各出矿点到卸点的距离、最大车辆数即车次数据如表6和表7所列.

表6 各铲位到各卸点之间的距离

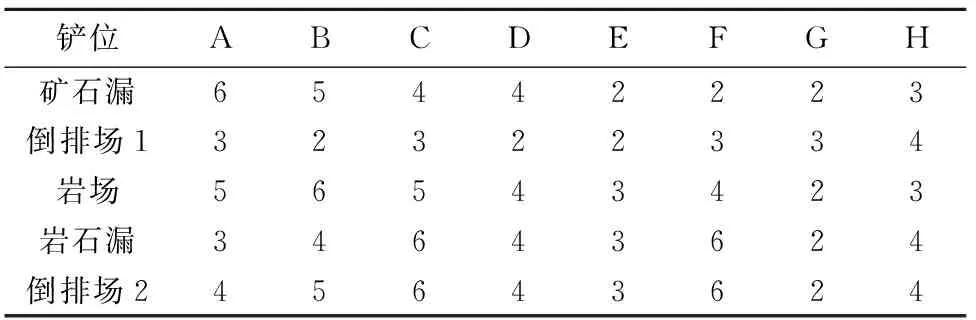
表7 各铲位到各卸点之间的车次

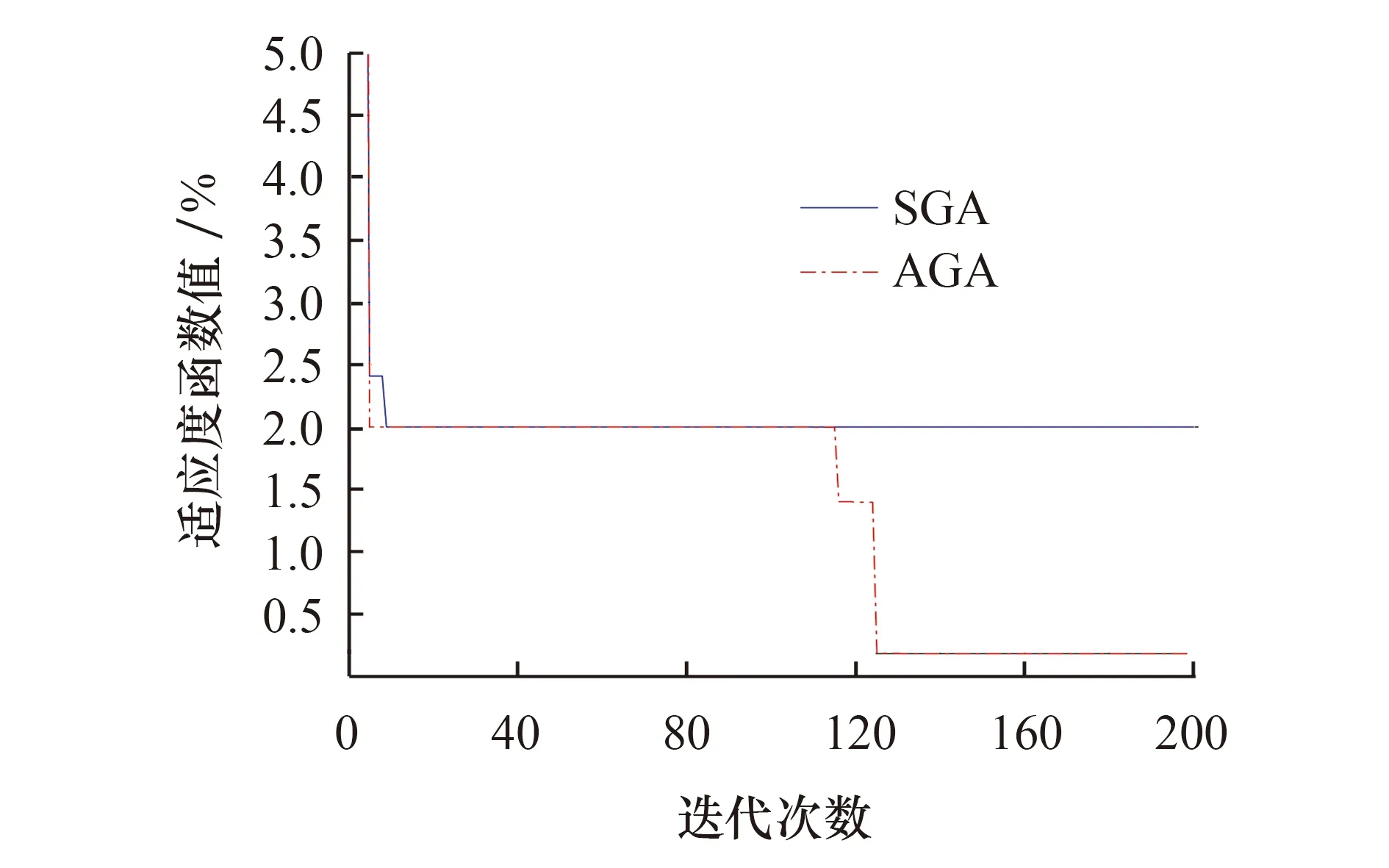
图4 最优适应度值Fig.4 Optimal fitness value

由图4可以看出，在遗传算法的初始阶段，迭代次数在10左右时，适应度值曲线变动较大，很快得到改善.在以后的各代中，AGA算法在120～130代之间开始趋于平稳，验证了所改进算法在解决矿山开采问题上的可行性；SGA算法在寻优过程中会陷入局部最优，而AGA算法相对于SGA算法有更好的寻优结果,更符合所期望的目标值.此外,在收敛时间方面,优化后的算法消耗时间更短.进一步验证了所提改进算法的优越性.

5 结论

本文综合考虑实际矿山生产调度相关要素,以卡车运输和矿山开采成本最小为目标函数,考虑矿石品位等约束条件,构建多目标生产调度模型,提高矿山资源的合理利用.此外,本文提出的改进算法具有较强的自适应搜索和避免近亲杂交的能力,保证了后代的优良基因,增加了种群多样性,改善了经典遗传算法的早熟停滞现象.为进一步验证改进算法,利用多个经典函数测试其算法性能,结果显示改进算法的性能有了明显提高.结合该改进算法对矿山生产调度进行深入分析,验证了改进算法在该问题上的优越性.最后依据矿山生产作业数据进行仿真实验,得到的各铲位的出矿量和采掘、运输成本更符合矿山开采需求.

本文只在确定性条件下分析了矿山的生产调度,在以后的研究中,应将不确定因素考虑进来,实现生产调度对随机因素的实时管控.

致谢：本文得到甘肃省工业控制先进控制重点实验室开放基金(2019KFJJ03)项目的资助，在此表示感谢.