基于改进小波阈值的GIS局放监测抗干扰研究

许 星，赵巧娥，吕 高，刘 伟

（山西大学 电力与建筑学院，太原030013）

随着我国电力系统的高压输电工程的发展，GIS 凭借着自身特有的优势，得到了广泛的实际应用。在GIS 现场运行过程中，难免会发生各种各样的故障，大致有以下几类：绝缘故障、机械故障、线路故障等。据统计，设备的绝缘体长期工作在高温、高压等环境下，引起的绝缘故障占总体故障80%左右，而局部放电是影响设备发生绝缘的重要因素，同时也是设备绝缘状态的重要表征，局放的长期存在会引起设备绝缘强度降低甚至失效[1-2]，从而引发电力击穿等情况，造成停电事故，使系统瘫痪，对人民的生活造成不好的影响。因此，需要对GIS 的局放信号进行监测，从而来保证高压及特高压等电气设备的安全运行。

在GIS 内部发生局放时，它的击穿过程极快，会产生陡峭的脉冲电流，激发高频率的电磁波。故可用特高频传感器检测GIS 内部局放电流产生的电磁波信号，从而判断设备的缺陷状况，其优点是可避免大量低频噪声信号的干扰。然而设备在现场运行环境中，还会存在由于电气设备工作而产生的白噪声，它们会极大的干扰采集到的局放信号，有的局放信号可能会被这些噪声湮没，或者使信号发生畸变，对局放智能监测设备的准确性带来了严重的影响，导致不能及时发现GIS 内部的缺陷，影响工作人员判断GIS 内部是否发生故障。因此，有效地抑制噪声干扰，同时提取超高频局放信号中的有效特征量成为如今研究热点之一[3-4]，从而来保证对局放信号进行精确的分析，进一步判断设备的运行状况，为工作人员制定合理的检修计划提供参考。

局放信号是具有非平稳特征的时变信号，通常在时域上表现为指数衰减函数或高斯函数的形式，需要采用合适的时频分析方法对其进行去噪处理。文献[5]指出小波函数可以寻找最优函数来抑制局部放电混频随机窄带噪声。小波分析[6-7]在特高频局放信号去噪方面得到了广泛应用。文献[8]提出了峭度值对信号中的冲击成分敏感，常用作表征信号脉冲与震动。多尺度小波变换可以把信号分解为多个尺度空间[9]，该方法适合非稳态、高频以及暂态信号的去噪[10]。GIS 特高频局放信号上升时间极短，数量级很小[11]，是典型的高频非稳态信号，因此小波分解可用于GIS局放信号降噪处理。基于上述的分析，本文对于GIS 内部产生缺陷时所仿真的局放信号含有各种噪声干扰问题，提出基于改进的小波阈值的算法对局放信号进行去噪处理。

1 小波阈值去噪

小波阈值去噪主要包括3 个步骤：

（1）选取合适的小波母函数，确定其分解的层数，对信号进行分解；

（2）选取恰当的阈值，采用阈值函数对小波系数进行阈值处理；

（3）根据阈值处理后的小波系数，经小波逆变换，对其进行信号重构，实现去噪的效果。

在实际应用中，对于阈值函数的选取则决定了去噪效果的好坏程度，因此选取合适的阈值函数相当重要，一般通用的方法为硬阈值及软阈值，硬阈值处理是当小波系数大于阈值时不变，相反则为0。可表示为

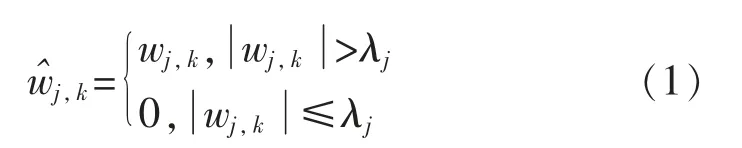
软阈值处理是小波系数大于阈值时，朝幅值减小的方向收缩，相反小于阈值则为0，可表示为

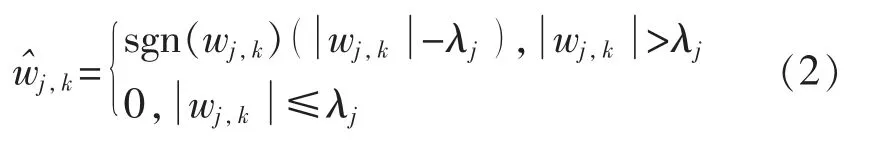
其中：

式中：λj为阈值；wj，k为分解系数；为预估小波系数。

2 改进阈值函数的小波熵

2.1 小波熵

小波熵就是通过小波分解得出的系数矩阵，处理成一个概率分布序列，其计算得到的熵值，能表示矩阵的稀疏程度，可用它抑制信号的无关成分，其计算流程如图1所示。流程如下：

图1 小波熵计算流程Fig.1 Flow chart of wavelet entropy calculation

不同分解尺度的高频信息量作为独立信号源，将各层高频系数分为n个等长小区间，计算各区间的小波熵。设第j层高频系数为dj，N为采样点，第k个子区间熵值为

计算出小波熵值后，进而比较各子区间的小波熵值，选择小波熵值最大的子区间的小波系数估计噪声方差。本文采用修正的阈值计算公式，可表示为

式中：m为调节系数。

2.2 改进阈值函数

小波变换的分解与重构是采用滤波器函数，把分解信号分为低频系数及高频系数，再采取而抽取获得小波系数。设计的滤波器组可以对信号进行重构，但在二抽取的过程中仍存在部分缺陷，使得信号发生混叠，造成信号畸变，对原始信号的小波系数产生了较大影响。同时，常用的硬、软阈值算法在实际的应用中有较好的效果，但它们各自都有一定的局限性，硬阈值方法就是小波分解系数小于阈值时为0，高于阈值全部不变，此方法可以使信号边缘的局部特性很好的保留下来，但与软阈值处理方法对比后可发现，该方法处理后的信号显得十分粗糙，产生此现象的原因是硬阈值处理方法在正负阈值处不具有连续性，导致信号的结果有较大的方差，系统出现震荡现象。软阈值方法是当分解系数大于阈值时减掉阈值，它是连续函数，因此信号的平滑性相对硬阈值而言要好些，但同时也使分解系数与预估系数之间产生了恒定的偏差，对重构后的信号准确性有极大的影响。为了使分解系数与预估系数之间的偏差对重构信号的影响降低，本文通过对硬软阈值进行改进，重新对阈值函数进行构造，如式（5）所示：

式中：Cj，k为加入干扰噪声后的小波系数；是预估的小波系数；λ 是调节系数；λj是阈值。

对于软阈值函数来说，由于噪声干扰后的小波系数和预估出的小波系数的绝对值有差值λi，使重构后的信号准确度偏低，因此需要减小它们之间的差值对结果带来的影响。而硬阈值函数干扰后的小波系数与预估的小波系数间没有差值，并且不连续，重构后的信号也不理想。通过分析局放信号与干扰噪声在小波空间的分布规律可知，局部放电信号的信息大部分都聚集在高尺度上，而干扰噪声主要是在低尺度上，可考虑在高尺度上采用近似硬阈值的算法尽可能降低局放信号能量的损失，在低尺度上运用近似软阈值的算法保证提取信号的平滑度，可以通过这种思想来对传统的阈值函数重新构造，重新构造的阈值函数与传统的阈值函数对比后发现，该函数有高阶导数，在初始信号与噪声信号间有平滑的过渡区间。考察重构后的阈值函数：

（2）判断其连续性，由于函数为奇函数，故只需分析坐标轴的右半部分即可。由于该函数为分段函数，因此需要判断函数在阈值λj处的连续性，由定义得：f+（λj）=f-（λj）=0，故函数在阈值处连续。证明函数连续是为了改善函数不连续引起的信号重构振荡现象。

（3）当x→+∞时，f（x）→x，随着小波分解系数Cj，k变大，软阈值方法的与Cj，k间的偏差会减小，从而使信号重构的精度提高，噪声对信号干扰得到了有效地抑制。

2.3 改进阈值函数的小波熵步骤

通过小波熵来确定阈值大小，结合改进阈值函数，采用改进阈值函数的小波熵方法，计算流程如图2所示。具体的流程如下：

图2 计算流程Fig.2 Calculation flow chart

（1）通过小波分解加噪的局放信号。选取小波基，确定分解的尺度j，将信号分解到层，得出不同尺度下的高频系数及低频系数；

（2）计算不同尺度高频小波系数的熵值。将1-j层区间划分为n份，通过式（3）得出不同层下各个子区间的熵值；

（3）计算不同尺度小波系数阈值。在每一层选择最大熵值子区间的分解系数，计算此区间小波系数的中值，它是该层的噪声方差，再根据式（4）计算每个层的阈值；

（4）对不同尺度高频小波系数通过阈值处理。对各层高频系数按式（5）重构的函数进行处理，得到不同尺度下每个层的高频小波系数；

（5）根据最高层的低频分量，采用阈值处理后每一层的高频分量，将其重构进而得到去噪后的信号。

（1）判断其奇偶性，由定义知，f（-x）=-f（x），定义域为实数，确定此函数为奇函数，和传统的硬软阈值函数无差别。

3 仿真分析

3.1 数学模型建立

GIS 内部常见的绝缘故障有4 种，由于放电机理不同，故产生的局放信号形状及特征也会不同，国内外的学者采用耦合电容法构造4 种数学模型，但此类方法产生的信号频率较低，与特高频信号相比，略有不足之处，不适合特高频局放信号的模拟仿真，因此本文通过建立GIS局放特高频局放信号的数学模型，来模拟金属突起导致的尖端放电产生的超高频局放信号：

式中：N为局放信号的极值数，一般情况取3～5，本文取N=4；Li为局放信号波峰的高度；xi为局放信号波峰所对应的横坐标值；di为局放信号波峰的陡峭程度。

3.2 仿真

仿真出原始的超高频局放信号波形如图3所示，然而在GIS局放信号的现场检测过程中，会存在各种干扰，不容易获得原始的局放信号。为了尽可能的模拟现场环境，加入信噪比为-10 dB 的白噪声对模拟的信号进行干扰，加噪后的模拟信号波形如图4所示，当噪声对信号干扰较大时，原始信号被完全覆盖。

图3 原始信号Fig.3 Original signal

图4 加噪信号Fig.4 Add noise signal

为了验证文中改进的去噪算法的优势，本文对比硬软阈值及改进阈值方法的去噪效果，波形如图5、图6 和图7所示。

图5 硬阈值去噪Fig.5 Hard threshold denoising

图6 软阈值去噪Fig.6 Soft threshold denoising

图7 改进阈值去噪Fig.7 Improved threshold denoising

为了对各类算法的去噪效果进行评价分析，采用信噪比、均方误差来客观的评价去噪效果，信噪比表达式为

均方误差表达式为

式中：x（i）为原始信号；y（i）为处理后的局放信号；N为信号采样的个数。计算结果如表1所示。

表1 计算结果比较Tab.1 Comparison of calculation results

由表1 可知，相比于传统的硬软阈值算法，本文提出的改进算法去噪的信噪比更高，并且均方误差也更小，因此具有更好的去噪效果。

3.3 仿真结果分析

从图7 中可以看出，本文提出的改进算法相比较传统的硬阈值算法而言，硬阈值处理后信号还是会有大量的干扰，仍旧不能分析出GIS局放信号出现的位置。由于函数不连续性而造成的波形畸变率较高得以解决，信号更加平滑，相对于软阈值而言，改进算法的幅值要比软阈值算法高，产生此现象的原始是软阈值处理信号显得过于平滑，削弱了原始信号的能量，导致局放信号失真。改进后的算法则减少了预估小波系数和小波分解系数间存在差值的影响，同时，改进算法中结合小波熵值，使微小且急促的异常信号得以抑制，处理后的波形和原始信号较为相近，可以较清晰的分析出GIS局放信号出现的位置，使GIS 监测的效率进一步提高。

4 结语

对于传统小波存在的问题，本文提出了一种结合小波熵值的改进阈值函数对局放信号进行去噪。仿真结果表明，与传统的算法相比，本文提出的改进方法提高了信噪比，同时均方误差更小，使异常的信号得到抑制，效果更好，更为接近原始的局放信号，方便工作人员对局放信号进行精确的分析，准确的分辨出局放信号发生的位置，及时做出预防，提高GIS局放智能监测的效率。