基于LSTM的地基微波辐射计湿度廓线反演
周高进 杨智鹏,2* 彭静 杨玲 陶法 茆佳佳
(1 成都信息工程大学电子工程学院,成都 610000;2 中国气象局云雾物理环境重点开放实验室,北京 100088;3 中国气象局气象探测中心,北京 100081)
引言
水汽在大气中仅占1%~3%,却是大气中最多变且最重要的成分[1]。大气湿度廓线能够很好地反映水汽在大气中的分布,在进行天气系统的预报,气候的研究和预测中发挥着十分关键的作用[2]。自1749年英国人开始尝试用风筝进行底层大气温度的测量,至1927年逐步发展起来用于业务观测的无线电探空仪[3]。在日常观测中,主要可以从全球探空仪网络获得大气湿度的垂直剖面图[4]。虽然其测量的数据准确,但是由于观测结果受到其成本和时间分辨率(主要是每天一次或两次)的限制,不足以捕获大气结构的变化[5]。为了解决这一问题,研究人员探索发现地基微波辐射计(Microwave Radiometer, MWR)可以提供高时间分辨率的数据,并且对环境适应能力强,十分适合于自动全天候观测[6-8]。
基于地基微波辐射计有着连续观测的特性,能够反演获得不同高度层的温度[9]和湿度[10], MWR已广泛应用于大气廓线反演工作当中[11-13]。MWR主要通过反演的方法把获取到的亮温数据计算出大气温湿度廓线数据。随着气象领域的进一步发展,多种数学方法也同样被引入到其中,并且相继提出了多种反演方法,其中包含一维变分(1D-VAR)反演方法、非线性回归法[14-16]、多元线性回归算法[17-18]、Bayesmn最大概率估计法[19]、蒙特卡罗法[20]、神经网络方法[21-23]等。其中,神经网络反演方法已经充分地证明了其优点,Cimini等[24]将多种反演算法进行了比较, 提出神经网络法对于大气廓线反演这种非线性问题有着更好的表现。在现有基于神经网络方法进行温湿度廓线的反演中普遍所使用的方法为反向神经网络方法(BP)[25-27]。
然而,这些使用BP神经网络的方法获取的精度还存在一些不足,造成业务使用不够普及。首先,现有研究使用网络结果过于简单,BP模型仅仅属于浅层模型,其随机初始化会令训练陷入局部最小值,并且在数据量比较大时耗时过长。另一方面使用单层隐藏层会使得BP算法不够精准,而增加隐藏层又往往会引起梯度弥散的问题。另外,BP网络通常采用的是sigmoid或者tansig激活函数,但是K. Wang等(2017)提出这些常见的非线性的激活函数经常会使得在进行训练的过程中出现梯度爆炸和梯度消失的问题。目前,结构网络更复杂的循环神经网络(Recurrent Neural Network,RNN)已经开始逐步应用于回归问题当中[28]。该方法与同传统的神经网络相比,最显著的特点是加入了探测仪器在一段时间的探测数据,包含了探测数据随时间变化的信息,且其隐藏的神经元间能够进行信息传递,从连续观测数据中建模学习,从而提高反演精度。
另外,使用BP神经网络方法进行反演晴空情况下的湿度廓线已经有了一定的应用[29],但进行反演非晴空情况下的湿度廓线效果仍然较差。尽管MWR的红外传感器能够探测云底的高度,但其对云底以上的信息测量能力较差[30]。为了提升有云情况下的大气湿度廓线反演能力,研究人员把其他设备观测的云信息添加进廓线反演训练中[31]。毫米波云雷达能够连续观测有云条件下的云信息,包括云量、云层厚度、云的大小等,能够有效地提高MWR在有云条件下的反演精度[32]。并且,已有研究证明,把云雷达观测的反射率因子数据,加入MWR反演中进行训练能够有效地提高反演精度[33]。马舒庆[34]等就发展中的地基遥感大气廓线技术认为,多种探测仪器和数据的融合应当是今后的发展趋势。
鉴于现有BP神经网络反演方法的不足,本研究尝试构建长短期记忆神经网络(Long Short-Term Memory,LSTM)湿度廓线反演模型以提高反演精度。该模型创新性的以一段时间的地基微波辐射计连续观测数据作为反演的输入,再结合云雷达对云的观测数据解决云情况下的观测精度。模型以探空仪观测的数据作为真值,利用LSTM网络对高维廓线数据进行学习和训练,并估计湿度廓线。
1 设备及资料
1.1 数据来源
本试验所采用的MWR资料来源于中国气象局大气探测试验基地的Airda-HTG3型号的微波辐射计,拥有14通道,包含7个K波段水汽通道与7个V波段氧气通道,亮温接受灵敏度小于0.2 K(1 s 积分时间)。采用的是MWR所探测的亮温数据,平均每1 s采集到一组包含7个K波段水汽通道数据与7个V波段氧气通道数据。MWR每6个月进行液氮定标,天线罩定期清洁与更换,其他设备也均按气象业务规范进行日常维护。
毫米波云雷达为Ka波段多普勒雷达,其峰值功率4 W,波长为8.6 mm,天线工作方式为垂直顶空瞄准式,有效观测高度为15 km,垂直空间分辨率约为30 m,时间分辨率为1~60 s,试验中设置为60 s,最小探测粒子回波强度为-40 dBz。
探空数据为北京观象台(站点号:54511)每天所释放GTS1型数字探空仪作为基准数据。其每天释放时间为11:15(UTC,下同)和23:15,个别时间加密观测为05:15。为保证三种数据的时间一致,从探空气球释放时间开始,进行微波辐射计和毫米波云雷达数据的时间一致性的匹配。由于MWR有效测量高度为10 km左右,为保证数据高度的一致性,因此这三种数据的高度范围均选择0~10 km。并且,由于MWR在测量亮温时,收到的微波信号位于仪器天线的正上方附近,因此在廓线的垂直分辨率上选择不同的密度,依据Airda-HTG型号的MWR划分依据,在0~10 km范围内,选择采样间隔从密到疏的93个节点,即93层廓线。
1.2 质量控制
为了使模型有着较好的泛化性能,需确保数据的多样性。为此,本研究所选择的数据为2016年2月至2017年9月共20个月的数据,数据覆盖了春、夏、秋、冬四个季节,包含了复杂多样的大气湿度廓线样本。3种仪器(微波辐射计、毫米波云雷达、探空仪)所共同拥有的数据量样本例为858条,但因为一些数据样本例难以有效地反映出数据间隐藏的非线性关系,因此将数据送入到网络之前需要进行数据的筛选处理。
1.2.1 微波辐射计数据处理
由于在雨天时MWR天线罩上的雨滴会导致观测的数据出现异常值,因此本研究只涉及云天与晴天,对云雷达或探空仪所判定为雨天天气的亮温数据进行剔除,保留晴天与云天的样本。
并且,依据时间一致性原则,即观测亮温值应该是随时间变化而连续变化的,具有一定的规律,不应该出现太大的突变,若出现短时间内突变较大的样本,则有可能是因为设备自身观测时所产生的误差,将该样本标记为可疑样本,并剔除掉该样本。
1.2.2 云雷达数据处理
依据黄兴友[35]做出的云雷达回波强度Z分级,将数据划分为5个强度区间,弱云区:Z<-20 dBz,厚云区:-20 dBz≤Z<0 dBz,云中包含液水区:0 dBz≤Z<15 dBz,弱降水区:15 dBz≤Z<25 dBz,显著降水区:Z>25 dBz。因为本研究只考虑云天与晴天,所以依据上述5个分级,选择回波强度为-41~15 dBz区间中的样本。
1.2.3 探空数据处理
从探空数据来分析,依据Poore[36]的研究,有云形成时,其相对湿度为100%,但由于受到凝结核及多种因素的作用,实际相对湿度会低于这个数值。因此设定阈值为相对湿度85%,判定存在相对湿度高于85%的数据为云天数据,详细天气情况划分如下:①晴天:所有高度层的相对湿度都低于85%。②云天:近地面处相对湿度低于85%,600~10000 m范围内存在相对湿度高于85%的数据。③雨天:近地面至600 m以上的任意范围,相对湿度都在85%以上。
在进行探空数据的筛选时,筛除判定为雨天的数据,保留晴天与云天的数据。
对于云雷达判定为有云,而探空未探测出有云的样本例,剔除该样本。同样,对于探空判定为有云,而云雷达未探测出有云的样本里,剔除该样本。经过剔除雨天数据、亮温异常数据及云雷达与探空表现不一致数据后,原858条样本只保留748条数据用于实验,其中晴天样本数量为409条,云天样本数量为339条。
2 廓线反演方法
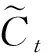
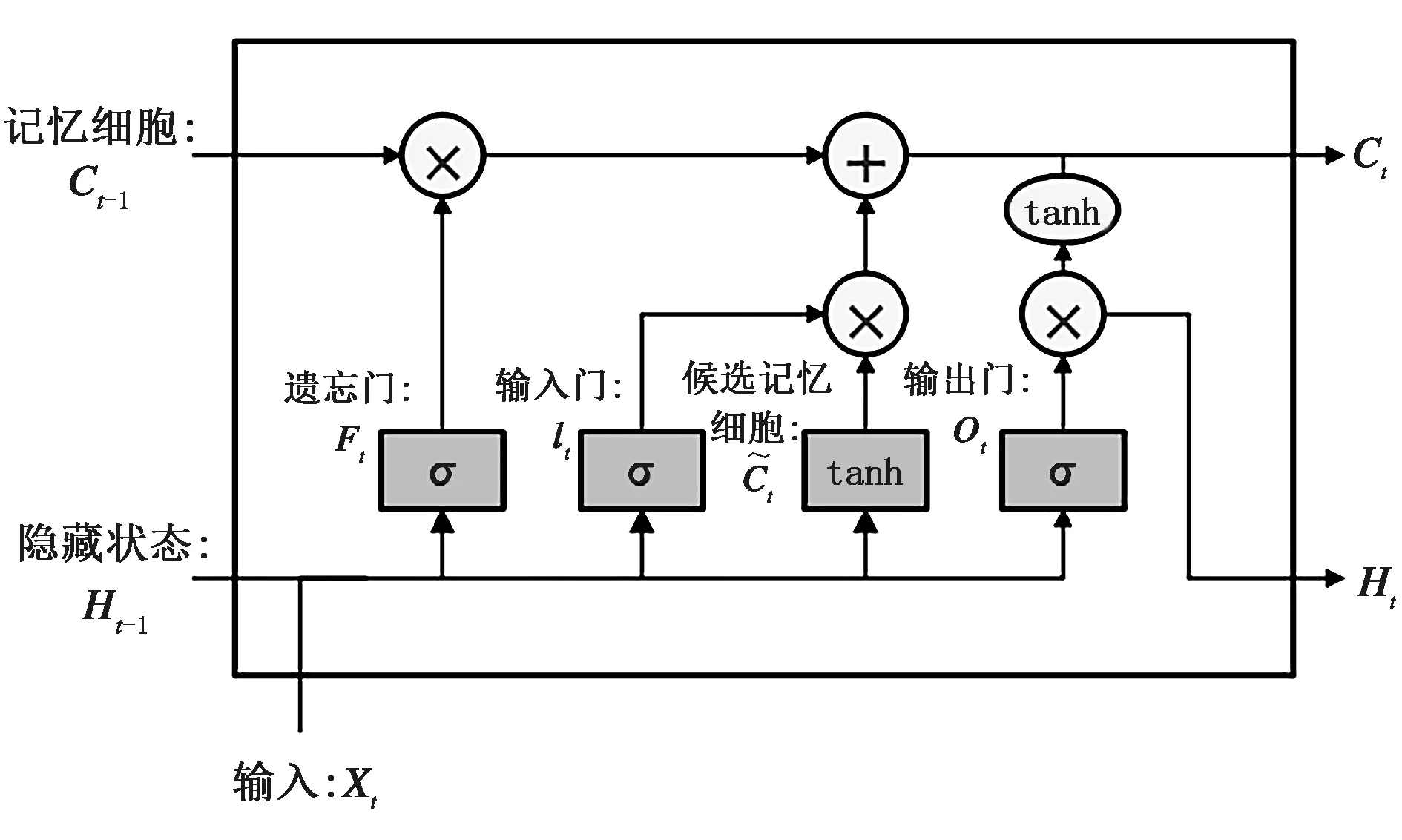
图1 长短记忆模型记忆单元结构示意
其公式表达如下,输入门、遗忘门和输出门:
It=σ(XtWxi+Ht-1Whi+bi)
(1)
Ft=σ(XtWxf+Ht-1Whf+bf)
(2)
Ot=σ(XtWxo+Ht-1Who+bo)
(3)
候选记忆细胞:
(4)
记忆细胞:
(5)
隐藏状态:
Ht=Ottanh(Ct)
(6)
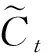
所有LSTM都包含神经网络重复模块链的形式,即图1所示的多个LSTM单元。时间序列有多长就有多少个LSTM单元,本研究使用20个长度的时间序列进行建模,因此cell的个数为20,即下图的t为20。在本文中,基于长短记忆模型框架构建了一个神经网络模型来反演大气湿度廓线。模型框架图如图2所示。其中X为输入单元,在本实验中表示一个时次的输入数据,是(60,1)的二维数据;t为20,表示输入时次的个数。
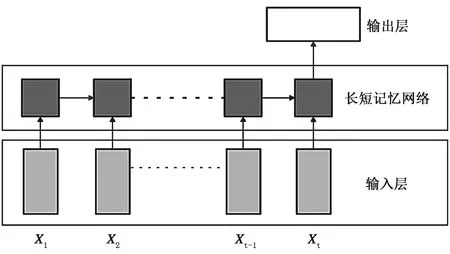
图2 长短记忆模型结构示意
在输入节点上包括3个信息来源,亮温数据、地面温湿压数据以及云雷达数据。MWR选择14个通道所测量的亮温数据以及其配置的地面传感器观测的3个地面温湿压数据。云雷达反射率原数据为30 m一个距离库,考虑到如果选取大量的反射率因子节点会使得在进行训练时收敛速度慢,计算量增加,影响反演效果。并且,唐英杰[37]在进行北京区域的云雷达和云高仪对云层的厚度统计中发现,云雷达在低云、中云和高云的平均云回波厚度分别为586、1475、920 m。因此在本试验选择的0~10 km高度输入中,将其分层为43层,层间距离为236 m,能够确保若天空中存在云时,不会将云给遗漏。因此输入节点选择14个通道亮温、地面温湿压与43个云雷达反射率共60个节点。由于探空仪在升空时是需要时间的,升至10 km高度时大约需要30 min,其探测获得的廓线信息同样包含着时间信息。然而,现有基于BP方法的反演研究并未考虑这一因素,为此,本试验将时间维度这一信息添加到反演研究中。在输入方面,将30 min的数据等间隔划分为20份,每份为1.5 min时间的数据平均,即输入维度为(20,60,1)的包含时间信息的三维数据。输出为(1,93,1)的湿度廓线。图3所示为本文反演模型数据网络结构。
为了评估算法效果,本研究选取了BP神经网络与SVM(support vector machines)支持向量机反演方法进行对比,将一段时间亮温数据进行平均,采用数据平均值进行训练,输入数据为维度为(60,1)的二维数据,输出为(93,1)的湿度廓线。图4为不添加时间信息的经典模型数据网络结构。
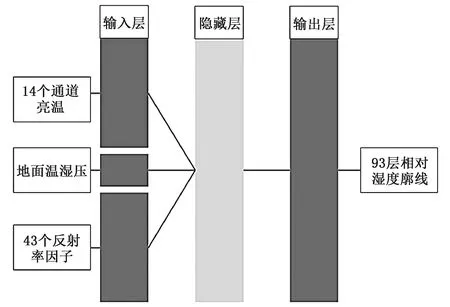
图4 BP神经网络反演结构
将2016—2017年两年共748条数据进行打乱处理,按照3∶1的比例划分为训练集与测试集进行训练。本文中SVM方法使用python中的sklearn机器学习库,LSTM与BP方法使用python中pytorch深度学习框架。经试验,最终使用MSE(Mean Square Error)作为损失函数,Relu(Rectified linear units)作为激活函数,有效地避免了出现梯度爆炸与消失的问题。训练样本与测试样本之间相互独立。使用LSTM做训练时,经过多次训练及对各个训练参数的调整,选择其中最优的网络模型并保存。
3 试验结果与分析
为了测试本文所提出的模型的性能,以探空数据作为真值,计算93层不同高度上的反演结果的均方根误差RMSE,平均绝对误差MAE。
(7)
(8)
式中,RMSE为均方根误差,MAE为平均绝对误差,m为廓线高度层93,y′为模型反演结果,y为探空观测数据。
首先比较了本文所提出模型的训练结果和探空仪真值的线性回归结果。图5为LSTM模型预测值与探空观测值的散点分布情况。图中给出了数据的相关系数以及其均方根误差。彩色区域表述数据点的密度,红色的高核密度值表示大部分数据所在的位置。预测值与观测值的线性回归关系斜率为0.7,y轴截距为10.95,相关系数(R)为0.84,均方根误差(RMSE)为13.85%。实验数据说明了本文提出的模型反演值与探空数据具有较高的一致性。
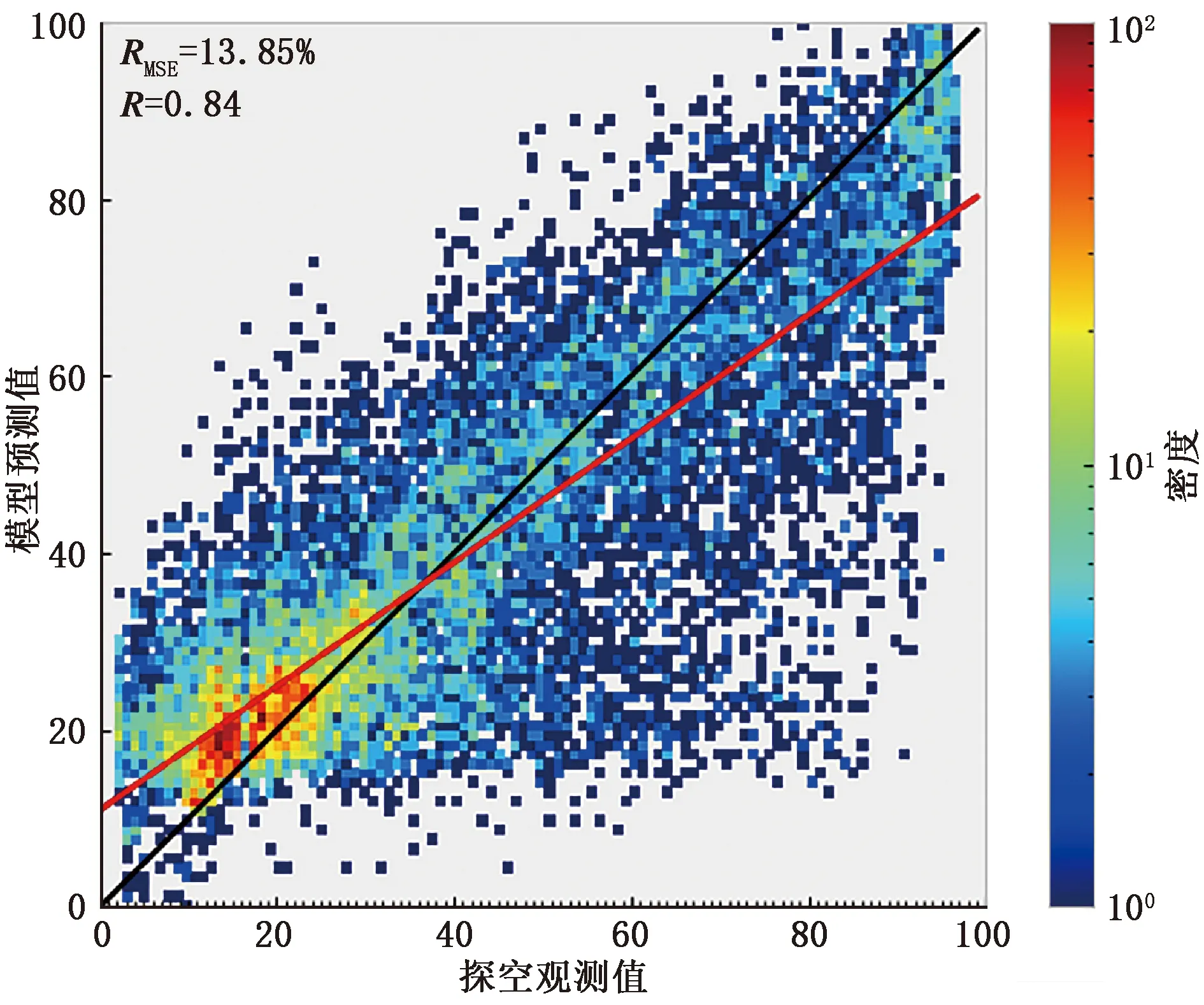
图5 LSTM模型预测值与探空观测值数据分布散点(黑色实线是y=x标准线,红色实线为数据拟合线)
对187组验证数据进行统计,本文模型和常规方法BP、SVM所得到的反演结果同探空所测量的实际相对湿度进行对比,其结果如表1所示。其中,本文提出模型的均方根误差为13.85%,平均绝对误差为9.80%; BP方法的均方根误差为15.66%,平均绝对误差为11.52%;SVM方法的均方根误差为18.90%,平均绝对误差为14.49%。可以发现,本文基于LSTM的反演结果不论是RMSE还是MAE都要优于不添加序列探测信息的BP与SVM的反演效果。
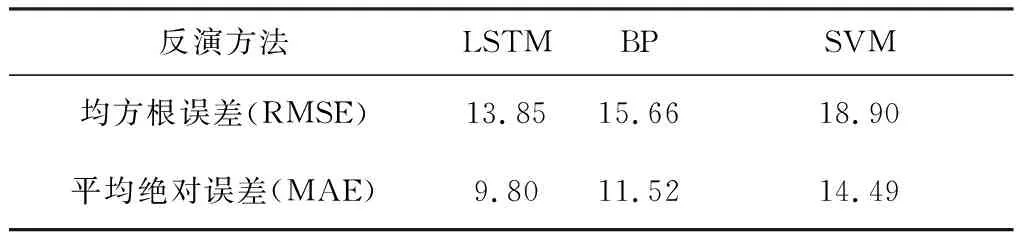
表1 LSTM、BP、SVM 3种方法反演相对湿度误差 %
为对各个高度层进行精细分析,我们对验证数据的反演结果进行统计并给出在0~10 km的93层不同高度层上本文LSTM模型和BP与SVM反演方法所对应的相对湿度廓线的均方根误差、平均绝对误差以及预测结果同探空对比,其结果如图6所示。从图中能够看出,3种方法在93层不同高度上具有较好的一致性,在近地表至3 km的范围中,LSTM和BP方法在反演方面有着更好的表现,在3~10 km处,LSTM方法的精度最好。整体来讲,添加时序观测数据后的LSTM的反演效果明显优于经典BP与SVM方法的反演效果,其中BP方法的表现要优于SVM方法。

图6 LSTM、BP、SVM 3种方法反演的相对湿度均方根误差
图7为本文使用的3种方法在验证数据中的反演结果同探空数据的对比,在0.3~2 km和3~7 km处,LSTM的结果明显优于不添加时间信息的结果,其中,在4.4 km处,二者差距最大为10.3%。在7 km以上的高空,二者的反演能力相似。从整体的93层廓线来看,本文的LSTM的反演结果更加接近于真实的探空廓线。

图7 LSTM、BP、SVM 3种方法反演的与探空相对湿度廓件
图8和图9分别为3种反演方法在验证数据中的反演结果同探空数据对比的平均绝对误差与平均偏差。从平均绝对误差图中能够看出,整体来讲,本文LSTM的反演结果同经典模型反演结果的平均绝对误差变化趋势有着较好的一致性。在0~3 km处,LSTM与BP反演效果相差不大,都优于SVM的反演效果。而在3~5 km处反演结果的平均绝对误差突然增大,考虑这一高度范围内的水汽廓线分布情况比较复杂,BP与SVM反演方法对于这种突然变化反应不够迅速,无法及时准确的描绘出其变化趋势。但是能够明显地看出,学习了一段时间观测数据的LSTM的反演方法能够更好地学习到这种变化,使其误差明显要小于经典神经网络的反演方法。在5~10 km处,二者平均绝对误差较为稳定,LSTM效果最优;但从平均偏差MBE的结果图中来看,在高空处LSTM数值要大于BP与SVM,说明反演结果在真值附近波动较大,而LSTM反演结果更加接近于真值。总体来讲,利用了时序观测数据的LSTM反演方法能够更好地学习到湿度在不同高度的变化,在细节的刻画方面要优于经典的神经网络的反演方法,能够获得更好的反演效果。

图8 LSTM、BP、SVM 3种方法反演的相对湿度平均绝对误差
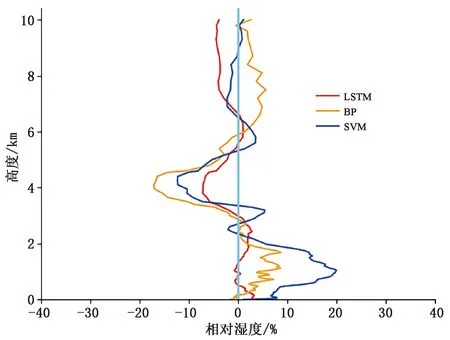
图9 LSTM、BP、SVM 3种方法反演的相对湿度平均偏差
为进一步验证本试验中所提出的模型的反演能力,在验证数据中选取了如图10所示的不同湿度水平的3个探测个例进行对比。从图10能够看出,3种反演结果与探空数据都比较接近,都能够在一定程度上描绘出相对湿度的变化趋势,但是明显能够看出LSTM的表现要更加优异,更加接近于真实的探空廓线数据。
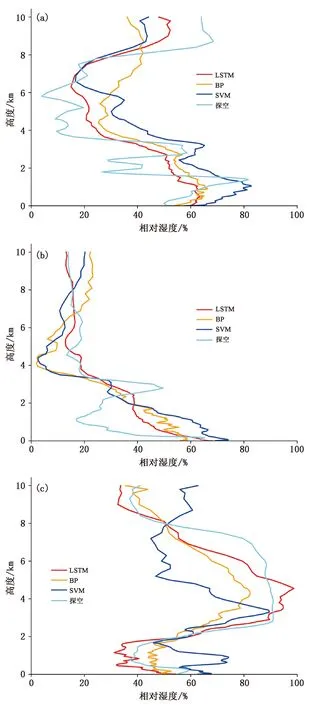
图10 LSTM、BP、SVM 3种方法反演的个例的相对湿度均方根误差:(a)2017年5月25日11:15,(b)2017年9月7日11:15,(c)2017年4月11日11:15
此外,本文使用LSTM模型对反演数据中是否添加云雷达信息做了对比试验,未添加云雷达数据对大气湿度廓线反演结果均方根误差为16.24%,与添加云雷达数据的反演均方根误差13.85%有着较大差距,其各层均方根误差如图11所示。其中红色的线为添加云雷达数据的反演结果,橙色的线为未添加云雷达数据的反演结果,能够看出,在近地面处二者结果比较接近,而在其余高度层添加云雷达数据的反演效果要优于未添加云雷达数据的反演效果。总体来讲,云雷达数据对大气湿度廓线的反演效果起到了明显的改善作用。
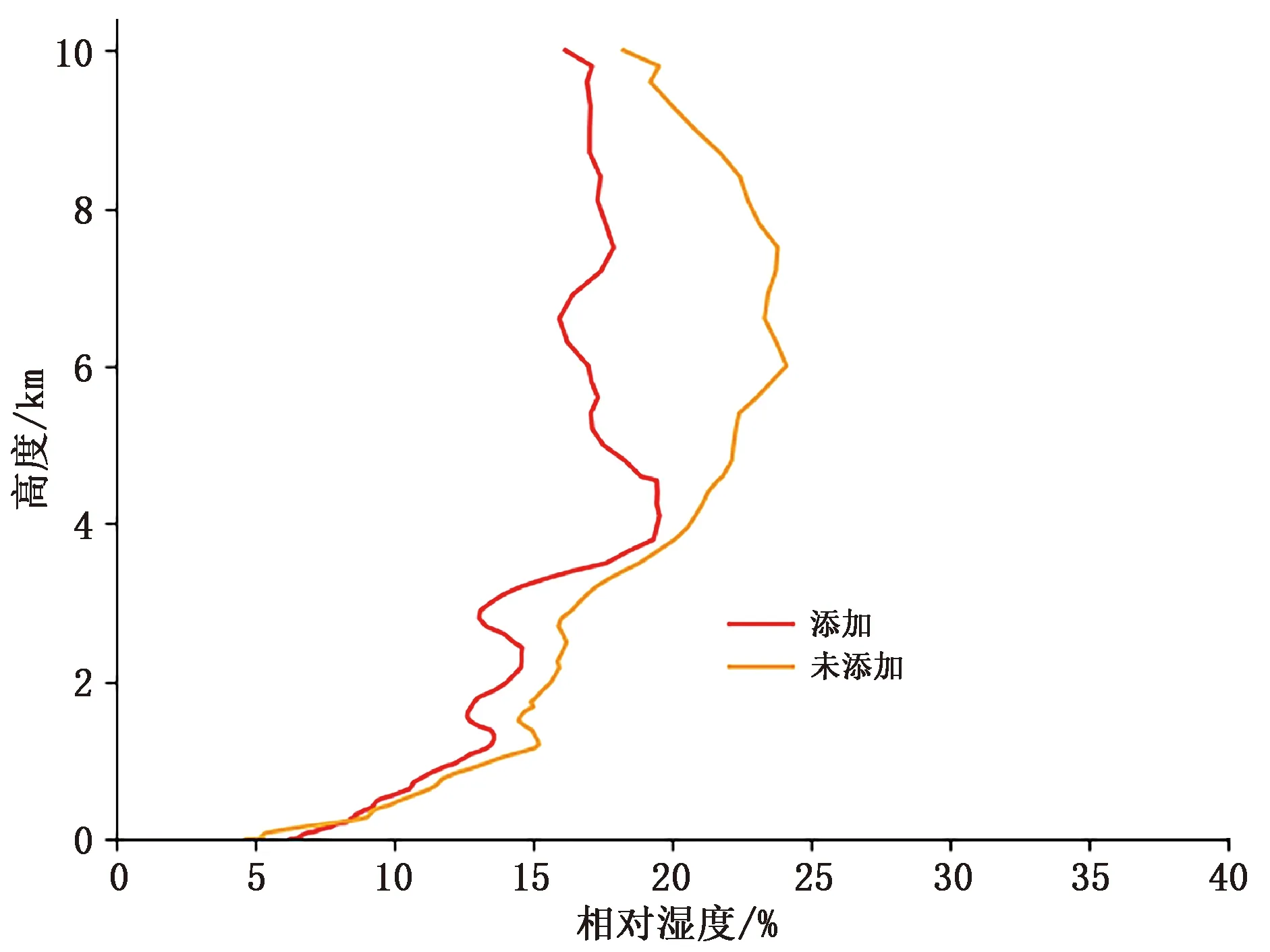
图11 添加云雷达数据和未添加云雷达数据LSTM法反演的相对湿度均方根误差
4 结论与讨论
本文尝试利用长短期记忆网络,将包含时序观测数据的微波辐射计14通道的亮温数据结合Ka波段毫米波云雷达所探测的反射率因子数据进行大气湿度廓线的反演计算,用探空仪实测相对湿度数据作为真值验证并分析反演效果。
结果表明LSTM对0~10 km范围中共93层大气湿度廓线的反演结果的均方根误差与平均绝对误差分别为13.85%与9.80%,具有较好的反演能力。此外,在相同的训练和测试数据下,比较了添加时间信息的反演方法与不添加时间信息的反演方法的性能。对比结果表明,相比与BP、与SVM,LSTM的反演结果与探空数据的相关性更好,差异更小。特别是3~7 km大气湿度廓线分布比较复杂的范围内,LSTM有着更好的表现。
本文证明了添加时序信息是一种有效的反演大气湿度廓线的方法。实验说明加入时序信息可以改善MWR的反演效果,以获得精度更高的大气湿度廓线。
本文大气湿度廓线的反演结果中,能够看到较好的效果,但受限于样本的数量,作为数据驱动型技术的深度学习未能充分发挥出该方法的优势,同时,由于MWR亮温的稳定性与云雷达的衰减,最终反演结果精度还有待提高。后期将进一步增加数据量,对数据进行严格的质量控制,以期充分发挥出深度学习的优势,提高反演的精度,并进行大气温度廓线的反演研究。

