混合次分数布朗运动机制下带有随机利率的欧式期权定价模型

王欣怡，郭志东

（安庆师范大学 数理学院，安徽 安庆 246133）

期权定价问题是金融数学的研究热点之一，最为经典的期权定价模型由Black和Scholes在1973年提出，模型假设标的资产价格S t的变化服从几何布朗运动[1]，即

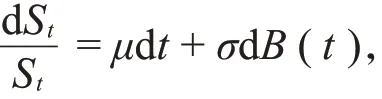
其中，μ,σ为常数，B(t)为标准的几何布朗运动。因为Black-Scholes（BS）模型的随机驱动源是几何布朗运动，所以它无法刻画金融资产价格变化的长程相关性、重尾分布等特征。为了克服布朗运动的这一不足，许多学者提出了次分数布朗运动，并建立了次分数布朗运动驱动下的期权定价模型。Araneda等建立了混合次分数布朗运动CEV模型，运用伊藤公式得到相关的Fokker-Planck方程，根据M-Whittaker函数和非中心卡方分布函数，得到了欧式看涨期权的价格[2]。实证结果表明此模型比标准的CEV模型更优。徐峰等建立了混合次分数布朗运动下交换期权的定价模型，利用混合次分数布朗运动的相关理论和偏微分方程方法，得到了交换期权的定价公式[3]。杨月等建立了次分数布朗运动下带跳跃的几何亚式期权定价模型，利用自融资交易策略和变量替换法给出了几何亚式期权的定价公式，通过数值分析得到赫斯特指数和跳跃强度对亚式期权价格的影响[4]。梁喜珠等和王瑞等建立了次分数布朗运动下最值期权和后定选择权的定价模型，利用保险精算的方法，得到最值期权和后定选择权的定价公式[5-6]。

上述文献均假设利率为常数，而事实是利率随时间的变化而变化，于是一些学者提出了随机利率模型，如Vasicek模型[7]、Merton模型[8]等。史言建立了一个包含随机利率因素的混合指数跳扩散模型，利用快速傅里叶变换算法和模型特征函数得到欧式期权定价的快速数值解[9]。王之渊等提出了基于Klein模型的跳扩散过程下带有随机利率的脆弱期权定价模型，利用伊藤公式和鞅方法得出脆弱看涨期权定价公式[10]。基于此，本文研究混合次分数布朗运动机制下带有Merton随机利率的欧式期权定价问题。

1 混合次分数布朗运动

定义1[2]满足条件ξH(0)=0,E[ξH(t)]=0和

的高斯过程ξH={ξH(t),t≥0}称为次分数布朗运动。当时，B H(t)为标准的几何布朗运动B(t)。

定义2[2]称{Mβ,γ,Ht,t≥0}=Mβ,γ,H=βB t+γξHt,β≥0,γ≥0为混合次分数布朗运动，其中B t为几何布朗运动，ξHt为次分数布朗运动。

由定义1和定义2可知：

当β=0,γ=1时，Mβ,γ,Ht为次分数布朗运动；当β=1,γ=0和时，Mtβ,γ,H为标准布朗运动。

2 零息票债券的定价公式

假设利率r(t)满足

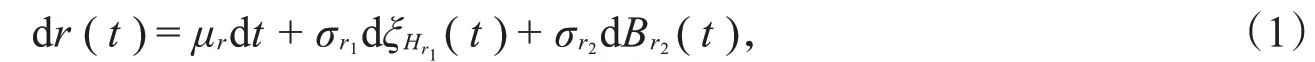
其中，μr,σr1,σr2是常数，ξH(t)是次分数布朗运动是标准的维纳过程，ξH r1(t),B r2(t)相互独立。

设P(r,t;T)为零息票债券在t时刻的价格，当r(t)满足式（1）时，由泰勒公式可知

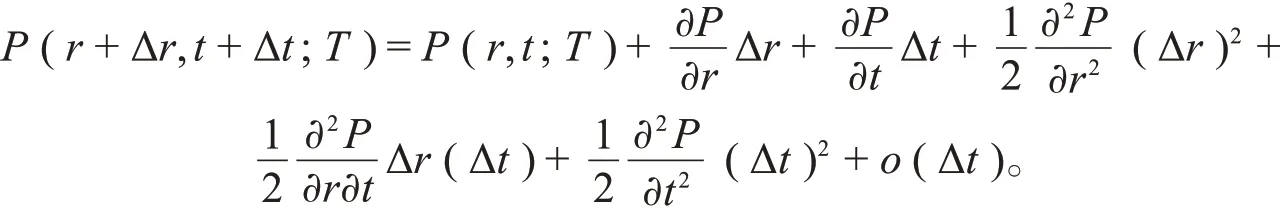
由式（1）得

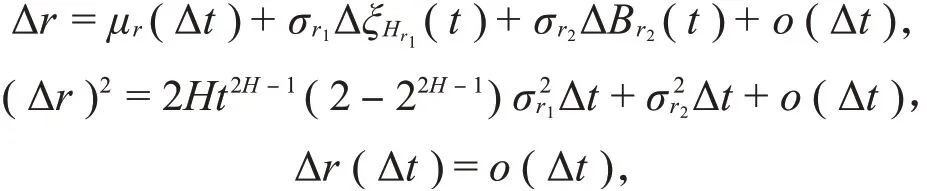
因此

因此，零息票债券P(r,t;T)满足偏微分方程和边界条件

令τ=T-t，P(r,t;T)=eA1(τ)-rA2(τ)，得

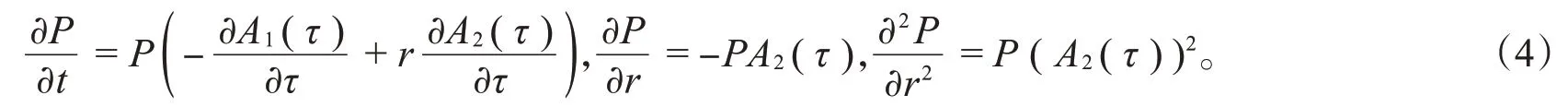
把式（4）代入式（2），得

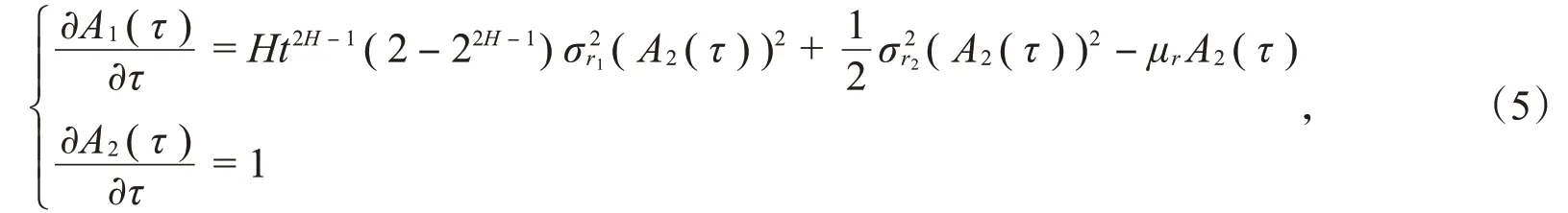
因此，零息票债券的定价公式为P(r,t;T)=e-rτ+A1(τ)。

3 欧式期权定价的BS公式

假设标的资产价格S(t)满足随机微分方程

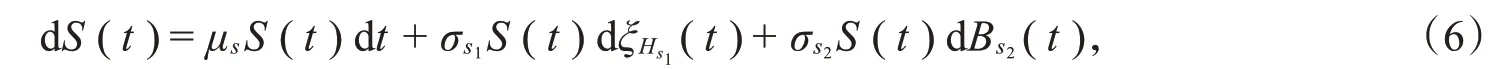
其中，μs,σs1,σs2是常数，ξH(t)是次分数布朗运动，是标准的维纳过程，ξH s1(t),B s2(t)相互独立。记K为敲定价格，T为欧式看涨期权的到期日，c=c(S,r,t)为看涨期权价格，当r(t)满足式（1），S(t)满足式（6）时，得到如下结论。

定理1c(S,r,t)满足以下BS偏微分方程

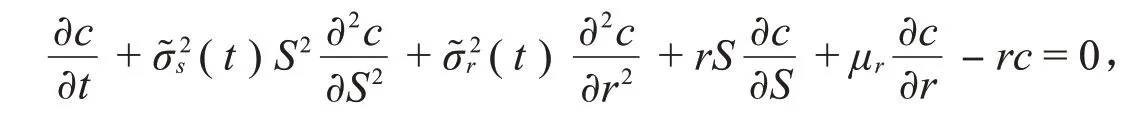
证明考虑投资组合由c(S,r,t),Δ1t,Δ2t构成，Δ1t表示标的资产的份额，Δ2t表示零息票债券的份额，投资组合在t时刻的价格为Πt=c t-Δ1t S t-Δ2t P t，则

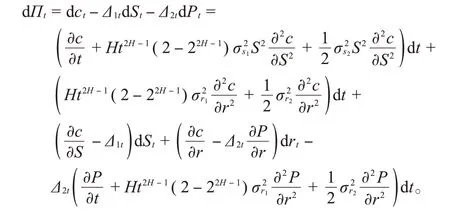
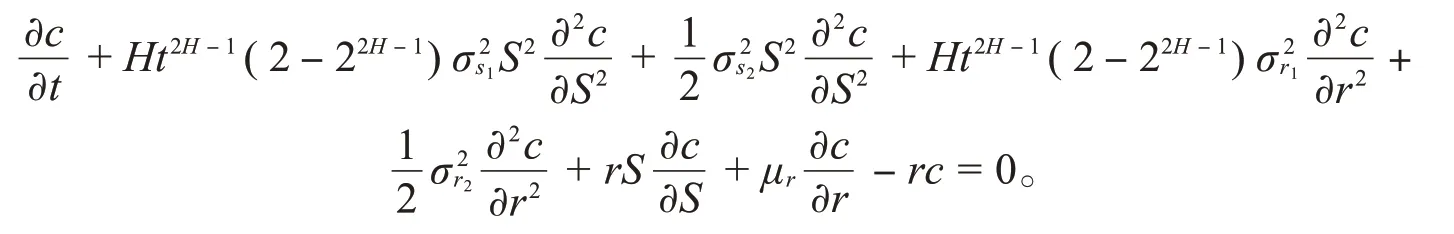
4 新模型下的欧式期权定价公式

现给出混合次分数布朗运动机制下带有Merton随机利率的欧式期权定价公式。

定理2当r(t)满足式（1），S(t)满足式（6）时，通过到期日T和敲定价格K，得到欧式看涨期权的定价公式为c(S,r,t)=SN(d1)-KP(r,t;T)N(d2)；看跌期权的定价公式为p(S,r,t)=KP(r,t;T)N(-d2)-SN(-d1)；看涨-看跌期权的平价公式为c(S,r,t)-p(S,r,t)=S-KP(r,t;T)，其中，

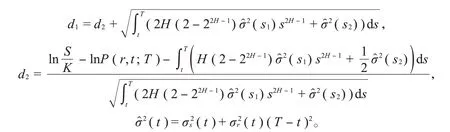
证明欧式看涨期权的收益为c(S T,r,T)=(S T-K)+，欧式看涨期权满足

通过计算可得

把式（10）代入式（8），得

零息票债券价格P(r,t;T)满足式（8），因此c^(y,t)满足

且有边界条件

其中，

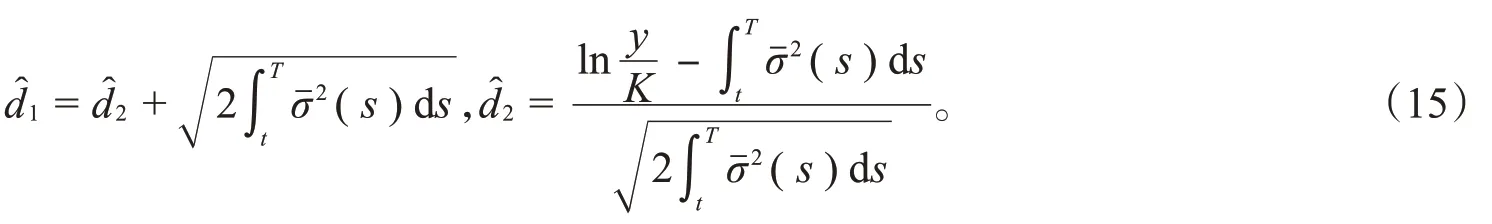
由式（9）和式（14）～（15）得c(S,r,t)=SN(d1)-KP(r,t;T)N(d2)，其中，

以及看涨-看跌的平价公式c(S,r,t)-p(S,r,t)=S-KP(r,t;T)。

5 隐含波动率

下面给出模型下的隐含波动率。

推论当t=0时，欧式看涨期权的定价公式为(K,T)=S0N()-KP0N()；看跌期权的定价公式为(K,T)=KP0N(-)-S0N(-)，其中，

此时，σim为相对于经典BS模型的隐含波动率。

6 数值计算与结论

下面给出本文模型的数值计算过程，并与一些经典模型进行对比分析。参数选取如下：

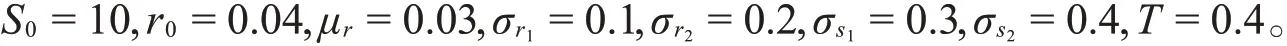
表1给出了敲定价格K取不同值时，混合次分数布朗运动机制下带有Merton随机利率的欧式看涨期权价格c1的变化。从表1可以看出，敲定价格K越大，欧式看涨期权价格越小；随着参数H的增大，欧式看涨期权价格逐渐减小。表2给出了敲定价格K=10、初值S0取不同值时，混合次分数布朗运动机制下带有Merton随机利率的欧式看涨期权价格c2的变化。从表2可以看出，S0越大，欧式看涨期权价格越大；随着参数H的增大，欧式看涨期权价格越小。

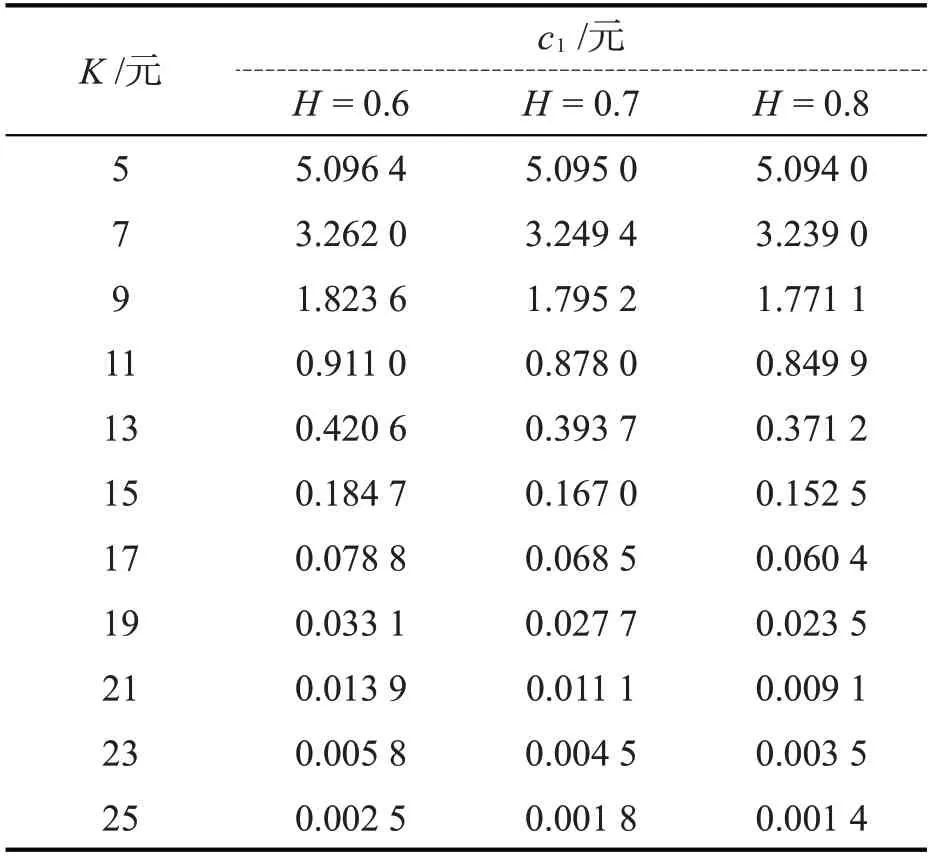
表1 不同敲定价格K和H下c 1的比较

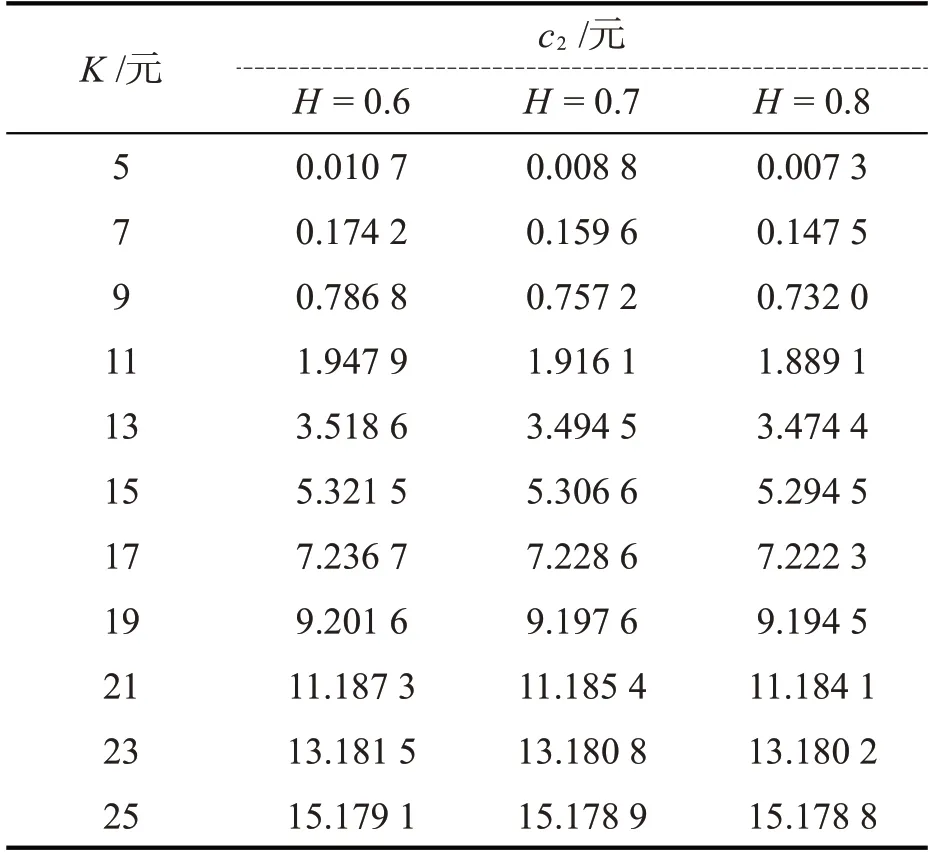
表2 不同S0和H下c2的比较

表3给出了在不同敲定价格K下，c1与经典的BS模型下的欧式看涨期权价格cBS之差的比较。从表3可以看出，当敲定价格K取不同值时，混合次分数布朗运动机制下带有Merton随机利率的欧式看涨期权价格总是大于经典的BS模型下的欧式看涨期权价格。表4给出了在不同敲定价格K下，c1与经典的Merton随机利率模型下的欧式看涨期权价格c3之差的比较。从表4可以看出，当敲定价格K取不同值时，混合次分数布朗运动机制下带有Merton随机利率的欧式看涨期权价格总是大于经典的Merton随机利率模型下的欧式看涨期权价格。

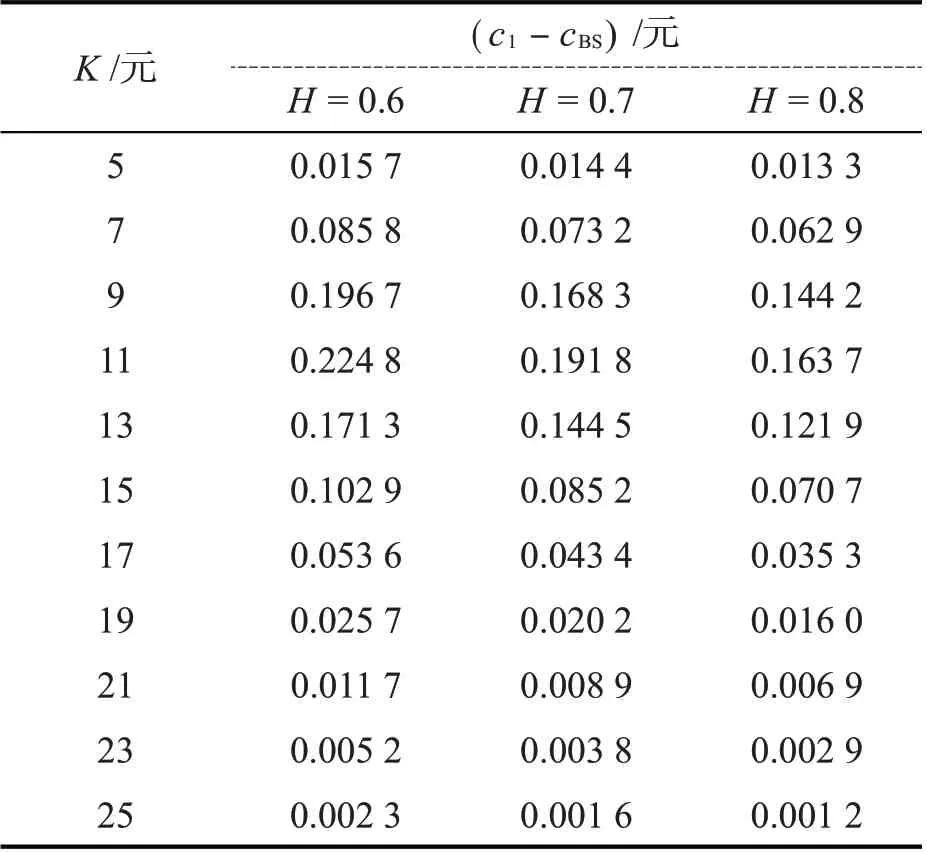
表3 不同K和H下c 1与c BS的价格之差

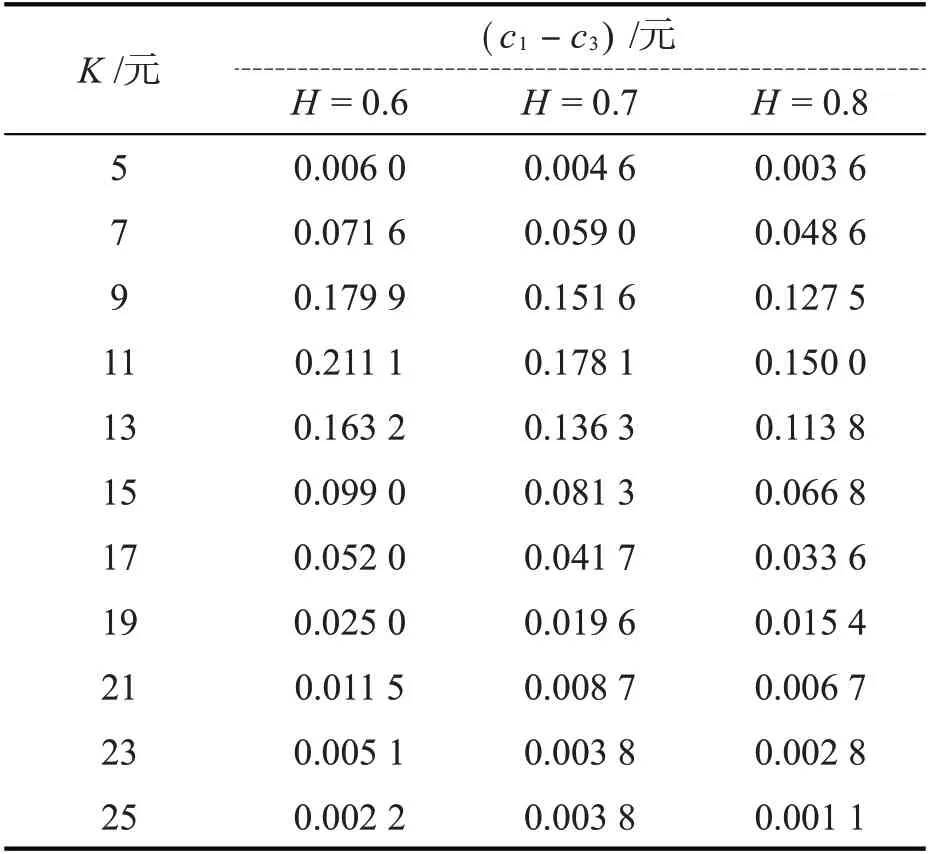
表4 不同K和H下c 1与c 3的价格之差

综上所述，本文以混合次分数布朗运动作为随机驱动源，同时将随机利率纳入期权定价模型中，得到了该模型下欧式期权的显示定价公式。数值计算结果表明，模型下欧式期权的定价要高于经典BS模型和经典Merton随机利率模型，这与实际金融市场中期权的定价相符。不足之处在于我们只研究了欧式期权定价，后续可以深入研究随机利率模型下美式期权、新型期权的定价问题。