Optimization for vibro-impact nonlinear energy sink under random excitation

Jiamin Qian, Lincong Chen,*

a College of Civil Engineering, Huaqiao University, Xiamen 361021, China

b Key Laboratory for Intelligent Infrastructure and Monitoring of Fujian Province, Huaqiao University, Jimei Avenue 668, Xiamen, Fujian, 361021, China

Keywords:Vibration control Vibro-impact NES Stochastic averaging Optimization

ABSTRACT As a promising vibration control device, the vibro-impact nonlinear energy sink (VI-NES) gathered extensively attention in recent years. However, general optimization procedures have not been available for the design of VI-NES subjected to random excitations. To this end, this paper constitutes a research effort to address this gap. Specifically, the approximate analytical solution of the system stochastic response is obtained in conjunction with non-smooth conversion and stochastic averaging methodology. Taking advantages of this approximate solution, the variance of the system is defined and easily minimized to calculate the optimal parameters for VI-NES. In addition, the results computed by this way fairly correlate with direct numeric simulations.

Excessive vibrations, such as those stimulated by strong wind and severe earthquake, tend to reduce the comfort of user, shorten structure lifespan, and in extreme cases lead to structural failure or even large number of casualties [1]. The attachment of nonlinear energy sink (NES) induces targeted energy transfer (TET)in an irreversible manner, thus effectively attenuating undesirable vibration [2,3]. Among various forms of NES, employing the nonsmooth nonlinear element in NES which is termed as vibro-impact NES (VI-NES) [4,5]. The competence of VI-NES in reducing structural response has been confirmed numerically, theoretically and experimentally [6–8]. However, due to the nonlinear properties of the VI-NES and external stimuli including strong winds or severe earthquakes are random in nature, obtaining a clear analytical solution of VI-NES damper system (VI-NES-DS) under random loads still poses a challenge. In addition, general and cost-effectively optimization procedures have not been available for the design of VI-NES. This work constructs an analytical optimization procedure of VI-NES-DS subjected to random excitation. By resorting to non-smooth transformation and stochastic averaging method(SAM) [9,10], the approximate probability density function (PDF)of the VI-NES-DS can be determined in a closed form. On this base, a procedure to optimize the parameters of the system is established minimizing the displacement variance of the VI-NESDS. Finally, numerical demonstrations are performed and related results are compared with pertinent data obtained by Monte Carlo simulations (MCS).

Consider a single-degree-of-freedom main structure (MS)equipped with a VI-NES device, as displayed in Fig. 1. In this paper,we only concern with the horizontal motion of the structure under the base excitationXg. Note that the rolling motion of the added mass is often ignored in other studies. We introduced an inerter to consider the influence of the complex rolling state of added mass on the damping mechanism, as presented in Fig. 1b. The governing equation of the inerter is given by

wherex1(t): the absolute displacements of MS;x2(t): the absolute displacements of VI-NES.

Note that the collision is completed in an instant, the velocity jump relationship between the MS and VI-NES before and after the collision can be expressed by

Reference [12] has been exerted this condition to analysis the uncertainty quantification of spatial variability in the constitutive parameters of concrete in structures. We can easily note that these two types of motions are independent. In this case, the analysis of the MS and nonlinear VI-NES allowed to be performed separately.Substitute Eq. (4) into Eq. (3) yields

Fig. 1. (a) SDOF main structure incorporating the VI-NES configuration; (b)Schematic representation of the inerter device.

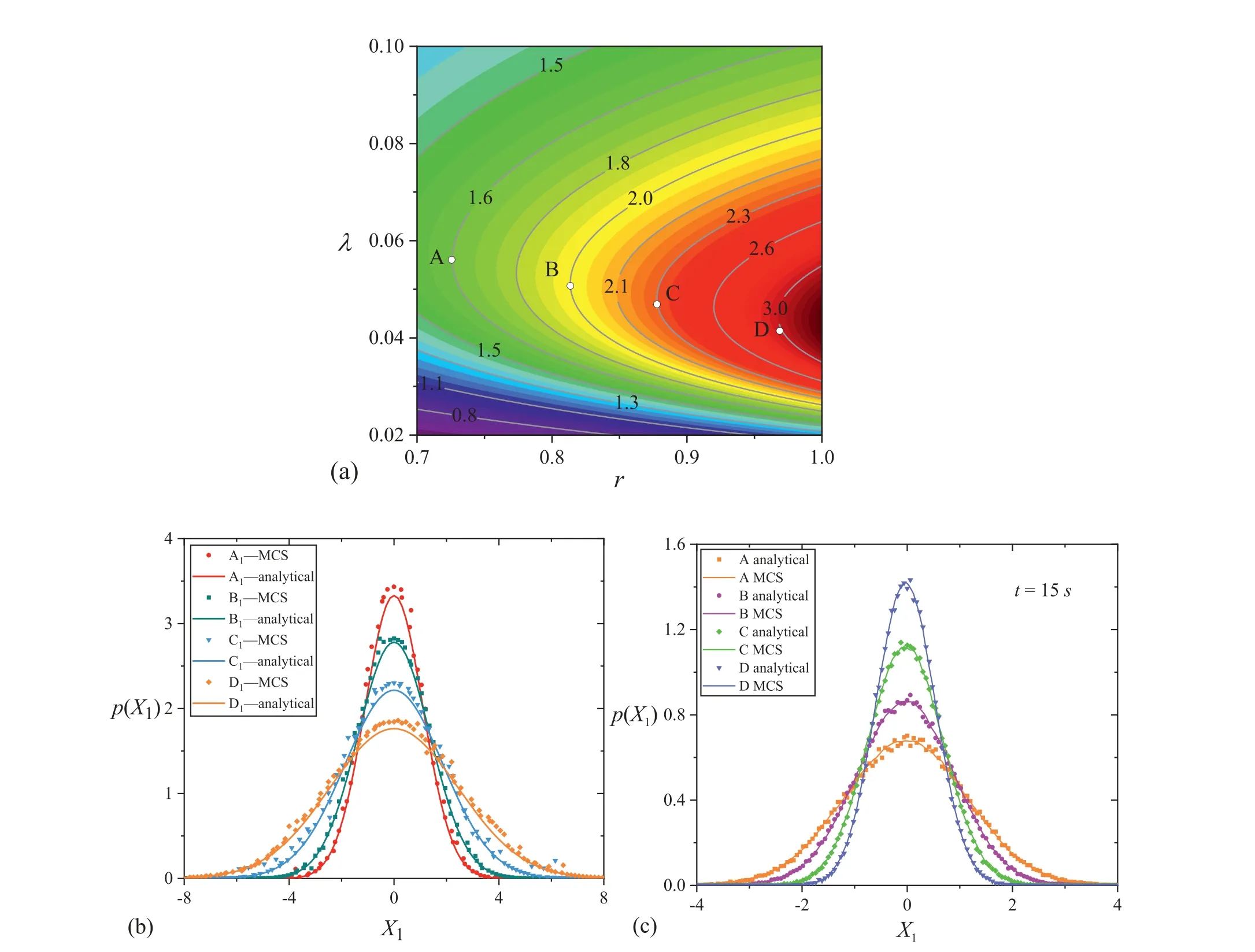
Fig. 2. (a) Contour plot of Eq. (22); (b) The stationary PDF of MS for points A, B, C, D; (c) The transient PDF of MS for points A, B, C, D. (β1=0.5, β2=0.4, ω1 = 1.0,ω2 = 1.095, D = 0.5, ε= 5%)

by denoting

As evident from Eq. (5), the state of MS is hardly affected by the impact. While the mutation of the velocity sign renders the VI-NES non-smooth and therefore strongly nonlinear. Fortunately,the discontinuity in VI-NES can be addressed by calling the nonsmooth transformation [13]. The non-smooth transformation shifts the impact barrier to the axisv2=0 and maps the domainu2＞0 of phase-plane trajectories on the original plane (u2, ˙u2) onto the whole phase plane (v2, ˙v2). Therefore, in a special case of elastic impact (r= 1) the transformed response velocity is found to be continuous during impact, and the transformed problem can be solved without taking into account the(transformed) impact condition (2), which would be satisfied automatically. Thus, we define

whereγ12=C2,γ22=C6. Note that theAi(t) (i=1,2) is independent of the phaseΘi(t) (i=1,2), which can be regarded as an approximate Markov process [14]. To this end, the SAM can be manipulated to yield the following Itô equation forAi(t) (i=1,2)

whereB(t) is the process of a unit Wiener; ¯mi, ¯σi(i=1,2) are drift and diffusion terms, respectively

wherepj(j=u1,v2) signifies PDF of amplitudeAi(i=1,2). The boundary conditions of Eq. (14) with respect toAi(i=1,2) are

wherevstands for the design variable vector {r, λ},R1is the predetermined feasible domain of thev; R2denotes the set of values of mass ratioε.

SettingR2= 5%, with adjusting the inertance ratio and the RC simultaneously, the change trends for the RMS of MS displayed in Fig. 2. As illustrated in 2-D contour plots, there is an optimal combination of RC and inertance ratio that minimize the objective function within the permissible range.

To verify the reliability of proposed optimization formula, we give Fig. 2b which shows the stationary response of MS at the selected point in Fig. 2a, respectively. From points A to D, the stationary response of the MS spreads to both sides and the peak value decreases. It demonstrates that the vibration reduction performance of VI-NES is significantly diminished when RC is small.The transient response in Fig. 2c yield the same results. Besides, it is clear that the numerical outcomes are extremely identified with the results of the theoretical computation. On the whole, the proposed scheme is an efficient strategy for enhancing damping performance of the VI-NES.

This work constructs an optimization procedure of VI-NES-DS subjected to random excitation. Resorting to the non-smooth transformation, the closed-form solutions of the system stochastic response can be achieved by the SAM in conjunction with the Jacobian determinant. Then, an optimization procedure for the design of the VI-NES-DS based on the obtained solutions and the minimization of the structural displacement variance is proposed.Notably, numerical analyses have confirmed the validity of the analytical solutions, proving that the proposed scheme can be a potentially effective method for designing VI-NES.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgment

This work is supported by the National Natural Science Foundation of China (No. 12072118), the National Natural Science Funds for Distinguished Young Scholar of the Fujian Province of China(No. 2021J06024), and the Project for Youth Innovation Fund of Xiamen (No. 3502Z20206005).