Sedimentation motion of sand particles in moving water (I): The resistance on a small sphere moving in non-uniform flow☆,☆☆
Shu-Tang Tsai
Institute of Mechanics, Academia Sinica (Chinese Academy of Sciences), Beijing 100190, China
ABSTRACT In hydraulics, when we deal with the problem of sand particles moving relative to the surrounding water, Stokes’formula of resistance has usually been used to render the velocity of sedimentation of the particles. But such an approach has not been proved rigorously, and its accuracy must be carefully considered. In this paper, we discuss the problem of a sphere moving in a non-uniform flow field, on the basis of the fundamental theory of hydrodynamics. We introduce two assumptions: i) the diameter of the sphere is much smaller than the linear dimension of the flow field, and ii) the velocity of the sphere relative to the surrounding water is very small. Using these two assumptions, we solve the linearized Navier-Stokes equations and equations of continuity by the method of Laplace transform, and finally we obtain a formula for the resistance acting on a sphere moving in a non-uniform flow field.
1. Introduction
In the study of river-bed dynamics [1], when dealing with the relative motion between sand particles and the surrounding water,Stokes’drag formula is usually used to determine the relative velocities of the sand particles in water. The validity of this approach,however, has not been rigorously established and thus must be carefully discussed. In two previous articles [2], we discussed the sedimentation motion of sand particles in quiescent water, and obtained the correction to Stokes’formula for calculating the resistant forces on sand particles under this situation. To further study the sedimentation of sand particles in moving water, in the present paper we start from the fundamental theory of hydrodynamics and analyze the resistance forces on a sphere moving in a general flow field. We obtain a formula for the total resistance force. With the help of that, we will be able to study the relative velocities between sand particles and the surrounding water, and to understand the sedimentation process of sand particles in rivers.
2. Derivation of the resistance formula
2.1. Decomposition of the velocity and the drag force
Consider a flow field consisting of a viscous fluid in space, with proper initial and boundary conditions on the relevant hydrodynamic variables such as velocity and pressure. Suppose we now put a sphere with radiusainto the flow field, while keeping the initial and the boundary conditions of the flow in regions far away from the sphere unchanged, then a new flow state is established,which we would like to analyze. We take a coordinate system moving with the sphere, with the origin on the center of the sphere.We use Cartesian tensors to describe the motion. We denote the velocity of the sphere asviand the rotation tensor of the sphere asωij. Before the sphere is put into the flow field, the momentum equation and the continuity equation of the fluid are, respectively,





Table 1 Laplace transform pairs.


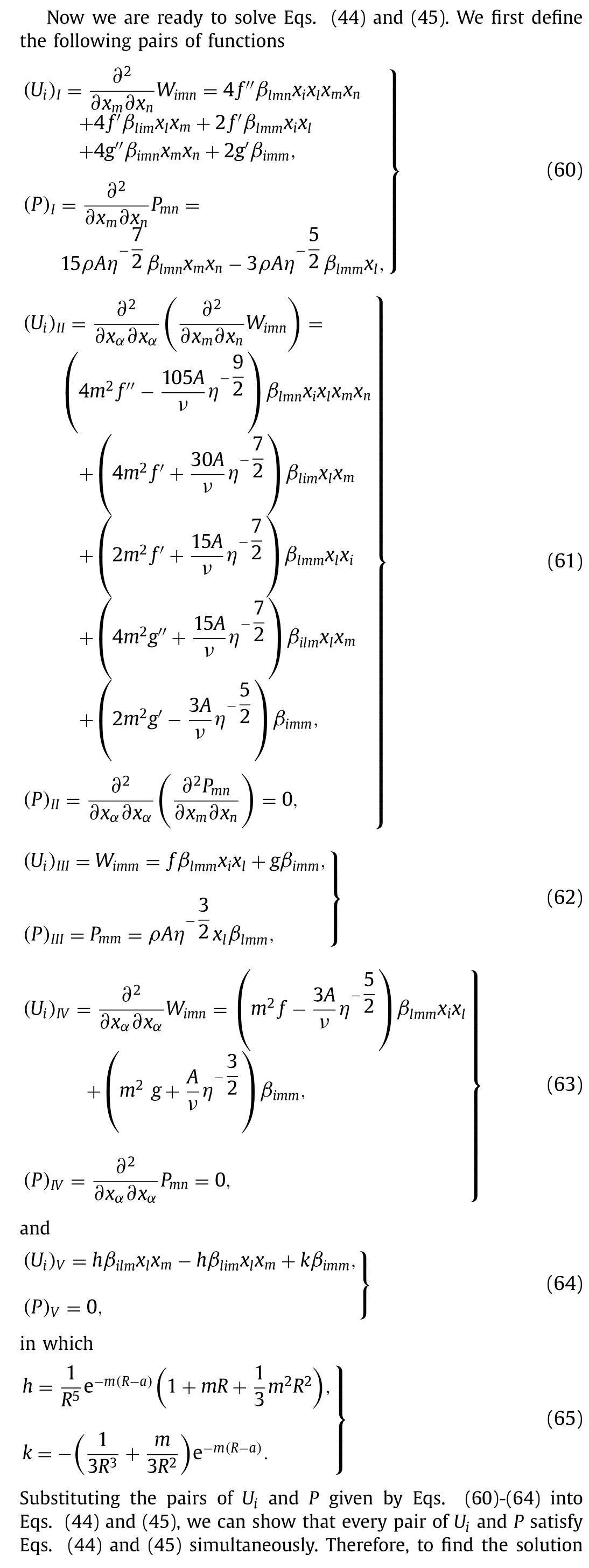


3. Discussion
In the derivation above, we assumed that the velocity of the fluid relative to the center of the sphere is small, which allowed us to neglect the nonlinear terms in the momentum equations. For sand particles suspended in real rivers, this assumption is acceptable. For example, the average diameter of suspending sand particles in the Yellow river is around 0.03 mm. The sedimentation velocity of a sand particle of such size in water due to gravity is very small. Moreover, the inertial effects of such fine particles are also small, thus the particles shall not fall much behind the water flow due to the inertial effects. Taken these two reasons together,the nonlinear terms can be neglected. On the other hand, for sand particles moving along the river bed, which are usually of diameters above 0.2 mm, their relative velocities with respect to the water are much larger, thus the assumption we made above is not applicable.
In the discussion, we also assumed that the length scale of the flow is much larger than the diameter of the sand particles. In rivers, the length scale of the flow is roughly of the same order of the water depth, which is typically a few centimeters to a few meters, indeed much larger than 0.03 mm.
In the derivation, we applied the initial conditionWi=0, which,strictly speaking, is rather arbitrary. On the other hand, what we are interested in is not the exact flow field at early times, but the flow at largert. For the viscous flow around the sphere, the influence of the initial condition disappears quickly astincreases.Therefore, from a practical viewpoint, the arbitrary choice of the initial conditionWi=0 has negligible effects.
Finally, I sincerely thank my supervisor, Prof. Pei-Yuan Chou, for the education and advices that I received from him.
Declaration of Competing InterestThe authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
 Theoretical & Applied Mechanics Letters2022年6期
Theoretical & Applied Mechanics Letters2022年6期
- Theoretical & Applied Mechanics Letters的其它文章
- Influence of physical parameters on the collapse of a spherical bubble
- Shapes of the fastest fish and optimal underwater and floating hulls
- Determination of the full-field stress and displacement using photoelasticity and sampling moiré method in a 3D-printed model
- Constitutive modeling of particle reinforced rubber-like materials
- Predicting solutions of the Lotka-Volterra equation using hybrid deep network
- Numerical simulation of laser ultrasonic detection of the surface microdefects on laser powder bed fusion additive manufactured 316L stainless steel
