Predicting solutions of the Lotka-Volterra equation using hybrid deep network

Zi-Fei Lin, Yn-Ming Ling, Ji-Li Zho, Jio-Rui Li

a School of Statistics, Xi’an University of Finance and Economics, Xi’an 710100, China

b China (Xi’an) Institute for Silk Road Research, Xi’an 710100, China

Keywords:Lotka-Volterra equations HDN-LV algorithm Stochastic Lotka-Volterra equations Parameter optimization

ABSTRACT Prediction of Lotka-Volterra equations has always been a complex problem due to their dynamic properties. In this paper, we present an algorithm for predicting the Lotka-Volterra equation and investigate the prediction for both the original system and the system driven by noise. This demonstrates that deep learning can be applied in dynamics of population. This is the first study that uses deep learning algorithms to predict Lotka-Volterra equations. Several numerical examples are presented to illustrate the performances of the proposed algorithm, including Predator nonlinear breeding and prey competition systems, one prey and two predator competition systems, and their respective systems. All the results suggest that the proposed algorithm is feasible and effective for predicting Lotka-Volterra equations. Furthermore, the influence of the optimizer on the algorithm is discussed in detail. These results indicate that the performance of the machine learning technique can be improved by constructing the neural networks appropriately.

Recently, big data has developed rapidly, and data-based deep learning algorithms have been widely used, from text translation and information recognition to predicting stock prices and disease spread. The results predicted by this method are obtained by using a neural network algorithm with multiple hidden neural states [1].These hidden neural states form a "black box" model with trained internal parameters. We only observe the final model output when given a set of measured training data [2]. For the parameters in the model, time series data is usually used for training, which means that the prediction object of the deep learning model is usually time series data. Time series data in real situations, such as financial data, environmental data, meteorological data, etc., are chaotic. In the mathematical description, we call it chaotic motion.A chaotic time series is generated by the deterministic dynamics of a nonlinear system, which is sensitive to initial conditions and is challenging to predict for such systems. Most scholars use mathematical methods to predict it; these methods can predict accurately in theory. However, they cannot consider future development and change laws and development levels of market phenomena when they make actual predictions. There will be a large deviation when there is a large change in the outside world. Therefore,traditional statistical techniques cannot give reliable predictions for nonlinear dynamical systems.

Machine learning has good results in the prediction of dynamic systems. Scholars have carried out research in this field. Combining machine learning with knowledge-based modeling, LeCun et al.[1] predicted predictions for large, complex spatiotemporal systems. Testing with the Kuramoto–Sivashinsky equation confirms that the proposed method not only can be scaled to provide excellent performance for very large systems, but the time-series data length required to train multiple parallel machine learning components is significantly lower than without parallelization desired length. Wang et al. [3] proposed to predict chaotic dynamics using a neural network with an inhibitory mechanism, and the accuracy of the proposed algorithm was confirmed by simulating a well-known nonlinear dynamical system prototype. And it has been proved that the algorithm is also suitable for predicting the partial differential system. Pyragas and Pyragas [4] used reservoir computing algorithms to predict and prevent extreme events.They used FitzHugh-Nagumo systems as an example to demonstrate the feasibility of the proposed method, with excellent results. Pathak et al. [5] also used the reservoir calculation algorithm to predict the chaotic dynamic system. They confirmed that the proposed method is accurate in short-term predictions by the Lorenz system and Kuramoto-Sivashinsky equations. At the same time, the predicted results can perfectly restore the dynamic characteristics of the original system. Vlachas et al. [6] propose complex spatiotemporal dynamics prediction using a backpropagation algorithm and reservoir computing in recurrent neural networks.They found that when the whole state dynamics are available for training, the RC algorithm outperforms the BPTT method in predicting performance and capturing long-term statistics while requiring less training time. Nevertheless, large-scale RC models can be unstable and more likely to diverge than BPTT algorithms in the case of reduced-order data. In contrast, the neural network trained by BPTT has superior predictive ability. It can well capture the conclusion of the dynamics of low-order systems, which once again confirms the applicability of deep learning in predicting chaotic systems. Cui et al. [7] applied complex network theory to construct echo-state network dynamic reservoirs. They proposed three echo-state networks with different dynamic reservoir topologies. They conducted simulation experiments and detailed analysis and found that the proposed echo state network has higher prediction accuracy and enhanced echo characteristics but still has the same short-term storage capacity. Falahian et al. [8] proposed using a multilayer feedforward neural network to predict some wellknown chaotic systems while evaluating the accuracy and robustness of the model, and the results proved reliable. Besides, they utilize the proposed neural network to represent the modeling results of this chaotic response model. The ability of the neural network to simulate this specific brain response was demonstrated.Follmann and Rosa [9] used reservoir computational algorithms to predict the temporal evolution of neuronal activity resulting from the Hindmarsh-Rose neuron model. Accurate short- and longterm predictions of cyclical (tonic and explosive) neuronal behavior were obtained, but only accurate short-term predictions of chaotic neuronal states. However, the studies mentioned above all stay in biology and meteorology but do not involve population dynamics.Population dynamics are fundamental to our lives.No population in nature is isolated; any complex ecosystem is a complex network formed by the interaction of multiple populations, such as intraspecies competition, cooperation, interspecies predation, and predation.

This paper proposes a deep hybrid neural network for predatorprey model prediction. We predict nonlinear predator reproduction and prey competition systems, predator nonlinear predator reproduction and prey competition stochastic systems, and one-prey and two-predator competition systems, respectively, and find that the proposed algorithm, compared with traditional neural network algorithms, can Improve prediction accuracy. At the same time, for the dynamic characteristics of the system, the results predicted by the algorithm can also be perfectly reproduced. In addition, we also discuss the algorithm’s more interesting issue: the optimizer’s choice.

The Lotka-Volterra equation is a dynamical system consisting of two first-order nonlinear differential equations, also called the predator-prey equation, proposed by Lotka and Volterra in 1296[10–12]. It is often used to describe the dynamics of predators in biological systems as they interact with their prey. Specifically,the size of the two populations waxes and wanes. The dynamical model that can describe the size of the two populations was initially proposed as

Fig. 1. Convolutional neural network.

In Eq. (2), all terms are replaced by the corresponding population density functions. WhereB(x,y)represents the rate at which the prey is consumed, i.e., the predation rate, it is a monotonic non-decreasing function that depends on the population density of predators and prey.D(x,y)is called the fertility function and represents the reproductive rate of the predator. In the original expression, we considered that the relationship between the biomass of the prey and the biomass of the predator is constant; keeping this assumption and considering other additional factors, the formD(x,y)is formed.A(x)represents the reproduction of the prey itself, andC(y)represents the reproduction of the predator itself.

Convolutional neural networks are a class of feedforward neural networks that include convolutional computation and have a deep structure, and are one of the representative algorithms of deep learning. Research on it began in the 1980s and 1990s, with timedelay networks and LeNet-5 being the first convolutional neural networks to appear [13]. After the twenty-first century, with the proposed deep learning theory and the improvement of numerical computing devices, convolutional neural networks have been developed rapidly and applied to computer vision, natural language processing, and other fields [14]. It differs from an ordinary neural network by including a feature extractor consisting of a convolutional layer and a subsampling layer (pooling layer). In the convolutional layer of a convolutional neural network, a neuron is connected to only some of the neighboring neurons and usually contains several feature maps; each feature map consists of several rectangularly arranged neurons, and the neurons of the same feature map share weights, where the shared weights are the convolutional kernel. For subsampling (pooling), there are usually two forms of mean pooling and max pooling, which can be regarded as a unique convolution process. Convolution and subsampling greatly simplify model complexity and reduce model parameters. In order to get the output feature mapY, we use the convolution kernelsW1,W2,...,Wpto convolve the input feature mapsX1,X2,...,Xnrespectively, then add the convolution results and add the upper bias termb, the net inputzof the convolution layer is obtained, and the output feature mapYis obtained by performing a nonlinear transformation on it. After the convolutional layer operation is performed, the obtained feature mapYis used for feature selection to reduce the number of features, thereby reducing the number of parameters and preventing overfitting. Figure 1 shows the exact mechanism of operation of the algorithm.

Fig. 2. Gated recurrent units neural network.

The traditional recurrent neural network has some shortcomings that are difficult to overcome. One of the biggest problems is gradient disappearance and gradient explosion [15–17]. To solve these problems and improve prediction accuracy, Cho [18] proposed a gated recurrent unit neural network (GRU) in 2014. GRU proposes using two vectors, the update gate. It resets the gate to decide what information should be passed to the output. It can save information from a long time ago and remove irrelevant information, enhancing the neural network’s memory capacity and making the final classification and regression more accurate. The update gate controls how much state information from the previous moment is brought into the current state. The larger the value,the more state information from the previous moment is brought in; the reset gate controls how much state information from the previous moment is ignored. The smaller the value, the more it is ignored. From Fig. 2,Z(t)represents the update gate, which acts similarly to the forgetting and input gates in the LSTM algorithm,deciding what information to discard and what new information to add.Rtis the reset gate, the reset gate is used to decide the degree of discarding the previous information, andH(v)is the final predicted time series data result. Equations (3)–(6) illustrates how the GRU are calculated, whereWrepresents the weight.

In cognitive science, due to bottlenecks in information processing, humans selectively focus on a portion of all information while ignoring other visible information. The above mechanism is often referred to as the attention mechanism. For a classification task,we extract image features and classify the images into different classes based on the differences between these features. However,only useful features contribute to the classification, while different features have different meanings [19–21]. The method has been widely used in text recognition and image recognition. It has been confirmed that it is effective in extracting features.

Figure 3 is the input data, which is passed to the softmax layer by Eq. (7) to obtain the attention distribution, let it be, which can be interpreted as the degree of attention of the message. Then pass through Eq. (8) to finally get the required informationa.We introduced some basic algorithms of neural networks, which can obtain prediction results but are limited by their respective drawbacks, and the accuracy of the obtained prediction results is often poor. We will describe the numerical scheme for predicting the Lotka-Volterra equation by deep neural networks and name it the HDN-LV algorithm.

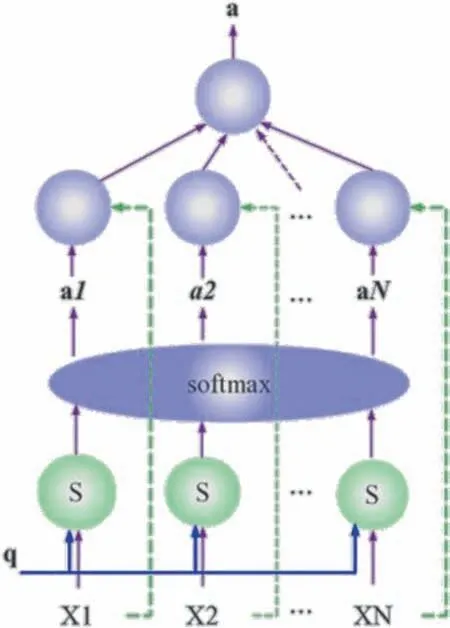
Fig. 3. Attentional mechanism.

We propose a form of neural network connectivity. We use a layer of two-dimensional convolutional neural network and a layer of attention mechanism for feature extraction of the features present in the original data. We finally pass them to the traditional DNN fully connected layer to produce the final output. Next, the GRU model trains and predicts the output data to achieve better prediction results. In addition, we introduce a regularization factor as a penalty term in the algorithm to achieve higher prediction accuracy.

We will construct the HDN-LV algorithm. For the selection of the prediction range, the range of the independent variables of the Lotka-Volterra equation needs to be truncated since the prediction range of the deep hybrid neural network should be a finite set.Considering that in practice, the usual forecasts often do not require particularly long periods, we should choose a suitable interval. According to the literature [22], it is known that the currently obtained prediction horizon is about 5 to 6 Lyapunov times, where one Lyapunov time is the reciprocal of the maximum Lyapunov exponent. So we calculate the Lyapunov exponent for the system’s initial solution to determine the prediction’s final interval.

Algorithm 1 is the implemental process of the proposed HDNLV algorithm, and four different systems will be given to test the validity of our method in the next step.

Then we select predator nonlinear reproduction prey competition systems, one prey and two predator competition systems, and stochastic systems with noise added to confirm that HDN-LV methods can predict the dynamical evolution of ecosystems.

Algorithm 1 HDN-LV algorithm.

Fig. 4. Numerical solution of predator nonlinear reproduction and prey competition system.

Based on the numerical solution, we calculate the largest Lyapunov exponent for Eq. (10) as 0.1771. Therefore, the prediction time is chosen as [0,200]. We set the penalty factor of the algorithm to 6×10−4. The size of the network is set to four hidden layers with 80 nodes in each hidden layer. Meanwhile, the Adam optimization technique is applied, getting the minimum value of the loss function is about 10−6. Figure 5 and Table 1 show the obtained results. The blue dashed line is the HDN-LV solution, and the 10–6green dashed line is the GRU solution. Compared to the conventional GRU algorithm, the solution of the HDN-LV algorithm is almost identical to the numerical solution marked by the solid red line, with an average accuracy of 99.98%. These results show that the HDN-LV method effectively predicts the Lotka-Volterra equation.

We investigated the predicted dynamical characteristics of predator nonlinear reproduction and prey competition systems,and the results were ideal. However, the study of this situation alone does not exactly match the reality. In real life, the system may also be affected by factors other than predators and prey, such as weather changes, earthquakes, tsunamis, floods, other natural disturbances, and human interference. In this part, we add random noise to Eq. (10) to confirm the efficiency of the HDN-LV algorithm.We establish the Ito equation for Eq. (14) [23].

whereσu1,σv1is the noise intensity anddwu,dwvis the standard Wiener process, setσu1=σv1=0.1. The training data of the algorithm is obtained by iterating on Eq. (14) using the fourth-order Runge-Kutta method with the initial values as shown in Fig. 6.

The prediction interval is also determined by calculating the largest Lyapunov exponent. According to the calculation results,the final prediction interval is [0,180]. Using the HDNN-LV algorithm, the activation function is selected as thetanh function, the loss function is minimized using the Adam method, and the minimum loss value is about 10−6. Where, we set the penalty factor of the algorithm to 1×10−3. Meanwhile, the conventional GRU algorithm is designed to be compared with the HDN-LV algorithm.From Fig. 7a and 7b, it can be seen that the results obtained bythe HDN-LV algorithm prediction are closer to the stochastic solution compared to the traditional GRU algorithm. Meanwhile, from Fig. 7c and 7d, we can see that the absolute error of the HDN-LV algorithm is closer to zero than the GRU algorithm’s absolute error. To confirm the prediction, we calculated the largest Lyapunov exponent. FromTable 2, it can be seen that the largest Lyapunov exponent calculated by the prediction results of the HDN-LV algorithm is closer to the largest Lyapunov exponent calculated by the stochastic solution. This illustrates that the results predicted by the HDN-LV algorithm fit the stochastic solution more closely,both numerically and in terms of kinetic characteristics, which also shows that the HDN-LV algorithm is more effective in predicting the Lotka-Volterra equation.

Table 1 The accuracy of the HDN-LV method for Eq. (10).

Fig. 5. The comparison results between the solution obtained from the HDN-LV algorithm, GRU algorithm, and the exact solution. The blue dashed line is the HDN-LV solution, the green dashed line is the GRU solution, and the solid red line is the exact solution.

Fig. 6. Stochastic solutions of predator nonlinear reproduction competes with prey.

Fig. 7. (a) and (b): The comparison results between the solution obtained from the HDN-LV algorithm, GRU algorithm, and the stochastic solution. The blue dashed line is the HDN-LV solution, the green dashed line is the GRU solution, and the solid red line is the stochastic solution. (c): Absolute error of HDN-LV algorithm and GRU algorithm. Green represents the absolute error of the HDN-LV algorithm, and yellow represents the absolute error of the GRU algorithm.

Table 2 Largest Lyapunov exponent.

Fig. 8. Numerical solution phase diagram of a competitive system of one prey and two predators: (a) Prey-predator1 projection; (b) Prey-predator2 projection; (c)Predator1-predator2 projection.

Fig. 9. (a) and (c): The comparison results between the solution obtained from the HDN-LV algorithm, GRU algorithm, and the numerical solution. The blue dashed line is the HDN-LV solution, the green dashed line is the GRU solution, and the solid red line is the numerical solution. (d): Absolute error of HDN-LV algorithm and GRU algorithm. Green represents the absolute error of the HDN-LV algorithm, and yellow represents the absolute error of the GRU algorithm.

Fig. 10. Stochastic solution of the competitive system of one prey and two predators.

For the initial value of Eq. (16). Setu=1,v1=1,v2=1,γ1=10,γ2=10,α=0.31,β=0.29, assuming the same initial density of predator and prey, and iterate using the fourth-order Runge-Kutta method. Thus determine what happens to the system after it evolves.

From Fig. 8, the population density of predator1 decreases dramatically after a short period and eventually remains flat around zero. This is due to the competition this predator received from another predator and its influence. At the same time, Predator2 showed a wide range of oscillations in the initial period untilt=6.5, when the density of this population stabilized, fluctuating around 0.8. This indicates that after the initial experience of competition between predator populations, the population is more adapted to the current environment compared to the other predators and reaches equilibrium after getting some depletion. For prey,the same large oscillation experienced in the initial period was caused by competition between the two predator populations. The eventual increase in prey due to the decrease in predator1 led to the eventual stabilization of population density fluctuating around 1.8after the initial oscillation. We use the proposed HDN-LV algorithm for prediction.

We set the prediction interval to be [0,200]. Using the Adam optimization algorithm, the loss function is minimized by subiterations. The results are shown in Fig. 9a–9c. Here, we set the penalty factor of the algorithm to 5×10−6. The HDN-LV method is used to solve Eq. (16) by setting the network with four hidden layers and 50 nodes in each hidden layer. The maximum absolute error between the HDN-LV and the exact solutions is 10–3.The prediction effect can be seen more intuitively in Fig. 9. Compared with the other traditional algorithm, the prediction effect of the HDN-LV algorithm is better. Its prediction accuracy is 99.91%, the highest among the three methods.

Fig. 11. (a) and (c): The comparison results between the solution obtained from the HDN-LV algorithm, GRU algorithm, and the numerical solution. The solid blue line is the HDN-LV solution, the green dashed line is the GRU solution, and the solid red line is the numerical solution. (d)-(f): Absolute error of HDN-LV algorithm and GRU algorithm. Blue represents the absolute error of the HDN-LV algorithm, and the green represents the absolute error of the GRU algorithm.

Table 3 The comparison of Adam and Adam-decay optimizer in the 2D case.

Table 4 The comparison of Adam and Adam-decay optimizer in the 3D case.

Meanwhile, the training time is 1651 s when using the HDN-LV method. In comparison, the conventional GRU algorithm takes the 2540 s, and the accuracy of our proposed method is higher than that of the conventional method. This shows that the initial features we designed to extract the data are practical to obtain more accurate prediction results and improve computational efficiency.

We add random noise to the 3D Lotka-Volterra equation to determine the proposed method’s validity. For Eq. (16), establish the corresponding Ito equation to obtain Eq. (17) [22].

whereσu,σv1,σv2is the noise intensity anddwu,dwv1,dwv2is the standard Wiener process. Setσu=σv1=σv2=0.1 and iterate on Eq. (17) using the fourth-order Runge-Kutta method to obtain the training data for the algorithm with the initial values as shown in Fig. 10.

Using the HDN-LV method, we predicted Eq. (17). The predicted interval is [0,190]. For step 1, we choose a training set size of 2000.In step 2, we consider a network with eight hidden layers and 40 nodes in each hidden layer and set the penalty factor to 8×10−4.The weights of the initial algorithm and the deviations are optimized using the Adam optimization algorithm, and the results as shown.

From Fig. 11a–11c, it can be found that the results obtained by the HDN-LV algorithm are closer to the initial value compared to the other traditional algorithm, where the training loss is about 10−7. The absolute error of the system is shown in Fig. 11d–11f,which clearly shows that the calculation results obtained by the proposed method are closer to zero compared with other algorithms, which is also a side indication of the accuracy and effectiveness of the algorithm.

In this paper, we propose the HDN-LV algorithm and confirm that it can obtain high accuracy by predicting the Lotka-Volterra equation and the stochastic Lotka-Volterra equation. In this part,we discuss the questions about it: how the optimizer is selected to be used to train the HDN-LV algorithm.

We optimize the initial algorithm using the Adam optimizer and find that it achieves satisfactory training results only when iterations reach 2×104, which can lead to long training times and cannot get the desired accurate answers fast enough. Therefore, we tried to improve the optimizer. We found it very effective to continue adding decay rate metrics to the Adam optimizer instead of using the adaptive form. We compared the prediction results of the conventional Adam and Adam methods by adding the decay rate index in the two-dimensional and three-dimensional cases. The results are shown in Tables 3 and 4.

We set the same prediction interval as the traditional method and the parameters of the initial algorithm and use the same computer for its calculation. It can be found that the Adam algorithm with an increased decay rate significantly improved computational efficiency, ensuring that the computation can be completed within 1000 s. In addition, the accuracy of Adam’s method with an increased decay rate is higher than that of traditional optimization methods. Therefore, artificially increasing the decay rate for the Adam method can achieve the same or even better results than the traditional Adam method and save time.

This paper proposes an HDN-LV method for predicting the Lotka-Volterra equation using deep learning methods. Two examples of 2D and 3D Lotka-Volterra equations and their stochastic forms show that the proposed HDN-LV algorithm has high accuracy. Compared with traditional methods, the method proposed in this paper does not require a deep mathematical foundation. It does not require any transformation of the equations. At the same time, the short computation time and high accuracy are also advantages. Meanwhile, we introduce a regularization factor as the penalty term of the neural network to avoid the initial algorithm overfitting affecting the prediction accuracy.

In addition, we discuss the selection of the optimizer and the setting of the penalty factor in the HDN-LV method. For the selection of the optimizer, we found that for the adaptive Adam optimizer, setting the decay rate index for it can get the desired prediction results more quickly under the condition of guaranteeing the prediction accuracy.

It should be noted that while the HDN-LV method is effective for predicting Lotka-Volterra equations driven by white noise,the prediction effectiveness of using this method for other cases,such as color noise-driven Lotka-Volterra equations and broadband and narrowband noise-driven Lotka-Volterra equations, is unknown. Therefore, higher performance and better storage capacity are required to improve the prediction accuracy when solving dynamic systems driven by color noise and wide-band and narrowband noise.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgment

The research was supported by the National Natural Science Foundation of China (No. 11902234), Natural Science Basic Research Program of Shaanxi (No. 2020JQ-853), China (Xi’an) Silk Road Research Institute Scientific Research Project (No. 2019ZD02),Shaanxi Provincial Department of Education Youth Innovation Team Scientific Research Project (No. 22JP025), and the Young Talents Development Support Program of Xi’an University of Finance and Economics.