考虑微观界面的2D 编织SiC/SiC 复合材料宏-细-微多尺度渐进损伤失效分析

张 力，王 猛，陈 强,3，李彦斌,3，皮慧龙，董萼良

(1. 东南大学空天机械动力学研究所，江苏，南京 211189；2. 东南大学工程力学系，江苏，南京 211189；3. 东南大学机械工程学院，江苏，南京 211189；4. 北京空天技术研究所，北京 100074)

陶瓷基复合材料具有耐高温、比强度高、比模量高等优点。其中，SiC/SiC 复合材料由于纤维与基体具有相近的热膨胀系数，可以极大的改善材料制备过程中的热变形失配问题，目前已被广泛用于航空航天飞行器中。但实际工程中，SiC/SiC复合材料面临严重的损伤和失效问题。

使用宏观失效准则可以较为简便地预测复合材料强度。王成华等[1]基于Tsai-Wu 准则提出了一种新型刚度退化模型，建立了一套复合材料结构渐近损伤失效分析方法。相超等[2]采用Hashin准则进行了拉伸荷载下贴补复合材料层合板的渐近损伤失效分析。古兴瑾等[3]采用Hashin 准则和Quads 判据进行了复合材料层板损伤分析。朱炜垚等[4]采用Yamada-Sun 准则建立了含低俗冲击损伤复合材料层合板压-压疲劳寿命预测模型。庄茁等[5]采用不同宏观失效准则对复合材料冲击损伤，含缺陷结构极限强度进行了研究。采用宏观失效准则虽然能预测复合材料强度，但却无法揭示复合材料细、微观损伤失效过程和失效机理。为解决上述问题，多尺度方法被广泛用于复合材料等效参数预测和损伤失效分析中。

多尺度分析方法通过建立不同尺度模型之间的联系对复合材料力学性能进行分析。Hui 等[6]采用分等级多尺度方法，通过对微观单胞模型施加周期性边界条件[7]预测纤维束等效参数，并从细、微观尺度揭示了SiC/SiC 复合材料的渐进损伤失效过程。石多奇等[8]采用考虑三相的混合率公式计算纤维束等效弹性参数，研究了含孔隙三维编织复合材料的弹性参数。费庆国等[9]和陈素芳等[10]采用分等级多尺度方法研究了复合材料高温环境下的等效参数。金浏等[11-12]基于分等级多尺度方法，将轻骨料混凝土视为一种三相复合材料，建立其细观数值模型进行分析。Wang 等[13]采用分等级多尺度方法研究了考虑热残余应力情况下，孔隙对单向复合材料横向力学性能的影响。Huang 等[14]采用分等级多尺度方法研究了含孔隙3D 编织复合材料弹性力学性能。田志强等[15]基于子模型插值方法建立宏-细观模型之间的联系，进行了复合材料层合板四点弯工况下的损伤分析。熊波等[16]采用多尺度有限元思想，将精细化的接头模型嵌入宏观桁架模型中，对全复合材料桁架进行了分析。Bednarcyk 等[17]采用通用单胞模型与复合材料宏观模型相结合的方法进行了复合材料结构的多尺度分析，分析了温度和基体材料粘弹性对单向复合材料层合板冲击力学性能的影响。Borkowski 等[18]在细、微观尺度上均采用通用单胞模型，进行了陶瓷基编织复合材料的多尺度分析。张博明等[19-20]采用通用单胞模型研究了复合材料的损伤失效过程。李星等[21]采用基于微观失效理论的多尺度方法，通过放大因子进行宏观应力到细观应力之间的信息转换，建立了一种基于物理失效模式的复合材料跨尺度失效准则。Liu 等[22]采用此方法，研究了考虑材料温度效应的开孔单向复合材料板在压缩荷载下的损伤过程。Wang 等[23-24]采用此方法研究了复合材料热压罐在不同荷载下的损伤失效过程。Liao 等[25]采用此方法分析了单向复合材料层合板在冲击荷载下的损伤失效行为。Chowdhury等[26]分析了编织复合材料结构在弯曲荷载作用下的损伤失效过程。Xu 等[27]采用此方法预测了两种不同材料体系编织复合材料的强度。Wang 等[28]提出了一种采用k-means 聚类分析[29]，通过缩聚后的低阶尺度模型代替原本的精细低阶尺度模型的方法并提取每个聚类的放大因子，从而基于微观力学失效理论分析了编织复合材料单胞模型在拉伸和压缩荷载下的损伤失效过程。在此基础上，王猛[30]针对细、微观单胞模型都采用聚类方法进行缩聚，并基于编织复合材料子单胞模型[31-33]，采用通用单胞模型理论[34]，结合将2D编织结构简化为0°/90°铺层结构的思想[35]，发展了一种编织复合材料等效弹性预测方法，从而实现了跨越宏-细-微三个尺度的多尺度损伤失效分析。但在上述研究中，微观纤维与基体间的界面(即微观界面)未被纳入宏-细-微三个尺度的多尺度分析过程中，因此无法在分析宏观模型损伤失效过程时考虑微观界面的影响。已有试验研究[36-37]表明：陶瓷基复合材料拉伸破坏时，界面脱粘是引起材料破坏的主要失效模式之一，沿拉伸方向材料首先出现界面的脱粘，而后脱粘的纤维成簇拔出。因此，在分析陶瓷基复合材料损伤失效过程时，微观界面组分不可忽略。

本文将微观界面组分纳入宏-细-微三个尺度的多尺度渐进损伤失效分析中，采用缩聚的放大因子进行多尺度信息传递，并结合细、微观复合材料失效理论与编织复合材料等效参数计算方法，进行了2D 编织SiC/SiC 复合材料宏-细-微多尺度渐进损伤失效分析。首先对细、微观单胞模型施加周期性边界条件获取每个单元的放大因子，采用k-means 聚类分析方法，对放大因子进行缩聚，通过缩聚的放大因子进行多尺度信息传递。进而，结合细、微观失效理论进行损伤失效判定并计算等效损伤变量，获取各组分退化后的弹性参数。采用混合率公式与均匀化方法计算纤维束等效弹性参数。基于编织复合材料通用单胞模型理论计算宏观模型损伤后的等效弹性参数。然后，通过不同聚类数目的计算结果对比证明了所采用聚类数目的正确性，并研究了微观界面对材料强度计算结果的影响。同时，从宏-细-微三个尺度分析了材料的损伤失效过程。

1 多尺度分析模型

图1 为多尺度分析有限元模型，表1 为微观单胞模型不同组分材料参数，表2、表3 对应图1(a)、图1(b)中细、微观单胞模型尺寸。

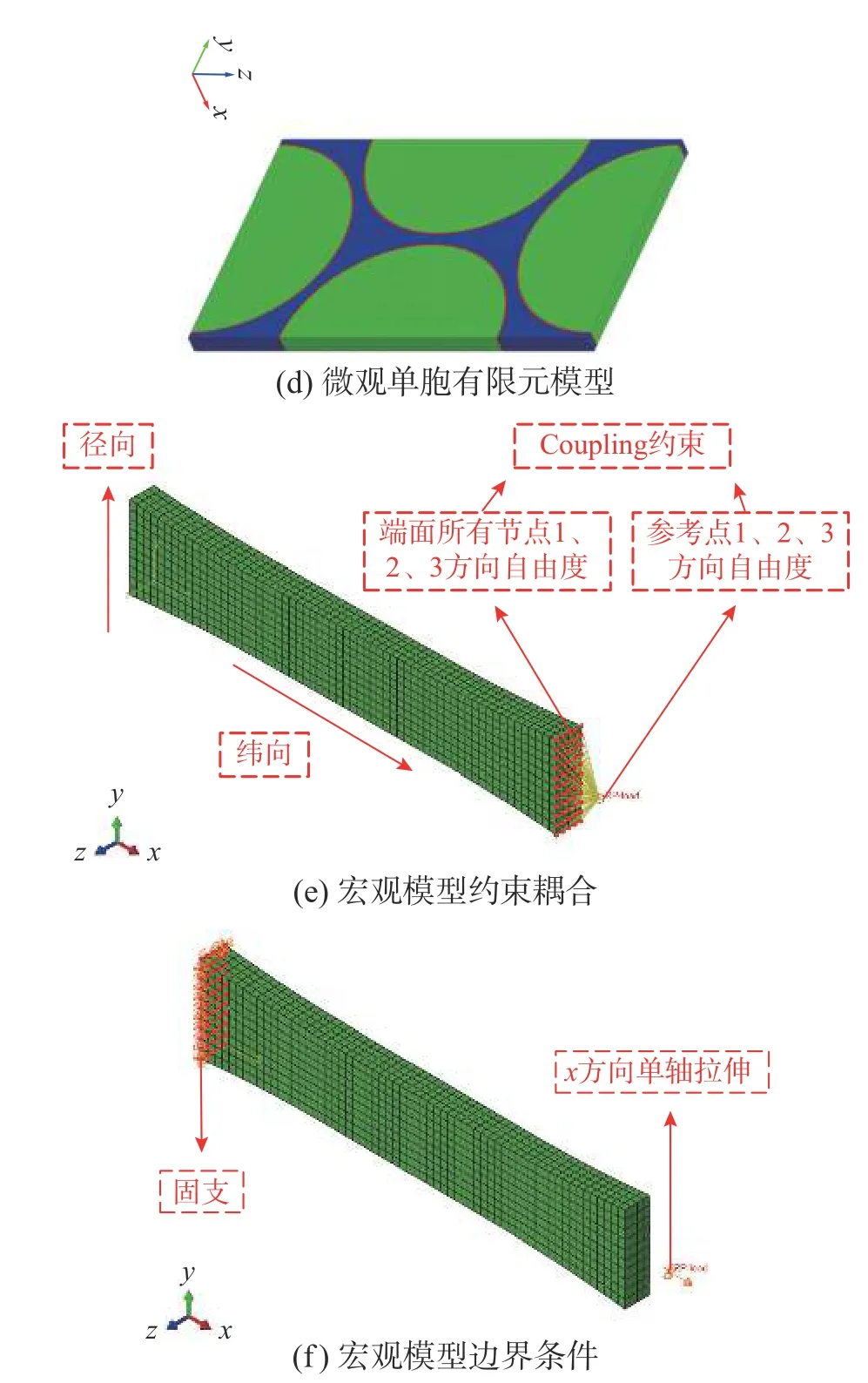
图1 多尺度分析有限元模型Fig. 1 Finite element model of multiscale analysis

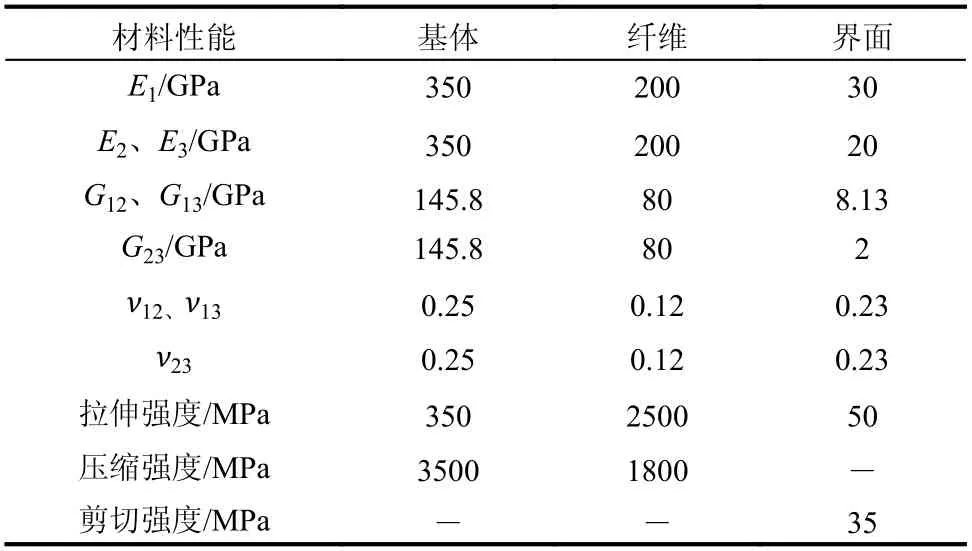
表1 材料参数[6]Table 1 Material parameters[6]

表2 细观单胞模型尺寸参数[6]Table 2 Size parameters of mesoscale cell model[6]

表3 微观单胞模型尺寸参数[6]Table 3 Size parameters of microscale cell model[6]

宏观模型如图1(e)、图1(f)所示。在对宏观模型进行分析时，将一侧端面所有节点固支，另一侧端面所有节点的1、2、3 方向自由度通过Coupling约束与参考点自由度耦合，从而便于拉伸荷载施加和提取荷载信息。通过对参考点施加位移，使宏观模型产生2.1 µε 的变形。

2 多尺度信息传递方法

对细、微观单胞进行分析获取放大因子[29]，如式(1)所示，其展开形式如式(2)所示。

通过该放大因子即可将高阶尺度模型的应变信息传递至低阶尺度模型，并计算得到低阶尺度模型的应力状态，从而可进行后续的损伤失效分析。

获取放大因子的详细步骤为：首先给单胞模型施加周期性边界条件[7]，依次令的某一项为1，其余项为0，输出每个单元的应力状态。之后将每个单元在6 种周期性边界条件下得到的应力向量按列排列即得到该单元的应变-应力放大因子。

若直接采用细、微观单胞每个单元的放大因子进行多尺度分析，计算量会十分巨大。此处采用k-means 聚类分析方法[28-30]，将具有相似力学行为的单元划为一类，采用每个类内单元的放大因子平均值作为该类单元的放大因子，从而减少计算量。

得到每个单元的应变-应力放大因子后，将每个单元放大因子排列为式(3)所示的1×36 的向量。

对所有需要聚类的单元采用k-means 聚类分析方法进行聚类。k-means 聚类分析方法目标是在将所有单元分为k个类后(S={S1,S2, ···,Sk})，每个类中的向量距离此类平均值的距离之和最小，如式(4)所示：

之后计算每个类内单元的放大因子平均值，并用于宏观模型的分析中。

对于细观纯基体、微观尺度所有组分获取的是应变-应力放大因子，而纤维束获取的是应变放大因子。获取应变放大因子的过程与获取应变-应力放大因子的过程类似，只需将式(1)左侧的应力向量换为应变向量即可。

3 失效判定准则和损伤扩展模型

获得细、微观组分各聚类应力后，需要进行损伤判断。

细观纯基体、微观基体采用摩尔失效准则，如式(5)所示：

式中：σ1和σ3分别是第一主应力和第三主应力；σta与σca为容许应力，在本文中分别使用基体材料拉伸强度和压缩强度代表容许应力。

微观界面采用最大应力准则，如式(6)所示：

式中：σ1、σ2、σ3为界面材料1、2、3 三个方向的正应力；σ12、σ13、σ23为界面材料12、13、23 三个方向的剪应力；Fij为界面材料不同方向的强度值。本文中，仅考虑界面材料受拉破坏和剪切破坏两种情况，且1、2、3 方向拉伸强度相同，12、13、23 方向剪切强度相同。

微观纤维采用最大主应力准则，如式(7)所示：

式中：σ1为第一主应力；σult为纤维材料强度。当沿第一主应力方向受拉时，σult为拉伸强度，当沿第一主应力方向受压时，σult为压缩强度。

采用上述准则对各聚类进行损伤判断后，如果某聚类发生损伤，引入损伤变量对该聚类的刚度进行退化，如式(8)所示。

式中，D为损伤变量，对于脆性材料，D一般设置为如0.9、0.99、0.999 等一系列的值[22-28]。本文在保证数值计算收敛的前提下，使D的取值尽可能接近于1，参考文献[22 - 28]中的取值，本文将D设置为0.99。

式(8)所示的刚度退化方法与式(9)所示的弹性参数退化方法是等价的。

微观尺度损伤判断后，得到的是微观各组分所有聚类的损伤变量，而计算纤维束等效弹性参数，需要获取微观各组分等效损伤变量。本文采用式(10)的方法计算等效损伤变量，微观纤维与微观界面采用损伤程度最大的聚类对应的损伤变量作为等效损伤变量，微观基体按各聚类在微观基体总体积中的体积含量进行损伤均匀化计算[27]，采用均匀化计算结果作为微观基体等效损伤变量。

通过式(10)的方法计算得到微观各组分等效损伤变量后，采用式(9)的弹性参数退化方法，将D换为式(10)中的等效损伤变量，即可计算得到微观各组分退化后的等效弹性参数。

对于细观纯基体，采用和微观基体类似的计算方法，即首先按式(10)所述的基体损伤均匀化计算方法计算细观纯基体等效损伤变量，只不过将体积含量换为细观纯基体各聚类体积含量即可。之后按照式(9)的弹性参数退化方法计算细观纯基体退化后的弹性参数，仅需将式(9)中的D换为细观纯基体计算得到的等效损伤变量即可。

4 等效弹性参数计算

4.1 纤维束等效弹性参数计算方法

采用考虑三相的混合率公式计算纤维束各聚类等效弹性参数[8]，如式(11)所示。

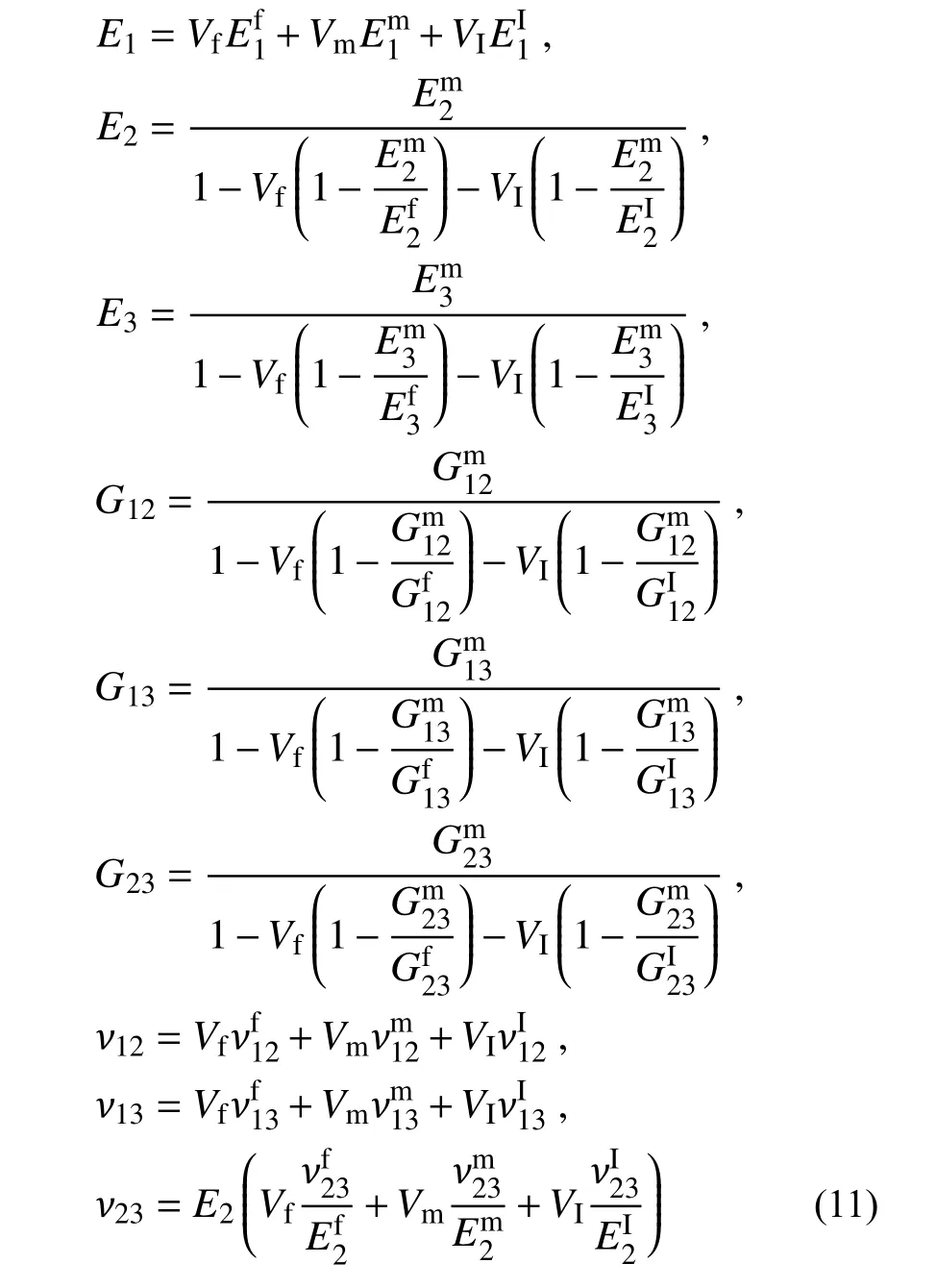
式中：f、m、I 分别为纤维、基体、界面；V为相应组分在微观单胞模型中的体积分数。

得到纤维束各聚类等效弹性参数后，假设纤维束等效弹性参数通过每个纤维束聚类在整个纤维束内的体积含量进行确定，采用式(12)的均匀化方法计算得到纤维束等效弹性参数。

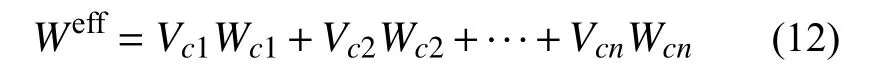
式中：Weff为纤维束的等效弹性参数；Wcn为纤维束第n个聚类的等效弹性参数，包括弹性模量、剪切模量、泊松比等；Vcn为纤维束第n个聚类在对应纤维束中的体积含量。

4.2 编织复合材料等效弹性参数计算方法

获得纤维束、纯基体退化后的等效弹性参数后，基于编织复合材料子单胞模型[31-33]和通用单胞模型理论[34]，可计算得到编织复合材料等效弹性参数[30]。编织复合材料子单胞模型如图2 所示。其中，子单胞模型的纤维束和纯基体体积分数与精细的细观单胞模型体积分数相同。

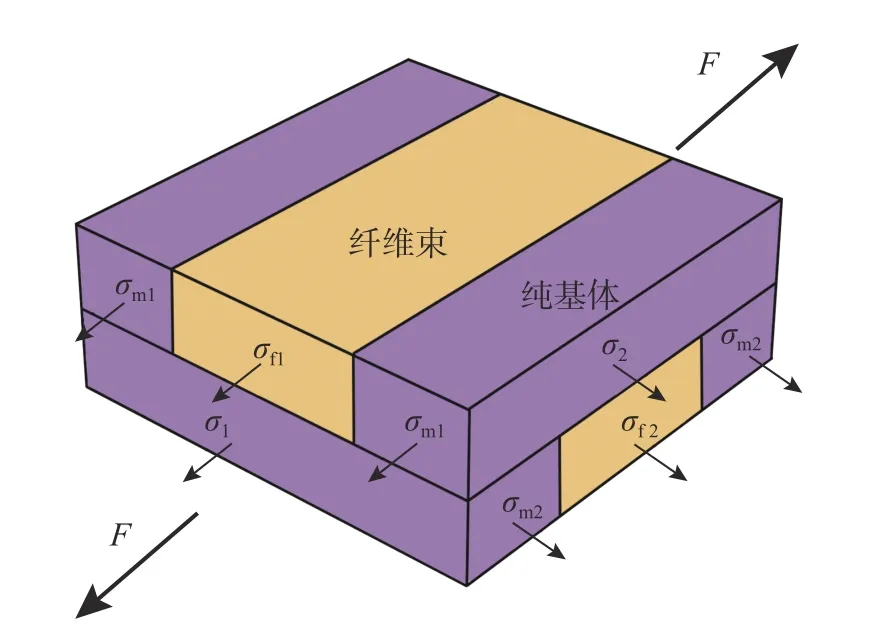
图2 编织复合材料子单胞模型Fig. 2 Sub-unit cell model of braided composites

基于通用单胞模型理论[34]即可计算得到编织复合材料等效参数。采用考虑两相的混合率公式，进一步将上、下两层简化为两个子胞，这两个子胞可以分别看作0°和90°的单向复合材料板[30,35]，简化流程如图3 所示。其中，考虑两相的混合率公式与式(11)类似，只需要把式(11)中界面的部分去除即可。

图3 编织复合材料子单胞模型简化Fig. 3 Sub-unit cell model simplification of braided composites

通用单胞模型假设相邻两个子胞之间是位移和应力连续的，从而建立起外部应力和应变荷载与子胞内应力和应变关系，再结合子胞对应组分材料的本构关系，最终可以建立外部应变荷载和子胞内应变量之间的关系。

首先，分别记上、下两个子胞为子胞α 与子胞β，两个子胞长、宽、高均为Zl、Zw、Zh。两个子胞之间满足式(13)所示的应变连续条件，并可表示为式(14)的矩阵形式。

式中：εs由所有子胞应变组成；为外部应变。

其次，两个子胞相邻面应力满足如式(15)的力平衡条件。结合子胞应力-应变关系，可将式(15)表示为以子胞应变为未知量的矩阵形式，如式(16)所示：

将式(14)与式(16)组装为式(17)的形式：

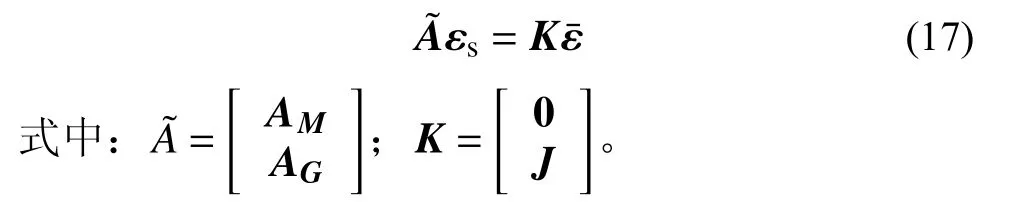
根据式(18)所示外部应力与外部应变之间的关系，并结合式(17)外部应变与子胞应变之间的关系，可以得到子单胞模型等效刚度矩阵表达式，如式(19)所示。最终得到编织复合材料等效弹性参数：

5 多尺度分析流程

将各聚类放大因子用于宏观模型的分析过程中。在宏观模型计算过程每个增量步中，将所有高斯点的应变向量乘以细观放大因子，从而得到细观纯基体各聚类应力与纤维束各聚类应变。再将纤维束各聚类应变乘以微观放大因子，获得微观纤维、基体聚类、界面各聚类的应力向量。结合第3 节失效判定准则及损伤扩展模型，对各组分材料进行损伤失效判断，对于发生损伤的组分进行弹性参数的退化。结合第4 节等效弹性参数计算方法，计算宏观模型退化后的等效弹性参数，并将退化后的等效弹性参数用于下一步计算中。整体流程如图4 所示。此多尺度分析流程通过对商业有限元软件进行二次开发实现。

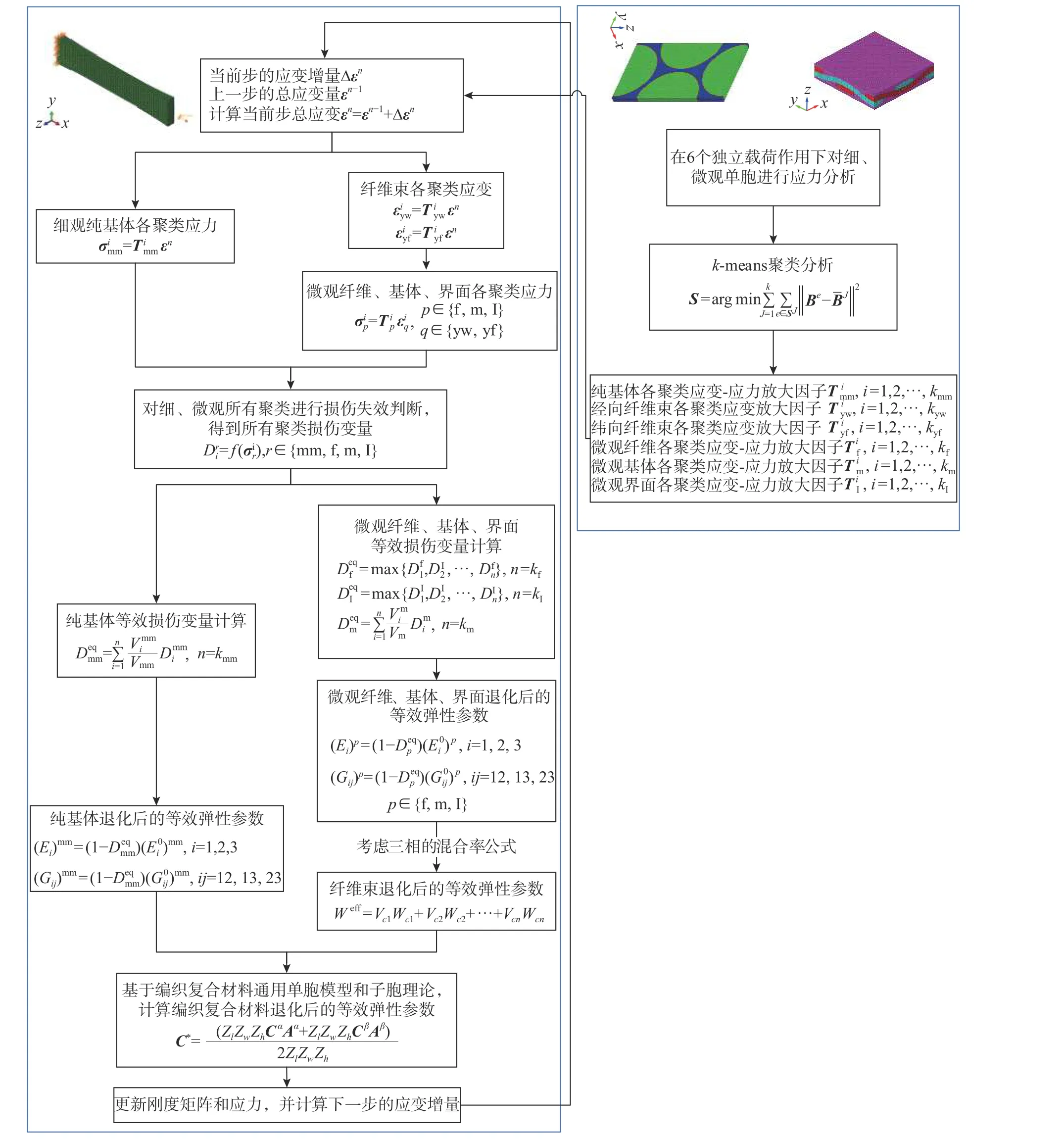
图4 多尺度分析流程图Fig. 4 Flow chart of multiscale analysis

6 聚类数目的影响

根据第2 节的分析，细、微观单胞放大因子的聚类数目会对计算结果造成影响。本节对比3 种不同聚类划分方案，验证了所采用聚类数目的正确性。3 种聚类划分方案如表4 所示。

表4 聚类划分方案Table 4 Clustering scheme

3 种聚类划分方案得到的细、微观单胞聚类分布情况如图5 和图6 所示。相同颜色部分的单元表示具有类似的力学行为，被划分到一个类中。

图5 细观模型聚类分布Fig. 5 Cluster distribution of mesoscale model

图6 微观模型聚类分布Fig. 6 Cluster distribution of microscale model

将3 种聚类划分方案用于多尺度分析中，对比3 种聚类划分方案计算所得材料强度极限，如表5 所示。采用聚类划分方案1，仿真计算强度极限与试验值误差最小，为0.6%；采用聚类划分方案2、方案3，误差分别为0.7%与1.16%，误差略大于方案1 的结果，但仍高于文献[6]的强度极限计算精度。强度极限计算结果表明：随着所选取的聚类数目增多，仿真计算得到的强度极限偏大。这是因为，当聚类数目选取越多时，每个类内所包含的单元会相应减少，一旦损伤发生，发生损伤的单元更少，损伤累积速度更慢，材料刚度的退化也更慢。从而，当外部应变荷载相同时，越多聚类的划分会导致材料计算所得应力较大，当材料发生破坏时，计算所得强度极限也会偏大。

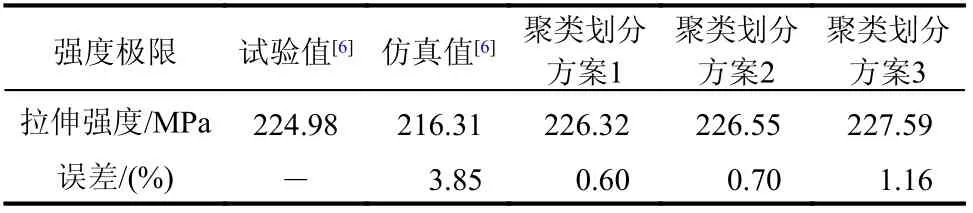
表5 强度极限对比Table 5 Comparison of strength limit

3 种聚类划分方案计算得到的单轴拉伸应力-应变曲线如图7 所示。计算结果表明：当采用更多聚类数目时，应力-应变曲线仅在损伤发生后有细微差别，但整体上是一致的，证明3 种聚类数目的选取方式均是正确的。

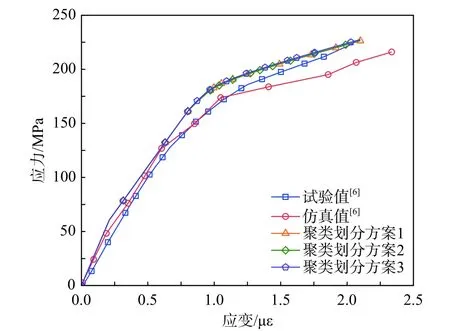
图7 单轴拉伸应力-应变曲线Fig. 7 Stress-strain curves under uniaxial tension

值得注意的是，当聚类数目偏少时，在低阶尺度上无法详细揭示材料的损伤失效过程。因此，采用本方法进行分析时，需要合理选取聚类数目，从而在保证计算效率的同时可以详细模拟低阶尺度上的损伤失效过程。

7 微观界面的影响

为了进一步揭示微观界面对材料强度计算结果的影响，本节开展了不考虑微观界面的2D 编织SiC/SiC 复合材料多尺度分析。保持纤维体积率不变，即将原微观单胞模型界面组分改为基体组分，选取聚类划分数目最多的聚类划分方案3，以相同的聚类数目划分微观纤维、基体，细观纤维束、纯基体，得到的细、微观聚类分布如图8～图9所示。

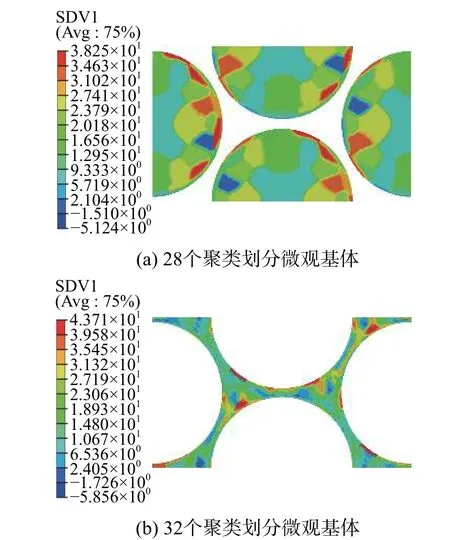
图8 不考虑微观界面情况下的微观模型聚类分布Fig. 8 Cluster distribution of microscale model without considering microscale interfaces

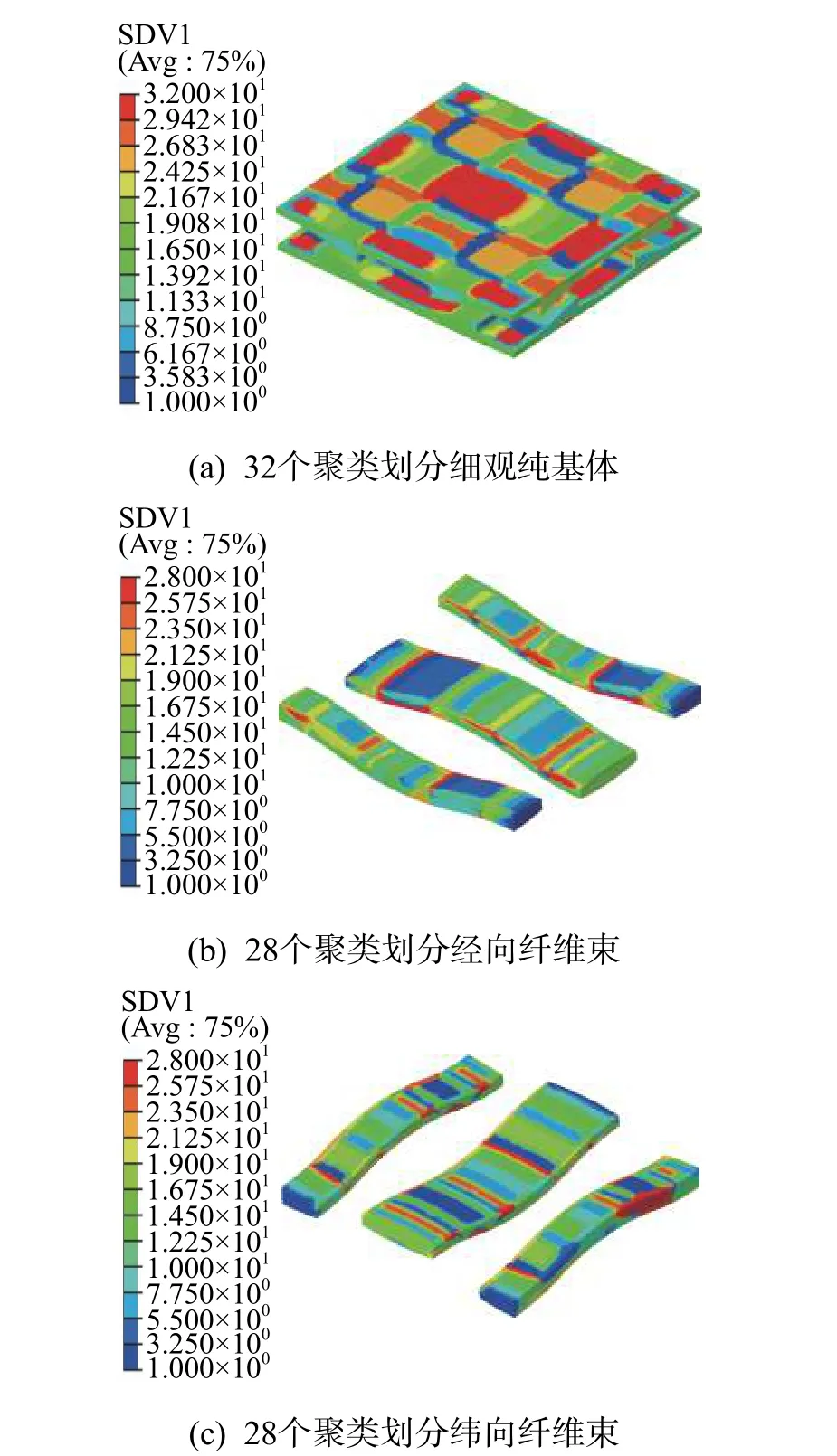
图9 不考虑微观界面情况下的细观模型聚类分布Fig. 9 Cluster distribution of mesoscale model without considering microscale interfaces

将不考虑微观界面情况下计算得到的单轴拉伸应力-应变曲线与考虑微观界面情况下的结果进行对比，如图10 所示。

图10 的对比结果表明，当不考虑微观界面时，仿真得到的单轴拉伸应力-应变曲线与试验结果相差很大，同时材料强度极限计算结果也远高于试验值。这是因为，当不考虑微观界面时，相当于强化了纤维与基体之间的粘结，从而也强化了材料的性能，最终导致了材料整体表现出的抗拉能力远大于其实际抗拉能力。

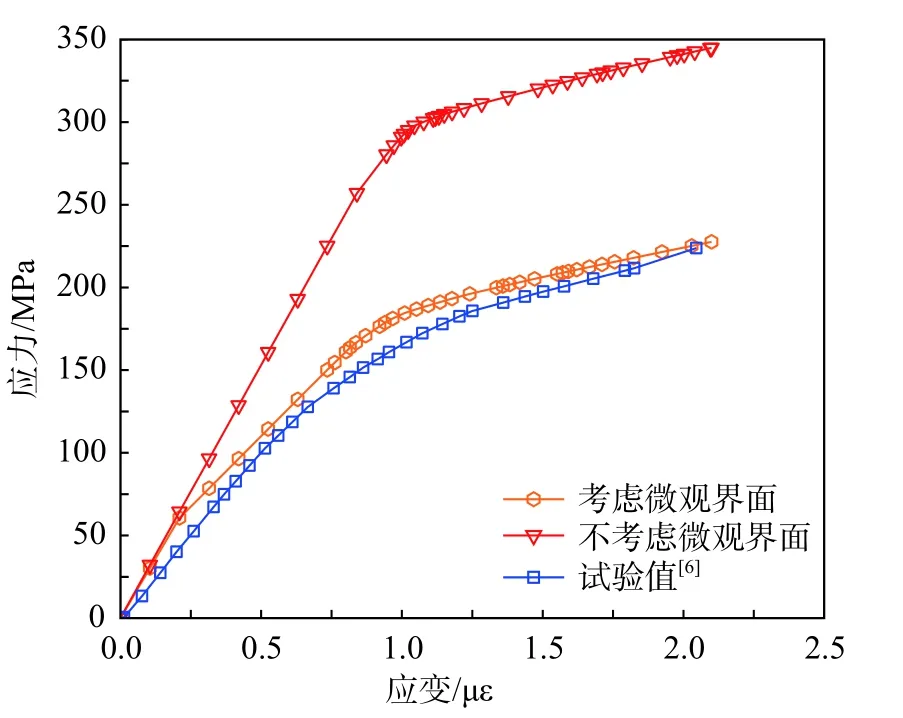
图10 微观界面考虑与否单轴拉伸应力-应变曲线对比Fig. 10 Comparison of stress-strain curves under uniaxial tension with and without microscale interfaces

除了微观界面考虑与否会对仿真计算结果产生影响外，式(10)的微观界面等效损伤变量计算方法也会产生影响。同样选取聚类划分方案3，本节采用式(20)的损伤均匀化方法计算微观界面等效损伤变量并进行多尺度分析。将单轴拉伸应力-应变曲线与第6 节的结果进行对比，如图11所示。

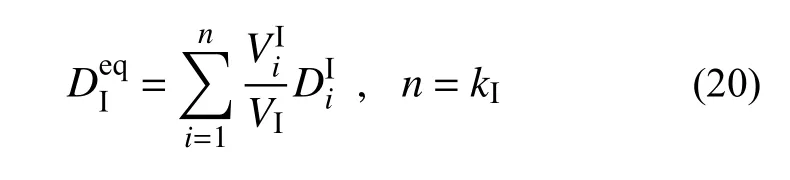
图11 的对比结果表明，若采用损伤均匀化方法计算微观界面等效损伤变量，仿真得到的单轴拉伸应力-应变曲线与试验结果也相差很大，材料强度极限计算结果也高于试验值。这是因为，若采用损伤均匀化方法计算微观界面等效损伤变量，相当于增强了损伤后的微观界面的力学性能，从而也导致了材料整体表现出的抗拉能力大于其实际抗拉能力。

图11 采用不同微观界面等效损伤变量计算方法单轴拉伸应力-应变曲线对比Fig. 11 Comparison of stress-strain curves under uniaxial tension using different calculation methods of microscale interface equivalent damage variables

8 损伤失效过程

如图7 所示，本文仿真计算应力-应变曲线与试验结果对比，当应变荷载相同时，仿真计算应力大于试验应力，且在损伤开始阶段，仿真计算应力与试验应力的误差最大。造成这种情况的原因是材料内部实际存在诸如孔隙等缺陷(见图12)，而仿真模型是未考虑缺陷的理想模型。当未发生损伤时，理想模型由于未考虑缺陷影响，计算刚度大于材料实际刚度，造成了应力-应变曲线线性段仿真计算结果斜率偏大；当损伤开始时，材料在缺陷位置处出现应力集中，相比于仿真结果，材料实际损伤累积更快，损伤程度更严重，造成了仿真计算应力在损伤开始阶段与试验结果误差较大；当损伤持续累积，损伤区域扩展，材料越来越多存在缺陷的部位发生损伤，而仿真模型对应区域也发生损伤，缺陷的影响逐渐减小，仿真计算应力与试验结果趋于一致；当材料接近破坏时，仿真计算应力与试验结果基本相同。

图12 复合材料细、微观缺陷[6]Fig. 12 Mesoscale and microscale defects of composites[6]

选取的聚类数目越多，在低阶尺度上所揭示的损伤扩展过程包含的信息越多。因此，采用聚类划分数目最多的聚类划分方案3 算例，选取宏观模型中间位置处的单元，该位置处由于尺寸没有突变，单元受力均匀，可以将单元对应的细观尺度损伤扩展过程用于与文献[6]的细观尺度分析结果进行对比。如图13 所示，将该单元对应的细观单胞模型每个纯基体聚类损伤程度反映在缩聚的细观单胞模型上，并与文献[6]中细观单胞模型纯基体损伤扩展情况进行对比。结果表明：本文得到的细观纯基体损伤扩展过程与文献[6]中的结果一致。证明本文算例模拟的损伤失效过程正确。

同样采用图13 所选取的宏观单元，将其对应的细观纬向纤维束的微观界面等效损伤变量分布反映在缩聚的细观单胞模型上，如图14 所示。结果表明：在经、纬向纤维束交界位置处，处于纬向纤维束边缘的部分首先出现微观界面的损伤失效，而后损伤区域扩展至纬向纤维束中间的部分，最终纬向纤维束整体出现微观界面损伤失效。

图13 细观纯基体损伤扩展对比Fig. 13 Comparison of damage evolution of mesoscale matrix

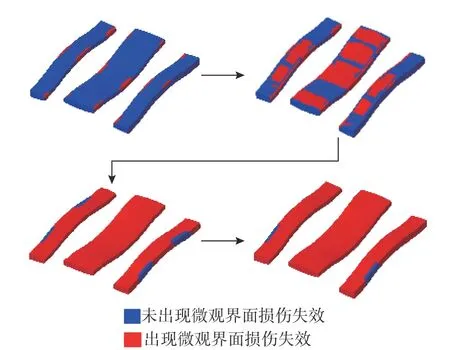
图14 纬向纤维束微观界面等效损伤变量分布Fig. 14 Distribution of equivalent damage variables of microscale interfaces at fill tow

选取纬向纤维束最先出现界面损伤失效的聚类，将其微观界面损伤程度反映在缩聚的微观单胞模型上，如图15 所示。若微观界面某聚类发生损伤，则认为该聚类所包含区域出现界面脱粘破坏，从图15 中可以详细地观察到微观尺度上界面脱粘破坏的过程。

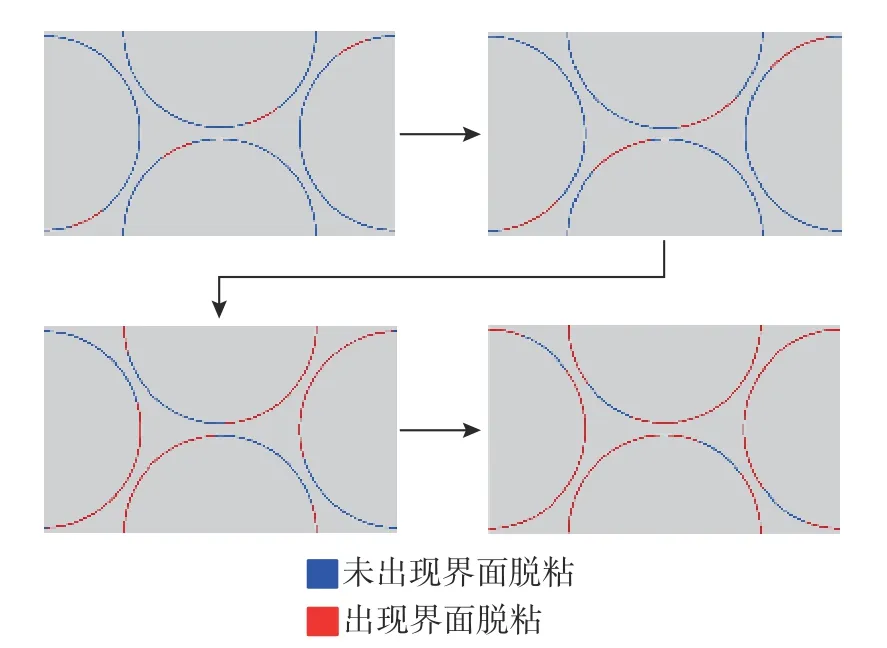
图15 纬向纤维束最先出现界面损伤的聚类对应的微观界面脱粘过程Fig. 15 Microscale interface debonding process of fill tow’s culster where interface damage inititated

相较于文献[6]，本文的多尺度分析结果除了可以模拟低阶尺度上的材料损伤情况外，还可以在宏观尺度上揭示材料力学性能退化、损伤扩展、应力分布等过程。同样采用聚类划分方案3 的算例进行宏观尺度分析结果的展示。

由于纬向纤维束编织方向与材料拉伸方向一致，同时，陶瓷基复合材料拉伸破坏时，沿拉伸方向纤维成簇拔出又是最常见且最主要的失效破坏模式[36-37]。因此，对于本文的多尺度分析结果而言，若宏观模型某单元对应的细观纬向纤维束所有聚类都出现微观界面损伤失效，则近似地认为该宏观单元所处位置可能在拉伸破坏时出现沿拉伸方向纤维成簇拔出。宏观模型可能出现沿拉伸方向纤维成簇拔出的区域分布如图16 所示。图16所示变量的数值达到0.99 的区域表示该区域可能出现沿拉伸方向纤维成簇拔出，其余区域则不会出现沿拉伸方向纤维成簇拔出。结果表明：可能出现沿拉伸方向纤维成簇拔出的区域首先在边缘出现，而后扩展到宏观模型中间部分，最终，在应变荷载达到极限应变荷载时，宏观模型大部分区域均有可能出现沿拉伸方向纤维成簇拔出。

图16 可能出现沿拉伸方向纤维成簇拔出的区域分布Fig. 16 Distribution of zones where tensile-direction fiber bundle may be pulled out

宏观尺度上其他如力学性能退化过程、应力分布情况等也可以通过本文的分析获得。图17 展示宏观尺度上Von Mise 应力分布情况，图18 展示了材料沿拉伸方向弹性模量退化过程。

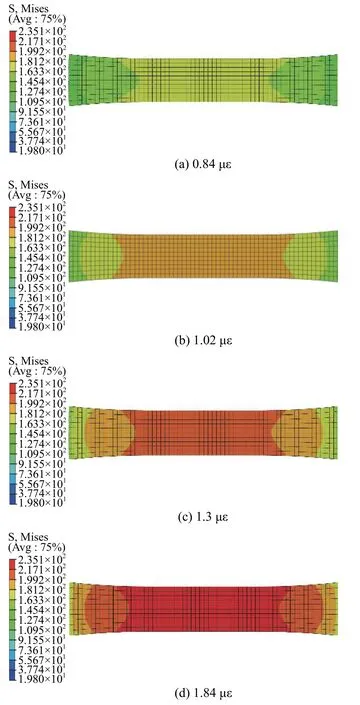
图17 宏观尺度上Von Mise 应力分布情况Fig. 17 Von Mise stress distribution at macroscale

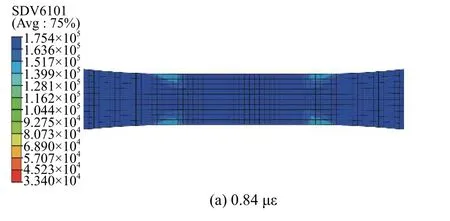
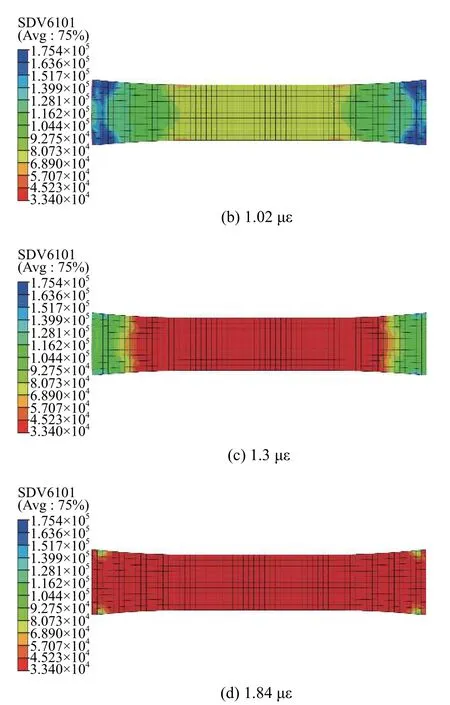
图18 宏观尺度材料沿拉伸方向弹性模量退化过程Fig. 18 Degradation process of elastic modulus along tensile direction at macroscale

9 结论

本文将微观界面组分纳入宏-细-微三个尺度的多尺度渐进损伤失效分析中。采用缩聚的放大因子进行多尺度信息传递，结合相应失效准则及损伤扩展模型对发生损伤的组分进行弹性参数的退化，并结合混合率公式与编织复合材料等效参数计算方法计算宏观模型退化后的弹性参数。进而，针对2D 编织SiC/SiC 复合材料开展了渐进损伤失效分析。结论如下：

(1) 对比3 种不同聚类数目划分方案的计算结果，仿真所得强度极限分别为226.32 MPa、226.55 MPa、227.59 MPa，文献[6]通过试验测得强度极限为224.98 MPa，仿真结果与试验结果一致性均较好，证明了本文所采用聚类数目的正确性。

(2) 微观界面组分在宏-细-微三个尺度的多尺度分析中不可忽略，若不考虑微观界面会导致材料强化，抗拉能力大幅加强。

(3) 微观界面需要按照损伤程度最大的聚类计算等效损伤变量，若采用损伤均匀化方法进行计算，同样会导致材料强化，抗拉能力加强。

(4) 本文模拟的细观纯基体损伤失效扩展过程正确。同时，本文方法可以从细、微观尺度上近似表征材料的界面脱粘过程，从宏观尺度上近似表征沿拉伸方向纤维成簇拔出失效行为。

(5) 本文方法可以从宏观尺度模拟材料的损伤扩展及失效退化过程。