巴哈赛车转向梯形联合优化设计*
李永佶,崔康柬,田顺,杨炜
(长安大学 汽车学院,陕西 西安 710064)
巴哈赛车比赛赛道的路况十分复杂且恶劣,要求赛车的转向系统在满足规则与Ackermann转向关系的前提下能保证良好的操纵稳定性与较强的过弯能力,这就需要巴哈赛车的转向梯形在必要的约束条件下尽可能满足理论Ackermann转向梯形。大部分转向梯形优化设计中为方便计算将转向梯形假设为平面梯形,但由于汽车主销有内倾角与后倾角,实际的转向梯形是一个空间梯形。该文结合长安大学巴哈猎辰车队2021赛季猎辰Ⅴ号赛车转向系统转向梯形设计,根据实际巴哈赛车的主销特性建立数学几何模型,利用MATLAB编写遗传算法优化转向梯形参数来与理论Ackermann转向关系进行拟合,再运用ADAMS虚拟样机进行前悬架模拟跳动优化转向梯形的实际点坐标,保证前悬架跳动过程中轮胎定位参数处于合理变化范围,从而实现转向梯形的联合优化。
1 转向梯形模型建立
1.1 理想Ackermann转向原理
在汽车转向行驶过程中,为避免产生路面对汽车行驶的附加阻力并减小轮胎的过度磨损,要求转向系统能保证汽车所有车轮作纯滚动。要满足该条件,所有车轮的轴线都需相交于一点,转向中心O位于后轴延长线上(见图1)。由几何关系可得出转向轮角度的理想关系式:
(1)
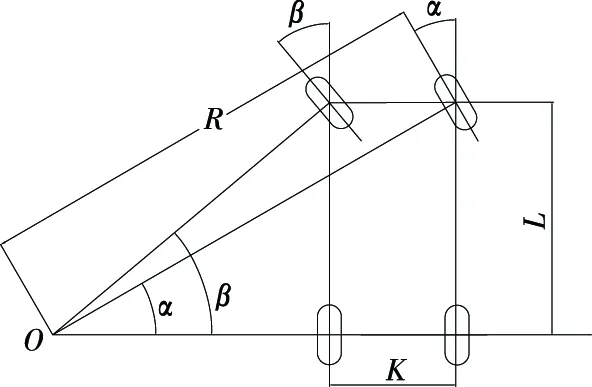
α为理论外轮转角;β为理论内轮转角;K为两侧主销轴线与地面相交点的距离;L为轴距
1.2 实际转向转角关系
理想的Ackermann转向关系实现的前提是把轮胎简化为刚体,而现实中轮胎并非刚体,且有着不可忽略的弹性形变。在行驶过程中,汽车受到路面的侧向倾斜、侧向风或曲线行驶时的离心力等侧向力的作用,因为轮胎的弹性形变,地面对车轮产生侧偏力,使轮胎产生侧偏现象。由于轮胎侧偏,汽车在转向行驶时转向中心O点从后轴延长线上移动至O′点(见图2)。
1.3 优化目标转向关系
对于低速转弯行驶的车辆,采用理想Acker-mann转角关系也就是100%Ackermann系数是合理的。但对于巴哈赛车,为保证赛车在行驶时具有高速过弯能力,通常转弯半径较小,需修正实际的内外轮转角,进而确定转向梯形的Ackermann系数k。公式如下:
(2)
式中:β0为转向过程中实际内轮转角;α0为实际外轮转角。
采用较低的Ackermann系数可减小转弯半径但会产生较大侧偏角,从而对轮胎产生更大的磨损。基于对巴哈比赛赛道路面、巴哈赛车所用轮胎、巴哈赛车实际行驶工况等因素的综合考虑,选用35%的Ackermann系数。
1.4 基本参数的确定
基于赛车的总布置参数及图3所示赛车主销参数进行转向梯形优化的基本参数设置。
实际前轮距rfgg可用下式表示:
rfgg=fgg-2pinoff
(3)
式中:fgg为前轮距;pinoff为主销偏置距。
实际轴距L可表示为:
L=wb-pinbdrag
(4)
式中:wb为轴距;pinbdrag为主销后倾拖距。
两侧主销轴线与地面相交点的距离即转向梯形底边长度K为:
K=rfgg-2htanpinins
(5)
式中:h为转向节臂与主销连接点的高度;pinins为主销内倾角。
由转向几何关系可推出最大外轮转角O:
(6)
式中:R为转弯半径。
由Ackermann转向原理,最大内轮转角i为:
(7)
平均最大转角ave为:
(8)
1.5 转向梯形布置参数的确定
根据车架离地间隙、车架管径和转向机半径等可得出转向机轴线预设高度。为防止转向系统与车架和车身发生干涉,齿条断开点长度应略大于车身宽度。
2 转向梯形拟合优化
2.1 遗传算法
遗传算法是模仿自然界的生物遗传进化机制和自然选择而发展起来的随机全局搜索和优化方法,它模拟的是自然界中生物通过进化与遗传不断朝着适应大自然生存环境方向的进化过程。如图4所示,该算法通过编码将要求解的问题转换为遗传空间的染色体或个体,产生初始种群后,利用适应度函数对种群的适应度进行评估,通过剔除适应度较差的种群,经过交叉、变异运算获得新的种群,找到相似度最高的种群,确定最优解。
2.2 转向梯形遗传算法优化流程设计
利用遗传算法进行转向梯形优化的流程(见图5)如下:
(1)通过对转向梯形的建模与计算确定转向梯形的优化目标与优化对象。
(2)结合赛车赛道行驶状况确定目标函数。
(3)分析实际转向几何在整车上的布置情况与梯形几何的传动关系确定约束条件。
(4)根据转向梯形几何学关系与经验公式确定优化对象的参数取值范围。
(5)使用遗传算法进行优化设计,找到拟合度最高的最优解。
2.3 确定优化对象
图6为前置断开式转向梯形。根据已有分析,转向梯形参数中需优化的对象有转向节臂长度l1、梯形底角φ、梯形高度H。
设F为理论内轮转角。因为巴哈赛车采用35%Ackermann系数,为使巴哈赛车的实际转向转角关系与采用35%Ackermann系数时的理论Ackermann转向转角关系高度拟合,即尽可能使E与F接近,建立转向梯形优化目标函数,在外轮转角j从0°~最大转角O范围内进行转向过程分析。35%Ackermann系数时的理论内轮转角F为:
(9)
由图6所示几何关系可得:
B=
(10)
(11)
(12)
D=
(13)
E=C+D-φ
(14)
2.4 确定目标函数
考虑到巴哈赛车在赛道行驶时多数工况下外轮转角j小于20°,且10°以内的小转角使用更频繁,j大于20°的情况很少,引入式(15)所示加权因子W(j),使目标优化值最小,从而确定目标函数minf。
(15)
(16)
式中:jmax为外轮最大转角。
2.5 建立约束条件
根据图6所示转向梯形几何传动关系,为保证连杆传动良好,应满足横拉杆与节臂传动角δ≥30°,横拉杆与齿条间夹角ξ≤10°。由图6可知:
(17)
同时有:
(18)
(19)
(20)
2.6 取值范围的确定
根据半经验公式得转向梯形理想底角为:
(21)
对于断开式后置转向机构,合适的梯形底角φ应在φ0附近,将其范围扩大30°,则φ取值范围为[φ0-30°,φ0]。
为防止球铰与摩擦盘发生干涉,取二者间距为Boy,需满足:
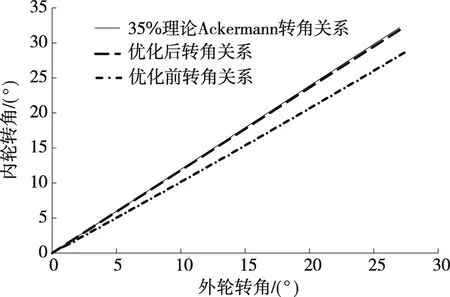
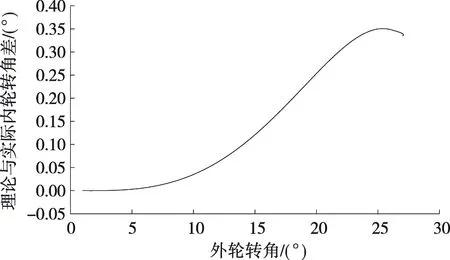
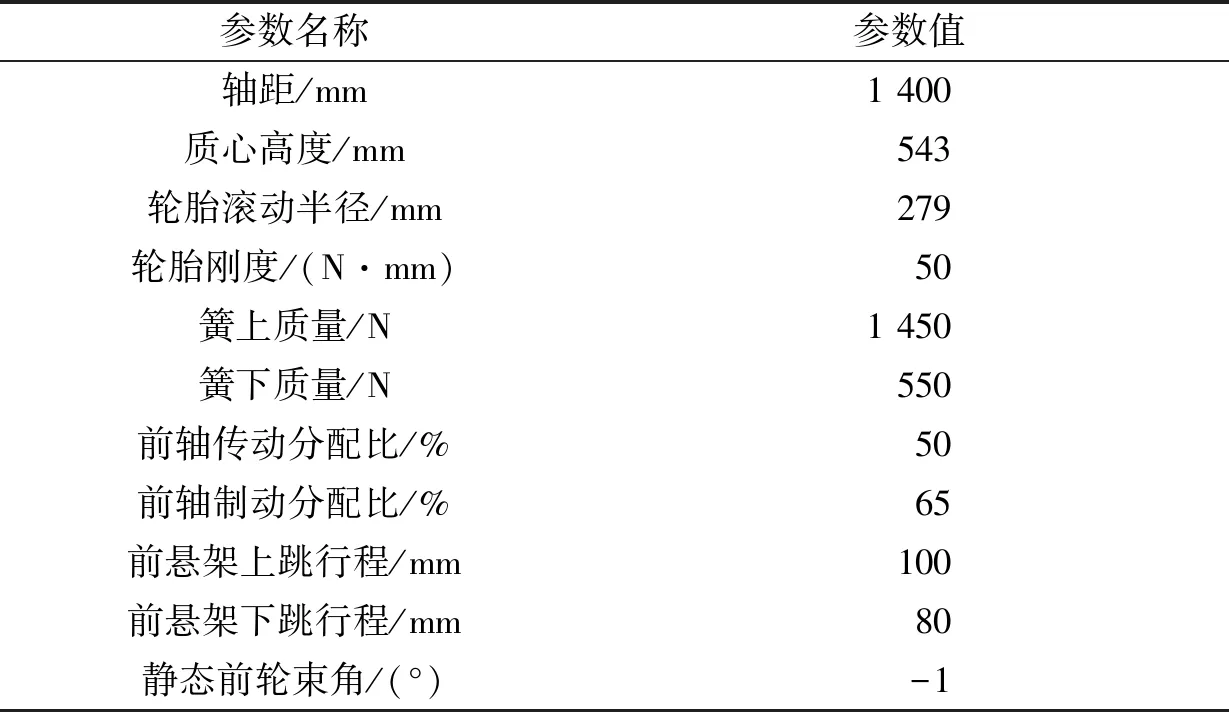
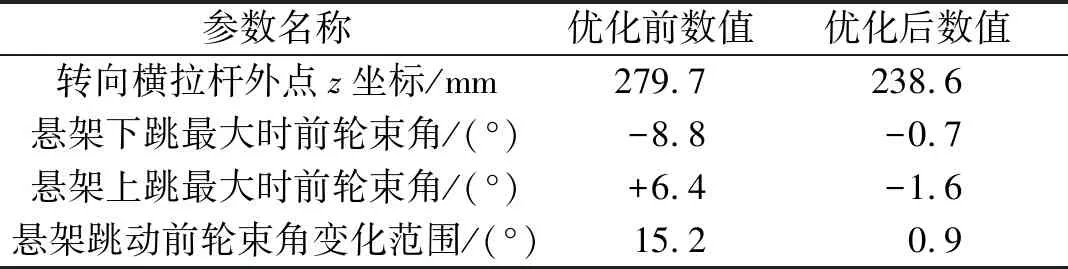
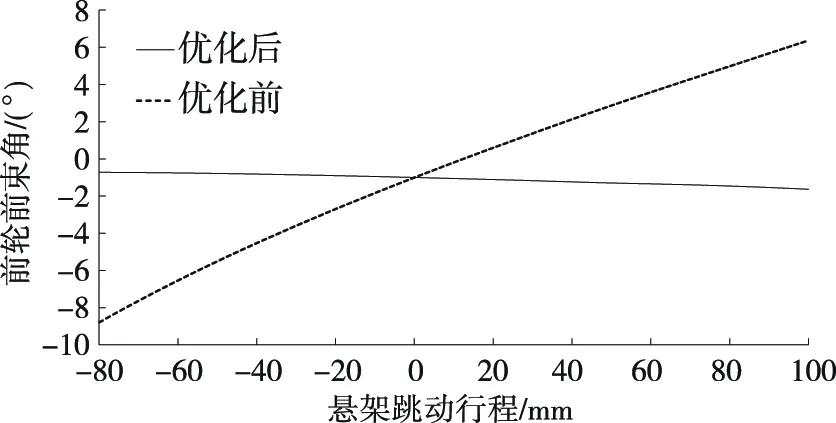
l1×|cosφ(min)| (22) 为防止转向过于沉重,转向节臂长度不能过短,一般令l1>40 mm。 梯形高度H对传动角的影响较大,同时影响转向系的性能。由图6可得: (23) 带入数值计算取整,可得到H的最大值与最小值,从而确定H的取值范围。 取优化对象的初值为: (24) 以前文计算的转向梯形基本参数、目标函数、约束条件函数及转向梯形优化初值为基础,利用MATLAB遗传算法对巴哈赛车实际转向关系与理论Ackermann转向关系进行拟合优化,优化结果见表1。 表1 MATLAB GA遗传算法优化结果 图7为带入整车数据所得巴哈赛车转向梯形理论值及优化前后Ackermann转角关系对比。由图7可知:优化后转角关系曲线与35%理论Acker-mann转角关系曲线的拟合度在外轮转角为0°~10°时最佳,在10°~20°时次之,在20°~jmax时有微弱偏差(1.2%以内)。各段偏差情况与所取加权因子W(j)对应。根据表1,优化后目标函数minf值为0.27,总体上优化后曲线与理论曲线偏差很小,达到了预期优化目标。 图7 转向梯形Ackermann转角关系对比 巴哈赛车的理论内轮转角与实际内轮转角的差值随外轮转角的变化见图8。由图8可知:外轮转角为 0°~jmax时,理论内轮转角与实际内轮转角的最大差值仅为 0.35°,精度较高。 图8 理论与实际内轮转角差 为进一步优化转向梯形结构,对转向轮定位参数影响最大的转向梯形点坐标进行优化。利用表1中数据,结合转向梯形几何关系推导转向梯形各点坐标,与前悬架硬点坐标结合,即可在ADAMS中建立前悬架与转向系统模型。 由ADAMS insight模块分析可知转向梯形的转向横拉杆外点z坐标(tierod_outer,z)对前悬架上下跳动时前轮束角变化的影响最大,为保证车辆在前悬架跳动时束角变化在合理范围内,建立包含前悬架与转向系统的ADAMS/Car模型(见图9)。 图9 前悬架与转向系统的ADAMS模型 将整车参数、轮胎参数、减振器参数等ADAMS分析所需参数数据(见表2)导入ADAMS/Car模型中。设置转向横拉杆外点z坐标为设计变量,根据表2中数据进行前悬架平行轮跳分析,利用ADAMS优化转向横拉杆外点z坐标数值使前轮束角在悬架跳动过程中的变化范围最小。 表2 ADAMS分析主要设置参数 ADAMS/Car优化结果见表3。由表3可知:优化前悬架下跳最大时前束角为-8.8°,上跳最大时前束角为+6.4°,前轮束角变化范围为15.2°,变化范围过大,会使转向操纵不稳,对赛车操纵稳定性的影响很大;优化转向横拉杆外点z坐标后,前悬架下跳最大时前束角为-0.7°,上跳最大时前束角为-1.6°,前轮束角变化范围为0.9°,相较于优化前大大减小,处于合理范围。前束角的变化见图10。 表3 ADAMS/Car优化结果 图10 优化前后前轮前束角变化范围对比 与MATLAB优化后转向梯形各点坐标相结合,完成了转向梯形的联合优化设计,优化确定的转向横拉杆外点z坐标为238.6。 该文提出一种巴哈赛车断开式转向梯形联合优化设计方案,通过分析实际巴哈赛车的主销参数与转向几何关系建立转向梯形几何模型,并确立目标函数与约束函数。按照理论Ackermann转向转角关系,使用MATLAB遗传算法对转向梯形参数进行优化,使实际转向梯形的转角关系与理论Acker-mann转角关系相拟合。使用ADAMS虚拟样机仿真模拟前悬架跳动来优化转向梯形坐标,验证前轮前束角变化范围处于合理范围,转向梯形的优化设计合理。3 优化结果分析
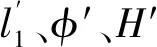

4 ADAMS虚拟样机优化
4.1 建立前悬架与转向的ADAMS模型
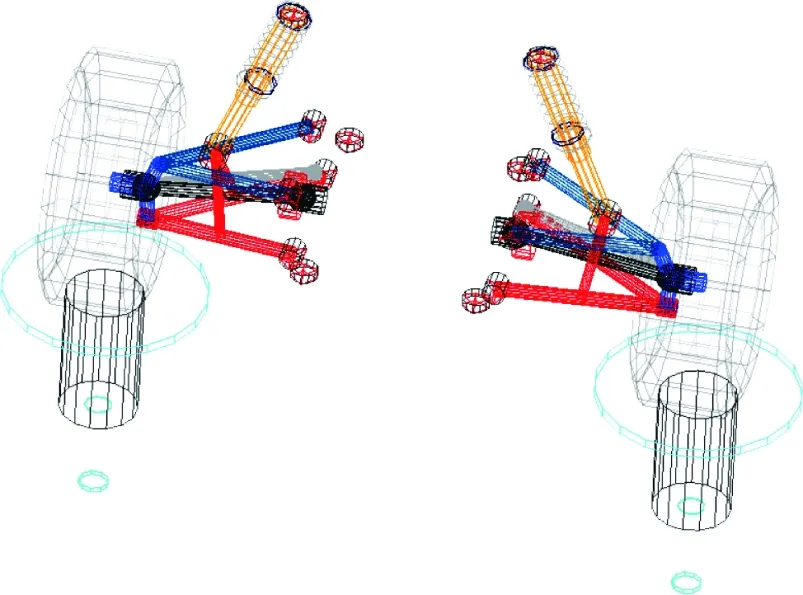
4.2 ADAMS优化结果分析
5 结语

