基于混合算法与大型水箱装配的车间布局*

黄 毅，邓齐林，冯 健，韩志会，马俊燕,b

(广西大学a.机械工程学院；b.广西制造系统与先进制造重点实验室，南宁 530004)

0 引言

设施布局问题(facility layout problem，FLP)就是在一个工厂区域内，在一定的约束条件下，根据某些标准或者目标来确定最有效的布局[1]。合理的设施布局可以加快物料的处理速度，减少中间产品和成品的积压，降低企业运营成本，提高生产效率。大型产品车间布局需要根据产品结构、装配工艺特征以及物流约束，建立数学模型。何坤等[2]考虑了物流和布局面积的约束，提出大型零件布局的解决方法。陈春鹏等[3]通过分析飞机结构件的生产特点，提出多层次的式布局方案，解决了生产车间的布局问题。

张青雷等[4]在考虑大型船舶动力部件的工艺基础上，建立数学模型解决了船用曲轴车间布局问题。对小规模的设备布局，人们可以使用精确方法来模型进行求解，例如动态规划法、分支界定法等。当车间设备大于一定数量的时候，精确解法很难得到最优的解，智能算法为常用的解决方法。王亚良等[5]使用改进的遗传算法改善了制造车间的布局状况。TAYAL等[6]结合大数据分析和混合元启发式算法的方法来求解设施布局问题。周尔民等[7]使用混合算法对车间布局进行求解，得到了较好的结果。为充分考虑物流和非物流因素对车间布局的影响，系统布置设计(systematic layout planning,SLP)被广泛应用于车间布局当中[8]。郭源源等[9]使用粒子群算法与SLP方法来求解连续空间布局问题。侯智等[10]通过遗传算法和SLP方法结合的方式，对仓储物流布局进行了优化，显著提高了仓储物流效率。

基于上述的分析，本文根据大型水箱装配具有小批量，搬运难，装配时间长，主要部件固定在一个位置，其他的部件在完成装配之后运送到这个位置进行总装的特点，为提高产品的装配效率，提出一站式固定的装配布局方案并建立车间布局数学模型，使用SLP方法对车间布局坐标进行初始化，利用粒子群-灰狼混合算法(PSO-GWO)对车间布局问题进行求解，最后以车间案例对算法进行了验证。

1 问题描述与数学模型

1.1 问题描述与假设

车间布局的基本要求是将设备进行有效合理地布置，为方便讨论将设备进行二维抽象化，并做如下假设：①车间布局中的各区域采用已知长和宽的矩形形状；②所有的作业单元共在同一平面，且各矩形只能水平或垂直放置与X轴和Y轴分别平行；③所有的作业单元都必须在一定的区域内布置；④布局中不允许各个单元区域之间重叠；⑤各个作业单元都设置了出入区域位置点，作为计算各个区域之间距离的坐标点。车间设备二维坐标示意图如图1所示。

图1 坐标示意图

1.2 车间布局数学模型

建立物流搬运量最小成本F1。

(1)

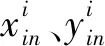
建立车间占地利用率成本函数F2。

(2)

式中，S总为包含整个布局区域的总面积；S用为在整个布局区域里面各个单元区域用掉的总面积；α为面积浪费的惩罚成本值。

建立工艺路线配送成本F3。

(3)

(4)

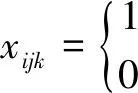
最后，综合三个目标函数，建立总目标函数F总。

F总=min(F1+F2+F3)

(5)

1.3 约束条件

(1)区域不重叠，如下式所示：

(6)

(7)

(8)

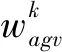
(2)布置区域不超过车间范围，如下所示：

(9)

(10)

式中，W为车间在x轴上的宽度；L为车间在y轴上的宽。

(3)各区域之间保持运输间距，如下所示。

(11)

(12)

(13)

(14)

式中，dxij为局域之间保持的横向距离；dyij为局域之间保持的纵向距离。

2 基于车间布局的混合优化算法

2.1 PSO-GWO模型建立

将灰狼优化算法[11]融入到粒子群算法[9]中，可以平衡粒子群算法在全局搜索和局部搜索中的性能，混合算法如式(15)所示，粒子的飞行速度可根据三只灰狼所寻最优位置值进行动态调整；在式(16)中通过粒子群位置计算公式获得更新位置。

vid(t+1)=w×vid(t)+c1r(X1(t)-xid(t))+
c2r(X2(t)-xid(t))+c3r(X3(t)-xid(t))

(15)

xid(t+1)=xid(t)×vid(t)

(16)

式中，vid表示第i个粒子在第d维空间的速度；xid表示第i个粒子在第d维空间的位置；w表示惯性权重因子；t为迭代的次数；r为[0,1]的均匀随机数；c1、c2、c3为学习因子，并设定φ1=c1+c2+c3，且φ1的值等于粒子群算法中学习因子的和;X1(t)、X2(t)、X3(t)分别代表种群中三匹最优秀狼的当前位置。

2.2 PSO-GWO算法设置

采用文献[12]中介绍的线性微分递减策略来设定惯性系数，其表达式如式(17)所示：

(17)

式中，wmax为最大惯性系数;w为最小惯性系数;tmax为设定的最大迭代次数。

将适应度函数设定为式(5)。

算法流程如下：

步骤1：初始化PSO-GWO算法的参数；

步骤2：根据式(5)计算种群的适应度值，根据种群适应度值，保留最佳的三匹狼，并更新其位置信息；

步骤3：更新灰狼优化算法的内部参数；

步骤4：根据式(15)和式(16)，更新粒子当前最优位置，根据式(17)更新惯性系数；

步骤5：判断是否达到迭代次数，若到达迭代最大值，获得最优方案，否则返回步骤2继续寻优。

3 车间案例验证

3.1 初始车间布局概述

A企业主要从事多种环保产品研发、设计、制造生产和营销的一体化环保科技企业，其生产的环保装备产品市场需求量高，需要进行对生产布局进行科学的规划以提高生产效率，降低生产成本。该企业生产的四节环保水箱长4 m，宽2 m和高2 m，其组成部件主要有底盖、顶盖、端盖、隔板和管道。具体参数如表1所示。

表1 单个环保水箱的部件尺寸和数量 (m)

装配车间长50 m，宽40 m，主要包括其各个部件存储区，组装区以及成品存储区，如图2所示。

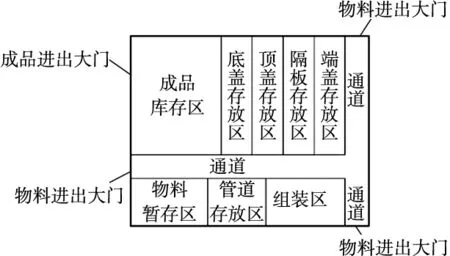
图2 原始车间布局

原生产布局存在诸多问题，①装配部件的存放区和组装区布局情况不合理，增加了部件的搬运距离；②没有设置部件的部装区域，全部零件都搬运到组装区进行组装，生产效率不高。

3.2 一站式布局方案

针对以上提到的问题，提出一站式的布局方案。根据产品的结构特点和生产加工流程，设置11个单元区域，如表2所示，其中，进出口区域比例是对各区域的物流入口和物流出口进行设定，以增加模型的准确性。

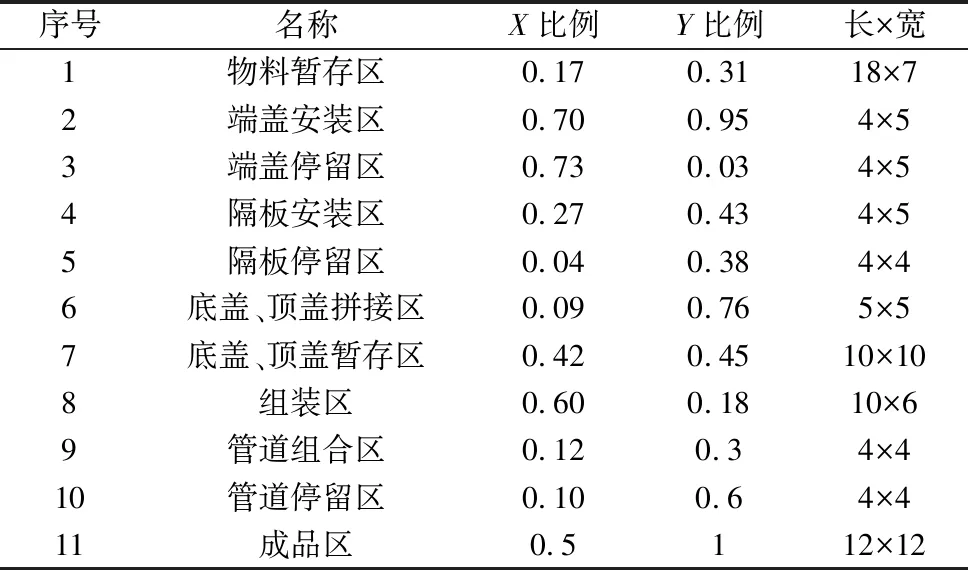
表2 作业单位参数设置 (m)

使用SLP方法获取各区域的初始布局坐标，可以避免随机生成的区域初始坐标给车间布局带来的不确定性，并且充分考虑到物流和非物流因素，使得优化结果更贴合生产实际。SLP方法获得的初始坐标如表3所示，作业单元相关关系如图3所示。

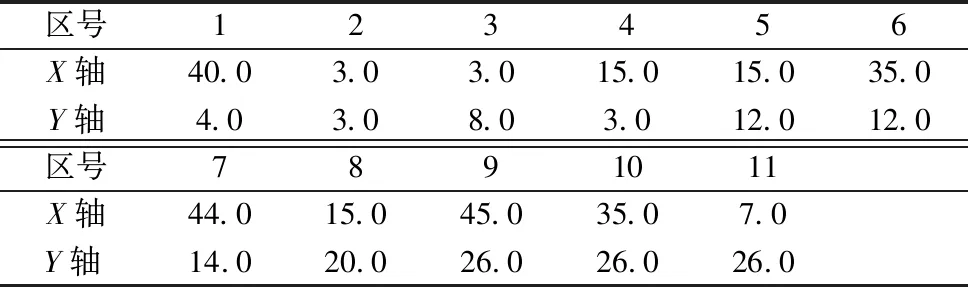
表3 使用SLP方法获取的初始布局坐标 (m)

图3 作业单元位置相关关系图

对表3和图3进行综合分析，设置各部件的工艺路线，分别对端盖、隔板、顶盖、底盖以及管道进行分装，并各自放置在暂存区，之后运送至区域8进行总装，最后运送至区域11存放。工艺路线设置如表4所示。

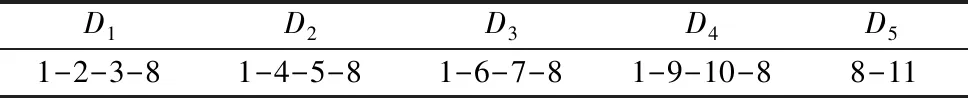
表4 各部件的工艺路线

3.3 基于PSO-GWO算法的车间布局优化

通过PSO-GWO算法对上述的车间数学模型进行求解，区域数量(粒子维度)n为11，种群规模nPop为80，迭代次数t为100，惯性系数w最大值设置为1.2，最小值为0.8，学习因子c1，c2，c3的设定为三个水平。为寻找出比较合适的学习因子，设计了3种有代表性的方案，并从中选择最优的一组，运用到车间布局当中。

在MATLAB上使用PSO-GWO算法对车间布局进行仿真实验，使用SLP方法获得初始坐标，每个方案运行20次，取其中最优的5次的平均值作为评价标准，三种方案的运行结果如表5和表6所示。

表5 三种方案的最优5组优化结果对比

表6 三种方案运行20次的统计结果

3.4 结果分析

PSO-GWO算法对车间布局进行仿真结果的最终的坐标如表7所示，与表3对比发现，每个区域之间的位置和初始坐标相比都有了一定的变化，展示了算法对目标函数的寻优结果。最终的各工作区域间工艺路线距离和适应度如表8所示，各布局装配区域之间的工艺路线也得到了优化，搬运的距离减少45.8%，适应度降低约29%。

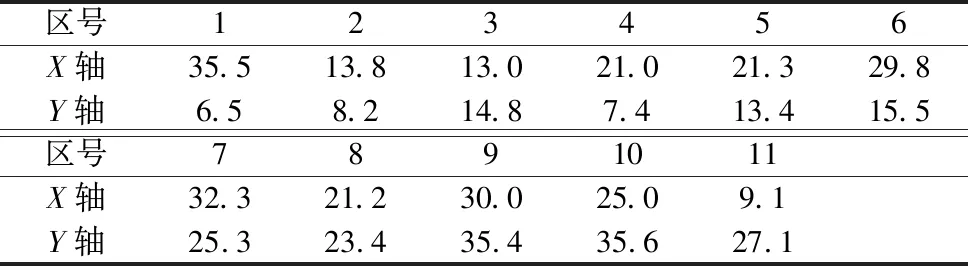
表7 PSO-GWO算法获得的布局坐标 (m)

表8 PSO-GWO算法获得工艺路线距离和适应度

最终的布局方案如图4所示。空心点为物流进入入口，黑点为物流流出出口。对比表2 、表3、表4和图2的初始布置情况，运用SLP方法和智能算法优化之后的车间布局不仅能够满足综合成本最低的需求，还充分考虑了工艺路线的连续性、人员流动的方便性等非物流因素。

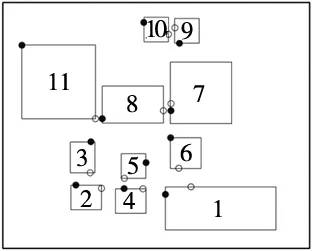
图4 车间布局图

4 结论

(1)在使用了SLP方法的前提下，作业单元获得了初步的布局，对算法的寻优能力提出了挑战。在粒子群算法中引入灰狼优化算法的策略，有益于算法跳出局部最优，寻找到全局最优的方案。

(2)产品装配车间布局需要根据产品实际的工艺特点设置相应的布局方法，本文提出的一站式装配布局方法是针对大型产品装配布局的一次有益的尝试。给出了一个车间的实例，仿真结果表明，本文提出的装配车间优化方法能够有效地解决实际问题，提高企业的生产效率。