绝对重力测量中振动传感器振动补偿性能的分析*

文艺 伍康 王力军

(清华大学精密仪器系，精密测试技术及仪器国家重点实验室，北京 100084)

绝对重力测量的精度主要受振动噪声的限制.振动补偿是一种简单可行的振动噪声处理方法，它通过传感器探测振动噪声来对测量结果进行修正.现阶段对于不同传感器的振动补偿性能缺乏系统的分析与评估，仅停留在应用阶段.本文从理论出发分析了传感器性能对补偿效果的影响，并通过实验评估了不同振动环境下不同传感器的振动补偿性能.实验结果显示，采用低噪声地震计的振动补偿效果主要受带宽和量程的限制，在安静环境下可实现优于百微伽的单次测量标准差，但补偿效果随振动噪声高频成分的增强而降低，在动态环境下地震计则受量程限制而无法工作.采用加速度计的振动补偿效果主要受分辨率的限制，在复杂和动态环境下均可实现毫伽量级的单次测量标准差.本文为振动补偿技术应用于绝对重力测量提供了振动传感器选型的理论和实践依据，有望为振动补偿技术的进一步发展提供技术支撑.

1 引言

地表重力加速度(g，常用值9.8 m/s2)的精密观测结果广泛地应用于地球物理学、计量学、大地测量学等领域[1-3].重力加速度绝对值的测量被称为绝对重力测量，通过绝对重力仪来实现.激光干涉式绝对重力仪是目前应用最广、精度最高的绝对重力测量工具[2-4].它以稳频激光器和铷钟分别作为长度基准和时间基准，通过干涉仪测量真空中物体做自由落体运动的轨迹，再对自由落体轨迹进行二次拟合来得到g值，可实现μGal (1 μGal=10—8m/s2)量级的测量不确定度[5，6].其测量误差主要来自地面振动噪声[7]，综合考虑噪声强度、频率和相位因素的影响，对于复杂振动环境下的振动补偿应用，消除或衰减 0.1—100 Hz 范围的噪声所造成的干扰是实现优于毫伽量级重力测量不确定度的关键[8-13].

隔振和振动补偿是绝对重力测量处理振动噪声的两种主要方法[14，15].其中，振动补偿是通过传感器探测振动噪声来修正测量值，具备强振动环境下开展绝对重力测量的应用潜力，但振动传感器的性能制约着振动补偿效果.目前常用于振动补偿的振动传感器有两类:宽频带地震计和加速度计.宽频带地震计分辨率较高，其带宽约在0.01 Hz—80 Hz，相对于振动补偿应用较窄，对于高频振动存在探测信号失真问题，而且量程较小通常不适用于较强振动噪声及移动平台环境;加速度计测量分辨率比宽频带地震计要低，但带宽可达数百Hz 甚至kHz 量级，量程一般都超过 ± 2 g，可以适应较强振动噪声及移动平台环境.以卡尔加里大学、中国计量院、清华大学、浙江大学和法国巴黎天文台等为代表的研究机构采用地震计实现了实验室环境下的振动补偿，补偿后单次测量标准差达到百微伽量级[15-20].以苏黎世联邦理工学院、法国航空航天实验室、浙江工业大学等为代表的研究机构则应用加速度计进行了野外或移动平台的振动补偿，补偿后单次测量标准差达到毫伽量级[21-24].然而上述振动补偿技术的研究并未系统分析和比较传感器的性能指标对振动补偿效果的影响.

本文通过理论分析和对比实验研究了振动传感器主要性能指标在不同振动环境下对绝对重力仪振动补偿精度的影响，提供了振动传感器选型的理论依据和实验验证，有望为发展振动补偿技术、提高补偿精度提供技术支撑.

2 振动补偿

2.1 原 理

目前典型的激光干涉式绝对重力仪是基于马赫-曾德尔干涉测量原理来测量下落棱镜的自由落体运动轨迹，如图1(a)所示.激光器准直后发出的光束经分光镜分为两路，透射光为参考光，反射光为测量光.测量光经下落棱镜和参考棱镜反射后与参考光重合并发生干涉，干涉条纹的数量反映自由落体过程中测量光的光程变化.因此，干涉测量得到的自由落体轨迹Sm实际上是下落棱镜相对参考棱镜的运动轨迹.假设下落棱镜做理想自由落体运动S，下落测量过程中参考棱镜受噪声干扰而产生的运动为N，则理想自由落体运动轨迹S与实际测量轨迹Sm的关系为

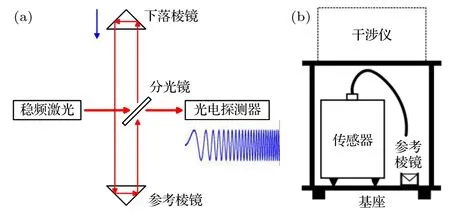
图1 (a)激光干涉测量和(b)振动补偿的原理示意图Fig.1.Schematic diagram of (a) laser interferometry and(b) vibration correction.

由此可见，参考棱镜的运动N给测量轨迹Sm引入了误差.振动补偿的原理就是利用传感器测量参考棱镜的运动N来对干涉测量轨迹Sm进行修正，系统结构如图1(b)所示.由于传感器的敏感结构和参考棱镜是不同的物体，传感器测量所得运动Nm并不等价于参考棱镜的真实运动N，两者之间存在偏差 ΔN.采用传感器探测信号Nm对测量轨迹Sm进行修正，修正后的轨迹Sc为

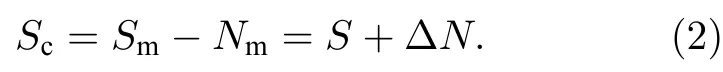
由此可见，传感器探测误差 ΔN也是修正后的轨迹Sc与理想自由落体轨迹S间的误差.因此如何减小探测误差 ΔN，使传感器的探测信号Nm尽可能接近参考棱镜真实运动N是实现高精度振动补偿的关键.

传感器输出Nm和参考棱镜真实运动N的关系如图2 所示，两者之间的传递函数关系G(s)可以表示为

图2 传感器输出与参考棱镜运动的关系Fig.2.Relationship between the output of sensor and the motion of reference retro-reflector.

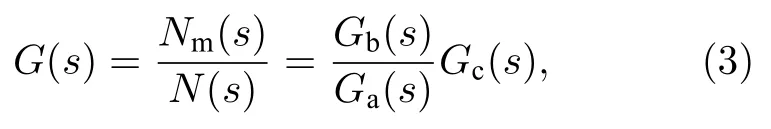
式中Ga为地面振动X0到参考棱镜运动N的传递函数，Gb为地面振动X0到传感器输入的传递函数，Gc为传感器的传递函数.要实现高精度的补偿效果，需要从传感器输出的Nm尽可能准确地还原参考棱镜运动N.由(3)式可知有两个关键因素:一个是振动补偿算法，其作用在于尽可能准确地求解传感器输出和参考棱镜运动间的传递函数G(s);另一个是传感器的性能，其作用在于使传感探测到的信号Nm尽可能得准确，从而可以结合补偿算法还原出参考棱镜的真实运动N.

2.2 算 法

补偿算法的关键在于求解传递函数G(s).目前已有不少关于补偿算法的研究，由于真实传递函数G(s) 的复杂性，现有补偿算法均将G(s)进行了合理的简化[15-17，25].本文采用课题组已有的振动补偿算法[16]，该算法将传递函数G(s)简化为增益延时模型Gs(s)，传感器输出Nm与参考棱镜运动N的关系可表示为

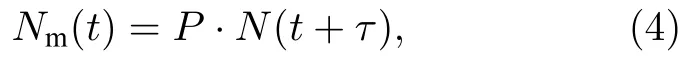
其中，P为增益，τ为延时，两者均为待确定的未知参数.

参数求解过程分为两步:先利用相关分析法求解延时τ，取传感器信号所得位移的拟合残差和干涉测量轨迹的拟合残差相关系数最大处的延时作为延时参数τ;再采用遍历法以单次补偿后的拟合残差标准差最小为优化目标，确定增益P的最优解，最终求解出补偿传递函数Gs(s)[16].

2.3 振动传感器

振动传感器的性能也是影响补偿精度的关键因素之一，其中分辨率、带宽和量程是需要重点关注的性能指标.由于传感器的输出通常包含有效信号和自噪声，若有效信号的强度小于自噪声则会被噪声淹没，导致传感器输出信噪比过低而无法使用.因此要实现目标精度的振动补偿，首先传感器的分辨率(即仪器自噪声)要优于目标精度，如优于5—10 倍及以上.当传感器的分辨率满足目标补偿精度的需求时，其补偿效果仍会受传递函数带宽的影响，这主要是由传感器的真实传递函数与补偿算法所用的简化模型不等价所导致.在传感器传递函数的—3 dB 带宽附近以及带宽外，其幅值随频率的变化为非线性衰减，不满足增益延时模型中增益为常值的特性;其相位随频率的变化也不能近似为线性关系，不满足增益延时模型中延时环节的特性.因此若传递函数的带宽较小，无法保证在目标频带内满足补偿算法所用模型的简化条件，则无法从传感器输出得到真实准确的参考棱镜运动，从而影响补偿精度[13].此外，传感器的量程决定了传感器能工作的测量范围，在振动幅值超出量程的测量环境下，传感器无法进行有效的振动补偿.

综上所述，传感器的分辨率和带宽是保证补偿精度的基础，而量程则主要限制振动传感器所能承受的最大振动环境.此外，长期稳定性等其他特性也会影响传感器输出信号的精度，从而影响补偿效果.

3 实验系统与过程

3.1 实验系统

实验采用基于振动补偿的绝对重力测量系统，主要由真空腔、干涉仪和振动补偿装置组成，如图3(a)所示.采用超低频垂直隔振器的T-3 型高精度绝对重力仪常用于安静环境下的高精度绝对重力测量，其合成不确定度为7 μGal.图3(b)为T-3 型高精度重力仪在西安中心地震台24 小时的重力测量结果，统计不确定度为2.7 μGal.因此测量精度更优的T-3 型高精度重力仪可用于验证传感器的振动补偿效果.

图3 (a)基于振动补偿的T-3 型绝对重力仪示意图;(b) 基于超低频垂直隔振的T-3 型高精度绝对重力仪在西安中心地震台的重力测量结果.Fig.3.(a) Schematic diagram of T-3 type absolute gravimeter using vibration correction;(b) tidal gravity measurement conducted by T-3 type high-precision absolute gravimeter using ultra-low frequency vertical vibration isolator at Xi’an Seismological Station.

振动补偿装置采用地震计和加速度计两种振动传感器，均紧密放置在参考棱镜附近.实验选用的地震计包括英国Guralp 公司生产的 CMG-3ESP型地震计和中国港震公司生产的CS60 型地震计，加速度计是航天科工三院33 所研制的JN06D 型高精度石英挠性加速度计.地震计和加速度计的相关性能指标如表1 所列.传感器输出信号的采集通过NI 公司的24 位数据采集卡PCI-4462 来实现，实验中采用200 kS/s 的采样率同时采集4 个通道的输入信号.

表1 振动传感器性能指标Table 1.Characteristics of vibration sensors.

3.2 实验过程

为进行不同振动环境下不同传感器补偿效果的对比评估，重力仪系统在3 种振动环境下比较地震计和加速度计的补偿性能，如图4 所示.第一种振动环境为中国计量院昌平园区内重力实验室的隔离地基，实验装置如图5(a)所示.昌平计量院的地基稳固性高，整体振动小于0.1 μg (RMS 值，带宽 ＜ 10 Hz)[26]，承办过2017 年国际重力比对，是一个非常安静的振动环境，因此将该地基称为安静地基.第二种振动环境为清华大学焊接馆实验室内的地基，实验装置如图5(b)所示.该实验室地基不是隔离地基，距离地铁13 号线约800 m，距离校内主要道路约10 m，受校内施工、人流车流密集往来等因素的影响，地面振动较昌平地基大且高频成分增加，对于绝对重力测量来说属于嘈杂的振动环境，因此将该地基称为嘈杂地基.第三种振动环境为放置在清华大学焊接馆实验室内的被动万向悬架，重力仪系统固连在万向悬架的内框架中，如图5(c)所示.万向悬架的稳固性远不如地基，除了地面振动噪声外，万向悬架上的仪器自振动也大大增加，该环境下振动噪声接近或超过地震计量程，仅采用加速度计进行振动补偿.

图4 实验采用的不同振动环境类型Fig.4.Different cases of vibration environments for experiments.

振动补偿实验包括两个步骤:第一步是采集数据，在重力测量的同时采集多个传感器的输出信号和干涉条纹采集的触发信号;第二步是数据后处理，将传感器输出信号利用触发信号与下落测量轨迹进行大致的同步标定，再分别采用不同传感器数据进行振动补偿，并比较不同传感器的补偿结果.在不同振动环境下重复上述实验操作，比较同一振动环境下不同传感器补偿性能的优劣以及不同环境下同一传感器补偿性能的变化.

4 实验结果与分析

4.1 实验结果

振动补偿结果如表2 所列，表中计算系统偏差所用的真值g0为FG5(合成不确定度2 μGal)或A10 (合成不确定度10 μGal)在相应测量点的标定值.图6 和图7 中的误差带表示95%置信水平下的扩展不确定度，k为扩展不确定度的包含因子[26].

图6 安静地基上的结果对比 (a)逐点分布;(b)含误差带的均值(k=2)Fig.6.Comparison of results on the quiet ground:(a) Drop-to-drop scatter of g;(b) mean value with expanded uncertainty (k=2).

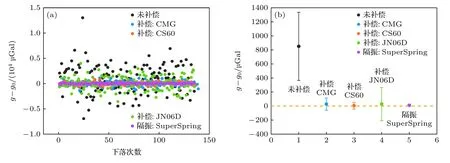
图7 嘈杂地基上的结果对比 (a)逐点分布;(b)含误差带的均值(k=2)Fig.7.Comparison of results on the noisy ground:(a) Drop-to-drop scatter of g;(b) mean value with expanded uncertainty (k=2).

对于安静地基的振动环境，如图6 所示，两款地震计的补偿性能接近，补偿后的单次测量标准差均为70 μGal 左右.采用JN06D 型加速度计补偿后的单次测量标准差则由补偿前的120 μGal 增大至578 μGal.

对于嘈杂地基的振动环境，如图7 所示，采用地震计和加速度计补偿后的系统偏差和单次测量标准差都得到明显改善.采用CS60 型地震计、CMG 型地震计和JN06D 型加速度计补偿后的单次测量标准差分别为289，511 和1374 μGal.然而两种地震计的补偿效果均不如隔振，且相比安静地基环境的补偿效果有所下降，其中带宽更小的CMG型地震计补偿效果下降更明显.

对于万向悬架的振动环境，图8 给出了JN06D型加速度计在下落过程中测得的振动加速度，幅值约为0.1 m/s2，频率约为12 Hz.根据表1所列，这一振动幅值已经接近CMG 型地震计和CS60 型地震计的输入限幅，因此在万向悬架上并未采用地震计进行振动补偿.而JN06D 型加速度计则补偿效果明显，如图9 所示，补偿后系统偏差由—1158 mGal 修正为—285 μGal，单次测量标准差由43 mGal 减小为3.3 mGal.

图8 万向悬架上JN06D 测得单次下落过程中的振动加速度Fig.8.Vibration acceleration measured by JN06D on the gimbal during a single drop.

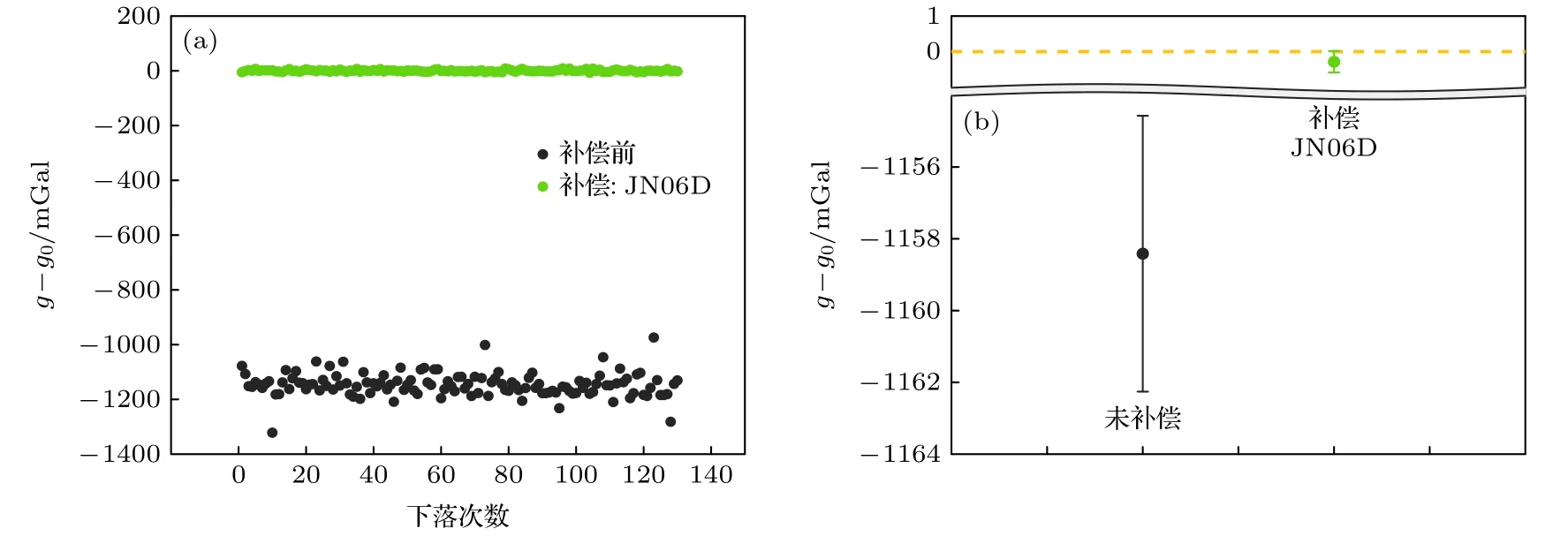
图9 万向悬架上的结果对比 (a)逐点分布;(b)含误差带的均值(k=2)Fig.9.Comparison of results on the gimbal:(a) Drop-to-drop scatter of g;(b) mean value with expanded uncertainty (k=2).

4.2 分析讨论

本节根据单次补偿情况来具体分析同一振动环境下不同传感器的补偿性能以及同一传感器不同振动环境下补偿性能的变化.

在安静地基的振动环境下，补偿前的原始拟合残差幅值约为6 nm，主导频率成分约为20 Hz，如图10(a)所示.这表明安静地基上参考棱镜所受振动噪声的幅值很低，且以20 Hz 左右的低频噪声为主，因此补偿前的单次测量标准差较低.一方面这与安静地基的地脉动噪声更小有关;另一方面也与安静地基对真空腔和参考棱镜的物理隔离作用有关.重力测量过程中仪器产生的反冲振动通过地基传导至参考棱镜处，因此地基越稳固，对反冲振动的衰减越明显，参考棱镜所受振动幅值越小，且以低频为主[11].在安静地基上，两款地震计的分辨率可实现对小振幅低频振动噪声的高精度探测.且主导振动噪声的频率范围均位于两款地震计带宽内的响应平坦区域，有利于增益延时模型实现良好的补偿效果.从图10(a)和图11(a)可以看出，CMG型和CS60 型地震计的探测位移拟合残差和原始拟合残差相关性很高，印证了地震计良好的振动探测性能和模型的有效性，因此补偿后得到的拟合残差低频噪声幅值衰减且更接近于白噪声，测量结果也得到改善.由于两款地震计的带宽均满足对低频主导振动噪声的探测需求，因此两种地震计的补偿效果接近.而JN06D 型加速度计的分辨率只有毫伽量级，对于百微伽量级的振动信号无法实现良好的探测.如图12(a)所示，JN06D 所得探测位移的拟合残差和原始拟合残差相关性差，因此采用不准确的探测信号无法实现补偿效果.

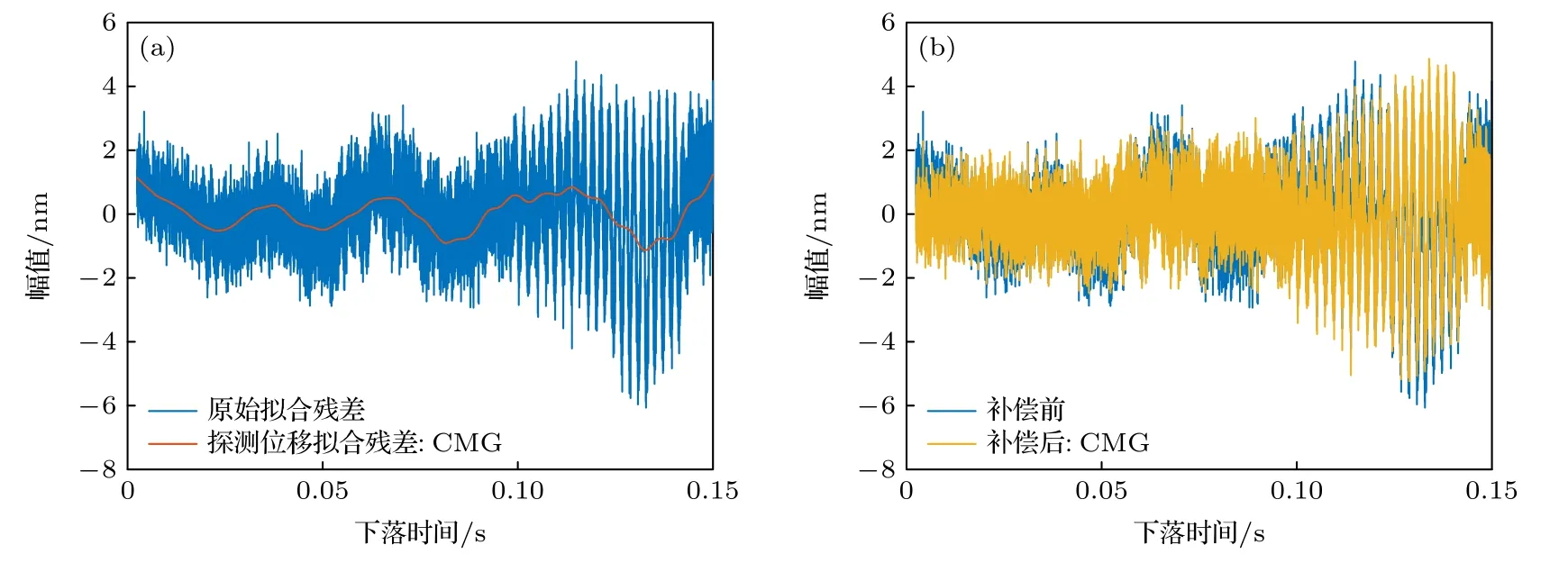
图10 安静地基上CMG 单次补偿的情况 (a)原始拟合残差与探测位移拟合残差对比;(b)补偿前后拟合残差对比Fig.10.Correction for single drop using CMG data on the quiet ground:(a) Residuals of measured trajectory Sm and measured vibration noise Nm;(b) residuals of measured trajectory Sm before and after correction.

图11 安静地基上CS60 单次补偿的情况 (a)原始拟合残差与探测位移拟合残差对比;(b)补偿前后拟合残差对比Fig.11.Correction for single drop using CS60 data on the quiet ground:(a) Residuals of measured trajectory Sm and measured vibration noise Nm;(b) residuals of measured trajectory Sm before and after correction.

图12 安静地基上JN06 D 单次补偿的情况 (a)原始拟合残差与探测位移拟合残差对比;(b)补偿前后拟合残差对比Fig.12.Correction for single drop using JN06 D data on the quiet ground:(a) Residuals of measured trajectory Sm and measured vibration noise Nm;(b) residuals of measured trajectory Sm before and after correction.

在嘈杂地基的振动环境下，地基的稳固性相比安静地基下降，一方面噪声源和噪声强度增加，另一方面地基对反冲振动的衰减作用减小.从图13(a)可以看出，原始拟合残差的幅值约为60 nm，是安静地基环境的10 倍，振动噪声高频成分明显增加且幅值增强，因此补偿前的单次测量标准差相比安静地基环境增加，达到毫伽量级以上.对比图13(a)和图14(a)可知，尽管仍能有效探测振动信号，但两款地震计都受带宽限制出现了不同程度的高频信号失真.其中带宽更大的CS60 型地震计高频失真程度较低，其探测信号相比CMG 型地震计包含更多的高频细节，更接近真实振动，因此补偿后的拟合残差幅值更小，补偿效果也更好.对于JN06D 型加速度计，其毫伽量级的分辨率可以实现该环境下振动噪声的有效探测，高达kHz 的带宽可避免高频信号失真.如图15(a)所示，JN06D 的探测信号拟合残差与原始拟合残差具有一定相关性，其中探测信号高频分量很强，与真实振动接近，但低频分量与真实振动的匹配度不如地震计高，因此加速计的补偿效果不如地震计，这主要是受分辨率的限制.

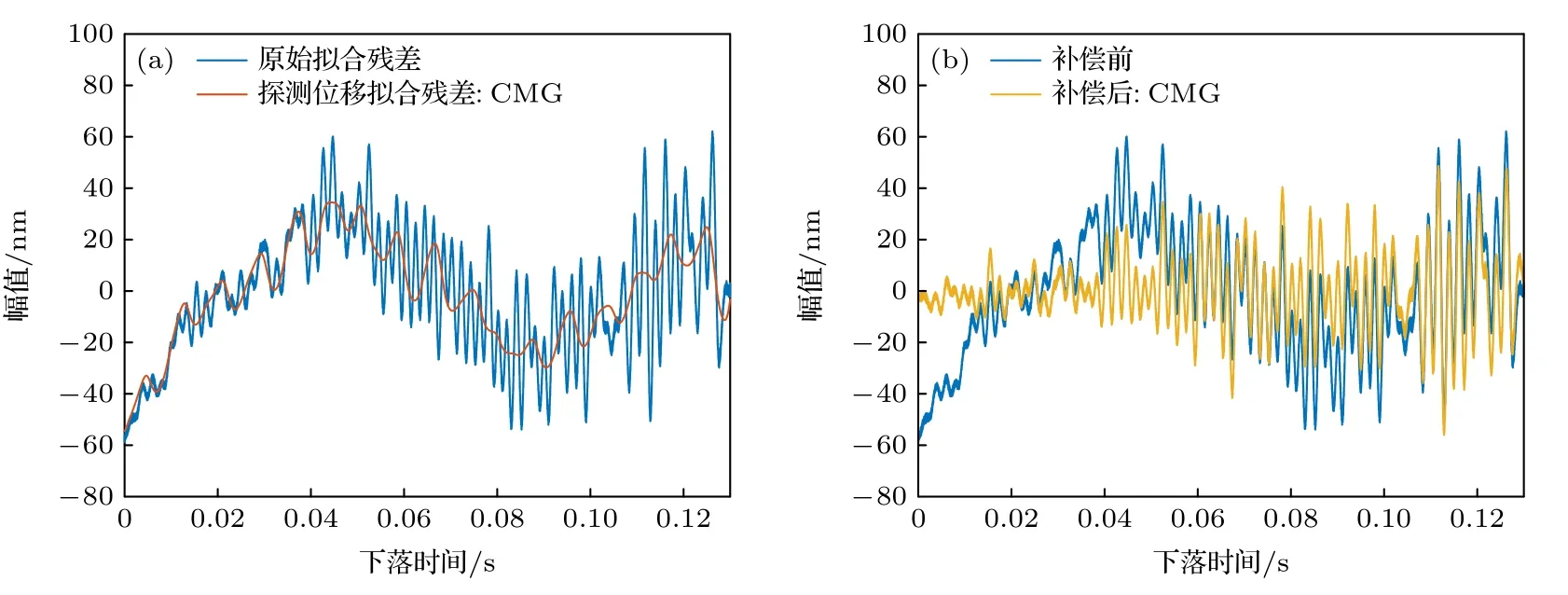
图13 嘈杂地基上CMG 单次补偿的情况 (a)原始拟合残差与探测位移拟合残差对比;(b)补偿前后拟合残差对比Fig.13.Correction for single drop using CMG data on the noisy ground:(a) Residuals of measured trajectory Sm and measured vibration noise Nm;(b) residuals of measured trajectory Sm before and after correction.

图14 嘈杂地基上CS60 单次补偿的情况 (a)原始拟合残差与探测位移拟合残差对比;(b)补偿前后拟合残差对比Fig.14.Correction for single drop using CS60 data on the noisy ground:(a) Residuals of measured trajectory Sm and measured vibration noise Nm;(b) residuals of measured trajectory Sm before and after correction.

图15 嘈杂地基上JN06 D 单次补偿的情况 (a)原始拟合残差与探测位移拟合残差对比;(b)补偿前后拟合残差对比Fig.15.Correction for single drop using JN06 D data on the noisy ground:(a) Residuals of measured trajectory Sm and measured vibration noise Nm;(b) residuals of measured trajectory Sm before and after correction.

对于采用万向悬架作为支撑平台的振动环境，由于万向悬架的稳固性远不如地基，因此万向悬架上的振动噪声在3 种振动环境下最大.图16(a)中幅值高达5000 nm 左右的原始拟合残差反映了万向悬架上的高幅值振动噪声.且该振动噪声存在高度复现性，说明万向悬架上的振动噪声以重力仪系统测量过程中产生的反冲振动为主.在高强度振动环境下，JN06D 型加速度计的分辨率足以实现良好的振动信号探测，如图16(a)所示，JN06D 的探测位移拟合残差与原始拟合残差呈现极高的相关性，补偿后的拟合残差大幅度衰减，补偿后的系统偏差从—1158 mGal 修正到—285 μGal，单次测量标准差也从43 mGal 减小到3.3 mGal.因此动态性能更好的加速度计能在强振动环境下实现毫伽量级的单次测量标准差.

图16 万向悬架上JN06 D 单次补偿的情况 (a)原始拟合残差与探测位移拟合残差对比;(b) 补偿前后拟合残差对比Fig.16.Correction for single drop using JN06 D data on the gimbal:(a) Residuals of the measured trajectory Sm，and the measured vibration noise Nm;(b) residuals of the measured trajectory Sm before and after correction.

进一步分析同一传感器在不同振动环境下补偿性能的变化.对于振动噪声强度小、频率低的安静地基测量环境，CMG 型和CS60 型地震计的分辨率和带宽基本上能满足单次测量标准差优于百微伽的补偿需求，且可以实现接近隔振性能的补偿效果.但随着振动噪声高频成分的增加，受带宽限制，地震计会出现高频信号探测失真现象，从而导致补偿效果下降[13].因此在嘈杂地基的测量环境下，CMG 型和CS60 型地震计的补偿效果均明显下降，由于CMG 的带宽更窄，其补偿效果下降更严重.由此可见，在分辨率满足目标精度的前提下，传感器带宽也是影响补偿效果的重要因素.因此，若要在较复杂的嘈杂振动环境下进一步提高地震计的补偿性能，在保证分辨率的前提下可以考虑提高地震计带宽，如采用数字后校正方法[13]或研制带宽更高的地震计.而对于振动幅值超出地震计量程的万向悬架测量环境，地震计将不再适用.另一方面，JN06D 型加速度计的优点是带宽和量程大，动态性能好，基本上可以覆盖现有野外甚至移动平台重力测量的需求，但受限于其毫伽量级的分辨率.因此，对于以低幅值低频率振动噪声为主的安静地基测量环境，加速度计受分辨率限制而无法实现单次测量标准差优于百微伽的补偿效果.当振动噪声强度增大至毫伽量级以上，加速度计可以实现有效的信号探测，补偿后可以实现毫伽量级的单次测量标准差.而对于超出地震计量程的强振动测量环境，加速度计的补偿效果更加明显，补偿后可以将系统偏差修正1000 mGal 以上，单次测量标准差也改善13 倍.因此，加速度计更适用于地震计无法工作的复杂或动态环境下实现毫伽量级的单次测量标准差.要进一步提高加速度计的补偿性能，则需要在保证其带宽和量程满足需求的前提下提高分辨率，如清华大学研制的采用内置参考棱镜的高分辨率传感器[27].

最后，针对振动补偿领域的传感器选型或传感器设计进行总结.根据前述分析，分辨率、带宽和量程是需要重点关注的传感器参数.因此，在选择合适的传感器时，首先应确认振动补偿的应用环境，包括振动噪声强度和频率成分、以及支撑平台的稳固性，针对应用环境制定合适的目标补偿精度.然后根据应用环境的振动强度筛选量程满足要求的传感器，并选取分辨率优于目标精度的传感器.最后，在分辨率和量程都满足需求的情况下选择在目标频带内传递函数更平坦的传感器，这往往要求更大的带宽.除上述主要参数之外，还可以结合传感器的长期测量稳定性及外形质量等其他参数再综合评估.

5 结论

本文理论分析了传感器性能参数对振动补偿的影响，并通过实验对比研究了不同振动环境下不同传感器的补偿性能.实验结果表明:在安静地基环境下地震计可以实现单次测量标准差优于百微伽的补偿效果，与隔振效果相当，而加速度计受分辨率限制无法实现有效补偿;在嘈杂地基环境下受噪声高频成分增强的影响，地震计的补偿效果下降，补偿后的单次测量标准差增大至百微伽量级，其中带宽更窄的地震计补偿效果下降更明显，加速度计则可以实现单次测量标准差达到毫伽量级的补偿效果;在振动强度更大的万向悬架环境下，地震计由于振动强度接近或超出其量程而无法工作，采用加速度计补偿则可以将系统偏差修正1000 mGal 以上，将单次测量标准差改善13 倍达到毫伽量级.因此分辨率、带宽和量程是影响传感器补偿性能的主要因素.其中地震计的补偿性能主要受带宽和量程的限制，多适用于有稳固地基的环境下实现单次测量标准差优于百微伽的补偿效果，可以通过提高带宽来进一步提高地震计的补偿性能.加速度计的补偿性能则主要受分辨率的限制，多适用于复杂或动态环境下实现毫伽量级的单次测量标准差，可以通过提高分辨率来进一步提高加速度计的补偿性能.此外，结合地震计和加速度计的补偿特性，本文还总结了振动补偿的传感器选型方法，为今后振动补偿领域的传感器选型和设计提供了理论依据.

感谢中国计量科学研究院的重力计量基准与精密测量实验室和原子干涉重力精密测量实验室分别为测试提供测试场地和CMG 型地震计.