感性神经元模型及其动力学特性研究

吴静 潘春宇

(北京航空航天大学自动化科学与电气工程学院，北京 100191)

神经元的大小属于介观尺度范围，本文考虑神经元的电感特性，建立了由细胞膜电感、膜电容、钾离子忆阻器和氯离子电阻构成的神经元经典电路模型和介观电路模型.利用经典电路理论和介观电路的量子理论，推导了在外部冲击激励下神经元细胞膜电压响应的表达式.将枪乌贼神经元的电生理参数代入膜电压表达式并计算可知，两种模型下的膜电压均先增大后减小，最后达到零值的静息状态，且其能量主要集中在0—30 Hz 的脑电频率范围内.进一步比较发现，介观电路模型下膜电压的峰值及达到峰值所需的时间(达峰时间)均低于经典电路模型下的值，并与枪乌贼轴突受到刺激后的实验结果更接近，说明介观电路模型更能反应神经元受到刺激后的生理特征.基于介观电路模型，随着外部激励强度的增加，膜电压的峰值增加且达峰时间变短.膜电压峰值及达峰时间等参数更易受神经元膜电容的影响.神经元的介观电路模型对于理解神经元受到刺激后的兴奋性，推动受大脑功能启发的量子神经网络的发展等具有重要意义.

1 引言

上千亿神经元形成了记忆、学习和智能等高级认知活动的物质基础.神经元建模可以分为电导依赖型和非电导依赖型两类[1].前者研究神经元及其网络的电学生理特性和动力学行为，如Hodgkin-Huxley(HH)模型[2-5].后者在前者的基础上，抛开电路参数的实际意义，利用纯数学模型研究神经元输入和输出之间的关系，阐明信息传递的机制，主要用于神经形态计算和神经接口的信息处理等[6-8].

神经元的大小为微米量级，属于介观尺度范围[9，10].为了能够反映神经系统的纠缠、叠加等量子特性对其生理特性及信息传递机制的影响，有必要研究电导依赖型神经元的量子化模型.作为被广泛研究的电导依赖型模型，HH 模型是通过枪乌贼轴突实验提出的，由可变离子(如K+和Na+)电导、恒定离子(如Cl—)电阻及细胞膜电容组成[5].Chua[11]考虑了神经元对电荷的记忆特性，将可变离子电导进一步利用可变离子忆阻器表征.基于经典电路理论，HH 模型及其构成的神经网络模型在探索疾病机理[12-14]、神经网络的集体行为[15-17]和理解大脑功能[18-20]等方面有着广泛应用.如Khodashenas 等[12]利用HH 模型研究了经颅直流电刺激对三叉神经痛的缓解作用.Liu 等[13]讨论了经颅磁声刺激下HH 神经元网络的同步动力学，并通过设计自适应控制器使神经元满足同步性能.Zhang 等[14]讨论了通过忆阻器耦合的HH 神经元网络在外界高频刺激下动作电位传导失效的影响因素.Bao 等[15]研究了HH 神经元网络非相干、相干、不完全同步和嵌合状态等动力学行为.Baysal 等[16]研究了输入混沌信号对HH 模型弱信号检测性能的影响.Bossy 等[17]研究了无限个HH 模型完全连接的神经元网络动作电位的同步特性.文献[18，19]研究了HH 模型能量供应和消耗特性，提出了HH 模型在超阈值和亚阈值激活时能量消耗的判据，结果表明神经元的电生理活动受到其能量水平的严格限制.Zhu 等[20]利用神经元能量编码理论研究了HH 网络模型的神经活动，结果表明网络能量分布的周期性与神经元数量和耦合强度呈正相关，但与信号传输延迟呈负相关.基于介观电路的量子理论，量子化忆阻器以及它在超导电路和集成量子光学中的实现，为量子化HH 模型提供了理论和实验基础[21-23].近年来，Gonzalez-Raya 等[24]研究了考虑K+忆阻器的量子化HH 模型，得到了在正弦激励下细胞膜电压输出响应的量子化特征，对于构建受大脑功能启发的量子神经网络和量子机器学习具有重要意义[25-27].

已有经典和量子化HH 模型并没有考虑神经元的电感特性.Cole 和Baker[28]在乌贼轴突上利用阻抗桥进行了纵向交流阻抗的测量，发现细胞膜在低频时具有感抗特性.Hodgkin[29]认为在青蛙肌肉、乌贼和鱿鱼轴突实验中观察到的阈下膜电位振荡现象是由于细胞膜电感和膜电容并联所导致的.Kumai[30]认为神经元实验中的阳极断开兴奋和超极化断开刺激都说明细胞膜电感的存在.不仅如此，Wang 等[31]研究神经元的能量编码时，利用电感表征神经元产生动作电位时离子内外流动形成的磁场.周霆[32]认为大脑皮层中的锥体细胞并行排列，方向垂直于脑皮质层表面且沿径向分布，一定数量神经元的同步活动形成了以电流偶极子为特征的生理学基础，表明神经元中存在磁场效应.因此，在利用神经元等效电路研究其动力学特征时，有必要在电路模型中引入细胞膜电感.

本文仅考虑神经元可变离子K+和恒定离子Cl—，利用细胞膜电感、膜电容、K+忆阻器和Cl—电阻建立了感性神经元电路模型，研究了基于经典电路理论和介观电路量子理论的电路分析方法，对比了在冲击激励下利用两种方法得到的膜电压输出响应的特点.

2 感性神经元模型

2.1 经典电路模型

神经元是神经系统最基本的结构和功能单元，由接受外部刺激的树突、整合输入信息的胞体和传递输出信息的轴突组成，如图1(a)所示，考虑细胞膜电感特性的电路模型如图1(b)所示.其中，L表示细胞膜电感;R为恒定渗漏通道(主要为Cl—)的电阻;C为细胞膜电容;Cg为神经元与外部耦合的树突电容;G为可变离子K+通道忆阻器.根据文献[24]，忆阻器G的特性可表示为G(n(t))gK[n(t)]4，这里gK为K+通道的最大电导，n(t)表示K+离子通道的激活概率，其与神经元细胞膜电压V(t)有关:

图1 神经元及其电路模型 (a) 神经元的结构;(b) 感性神经元的经典电路模型Fig.1.Neuron and its circuit model:(a) Structure of the neuron;(b) classical circuit model of the inductive neuron.

其中αn(V(t))0.01[10-V(t)]/[e[10-V(t)]/10-1]，βn(V(t))0.125e-[V(t)/80].

假设电路在幅值为I的外部冲击电流Iext(t)=Iδ(t)的作用下，流过电感的电流为IL(t)，对于节点A，根据基尔霍夫电流定律以及Dirac 函数δ(t)的特点，可得

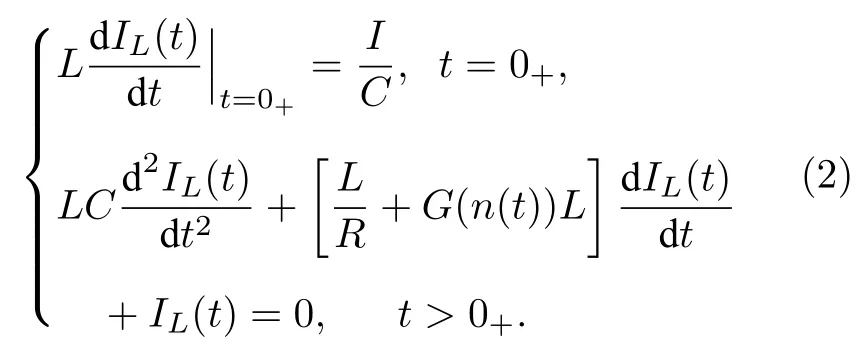
上式中只要知道膜电感L、膜电容C、恒定渗漏通道的电阻R、可变离子通道忆阻器的电导G以及外部冲击电流的幅值I，便可以通过数值方法求解膜电感电流IL(t)，然后利用V(t)=LdIL(t)/dt得到膜电压.

2.2 量子化电路模型

为了研究感性神经元介观电路模型的量子化特性，需要对介观电路模型进行正则量子化.然而，当存在电阻和忆阻器等耗散元件时，正则量子化中的拉格朗日方程不满足时间可逆性和平移对称性.为了解决该问题，利用由电感和电容组成的Caldeira-Leggett 谐振子电路模型[33]来描述介观系统在耗散过程下的动力学特征.以节点A为原点，以流经忆阻器的电流为x轴正方向，分别将忆阻器G和电阻R用M和N个长度为Δxm和Δxn的Caldeira-Leggett 谐振子等效电路代替，得到感性神经元的介观电路模型如图2 所示.其中，φm(t)，c0(t)和l0(t)分别为忆阻器等效电路中第m个节点磁通、单位长度的电容和电感;(t)，c1(t)和l1(t)为电阻等效电路中第n个节点磁通、单位长度的电容和电感;φ0(t)为节点A处的磁通;φs(t)为激励源处的节点磁通.取x=0 处的φ0(t)作为广义坐标，则系统的拉格朗日量为

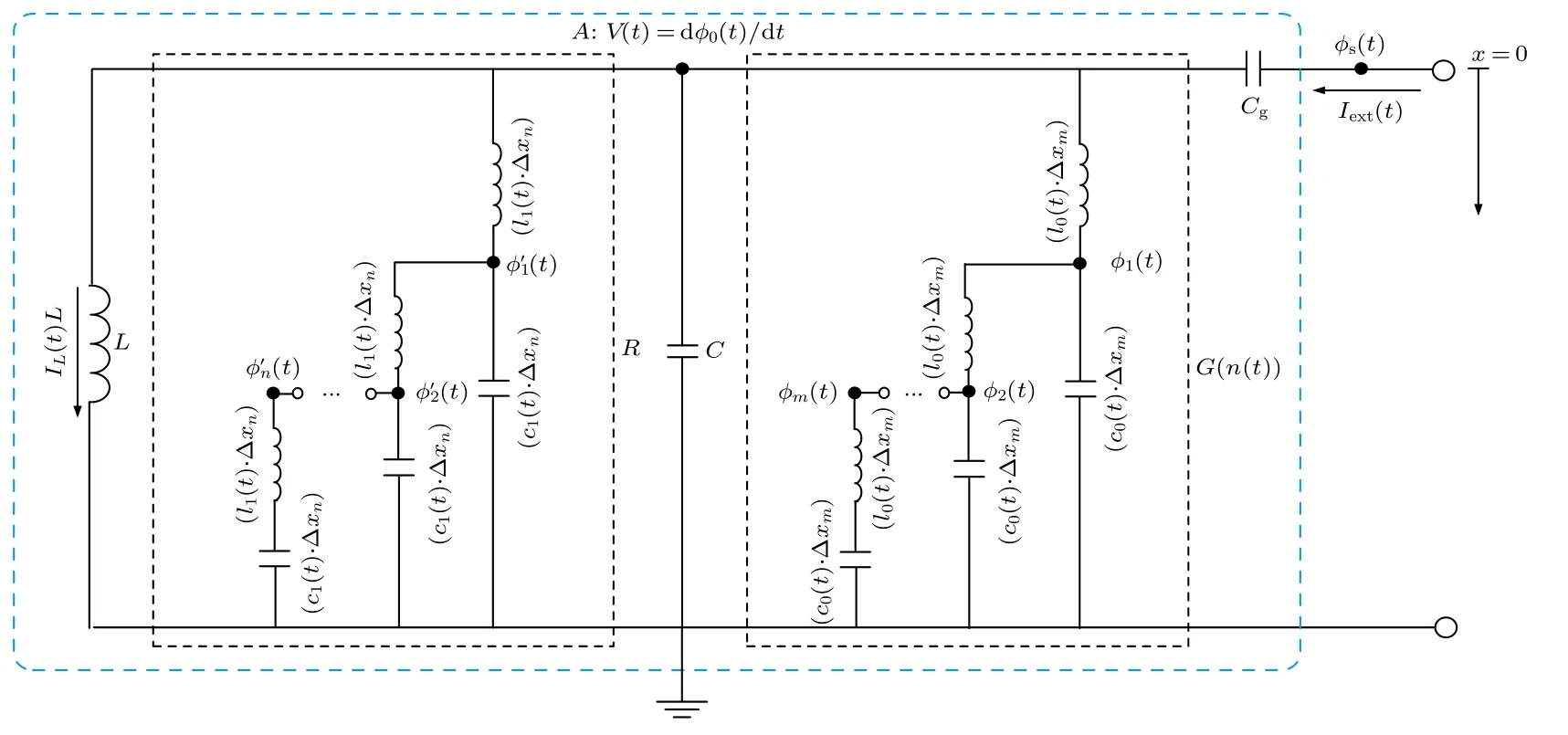
图2 感性神经元的介观电路模型Fig.2.Mesoscopic circuit model of the inductive neuron.

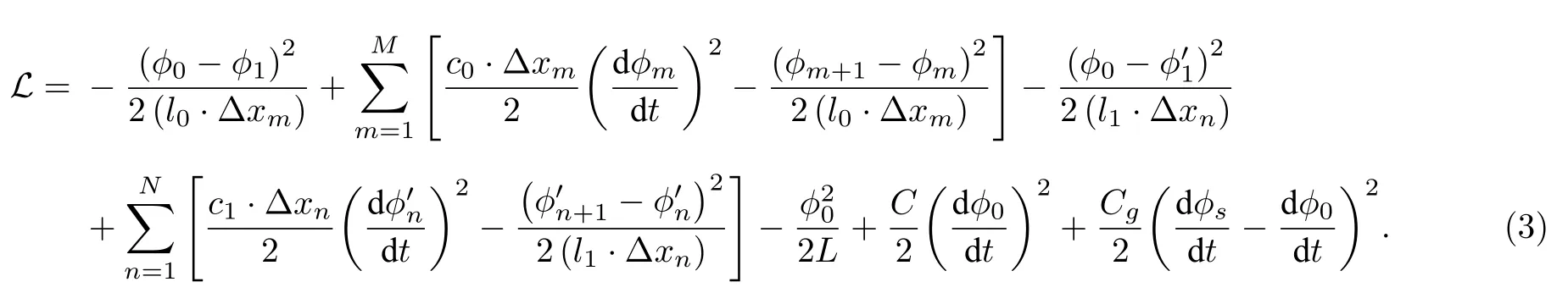
此时外部激励可以表示为Iext(t)Cg(d2φs/dt2-d2φ0/dt2).这里φ0(t)可利用输入波函数φin(t)表示为[24]

联立(6)式和(7)式，可得

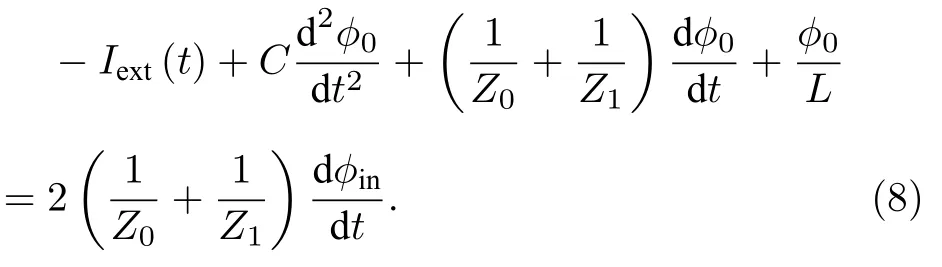
忽略节点磁通φ0(t)的高频分量，其量子化分解为

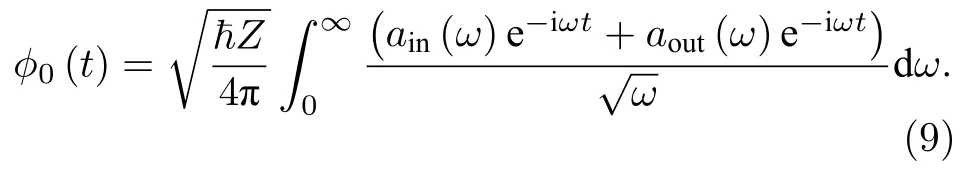
将外部输入电流Iext(t)在频域分解为

联立(8)式、(9)式和(10)式，输出量子湮灭算符可用输入量子湮灭算符表示为

其中 I m[·]表 示取函数的虚部;f(t)的表达式为

在感性神经元的经典电路模型中，根据IL(t)φ0(t)/L，利用KCL 可得

其中G=1/Z0，R=Z1.对比(8)式和(14)式，当dφin(t)/dt0时，介观电路和经典电路模型的表达式相同.根据

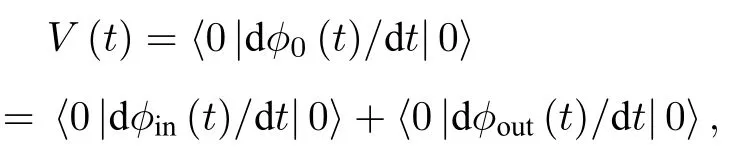
当考虑真空态时，〈0|ain(ω)|0〉0，〈0|φin(t)|0〉0，V(t)〈0|dφout(t)/dt|0〉，介观电路中的细胞膜电压将低于经典电路中的值.从物理意义上，在神经元介观电路中，磁通的波动性不可以忽略，当电路的尺度增大至宏观尺度时，波动性可以忽略，即dφin(t)/dt0，此时介观电路模型可以转化为经典电路模型.

3 分 析

对于经典和介观电路模型，选取与文献[5]和文献[28]相同的枪乌贼神经元参数:C=1 μF，L=200 mH，Z0=1/G(n(t))=1/[gKn(t)4]，gK=36 mS，Z1=R=400 Ω，由于感性神经元介观电路模型的膜电压响应表达式中静息电位并不出现，简单起见，在经典电路和介观电路模型中均取静息电位为0，这样并不会改变神经元的动力学响应，只会使膜电压响应发生偏移.参考文献[24]以及本文所提方法，在幅值为1 mA 的外部冲击激励下，可以分别得到传统HH 单离子通道神经元以及本文感性神经元在经典电路模型和介观电路模型中膜电压V(t)和K+电导G(t)的响应，如图3 所示.由图3(a)和图3(b)可见，传统HH 单离子通道神经元在经典和介观电路模型下的膜电压均会先瞬间达到峰值，最后逐渐减小至零值的静息状态;K+电导的稳定值都在0.40 mS 附近.在经典电路模型中，膜电压峰值为Vp-c=1000 mV，而在介观电路模型中，膜电压峰值为Vp-m=863 mV.神经元接受刺激时，动作电位会先上升发生去极化过程，然后会逐渐下降经历复极化过程，传统HH 单离子通道神经元的经典电路和介观电路模型都不能反映这一特征.由图3(c)和图3(d)可见，感性神经元在经典电路和介观电路模型下的膜电压都会先增大后减小，最后达到零值的静息状态，能反应神经元受刺激后的动作电位变化特征.两种模型下的K+电导的稳定值都在0.40 mS 附近.在经典电路模型中，膜电压达到峰值Vp-c=226.90 mV 所需的时间为Tr-c=0.52 ms.而介观电路模型中，膜电压达到峰值Vp-m=119.94 mV 所需的时间为Tr-m=0.29 ms，这与实验中枪乌贼轴突在受到刺激后膜电压达到峰值96.80 mV 所需的时间0.28 ms[5]更接近，说明考虑细胞膜电感、可变离子通道的忆阻器特征时，利用介观电路模型更能反应神经元的动力学行为.

图3 冲击输入下神经元的动力学响应 (a)，(b) 分别为传统HH 单离子通道神经元经典和介观电路模型下膜电压(蓝色)和K+电导(红色)随时间变化的曲线;(c)，(d) 分别为感性神经元经典和介观电路模型下膜电压(蓝色)和K+电导(红色)随时间变化的曲线;(e)，(f) 分别为感性神经元经典和介观电路模型下膜电压的时频功率密度谱图Fig.3.Dynamic response of a neuron under impulse input:(a)，(b) The curves of membrane voltage (blue) and K+ conductivity(red) versus time obtained by solving classical and mesoscopic circuit models of the traditional HH single ion-channel neuron，respectively;(c)，(d) the curves of membrane voltage (blue) and K+ conductivity (red) versus time obtained by solving the classical and mesoscopic circuit models of the inductive neuron，respectively;(e)，(f) the time-frequency spectrogram of the membrane voltage obtained by solving the classical and mesoscopic circuit models of the inductive neuron，respectively.

图3(e)和图3(f)分别为经典和介观电路模型下对膜电压进行短时傅里叶变换后的时频图.从图3(e)和图3(f)中可以看出，神经元受到刺激后的能量主要集中在0—30 Hz 的频段，与人的脑电频率范围一致.两种电路模型中各频率分量的功率谱密度先增大后减小.在经典电路模型中，各频率分量在t=0.53 ms 时达到能量最大值;功率谱密度的范围为580—1160 mV2/Hz;各频率分量的功率谱密度在t=7.30 ms 时衰减为1 mV2/Hz.在介观电路模型中，各频率分量在t=0.29 ms 时达到能量最大值;功率谱密度的最大值在161.3—322.5 mV2/Hz 的范围内;各频率分量的功率谱密度在t=1.14 ms 时衰减为1 mV2/Hz.这表明当考虑神经元的量子特性时，神经元受刺激后低频段的能量并不高，并且持续的时间更短.

由于膜电压峰值及达峰时间可在一定程度上衡量神经元对外部刺激的兴奋程度和响应速度[34]，以下基于感性神经元介观电路模型，研究膜电压峰值及达峰时间与外部激励的强度、神经元内部参数的关系.取L=200 mH 和C=1 μF，绘出Vp-m和Tr-m随I和R的变化曲线如图4(a)和图4(b)所示;取R=400 Ω 和C=1 μF，绘出Vp-m和Tr-m随I和L的变化曲线如图4(c)和图4(d)所示;取R=400 Ω 和L=200 mH，绘出Vp-m和Tr-m随I和C的变化曲线如图4(e)和图4(f)所示.由图4可见，随着外部激励强度I的增加，Vp-m将增大，而Tr-m将减小，这说明外部刺激的增强会使神经元在更短的时间内达到更高的兴奋度.另外，Vp-m随着R的增大而逐渐增大到某稳定值;随着L和C的增大而逐渐减小到某稳定值.Tr-m随着R，L和C的增大而逐渐增大到某稳定值.这里将dVp-m/dR，dVp-m/dL，dVp-m/dC，dTr-m/dR，dTr-m/dL和dTr-m/dC定义为膜电压峰值及达峰时间对神经元内部参数的灵敏度，表1 给出了各参数灵敏度的计算结果.当I相同时，Vp-m和Tr-m对C的变化最灵敏，对R的变化最不灵敏;随着I的增加，Vp-m对R，L和C的灵敏度均增大，Tr-m对R，L和C的灵敏度均减小.以上结果说明，神经元受刺激后，其兴奋程度和响应速度最容易受膜电容的影响;随着外部刺激增强，神经元内部参数对神经元兴奋程度的影响越大，对响应速度的影响越小.

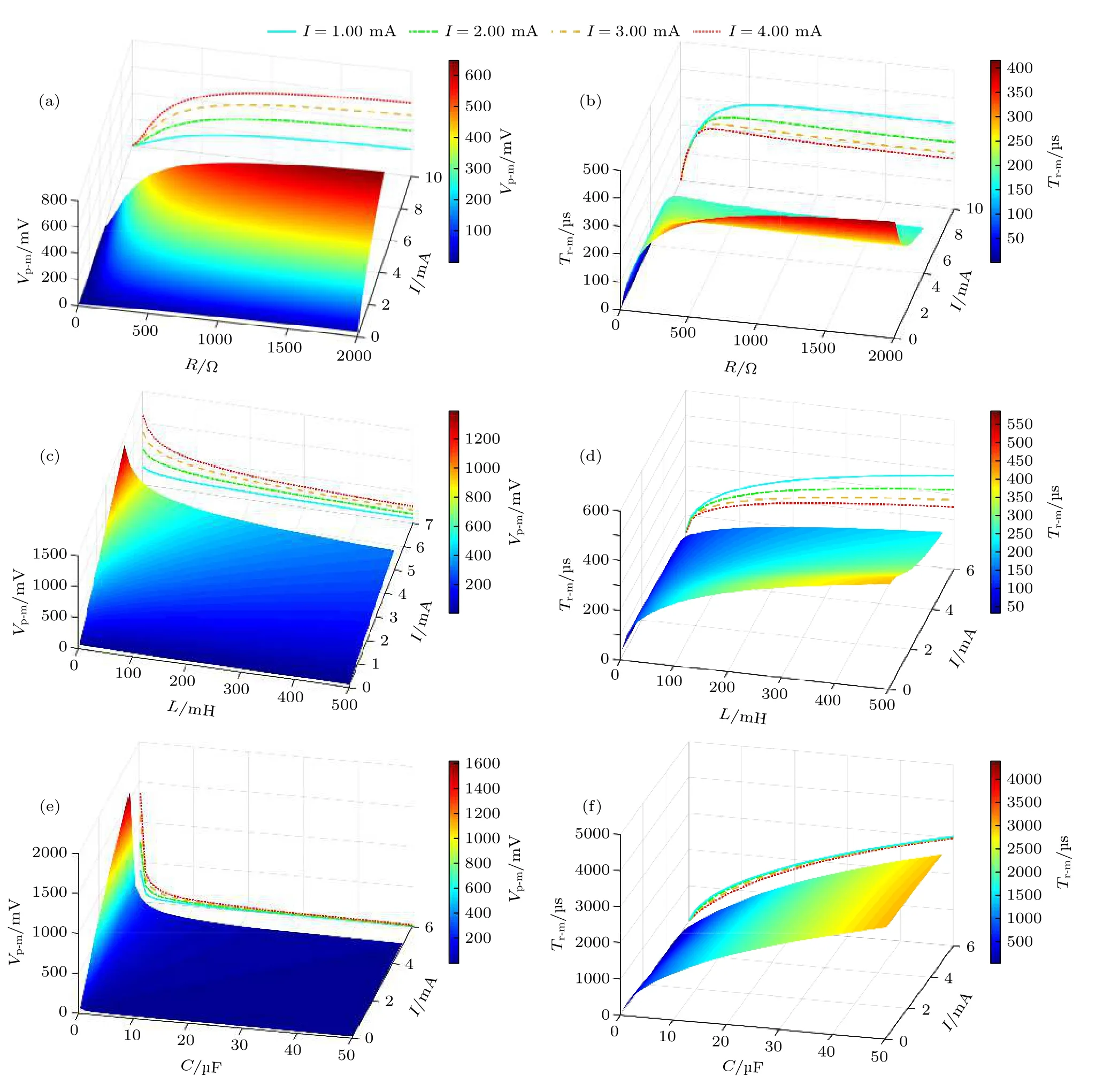
图4 感性神经元介观电路模型中膜电压输出响应与外部激励和神经元内部参数的关系 (a)，(c)，(e) 分别为Vp-m 随I，R，L 和C 的变化曲线;(b)，(d)，(f)分别为Tr-m 随I，R，L 和C 的变化曲线Fig.4.The relationship between the output response of the membrane voltage in the mesoscopic circuit model of inductive neuron and the external excitation and the internal parameters of the neuron:(a)，(c)，(e) The dependence curves of Vp-m on I，R，L and C，respectively;(b)，(d)，(f) the dependence curves of Tr-m on I，R，L and C，respectively.

表1 感性神经元的Vp-m 和Tr-m 对神经元内部参数的灵敏度Table 1.Sensitivity of Vp-m and Tr-m of the inductive neuron to the internal parameters.

4 结论

本文利用神经元细胞膜电感、膜电容、K+忆阻器和Cl—电阻建立了经典电路模型;利用由电感和电容组成的Caldeira-Leggett 谐振子表征K+忆阻器和Cl—电阻在耗散过程下的动力学特征，建立了神经元介观电路模型.研究了神经元介观电路中膜电压的量子化分析方法，即首先将节点磁通选为广义坐标，利用Euler-Lagrange 方程求出在外部激励下节点磁通随时间的变化方程;然后，对节点磁通进行量子化分解;最后，利用节点磁通对时间的导数计算出膜电压.

对比分析了经典电路模型和介观电路模型在外部冲击激励下，细胞膜电压和K+电导的响应特性.结果表明，两种模型下膜电压均先增大后减小，最后达到零值的静息状态，且能量主要集中在与脑电频率接近的范围内.相较于经典电路模型，利用介观电路模型得到的反应神经元受刺激后兴奋度的膜电压峰值较低，达到峰值所需的时间也较短，与枪乌贼轴突的实验结果基本一致.基于对神经元介观电路模型的分析可知，随着外部刺激的增强，神经元能在更短的时间达到更兴奋的状态;神经元膜电压响应对膜电容的变化最为灵敏，对恒定离子电阻的变化较不灵敏.神经元介观电路模型对于推动脑科学朝定量、精确和理论化体系发展，弄清人脑功能的机理，建立人类认知过程的微结构理论等具有重要意义.