均质细直杆在光滑半圆槽内运动的研究
罗 正
(北京理工大学精工书院 北京 102488)
1 提出问题
小球在光滑半圆槽内的运动是讲解动量守恒时常用的模型.如果将小球换成均质细直杆,那么对于均质细直杆的运动就无法用质点运动学的知识进行求解.均质细直杆是刚体,刚体运动因具有角速度而有别于质点运动,所以需要应用刚体运动学和动力学的相关知识进行推导.本文将以如下题目为例,通过两种方法求解均质细直杆在光滑半圆槽内的运动.
在图1所示的竖直平面内,质量m1=3m,半径为r的光滑半圆槽放置在光滑水平面上,其中放置有质量m2=m,长度为r的均质细直杆AB,初始时刻A端位于半圆槽左顶点处.系统无初速度释放,求杆AB发生30°转角的瞬间,杆AB的角速度.
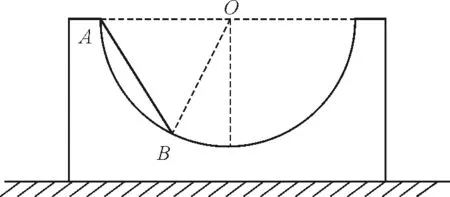
图1 半圆槽-均质细杆系统
2 用动量守恒和机械能守恒求解杆AB的角速度
如图2所示,半圆槽沿水平方向做直线运动,杆AB的质心C相对于半圆槽以动点O为圆心做圆周运动.
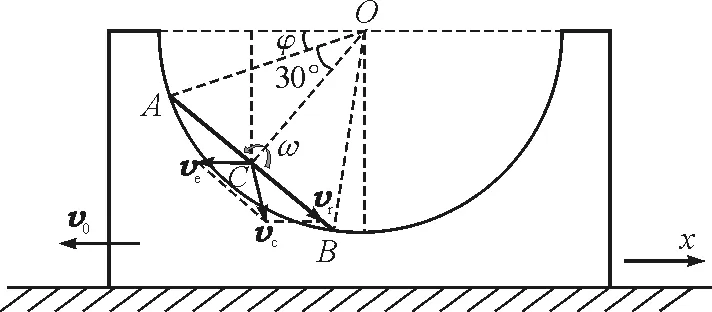
图2 速度分析
设质心C的速度为vc,半圆槽速度为v0,质心C相对于半圆槽的速度为vr.以半圆槽为参考系,选取质心C为动点,根据伽利略速度变换有
vc=v0+vr
(1)

m1v1x+m2vcx=0
有
(2)
整理得
(3)
在系统运动的过程中,只有杆AB的重力做功,所以系统的机械能守恒.初始时刻系统的动能T0=0,末了时刻系统的动能为
(4)
设半圆槽最低点,也即末了时刻杆AB上B点所在的位置为零势能点.则初始时刻系统的势能
末了时刻系统的势能
根据机械能守恒定律
T0+V0=T1+V1
有
(5)
根据系统末了时刻的运动状态,可知杆AB沿逆时针方向转动,角速度方向垂直纸面向外.化简式(5),角速度大小为
(6)
3 用瞬时法求解杆AB的角速度
上一节给出了用动量守恒和机械能守恒求解杆AB角速度的方法.本节将从系统运动瞬时状态的角度切入,给出此题的另一种解法.
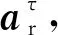
(7)
其中
ω和α分别为杆AB的角速度和角加速度.杆AB的转动角度为φ时,假定各加速度方向如图3所示.

图3 加速度分析
在系统运动的过程中,半圆槽和杆AB组成的系统在水平方向不受外力,根据质心运动定理可知
(8)
整理得
(9)
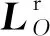
(10)
杆AB的重力对动点O产生的力矩MO为
(11)
对杆AB使用相对动点O的动量矩定理
在垂直纸面方向上投影得到标量方程
(12)
(13)
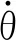
(14)
将式(14)代入式(13),整理得
(15)
考察式(15)发现,等式左侧可以合并为
即
(16)
(17)
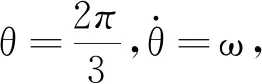
4 基于MATLAB的数值模拟
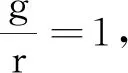

图5 ω-t曲线


(18)


图6 运动周期随质量比的变化曲线
5 结束语
本文通过两种方法解出了例题中杆AB的角速度,利用MATLAB数值模拟清晰直观地分析了系统的周期性运动,又讨论了半圆槽与均质细直杆的质量比对系统运动周期的影响,给出了均质细直杆在光滑半圆槽内运动的综合性研究.

