卡方校正算法对入侵检测特征选择的优化

刘 云，郑文凤，张 轶

昆明理工大学信息工程与自动化学院，云南 昆明 650500

0 引言

数据特征选择在大数据挖掘和分析及机器学习等领域都有广泛应用，尤其在入侵检测系统（intrusion detection system，IDS）中，选择重要数据特征是识别网络攻击准确性的关键因素［1］。为了给分类模型构建高效的特征选择（feature selection，FS）算法，通常用基于互信息（mutual information，MI）的方法学习和估算高维数据特征的重要性，该方法可以快速找到数据特征中的相关信息，选择出最大相关最小冗余（maximum relevance minimum redundancy，mRMR）的 特 征子集［2，3］。

Wang等［4］结合数据特征的关联性，构建了互信息增益最大化（mutual information gain maximize，MIGM）算法，通过等效分区概率对特征数据进行划分，并用最大联合互信息准则对候选特征进行评估。该方法可以快速识别有效的特征子集，比传统方法具有更好的适用性。Wei等［5］根据动态特征重要性（dynamic feature importance，DFI）指标，提出基于MI的动态特征重要性特征选择（M-dynamic feature importance based feature selection，MDFIFS）算法，使用最大信息系数有效排除冗余特征，再通过随机森林的基尼系数选出重要特征，所选的特征数据与类要素之间有更强的相关性。但是这些方法都没有考虑信息熵的偏差校正。

为了在入侵检测系统中减少信息熵偏差对分类性能的影响，构建实时可靠的IDS，本文提出了卡方校正算法（chi-square correction algorithm，CSCA）。首先对所有候选特征进行离散化处理，根据特征的潜在概率分布估计特征选择相关标准的偏差；然后，通过考虑偏差的目标函数得到特征选择的临界值；最后，通过χ2检验优化离散化水平和特征偏差，更新特征子集。

1 入侵检测特征选择

1.1 入侵检测特征选择模型

选择重要相关的特征并及时做出数据更新对IDS防御攻击非常重要。特征选择的目的就是在所有候选特征集F中选出最优特征子集f={f1，f2，…，fs}，为分类模型提供在类之间具有最大区分力的特征数据，并降低数据维度［6］。针对高维数据流中存在的特征变化，基于MI的特征选择方法可减少无关特征和冗余特征对模型的影响。

为了简化特征数据，通常在特征选择之前把连续值的特征转换为离散特征。在图1入侵检测模型中，将数据流中提取的特征和训练后的标准特征动态离散化为n个区间，则离散化间隔为{[d0，d1]，…，[d n-1，d n]}，特征fi的最小值为d0，最大值为d n，d i s是间隔点。特征离散化可能存在信息丢失，但可以减少数据噪声，增加模型的稳定性和分类准确性［7］。

图1 入侵检测的特征选择模型Fig.1 Feature selection model for intrusion detection

数据特征离散化后，通过特征选择的标准为分类器选择最优特征子集，并将该特征子集更新为下一次检测的候选特征。最后使用支持向量机（sup⁃port vector machines，SVM）分类模型检测攻击，SVM有效减少了数据维度的影响，有较高的分类精度［8］。

为了独立于分类算法并降低计算成本，一般构建基于MI过滤的特征选择方法评估特征。MI方法能够测量随机变量之间的非线性依赖关系，评估复杂分类任务中数据特征的信息内容［9］。两个变量的MI通常用熵表示，熵为信息不确定性的度量，计算形式如下I(X;Y)=H(X)+H(Y)-H(X,Y)（1）其中，H(X)和H(Y)为边际熵；H(X，Y)为联合熵，为变量X和Y平均所需要的信息量。若X是连续型随机变量，则f（x）表示X的概率分布函数。若用N个等长Δx分隔X，则第i个间隔中观测样本的概率值pi=∫f(x)dx≈f(x i)Δx，假设f（x）在一个区间内近似恒定，熵的近似值如下

其中，N表示总的样本数，ni为第i个间隔的观测样本

1.2 特征选择标准

假设一组数据集中有K个特征数据和M个数据类别，用互信息I(f;C)表示特征数据中包含的关于目标类别C的信息量，从最大化下式

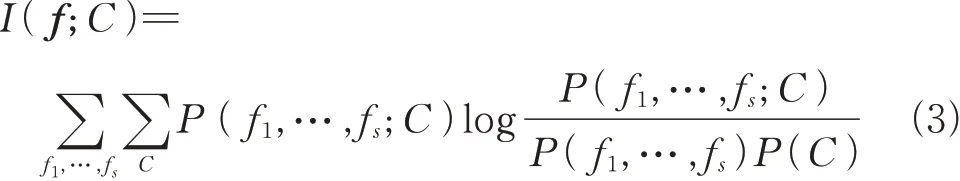
可以得到特征子集f的最小集合。

为了减少I(f;C)的计算成本，通过联合互信息（joint mutual information，JMI）方法［10］选择第i个特征fi的模型如下式

通过最大化（4）式得到特征选择标准的最优值，即最大特征的相关性R、最小的特征冗余r和最大特征的互补信息CI，根据这三个标准可以选择当前最重要的特征。用潜在的概率分布估计特征熵时会引入偏差，假设样本ni是多项式独立分布的，根据概率函数在处的泰勒级数，样本期望为

N是变量X中的离散间隔数，观测样本的期望和方差如（7）式

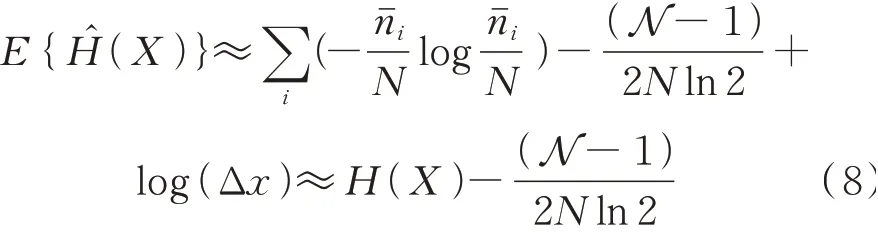
将变量Y分为J个间隔可用下式表示

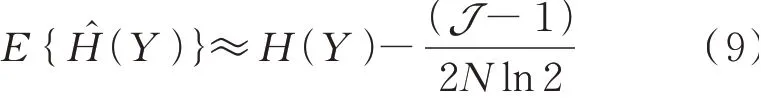
若x-y平面被分为N×J个大小相等（Δx×Δy）的单元，则变量X和Y联合熵的期望为

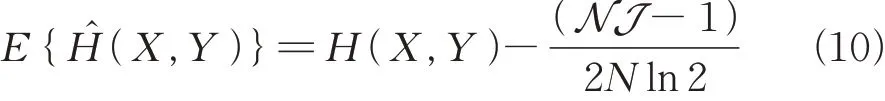
结合式（1）可以得到

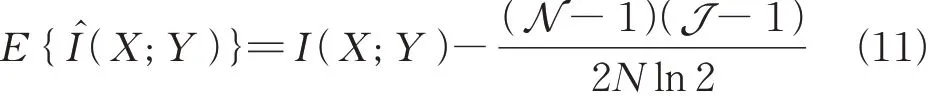
根据两个连续随机变量熵的期望，可以看到互信息I(X；Y)的偏差是

2 卡方校正算法(CSCA)

2.1 偏差校正

根据MI计算信息熵中存在的偏差会对特征选择产生影响，因此需要进行偏差校正。设存在有N个间隔的连续随机变量X和离散的类变量C，K表示类别C的个数，X和C的MI用信息熵表示为

结合（8）式，假设给定X的信息熵是一个固定值，用代 替用估 计p(c)，则（12）式可写为

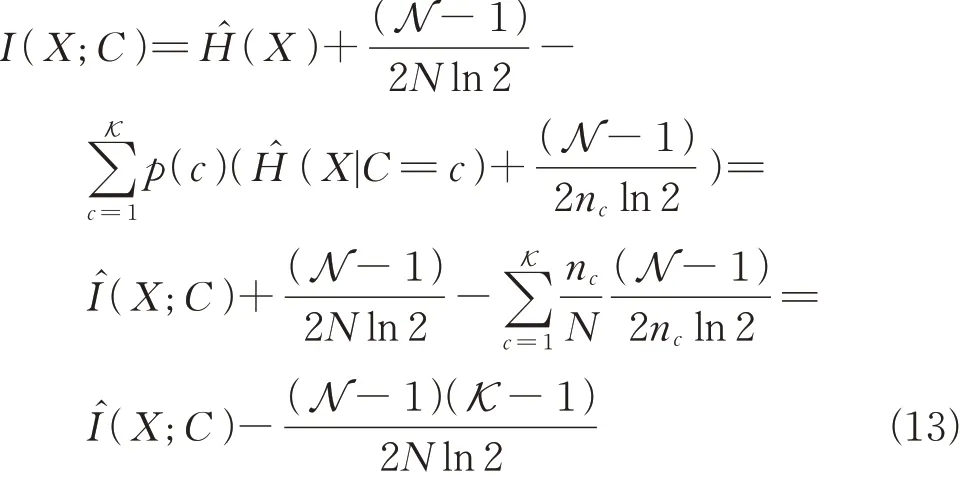
由此可以看到I(X；C)和I(X；Y)产生的偏差是 相 似 的，同 理 可 得I(fi；C)，I(f i；fj)的 偏 差。因此，

若N和J是特征fi和fj中的间隔数，可以得到I(fi;fj|C)的偏差是此时，在（4）式的目标函数中添加偏差项为

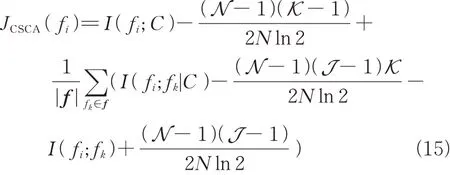
添加偏差后的目标函数有助于准确计算JMI，分别对R，r和CI进行偏差校正，选出最优的特征子集。

由（15）式可以发现，当fi和C统计独立时，相关性I(fi;C)服从自由度为(N-1)(K-1)的χ2分布。当fi和fj统计独立时，冗余I(f i;fj)服从自由度为(N-1)(J-1)的χ2分布。临界值和分别如下

同理若给定变量Z，两个独立随机变量X和Y的条件互信息为

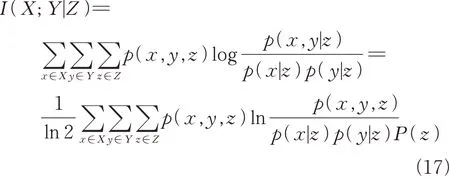
其中，p(x，y，z)是联合概率，p(x|z)和p(y|z)是条件概率。假设q(x，y，z)≡p(x|z)p(y|z)p(z)，则有

令p1=p(x，y，z)，q1=q(x，y，z)，则f(p1)=时泰勒展开，展开式第三项简化为并忽略高阶项，得到下式

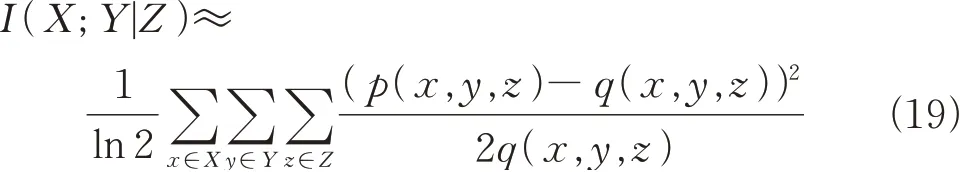
将（19）式化为标准表达式后，I(X；Y|Z)服从自由度为(|X|-1)(|Y|-1)Z的χ2分布。因此，对于给定类别C且在fi和C统计独立的情况下，I(f i;fj|C)服从自由度为(N-1)(J-1)K的χ2分布。的计算如下

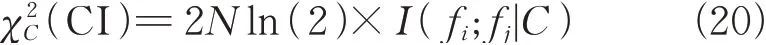
由于特征数据的R，r和CI都服从χ2分布，将χ2分布同时用于检验离散化和特征选择，可以减少离散化的信息丢失，同时优化偏差得到最优目标函数［12］。因此，通过比较（15）式、（16）式和（20）式的临界值，可以做出特征选择和离散化水平决策。

2.2 算法实现及评估指标

首先，CSCA算法使用类信息C计算其MI，根据其相关性分别计算每个特征的离散度

其中，f d i i表示特征fi的离散化水平为d i，算法用χ2分布检验离散化可以选择最小的d i，即根据特征对类别C的依赖，每个特征中不同值的总数可以确定最大离散间隔d。因此，不同特征值有不同的离散间隔。但是，为了在最大的d内实现特征数据最佳的离散化水平，对所有特征使用相同的间隔。离散化水平设置和特征选择的主要步骤如算法1。

?

在算法1中，训练得到的特征按照相关性降序排序，选出相关性高的特征向量。为了使选择的特征和类变量C的联合性更加相关，通过偏移少量的δ改变新特征的离散化水平，若偏移过大则使特征数据将变得不相关。算法在JCSCA大于特征选择标准的临界值时，数据特征被选择。

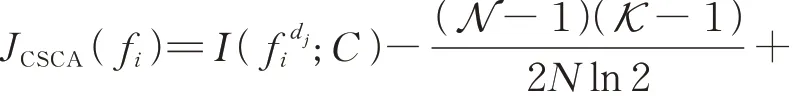
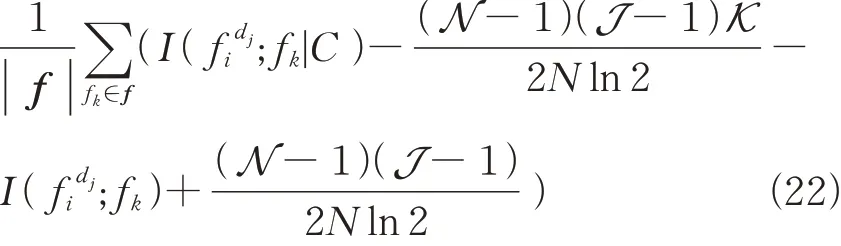
通过算法1检验所有特征的R，r和CI来评估特征的重要程度，若某个特征的r高，则丢弃，若R和CI有意义，则选择该特征，最终可得到适当离散程度的最优特征子集。

CSCA在应对高维数据特征时，可以筛选出重要相关的约简特征，提高IDS的检测准确性。为了评估算法的性能，使用准确率（A）、召回率（R）、查准率（P）和误报率来衡量IDS的优劣。

准确率为正确分类的样本数占总样本的比例，计算如下

召回率表示被正确分类的样本中正常数据所占的比例，计算如下

查准率表示预测为正确的样本数中，正确分类数据的占比，计算如下

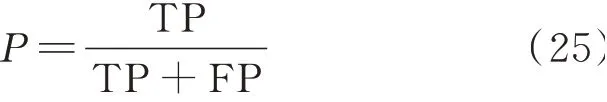
以上式子中，TP表示准确分类正常数据的样本数，FP表示正常的数据中存在误报的样本数，TN表示准确分类攻击数据的样本数，FN表示攻击数据中被漏报的样本数［5，13］。

实际数据中R和P指标不会都达到理想值，需要加权调和平均F1值进行综合考虑，计算如下

误报率是将正常的样本数据预测为攻击类别所占的比例，计算公式如下

高性能的IDS一定是低误报率。

3 仿真分析

3.1 数据集及仿真环境

为了研究数据特征选择的影响，选用两个常用的基准数据库NSL-KDD数据集［14］和UNSWNB15数据集［15］进行实验仿真。NSL-KDD数据集有含125 973个训练样本和22 543个测试，有4个攻击类型，提取了41个分类特征，分为符号特征，0-1类型特征和百分比类型特征。UNSW-NB15数据集有175 341个训练数据和82 332个测试数据，包含9个攻击类，提取了44个数据特征，主要分为：时间特征，内容特征，流特征，基本特征，标记特征和其他原始特征。具体的数据特征分布如表1。

表1 NSL-KDD和UNSW-NB15数据集的特征分布Table 1 Feature distribution of NSL-KDD and UNSW-NB15 datasets

为了提高模型的训练效率，在预处理中对特征数据进行归一化处理，将非数值特征数据转换为数值，使所有的特征值处于相同的数量级［16］，并采用10折交叉验证进行数据仿真，取10次交叉仿真结果的均值作为对算法性能的估计。

3.2 检测精度分析

IDS检测数据的准确率是分析算法精度的重要指标，可以评估不同特征选择方法的有效性。在两个不同的数据集中分别选择几组特征子集进行训练，可以提高算法的可靠性和稳定性。MIGM，MDFIFS和CSCA在SVM分类器中的检测准确率结果如图2所示。

根据图2所示，算法的检测准确率随着特征子集的增加而增加，达到稳定值后变化不明显。CSCA检测的准确率明显更高，平均准确率比另外两个算法提高了约5%，达到95.2%。MIGM算法受冗余特征的影响较大，在准确率达到峰值后，检测准确率随着特征的增加有明显下降。但CSCA达到收敛时选择的特征数更少，说明该算法降低了候选特征的冗余性。

图2 不同数据集中算法的检测准确率分析Fig.2 Analysis of detection accuracy of algorithms in different data sets

算法收敛时，IDS的召回率和查准率也能直接反映特征数据选择算法的检测精度。表2和表3记录了不同数据集中算法仿真的平均召回率、查准率和F1值。

在算法的仿真结果中，通过观察不同特征数在多次10折交叉验证中的综合指标的均值，可以对比不同算法检测正常数据的精度。从表2和表3中可以看到CSCA在两个数据集中的检测结果都比较稳定，相比于另外两个算法，该方法R和P的结果表现更好，且综合调整的F1值分别达到0.955和0.950，明显提高了模型的检测性能。

表2 NSL-KDD数据集中算法的平均综合指标分析Table 2 Analysis of the aver age comprehensive index of the algor ithm in the NSL-KDD dataset

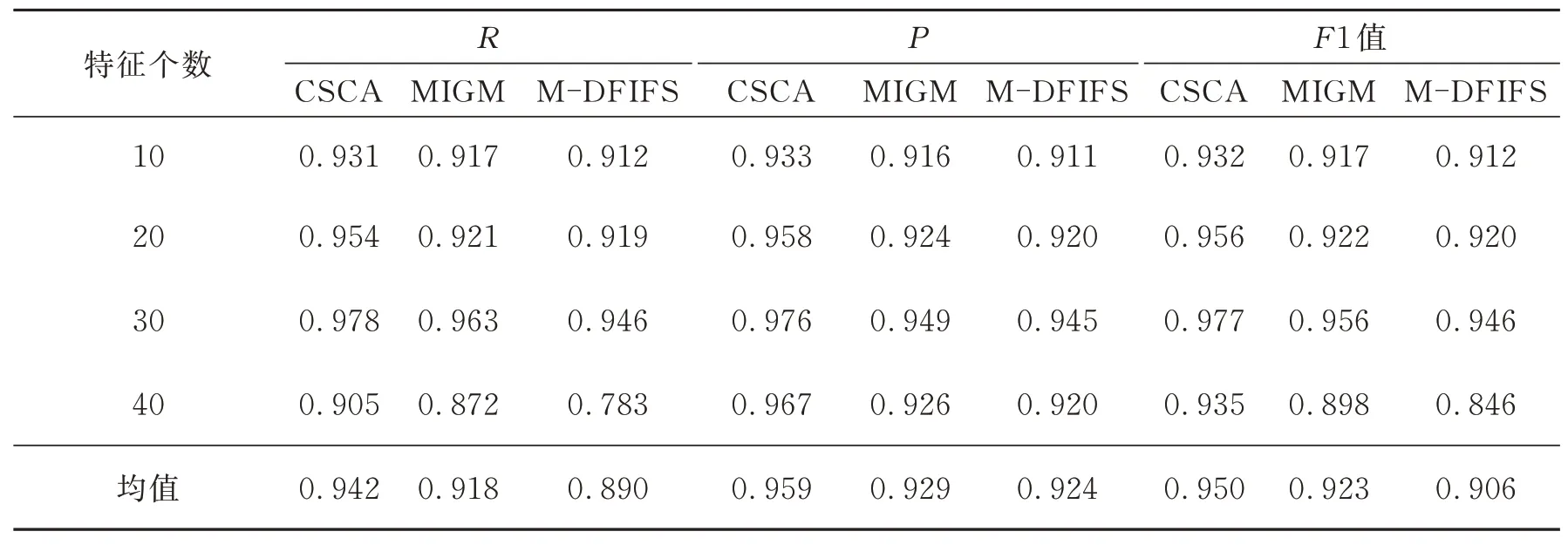
表3 UNSW-NB15数据集中算法的平均综合指标分析Table 3 Analysis of the average comprehensive index of the algorithm in the UNSW-NB15 dataset

3.3 误报率分析

误报率是衡量IDS系统性能的关键指标，误报过高会导致系统检测性能下降。随着特征选择个数的变化，NSL-KDD数据集和UNSWNB15数据集的误报率结果如图3所示。

从图3可以看出，选择的特征过少时，特征子集不足以代表所有的类别信息，算法检测数据的误报率较高。随着特征个数的增多，算法的误报率整体呈下降趋势，但在某些区域会出现增长的情况，这主要是受到冗余特征的影响。CSCA通过偏差校正后减少了冗余特征，模型的平均误报率均比另外两个算法低3%左右，并且收敛性更快，训练选择最优的特征子集后的误报率都接近0.01，可以在数据动态变化时减少分类错误。

图3 不同数据集中算法的误报率Fig.3 False alarm rate of algorithms in different data sets

4 结语

在面临高维复杂的网络入侵数据时，传统MI特征选择算法的性能达不到理想的效果。基于动态离散化的CSCA能更好地减少特征冗余，选择最优的特征子集。利用离散化方法对所有候选特征预处理，再根据MI的特征选择标准计算相关偏差；然后通过卡方检验校正偏差目标函数，最后选出当前最重要的特征子集。仿真结果表明，CSCA精确提取重要的数据特征，使IDS具有更高的检测精度和更低的误报率。为了提高IDS对未知攻击的检测度，下一步将深入研究如何应对数据流中的漂移变化。