基于Prophet模型的湖北省月降水量预测

许浩然，陈中举，杨兆前，房梦婷，詹 炜

（1.长江大学计算机科学学院，湖北荆州434023；2.兰州大学资源环境学院，兰州730000）

0 引言

降水量是反映气象变化的重要指标，也是区域淡水资源的主要来源[1-5]。然而降水往往受气象、地形等多方面复杂因素的影响，且具有不确定性和多变性[6,7]。如何准确的对降水量进行预测，是目前国内外研究的热点。

近年来，众多学者在降水量预测问题上进行了研究，其方法主要分为传统的概率统计法和机器学习算法。在传统的概率统计法上，郝慧慧[8]等人使用灰色波形预测法对河南省的降水量进行预测，刘德林[9]使用ARIMA 模型对郑州市的年降水量进行预测，结果表明该模型在短期降水量预测中效果较好；在机器学习算法上，欧阳琦[7]等人采用支持向量机（SVR）回归的方法对吉林西部降水量进行预测，王宇博[10]等人使用叠加马尔可夫链和BP 神经网络建立降水量预测模型并进行对比分析，结果表明BP 模型在降水量预测中更适用。传统的概率统计法ARIMA、灰色预测模型和机器学习算法SVR、BP 模型(ANN 的一种)已经被广泛用于降水量预测中，并取得较好的效果。

然而ARIMA 模型通常要求稳定的时序数据，且在差分时提取的为固定周期的信息，往往很难符合现实数据的情况；SVR 和BP 模型则存在机器学习算法典型的拟合速度慢、理论可解释性不强的问题。

近年来，深度学习算法Prophet 模型在金融股价预测和电力负荷预测中已经取得了较好的效果，但关于该模型在降水量预测的研究仍然空缺。与上述模型相比，Prophet 模型无需固定周期的时间序列，可以对缺失的数据进行自动拟合，模型的拟合速度快，参数的可解释性强，且对中长期的时序预测能力较强。

在此背景下，本文提出将机器学习算法中的Prophet 模型应用到地学领域中的降水量时序预测上，对湖北省月降水量进行预测。并与现有的降水量预测模型ARIMA、SVR、BP 模型进行对比，以探讨该模型在降水量预测中的可行性，为湖北省气象预测工作提供参考。

1 研究区概况与数据来源

1.1 研究区概况

湖北省位于长江中下游地区，年平均降水量在800-1600 mm 之间。地势大致为东、西、北三面环山，中间低平，略呈向南敞开的不完整盆地，包含了山地、平原和丘陵等多种复杂地形区域[11-14]。降水量在地域分布上呈现自南向北递减的趋势，具有明显的季节性变化，使用传统的模型难以进行准确的预测。本文根据湖北省自然地理和气象特点，参照湖北省气象预报服务分区，将研究区域划分为：鄂西北、鄂西南、江汉平原、鄂东北、鄂东南5个不同区域进行月降水量预测的研究。

1.2 数据来源

本文所使用的数据来源于中国气象数据网(http://data.cma.cn)，选取1960-2017年湖北省月降水量数据构建数据集；根据湖北省气象研究区域划分，每个区域选取3个气象观测站点进行研究，其站点分布情况如图1所示。

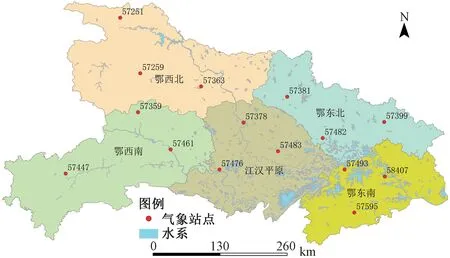
图1 湖北省各区域气象站点分布图Fig.1 Distribution map of meteorological stations in various regions of Hubei Province

2 研究方法

2.1 Prophet模型

Prophet 模型是由Facebook 开源的可分解的时序预测模型[15-17]。与传统的统计学模型相比，Prophet 模型具有灵活性强，可以根据趋势适应不同的季节和时期，对缺失的数据可以进行自动拟合的优势。与常见的机器学习模型相比，Prophet 模型拟合速度快，模型交互式探索性强，且具有很好的理论可解释性。该模型的工作流程如图2所示。

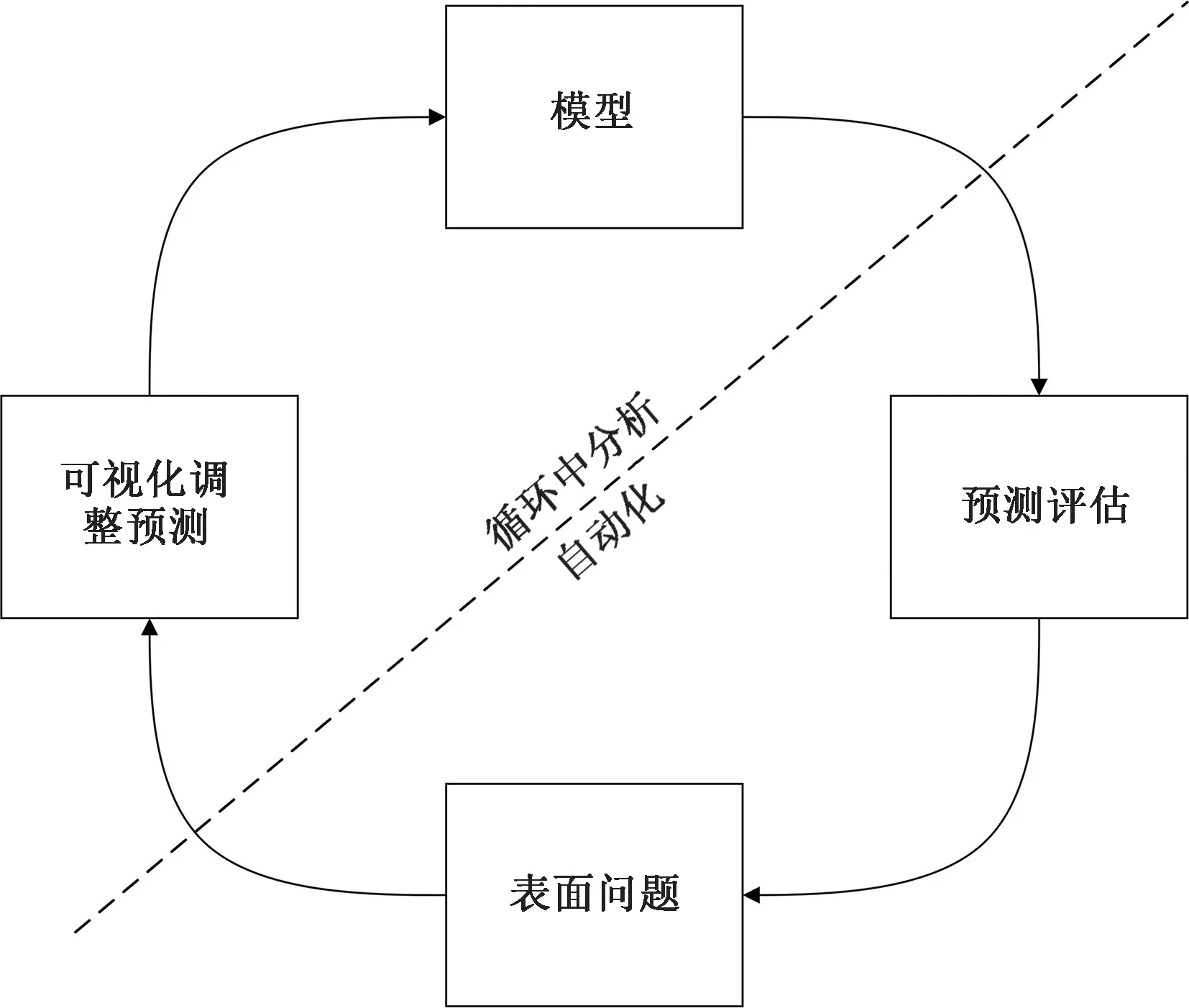
图2 Prophet模型工作流程图Fig.2 Prophet model work flow chart

Prophet 模型主要由四部分组成，其表达方程式如公式（1）所示：

式中：g(t)为趋势函数，主要用于表示时间序列在非周期上的变化趋势；s(t)为周期函数，用于表示时间序列中周期或季节性变化；h(t)为假期函数，用于表示时间序列中节假日所产生的影响，本文将h(t)等效转化为时间序列上的极端天气造成的降水量突变情况，使模型降水量预测更加准确。ϵ(t)为噪声项，代表残差波动，即模型未预测到的趋势。

此外，Prophet 模型还可以将上式中的加法替换为乘法，组成乘法模型。该模型常用于非线性复杂的预测中；由于降水量时序数据为波动的非线性数据，因此本文选取乘法模型。

Prophet模型中的趋势因子g(t)包含两种结构，分别为基于Linear Regression 的分段模型和基于Logistic Regression 的饱和增长模型。分段模型的方程式如公式（2）所示：

式中：k表示模型的增长速率；δ为k的变化量；m为偏移量；t为时间戳；a(t)为指示函数；a(t)T为a(t)的转置向量；γ为平滑处理的偏移量，其作用是使函数分段连续。

Prophet 模型可以通过设置变点，来改变增长率，从而将趋势变化纳入到模型中。假设对于时间戳t，存在n个变点，则a(t)=(a1(t),…,an(t))T，γ=(γ1,…,γn)T；对于某一时刻sj，其偏移量γj，γj= -sj δj，若时间戳t≥sj，则aj(t)= 1，否则为0。

基于Logistic Regression 的饱和增长模型的方程式如公式（3）所示：

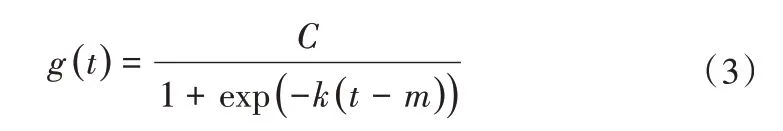
式中：C表示模型的承载力；k，m同上。

由于时间序列上的降水量数据往往存在变点，其承载力并非固定不变的，可通过对模型设置变点来提高模型的预测精度，设置变点后的方程式如公式（4）所示：

Prophet 模型的季节性因子s(t)采用傅里叶级数来建立周期性模型，即如公式（5）所示：

式中：P代表时间序列中的周期，其参数可以表示为β=[a1,b1,…,aN,bN]T，其中，β~Normal(0，σ2)，在Prophet 模型中，σ可以通过seasonality_prior_scale 参数进行设置，从而控制季节因子s(t)对模型的影响大小。

为了降低少数极端天气造成的降水量数据过高对模型普遍降水量预测的影响，本文提出将Prophet 模型的节假日因子h(t)等效转换为极端天气情况。其方程式如公式（6）所示：

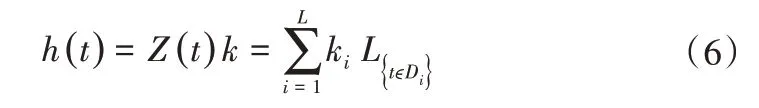
式中：ki表示节假日极端天气的影响范围；Di表示极端天气的前后日期；L为极端天气个数。其中k服从正态分布，即k~Normal(0，v2)，在Prophet 模型中，v可以通过hoildays_prior_scale参数进行设置，从而控制节假日因子对模型的影响大小。

本文基于Prophet 模型建立降水量预测模型，其模型工作原理如图3所示。

图3 Prophet降水量预测模型工作原理Fig.3 The working principle of the Prophet precipitation prediction model

2.2 对比模型

2.2.1 SVR模型

SVR 模型主要用于解决回归问题，其模型的预测精度相比传统统计学模型有所提升，目前在回归估计、水文预测等方面已经取得广泛应用[18]。SVR 模型采用SRM 原理，通过核函数将非线性问题转换为超平面上的线性问题进行求解，大大减小模型的计算量。SVR模型的表达式如公式（7）所示：

式中：α(x)为低维空间到高维的非线性映射；ω为特征向量；b为偏差[19]。

SVR 模型通过结构风险最小化原理，引入松弛因子、拉格朗日乘子以及核函数，将公式（7）转换为公式（8），得到下列最优回归函数：

本文采用的核函数为SVR 最常用的RBF 核函数，将其代入公式（8）得到模型的预测值，其计算如公式（9）所示：

式中：σ为核函数的参数。

2.2.2 BP模型

BP 神经网络是一种较为出色的ANN 模型，广泛应用于水文、气象等领域，如张斌[20]使用BP 模型进行地下水的动态预测。该模型主要由正向和反向两个过程组成。

在正向过程中，输入x依次经过输入层、隐藏层、输出层的处理得到输出值。如果输出值和期望值不同，就进入反向过程。

在反向过程中，将正向过程得到的输出值，经过隐藏层再反向回传，并对各层参数计算的误差求取平均值，最后利用这些平均误差来调整各个参数的权值。

BP 模型可以近似理解为加上了反向传播和反馈的多层感知器。在反向过程中，模型参数总误差的计算如公式（10）所示：

式中：Etotal为总误差；target为模型期望的输出值；output为模型实际的输出值。

2.2.3 ARIMA模型

ARIMA 模型是统计学中常用的模型，广泛应用在水文、股价等时序预测领域。ARIMA 模型可以简单理解为AR 模型、MA 模型和差分法的结合，模型主要分为识别定阶、参数估计、模型校验以及预测4 个阶段。识别定阶用于确定p、d、q3 个参数，其中p代表AR 项，d代表差分的阶数，q代表MA项；参数估计和模型检验主要用来估计未知参数的值以及确定模型是否可靠。

2.3 精度评估方法

本文所采用的模型精度评估方法为均方根误差（RMSE）、平均绝对误差（MAE）。其计算方程式如公式（11）和公式（12）所示：

式中：h为气象站点数；yg和为第g时刻的实际观测值和预测值。

3 结果及分析

3.1 单个站点预测结果及分析

本文基于Prophet 模型建立了湖北省月降水量预测模型，将数据集按照8∶2 的比例划分为训练集和验证集，即使用1960年1月-2006年5月的数据进行模型的训练，2006年6月-2017年12月共139 个月的数据进行验证。通过Prophet 模型进行时序分解，观察趋势项及周期性规律，进而对模型的参数进行调整。实验表明，对于湖北省月降水量预测，Prophet 模型中的乘法模型和基于逻辑回归的饱和增长模型具有较好的预测结果。在模型参数调整中，变点数量n的设置及趋势项灵活度参数changepoint_prior_scale、 周期项灵活度参数seasonality_prior_scale、假期项灵活度参数holidays_prior_scale在较大程度上影响模型的预测效果。由于不同站点间气象规律不同，Prophet 模型可以通过对不同站点进行时序分解，分别调整参数来找到最优模型。

以57259 站点为例，Prophet 模型在验证集上的预测值和真实值如图4所示。从趋势预测上看，通过对比预测数据和实际观测数据发现，Prophet 模型在预测时较好的预测了波峰出现的波动情况，且能够较为准确的对139个月的降水量进行预测，预测结果和实际结果较吻合；SVR 模型可以预测到波峰存在的波动情况，但其预测的峰值往往低于观测值；BP 模型对于趋势波动的预测效果和SVR 类似，但其对波谷的预测往往高于观测值，且对中长期预测能力较弱，后期出现发散现象。ARIMA 模型没有很好的预测到波峰出现的波动情况，其曲线相对波动的观测数据较为平滑，且对中长期预测效果较差，后期出现阶梯性增长和发散现象。

图4 57259站点不同模型降水量预测结果Fig.4 Precipitation results of different models at 57259 site

使用Prophet、SVR、BP 和ARIMA 四种模型对57259 站点预测精度如表1所示，Prophet 模型的RMSE为33.303，MAE为24.060，相比其他模型均为最低，误差相对较小；且预测精度由Prophet 到ARIMA 依次降低，RMSE和MAE较其他模型平均值低18.402和16.189。

表1 57259站点不同模型预测精度评价指标对比Tab.1 Comparison of prediction accuracy evaluation indexes of different models at 57259 site

3.2 不同区域预测结果及分析

为了验证Prophet 模型对不同区域多个站点降水量预测的普适性，本文对湖北省五大区域15 个站点建立Prophet 模型进行降水量预测，并将其与SVR、BP、ARIMA模型进行对比，4个模型的预测精度如图5和图6所示，详细数值见表2。

观察图5、图6 以及表2 发现，从各站点预测效果来看，Prophet 模型对大部分站点的预测效果较好，少数站点的预测效果较差，但该模型对这些站点预测的RMSE和MAE值仍小于其他3种模型，且对总体趋势的预测比较吻合。说明相比于传统模型，Prophet 模型对各区域各个站点的预测精度更高，在湖北省月降水量预测中更具有普适性。

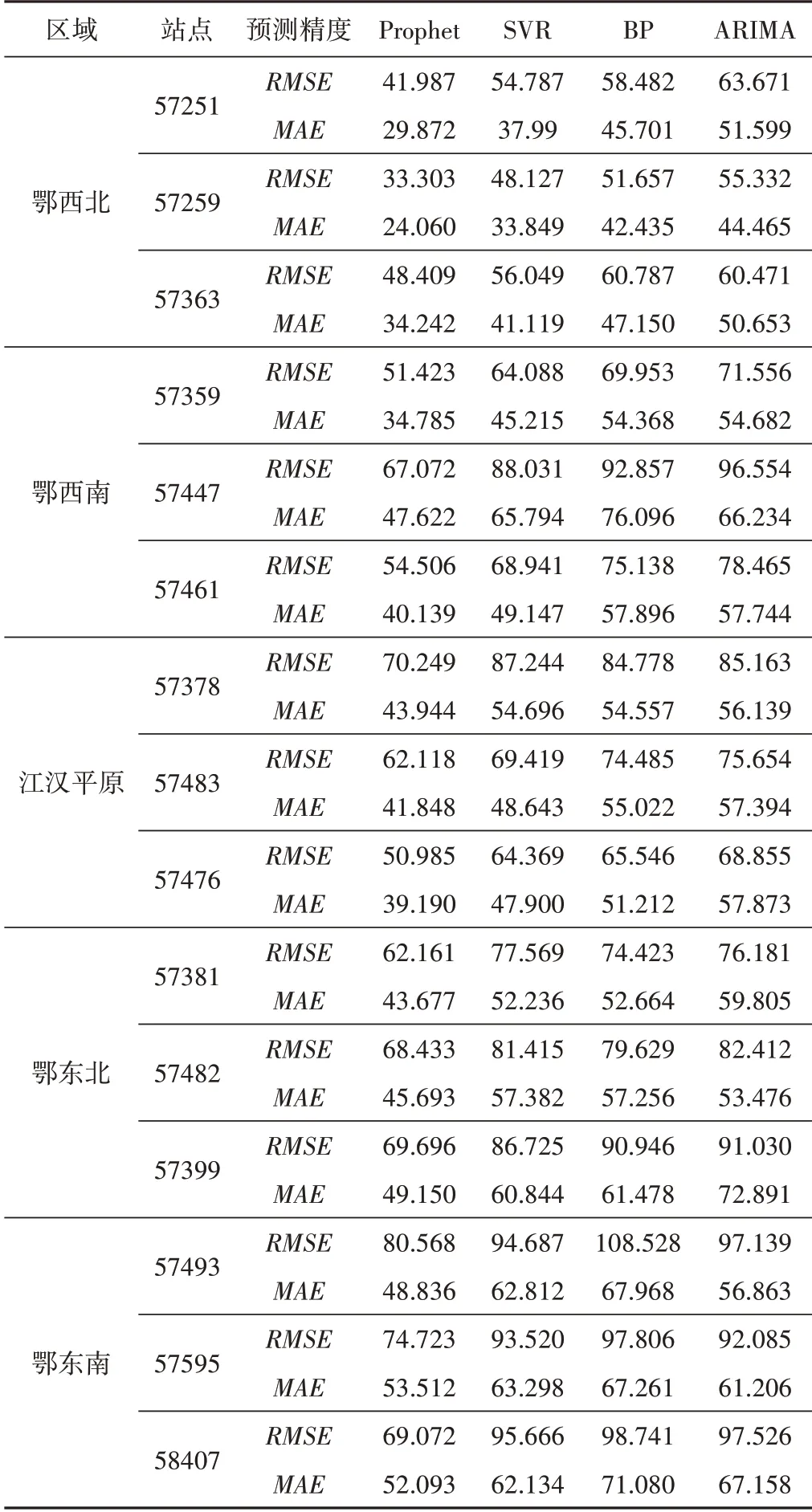
表2 湖北省五大区域15个站点不同模型预测精度评价指标对比mmTab.2 Comparison of prediction accuracy evaluation indicators of different models at 15 stations in five major regions of Hubei Province

图5 湖北省五大区域15个站点RMSE值对比Fig.5 Comparison of RMSE values of 15 stations in the five major regions of Hubei Province

图6 湖北省五大区域15个站点MAE值对比Fig.6 Comparison of the MAE values of 15 stations in the five major regions of Hubei Province

从区域预测效果来看，Prophet 模型对鄂西北区域的预测效果最好，对鄂东南区域的预测效果较差，而Prophet 模型在湖北省鄂西北、鄂西南、江汉平原、鄂东北、鄂东南五大区域的预测精度相比其他模型，RMSE 比其他模型的平均值低了15.363、20.731、13.940、15.496、22.512，说明Prophet 模型虽然对鄂东南区域的预测效果较差，但RMSE减少最多，相比其他传统模型仍具有一定优势。

3.3 降水量预测值空间分析

为了进一步分析Prophet 模型和SVR、BP、ARIMA 模型对湖北省各区域的预测情况，本文利用普通克里金插值法[21-25]对2006年6月-2017年12月共139 个月的月均降水量的真实观测值和各模型的预测值进行空间插值，结果如图7所示。

通过分析图7发现，湖北省降水量总体呈由西北向东南递增的趋势，且随海拔高度减小而增加，形成了以东南区域为中心的降水高值区，以西南区域为中心的次高值区。而通过对比四种模型的降水量预测值和真实观测值的空间插值分布发现，Prophet 模型除西南部57447 站点附近区域的预测效果较差外，其总体趋势变化和等值线变化最为接近；而BP 和SVR 模型虽然总体趋势变化也较为接近，但其在西北和江汉平原区域的预测效果较差，且等值线范围存在较大偏差。此外，通过查看对应站点的历史数据发现，西南部的降水量充沛，出现的突变极大值较多；而Prophet 模型对该区域的降水量趋势预测虽然较为吻合，但其预测的突变极大值低于观测值，因此在进行空间插值取平均值时，该区域的插值的效果较差。

图7 4种模型降水量预测值和实际观测值的空间插值分布Fig.7 The spatial interpolation distribution of the predicted precipitation values and actual observation values of the four models

通过对比4 种模型预测值和真实观测值的等值线变化发现，Prophet 模型的变化趋势和等值线变化范围与真实值等值线变化范围最为接近，都在70~130 的范围之中；而在从各站点所处的等值线范围分析表明，Prophet 除西南部57447 站点、东南部57493站点的少部分区域预测效果较差以外，其他大部分站点的预测效果较好，各站点降水量预测值的空间分布与实际分布结果比较接近。而SVR、BP、ARIMA 模型虽然在总体变化趋势较为吻合，但其具体的等值线数值范围与真实观测值相差较大，且部分站点所处的等值线范围与真实值观测值误差较大，说明Prophet 模型较其他3 种模型在湖北省月降水量中的整体预测效果更好。

4 结论

本文提出将Prophet 模型应用在降水量预测领域，并将其与传统的SVR、BP 和ARIMA 模型进行对比分析，以探讨该模型在降水量时序预测中的可行性。通过使用湖北省1960年1月-2006年5月的月降水量时序数据对模型进行训练，并对2006年6月-2017年12月的月降水量进行预测，实验结论如下：

（1）在单站点的月降水量预测中，Prophet 模型的预测精度要优于传统的SVR、BP 和ARIMA 模型，能够更好的预测到月降水量的周期性以及变化趋势，且对波峰出现的波动情况预测更为准确。

（2）在对湖北省五大区域各站点预测中，Prophet 模型在各站点、各区域的预测效果均优于传统的SVR、BP 和ARIMA模型。其中对鄂西北地区的预测效果最好，鄂东南地区的预测精度相对较差，但仍优于传统的模型，表明该模型在湖北省月降水量预测中具有普适性。

（3）在空间分布上，使用克里金插值法对Prophet、SVR、BP、ARIMA 模型在月均降水量上的预测值与各站点实际观测值进行分析发现，Prophet 模型预测的月降水量在空间上与实际观测值更为吻合，表明该模型在大尺度空间的预测上具有较高准确度。

实验结果证明了Prophet 模型在降水量时序预测上的可行性，且比其他传统模型的预测精度更高。论文将机器学习算法与降水量预测进行结合，为该领域的研究提供了新的思路。