河套灌区畦田内不同位置土壤入渗特性及影响因素分析

孙 娜，李瑞平，苗庆丰，范雷雷，周利颖，李聪聪

（内蒙古农业大学水利与土木建筑工程学院，呼和浩特010018）

0 引言

农田土壤水分入渗过程是影响畦灌性能的重要因素之一，是灌区进行地面灌溉设计的重要基础，同时也是农田水文关系演变、土壤侵蚀和营养物质迁移转化等领域研究的热点[1-3]。由于农田土壤水力特征、土壤结构及人类活动等因素的影响，不同区域位置的差异导致土壤水分入渗过程表现出一定的时空差异性和尺度依赖性，进而给农田畦灌系统的设计带来困难[4,5]。因此，准确认识畦田不同位置土壤水分入渗特性的差异，选取适宜模型进行水分入渗过程模拟，对农田合理灌溉和节水增产具有重要意义。

国内外专家学者基于野外试验、室内模拟试验和模型模拟等手段，开展了大量关于土壤水分入渗过程的研究，并取得丰富的理论成果[6-8]。贾宏伟等[9]利用简化的Phillip 公式和土壤转换函数研究了入渗系数α、稳渗率fc的空间变化规律；聂卫波等[10]将标定理论与地统计学相结合对Phillip 入渗公式进行标定，研究相关标定因子空间变异特征；Rodríguez Vásquez等[11]利用Phillip 和Kostiakov 模型研究入渗参数的空间变异性与土壤容重、土壤密度、沙粒、黏粒和石灰肥料之间的关系；李丽梅等[12]分析指出土壤入渗性能参数中稳渗率和累积入渗量具有强烈的空间变异性；刘继龙等[13]利用多重分析得出稳定入渗率的空间变异性主要受土壤容重、粗粉粒和黏粒含量的影响；何丹等[14]研究指出土壤容重、有机质和初始含水率是影响耕作地入渗过程的主要变异源。

综上所述，土壤水分入渗空间变异性的研究主要集中于基于数理统计研究入渗能力有关指标的差异性，而针对黄河水灌溉含沙量较高和土壤理化性质差异明显的典型区域土壤入渗过程的差异性研究较少。因此，本文选取河套灌区典型试验区，开展畦田土壤水分入渗问题研究，通过对比分析试验区田块内畦首、畦中和畦尾的入渗过程，揭示畦田田块内不同空间位置土壤水分入渗过程、入渗率、累积入渗量和入渗系数的差异性，并运用不同入渗模型对入渗过程进行拟合，选择最适宜试验区畦田灌溉的土壤入渗模型，为深入认识河套灌区畦田土壤水分入渗空间变异状况提供基础资料，为河套灌区农业农田灌溉和耕作提供理论参考。

1 材料与方法

1.1 试验区概况

田间试验区位于气候、土壤和水盐状况较为典型的内蒙古自治区巴彦淖尔市河套灌区双河镇进步村六社酒庄试验站（107°18´23.12″E，40°41´17.24″N），试验区地貌多以平原为主，属中温带大陆性半干旱气候，降雨量少而蒸发较强，年均蒸发量2 032 mm，年均降水量仅为132 mm，降水量季节性差异特征明显且年内分配不均，雨季多集中在7-8月份，占全年降雨量的70%~80%，年平均日照时数为3 180 h，灌水生育期内平均气温为20.9 ℃，无霜期约为126 d。试验区土壤呈微碱性，土壤质地类型分为2 层，上层0~20 cm 为粉土，土壤容重为1.42 g/cm3，田间持水量为22.35%；下层20~40 cm 为黏土，土壤容重为1.39 g/cm3，田间持水量为26.14%；试验区土壤平均储盐量约为1 342 g/m3，为中度含盐土壤。

1.2 试验设计与数据处理

本文研究采用田间试验与室内试验相结合的形式，于2017年4月对试验田地进行激光平地。为避免作物生长、施肥等因素的影响，分别于2017年10月和2018年10月在农作物收割后进行土样采集和入渗试验，并记录采样点周边环境信息。综合考虑试验区地形和植被种植情况，选取长宽为45 m×21 m 的畦田田块，将田块按水流推进方向分为畦首、畦中、畦尾，并按图1所示布置入渗试验点。参照图1 中网格交点的位置，每个样点重复取样3次，使其具有代表性，能反映整块畦田的土壤理化性质分布格局。

图1 试验布置(单位：m)Fig.1 Test layout

土壤入渗过程采用双环入渗仪进行测定，双环入渗仪内环和外环直径分别为26 cm 和60 cm，内、外环高度均为25 cm。田间试验时，首先清除表层土壤，将内、外环埋入地面以下深度20 cm 处，然后关闭所有阀门，连接管线并给内环供水，用马氏瓶计量。入渗试验采用当地黄河水，测定含沙量为3%，试验过程中水深控制在2 cm，内外环水位齐平，外环水位采用水位平衡装置控制，确保内环属于一维垂直入渗条件，减少积水水头对水势梯度的影响[15]。入渗水量分不同时段记录，在试验的0～15 min 每隔30 s 记录一次；15～30 min 每隔1 min 记录一次；30～60 min 每隔2 min 记录一次；60～90 min每隔5 min记录一次，90～120 min每隔10 min记录一次。

土壤理化性质测定指标主要包括土壤质地、土壤含水率、土壤含盐量和土壤容重等。土壤含水率采用土钻取土烘干法测定，土壤容重采用环刀法测量，土壤pH 和电导率（EC）按照水土比为5∶1 来配置样品液，搅拌静置后测定[16]；土壤样品的机械组成采用MS 2000 型激光粒度仪测定，并按照国际制土壤粒径分类标准把各粒级组含量定义成黏粒（＜0.002 mm）、粉粒（0.002～0.02 mm）和砂粒（0.02～2 mm）[17]。

本文采用GS+9.0 对土壤基本理化性质的空间分布格局进行研究分析其差异性特征；利用Orgin 2019软件对土壤入渗过程进行模型拟合及绘图，选择适宜本研究区的最优入渗模型；采用SPSS 19.0 软件分析入渗率与影响因素之间的相关性，探究土壤入渗空间变异性的原因。

1.3 研究方法

描述土壤水分入渗特征的指标有初始入渗率、稳定入渗率、90 min累积入渗量和入渗系数，土壤初始入渗率反映入渗初期单位时间内地表单位面积土壤的入渗水量，稳定入渗率反映入渗后期水流较为稳定时的入渗速率，它等于或接近于饱和导水率，而土壤的入渗过程一般可在90 min 内达到相对稳定程度，因此，本文选取90 min 的累积入渗量作为反映土壤入渗能力的指标[18,19]。分别采用具有代表性的Kostiakov 模型、Philip 模型、Horton 模型及通用经验模型对土壤入渗过程进行拟合分析[20]。

Kostiakov模型：

式中：I（t）为入渗速率，mm/min；t为入渗历时，min；K、α为经验系数；f0为初始入渗率，mm/min。

Philip模型：

式中：f（t）为入渗速率，mm/min；t为入渗时间，min；S为土壤吸湿率，mm/min0.5；A为稳定入渗率，mm/min。

Horton模型：

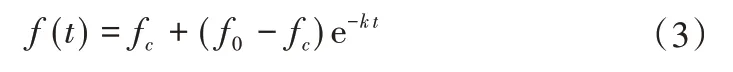
式中：f（t）为入渗速率，mm/min；t为入渗时间，min；f0为初始入渗率，mm/min；fc为稳渗率，mm/min；k为模型参数，参数k决定f从f0减小到fc的速度。

通用经验模型：

式中：f（t）为入渗速率，mm/min；t为入渗时间，min；a、b为拟合的模型参数；n为经验系数。

2 结果与分析

2.1 土壤理化性质特征分析

为了分析试验区内土壤理化性质，直观了解畦田内土壤理化特性的空间分布状况，现根据最优半方差函数模型，选择Kriging 插值法，利用GS+9.0 绘制了0~40 cm 耕作层土壤理化特性空间分布的平面等值线图，如图2所示。从图2 可知，在整个试验田块范围内，土壤含水率呈现由田块中心向四周逐渐增大的变化趋势，含水率的变化范围为10.98%~21.21%，含水率呈畦首＞畦尾＞畦中的分布特征，且含水率等值线图比较密集，说明不同位置间含水率差异较明显；试验田块内土壤容重的变化范围为1.50~1.63 g/cm3，呈条状分布且空间范围内差异性较小，受大型机械压实作用影响，土壤容重主要在畦首区域出现高值，而畦尾的土壤质地疏松多孔，土壤容重主要出现低值；试验田块内土壤pH 值为7.55~8.15，呈弱碱性，pH 高值区出现在试验田块中部区域，并向畦首和畦尾两侧依次呈现“高-低”交替的带状分布特征，空间分布差异性较明显；试验田块内土壤电导率呈斑块状分布，空间差异性较小，田块内3 个高值区其值分别为0.580、0.577 和0.478 mS/cm，并且分布于畦田两侧。土壤理化性质特征受土壤质地的分布状况影响，试验田块内土壤黏粒含量空间分布过渡比较平缓，土壤粉粒含量在畦中位置较高，土壤沙粒含量在畦首稍高，加之施肥、灌溉、翻耕等人为因素的影响，使得土壤理化性质在空间分布上具有一定的差异性。

图2 0~40 cm耕层土壤理化性质等值线图Fig.2 0~40 cm cultivated layer soil physical and chemical properties contour map

2.2 土壤入渗过程特征分析

为了分析试验田块内土壤入渗过程的变化特征，分别绘制不用空间位置下土壤累积入渗量和入渗率曲线如图3所示。从图3可知，试验田块内土壤累积入渗量和入渗速率随时间的变化过程明显并且在田块内不同位置呈现一定特征。畦首、畦中和畦尾的土壤水分入渗随时间的变化过程基本一致，累积入渗量随着入渗时间的推移不断增大，而入渗率随时间的增加而减小；土壤入渗初期入渗率较大，随后快速衰减并趋于一个相对稳定的入渗率，衰减速度呈逐渐减小的变化特征。累积入渗量呈现畦首＞畦中＞畦尾的变化特征，入渗率则呈畦首＞畦尾＞畦中的变化特征，且在入渗开始后，畦首的初始入渗率下降速度较快，约为畦尾初始入渗率下降速度的2倍；畦首的土壤入渗率达到相对稳定所需的时间远小于畦中和畦尾，在入渗开始55 min 后，畦中和畦尾的入渗率基本趋于稳定，而畦首的土壤入渗率仍在不断变化，直到78 min趋于稳定。

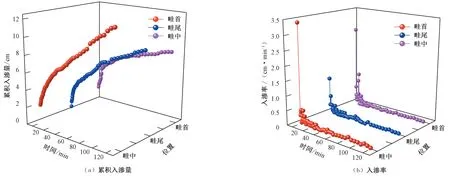
图3 不同空间位置的土壤入渗变化过程Fig.3 Change process of soil infiltration in different spatial positions

现对比试验田块内畦首、畦中和畦尾不同位置土壤入渗特性参数，结果如表1所示。由表1 可知，初始入渗速率、90 min 累积入渗量、入渗系数和稳定入渗率均为畦首最大，畦首的初始入渗率分别是畦中和畦尾的1.42 和1.81 倍，入渗系数和稳定入渗率呈现畦首＞畦尾＞畦中的变化特征，累积入渗量与初始入渗率呈现畦首＞畦中＞畦尾的变化特征。经方差分析显示，畦首的初始入渗率、稳定入渗率和入渗系数均与畦中和畦尾具有明显差异性（P＜0.05），而畦中与畦尾之间的初始入渗率、稳定入渗率和入渗系数无明显差异性。

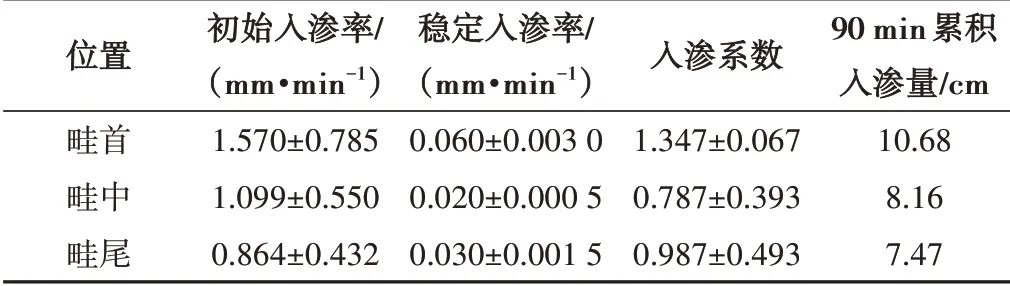
表1 不同位置土壤入渗特性参数Tab.1 Soil infiltration parameters at different locations

2.3 土壤入渗过程模型拟合

土壤水分入渗是一个复杂的过程，国内外众多专家学者建立了多种入渗模型来模拟入渗速率随时间变化的过程。具体依据模型是否具有物理意义划分为2 类：一类是物理模型，主要包括Horton 模型和Philip 模型；另一类是经验模型，主要包括Kostiakov－liews 模型和通用经验模型[21]。本文为进一步研究试验田块内不同位置土壤水分入渗过程，选用以上4个模型对畦首、畦中和畦尾的土壤入渗过程进行模拟，模拟结果如表2和图4所示。

表2 土壤入渗模型拟合参数结果Tab.2 Parameter fit results of soil infiltration model

从表2 和图4 可知，4 个模型拟合度存在一定差异，但决定系数R2均在0.9 以上，说明拟合效果较好，综合考虑4 个模型的决定系数R2，并将模拟参数与实测数据对比分析可知，Horton 模型的R2为0.988～0.997，较其他3 个模型高，且参数反映的结果与实测值的偏差较小，表明Horton 模型更适宜于描述本试验区田块内土壤入渗速率随时间变化的过程。在Horton 模型中，初始入渗速率f0与实测值偏差较小，稳定入渗率fc呈现为畦首＞畦尾＞畦中的变化特征，与试验实测结果一致；经验常数k决定着土壤水分入渗过程中达到稳渗速率的快慢程度，k值越大则越快达到稳定入渗速率，从拟合结果看出，畦尾最先达到稳渗状态，畦中次之，畦首最慢，与实测结果一致。

图4 土壤入渗模型拟合曲线Fig.4 Fit diagram of soil infiltration model

2.4 土壤入渗空间变异性影响因素分析

为探究影响土壤入渗特性空间变异性的因素，现对反映土壤入渗特性的参数初始入渗率、稳定入渗率和累积入渗量与土壤理化性质指标进行相关性分析，结果如表3所示。由表3 可知，畦田土壤入渗特性与土壤理化性质之间具有一定联系。畦首、畦中和畦尾不同位置与土壤理化性质之间相关性具有一定差异，其中土壤容重和含水率与不同位置土壤的入渗特性之间具有较高的相关性，说明土壤入渗过程明显受到土壤容重和含水率的影响，土壤质地和结构发生变化，土壤质地由重变轻，其入渗能力则逐渐增大[22]。初始入渗率在畦首位置与沙粒具有极显著关系，主要由于畦首表层土壤含沙量较大，孔隙大，保水性能较差，导致其渗透速率较快；累积入渗量与畦尾的黏粒含量具有极显著相关，黏粒含量越高，土壤孔隙较小，土壤通气透水性能受到限制，从而导致入渗能力下降，累积入渗量越小；稳定入渗率在畦中与土壤电导率呈极显著负相关，随电导率增加而减小，说明电导率高的土壤盐分含量相对较多，而盐分对土壤入渗特性具有一定的阻碍作用[23,24]。

表3 入渗特性参数与土壤特性相关关系Tab.3 Correlation between infiltration parameters and soil properties

3 结论

（1）试验区田块内不同位置土壤理化性质具有一定差异性，含水率呈畦首＞畦尾＞畦中的分布特征；土壤呈弱碱性，pH 在畦中较高且向畦首和畦尾两侧依次呈现“高-低”交替的带状分布特征；土壤电导率呈斑块状分布且空间差异性较小；土壤容重呈条状分布且空间范围内差异性较小。试验田块内不同位置土壤入渗特性与土壤理化性质之间具有一定联系，土壤容重和含水率对不同位置土壤的入渗特性影响明显。

（2）试验田块内不同位置土壤入渗特性具有一定差异性，畦首位置的初始入渗速率、90 min累积入渗量、入渗系数和稳定入渗率最大，且初始入渗率分别是畦中和畦尾的1.42和1.81倍，入渗系数和稳定入渗率呈现畦首＞畦尾＞畦中的变化特征，累积入渗量与初始入渗率呈现畦首＞畦中＞畦尾的变化特征。

（3）通过选用4个模型对试验田块内不同位置土壤入渗过程进行模拟可知，4个模型拟合度存在一定差异，但决定系数R2均在0.9 以上，拟合效果较好，其中Horton 模型模拟参数反映的结果与实测值的偏差较小，更适宜于描述本试验区田块内土壤的入渗过程。