考虑多工况的起落架结构拓扑优化设计
谢欣宏 张秋生




摘 要:飞机起落架结构在着陆、地面操纵多工况下承担复杂载荷,因此保证起落架结构的承载能力的同时满足轻量化设计,是起落架设计的重点。该文以起落架外筒为例,考虑起落架在使用过程中的若干严苛工况载荷,基于有限元方法,以应力和体积为主要约束,以加权应变能最小化为优化目标,采用各向同性材料惩罚模型进行拓扑优化求解,得到高度适配于使用工况的“强、坚、轻”的结构,基于多工况载荷的优化后起落架外筒质量降低了19.87%。
关键词:起落架 拓扑优化 有限元 多工况 变密度法
中图分类号: V226 文献标识码:A 文章编号:1672-3791(2022)01(b)-0000-00
Topology Optimization Design of Landing Gear Structure Considering Multiple Working Conditions
XIE Xinhong1 ZHANG Qiusheng2
(1.Department of Aircraft, Chinese Flight Test Establishment, Xi’an, Shaanxi Province, 710089 China; 2.Uint 92635, Qingdao, Shandong Province, 210041 China)
Abstract: The landing gear structure of the aircraft bears complex loads under multiple conditions of landing and ground control. Therefore, it is the key point of landing gear design to ensure the carrying capacity of landing gear structure and meet the lightweight design.Taking the outer cylinder of the landing gear as an example, considering several severe working conditions of the landing gear in use, based on the finite element method, taking the stress and volume as the main constraints and the minimization of weighted strain energy as the optimization objective, the topology optimization solution is carried out by using the isotropic material penalty model, and the "strong, hard and light" structure highly suitable for the working conditions is obtained, after the optimization based on multi condition load, the mass of landing gear outer barrel is reduced by 19.87%.
Key Words: Landing gear; Topology optimization; Finite element; Multiple working conditions; Variable density method
起落架是飛机的主要承载部件,其使用过程中涉及三点着陆、两点着陆、对称刹车、操作转弯等多种工况,受载情况复杂[1]。因此,在设计过程中需要着重考虑两方面因素:一是结构传力路径的设计;二是结构的刚度及所用材料的强度特性。随着飞行器的发展,设计和研究人员依据布置形式、构型和任务需求对起落架以及其强度的研究也更加深入[2]。
结构优化的核心在于优化材料的空间分布,在保证结构功能可靠性的前提下最大化材料的利用率。在工程应用中,通常可以采用拓扑优化[3]、尺寸优化[4]和形状优化[5]来对结构进行优化设计。其中,拓扑优化[6]主要用于结构的概念设计阶段或结构的大幅调整改进工作中,可以针对性地根据结构受载情况,优化材料分布形式,求解出最佳的传力路径,能较大程度提高结构性能。
在飞机结构优化设计领域,国内外学者也开展了研究,Chen[7]等人基于应变疲劳分析,对舰载无人机牵引杆疲劳薄弱区进行了优化,Meng[8]等人采用代理模型解决了涡轮叶片设计问题。Munk[9]等人将拓扑优化应用于航空航天设计问题,设计了一种轻型飞机起落架。
国内外学者在不同的飞机结构上进行了尺寸参数和结构优化,但是在考虑多工况下结构复杂受载的条件下,对多特征、多参数结构进行优化,并且不影响原始结构和整机的空间适配性,国内外学者还没有比较系统和完善的解决方案。该文针对某型起落架,考虑其真实使用环境下的若干严苛工况,采用变密度法中的各项同性材料惩罚模型(SIMP)进行拓扑优化求解,在确保结构最大应力值小于材料抗拉强度,优化后结构重量减少这两大前提下,得到传力路径更优、材料利用率更高的结构,高度适配于结构的复杂载荷环境。
1 多工况拓扑优化数学模型
1.1 变密度法的各向同性材料惩罚模型
通常使用材料插值模型对连续体进行拓扑优化,常见的插值方法有均匀化方法、变厚度法和变密度法。其中,各向同性材料惩罚模型(SIMP)和材料属性的合理近似模型(RAMP)是变密度法常用的两种插值模型。
该文采用了各向同材料惩罚模型,其基本原理是通过有限元方法进行结构离散,借助密度插值函数表征元件的相对密度和材料的弹性模量之间的关系,进而影响结构的整体刚度矩阵,并优化材料分布。
SMIP插值模型可以表示为:
E^p (x_i^' )=E^min+x_i^'p (E^0-E^min) (1)
令∆E=E^0-E^min,则上式可以表示为:
E^p (x_i^' )=E^min+x_i^'p ∆E (2)
式中,E^p为插值后的弹性模量,E^0为实体区域的弹性模量、E^min为孔洞区域的弹性模量。实体区域相对密度x_i^'取值范围通常在0~1之间,表示材料从可以去除到需要保留,通过x_i^'的取值来让材料分布最优。模型中还通过引入了惩罚因子P(通常取值为2[10])来对x_i^'取值在中间范围的材料进行修正使其向两极逼近。
1.2 多工况拓扑优化模型及收敛准则
飞机结構优化设计追求“强、坚、轻”,顾名思义,最终目标是在满足结构“强”度、结构 “刚”度的基础上实现 “轻”量化。对应的在设计中需要使用应力约束、柔度约束以及体积分数约束。
该文在考虑多静态工况下,以加权应变能为表征参数,建立了结构拓扑优化模型。式3对优化模型进行了参数化表述。
minC(x^' )={∑_(k=1)^m▒w_k^p [(C_k (x^' )-C_k^min)/(C_k^max-C_k^min )]^p }^(1/p) (3)
s.t. ∑_(k-1)^m▒〖(∑_(j=1)^n▒〖V_j x_j^'k 〗)-V ̅ 〗⩽0
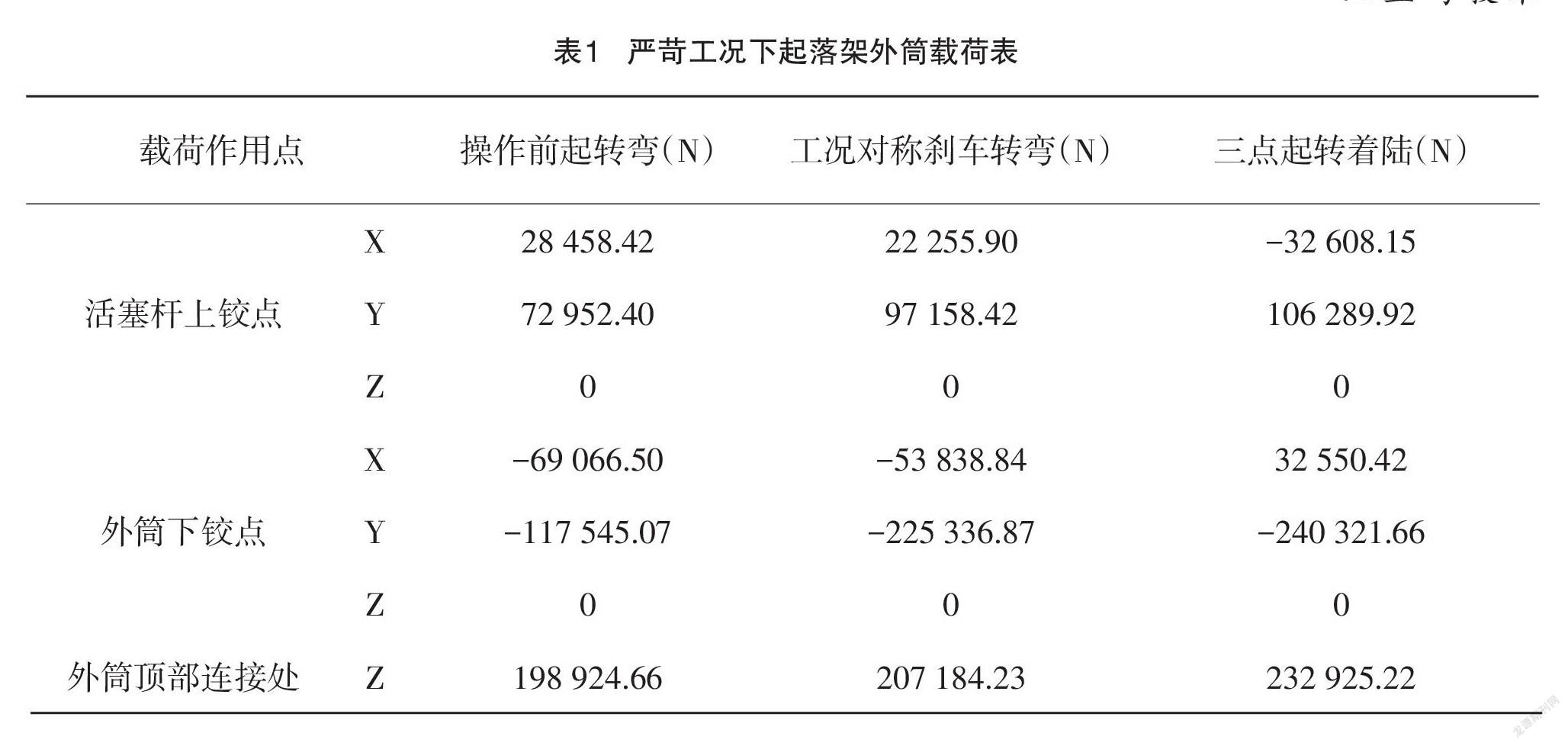
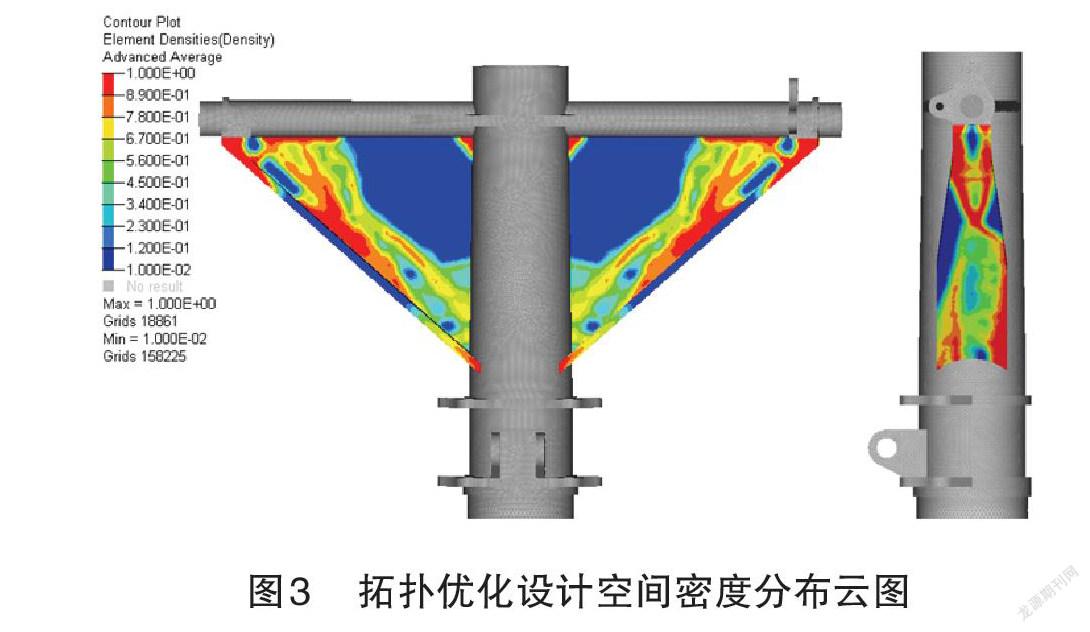
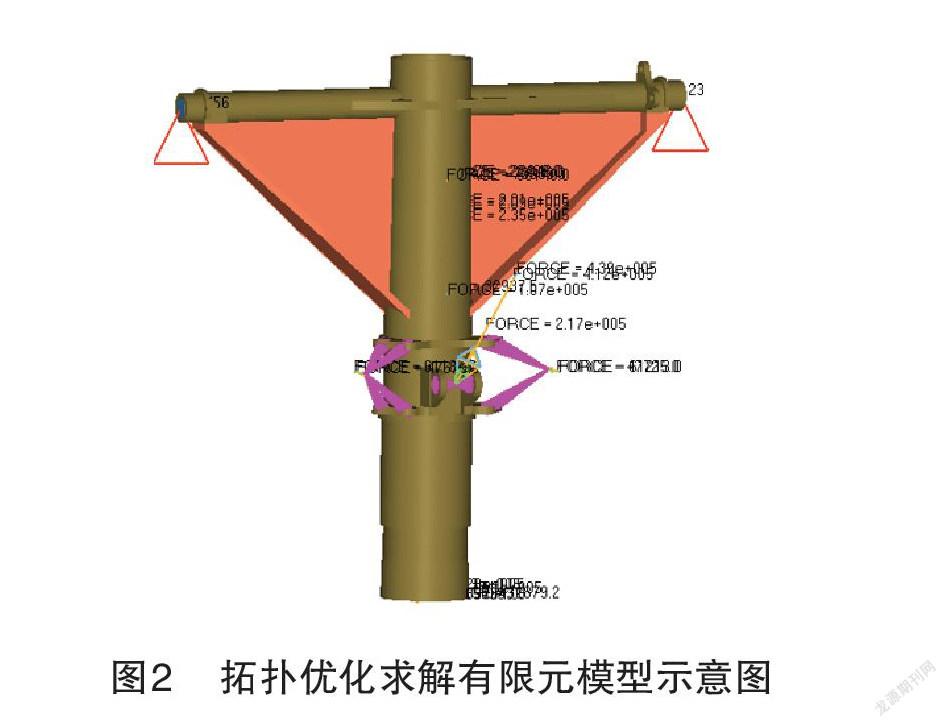
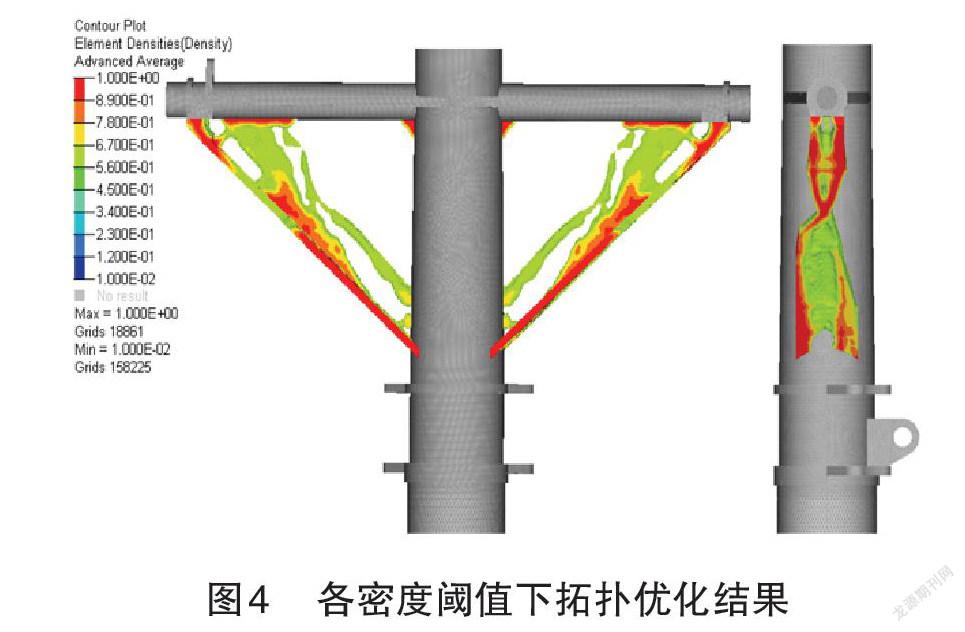
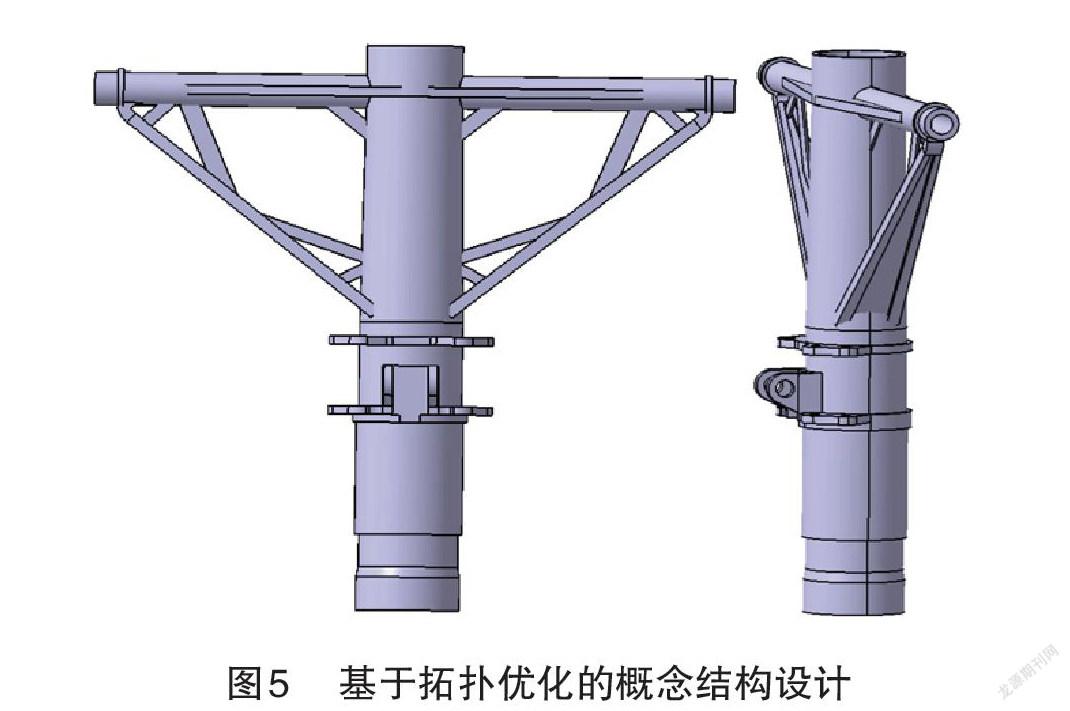
0 j=1,…,n k=1,…,n 式中, C(x^' )为总加权应变能,x^'为相对密度, 为惩罚因子, C_k (x^' )为第k个工况的结构柔度函数,w_k为第k个工况的权值,C_k^max、C_k^max为k工况柔度的最大、最小值,V_j为第j个单元的体积,V ̅为设计空间体积。表示在拓扑求解过程中,在不大于原有设计空间的范围内,各单元的相对密度在0到1之间变化,使得考虑多工况的结构加权应变能最小化。 在满足点距准则、函数下降量准则中的任意准则下,优化问题可以中止计算。 (1)点距准则,两个相邻迭代点D_k、D_(k+1)之间的距离变化足够小或保持不变时,判定优D_(k+1)化求解收敛。 ‖D_k-D_(k+1) ‖⩽ε_1 (4) (2)函数下降量准则,当两个相邻迭代点的目标函数值满足公差标准时,判定优化求解收敛。 |f(D_(k+1) )-f(D_k)|⩽ε_2 (5) 2 起落架外筒结构拓扑优化设计 2.1 优化对象严苛工况载荷提取 经前期有限元计算表明,该型起落架在操作前起转弯、三点起转着陆、对称刹车转弯3种工况下,起落架应力水平较高,3个工况对应的起落架机体最大应力值分别为1 514 MPa、1 446 MPa、1 586 MPa,接近于该型起落架所用高强度钢30CrMnSiNi2A的抗拉强度1 605 MPa。 图1为起落架外筒原始结构示意图。取使用载荷1.5倍为设计载荷,以此作为输入,在LMS Virtual.lab motion是多体系统动力学仿真虚拟实验室中建立起落架的多体动力学模型,求得作用在该文优化对象起落架外筒上的载荷如表1所示。 2.2 优化问题定义与求解 2.2.1建立有限元模型 该文提出的结构拓扑优化方法使用有限元前处理软件Hypermesh进行结构离散,结合Optistruct优化软件进行拓扑优化求解。根据几何清理、网格划分、材料属性赋予、约束等步骤建立起落架外筒有限元模型,取输入的设计载荷进行加载,外筒拓扑优化求解的有限元模型如图2所示。 2.2.2定义拓扑优化的设计空间 为保证优化后结构不影响原起落架的收放空间,设计空间的选择和划分仅限于原结构范围内,为获取更优的传力路径,遂对斜撑杆内部空间进行填充,对优化空间和非优化空间采取赋予不同单元属性的方式来区分。 2.2.3定义响应 该文建立了应力、体积分数和加权应变能3个响应,其中,以加权应变能最小为目标响应,以应力、体积分数和工艺限制为约束响应。同样的,对于设计空间和非设计空间需要分别定义不同的应力响应。 2.2.4优化约束定义 根据上述讨论,该文定义了应力约束、体积分数约束、工艺约束(最小、最大成员尺寸、拔模约束、对称约束等)。该文取1 400 MPa为应力约束上限。设置体积分数上限为0.64,以获得更优的材料分布和传力路径。最小、最大成员尺寸约束可以确保结构可以有更优的传力路径和材料分布。拔模约束和对称约束可提升优化后结构的可加工性。 2.2.5定义优化目标提交求解 优化目标定义为加权应变能最小化,并提交Optistruct解算器进行迭代计算。经过124轮迭代计算,计算趋于收敛。 拓扑优化后,移除了在承载和传力过程中作用较小的部分,优化空间的体积也发生了变化,最终体积分数收敛到约0.5,以满足约束条件。 3 拓扑优化设计拓扑优化结果分析 3.1 空间密度云图分析 拓扑优化的密度分布云图中不同颜色代表着该处材料可以被去除的程度,如图4所示,密度小于0.12的部分为深蓝色,密度大于0.89的部分为深红色,分别表示必须要去除和保留的材料。密度处于两者之间的部分可以结合应力分布以及工艺等因素加以考量进而确定最终的结构。 图4给出了密度阈值为0.55时外筒拓扑优化的结构形式。可以看出,在增加密度阈值的过程中,外筒斜撑的主承载力路径越来越清晰。 在起落架的外筒结构中,筒体与横梁的连接部位、外筒撑杆的底部以及筒体与外筒撑杆顶部与横梁的连接部位由于载荷传递容易产生较大变形,因此需要加强设计。如图5所示,经过拓扑优化后,结构为三角形支撑结构,可帮助外筒承受横向荷载。同时,随着密度阈值的增加,斜撑的中部材料逐渐减少,可以采用两侧厚而中间薄的变厚度设计。 3.2 基于拓扑优化结果的重新设计和验证 上文对外筒结构的拓扑优化可以指导外筒的概念设计, 可以看出,优化设计思路包括采用三角形结构进行加固设计,并通过在两侧加强大厚度钢筋的设计,以及在中间设计较薄的变厚度设计。进而重新设计了如图5所示的新型起落架外筒结构。 该结构优化了起落架外筒的传力承载形式,局部加强设计规避了应力集中的风险,斜撑杆的变厚度设计理念为结构轻量化设计提供了一种可行途径。 进一步地,为了验证优化结果的可靠性,取三点起转工况,将优化后的结果通过有限元方法分析结构强度,优化前后的结果对比如表2所示。 从表2可以看出,优化后的外筒最大应力值为1203 MPa,并未超过材料的强度极限。经过优化过后的外筒,在结构应力值仅仅提升了4.61%的基础上,质量减轻了19.87%。 4 结论 该文以起落架外筒为例,考虑多工况,采用变密度法进行拓扑优化求解,获得如下结果。 (1)在应力、体积分数及相关工艺约束条件下,以加权应变能最小为目标,经过124輪的迭代,计算收敛,最终体积分数收敛到0.55。 (2)结构变化主要体现在两个方面。一是采用三角形结构加强外筒支撑与筒体、梁之间的空间设计;二是对撑杆的两侧厚度加强,中部变薄,采用变厚度设计。 (3)经过优化设计后的结构,最大应力值仅增加了4.61%,但结构质量减轻了19.87%,结果表明该文的方法具有可行性和可靠性。 参 考 文 献 [1] 闫楚良.飞机起落架安全寿命与损伤容限设计[M]. 北京:航空工业出版社,2011:9. [2] 贾玉红,郭可谦.飞机起落架的发展[J]. 机械技术史, 1998(00):425-429. [3] 高文俊,吕西林.拓扑优化在结构工程中的应用[J].结构工程师,2020,36(6):232-241. [4] 石磊,常啸.基于拓扑与尺寸优化的某型飞机起落架扭力臂轻量化设计[J].机电工程技术,2021,50(2):70-75. [5] 吴志学.基于整体-局部技术的结构形状优化策略[J].计算力学学报,2021,38(5):573-579. [6] 杨高宏.基于有限元的车架动态特征拓扑优化仿真分析[J].内燃机与配件,2021(5):48-50. [7] CHEN H,FANG X,ZHANG Z,et al.Parameter Optimisation of a Carrier-Based UAV Drawbar Based on Strain Fatigue Analysis[J].The Aeronautical Journal,2021,125(1288):1083-1102. [8] MENG, D.,YANG, S.,ZHANG,Y,et al.Structural reliability analysis and uncertainties- based collaborative design and optimization of turbine blades using surrogate model[J].Fatigue & Fracture Eng. Mater. Struct.,2019,42(6):1219–1227. [9] MUNK, D.J., AULD, D.J. On the benefits of applying topology opti- mization to structural design of aircraft components[J].Struct Multidiscipl Optim,2019,60(3):1245–1266. [10] 王钰栋,金磊,洪清泉.HyperMesh & MyperView 应用技巧与高级实例[M].北京:机械工业出版社,2012.

