一种二次雷达大气折射距离误差修正方法*

张 银1，王 强1，喻 波2，袁永亭

(1.四川九洲空管科技有限责任公司，四川 绵阳 621000；2.中国西南电子技术研究所，成都 610036；3.中国人民解放军31435部队，沈阳 110015)

0 引 言

二次雷达(Secondary Surveillance Radar，SSR)是一种空管雷达信标系统，是提供空中飞行情报及态势的主要信息来源，不仅是现代空管系统必配设备之一，还广泛应用于军事领域。随着空中交通密度的日益增加，二次雷达分辨目标的能力也越来越受到重视，其距离探测、方位探测的精确性关系到解析交会目标的准确性，因此，提高探测精度是提高飞行密度的有力保障[1-3]。

二次雷达系统采用协同方式工作，系统包括具有询问功能的询问机和应答功能的应答机，通过“一问一答”的方式来获取目标的3/A代码(身份)、C模式高度(气压高度)等信息，同时通过测量应答回波在询问波束内的位置来测量其方位，测量询问信号和应答信号之间的延时来测量距离[2]。

带来二次雷达测距误差的主要因素有机载应答机延时抖动、大气折射、接收系统热噪声、应答处理器时钟采样频率、视频采样误差等[4]。机载应答机延时抖动引起的测距误差可按固定误差进行修正，因为二次雷达检飞是用同一架飞机，这样引入的应答机延时抖动是固定的；接收系统热噪声是一个雷达系统本身固有的特性，其引起的测距误差无法消除；应答处理器时钟采样频率、视频采样引起的测距误差可通过提高采样时钟来减小测距误差，采样时钟也是一个雷达系统在设计时就确定的因素，在设计之初就要选择合适的采样时钟来确保较高的测距精度。目前，大多数二次雷达系统在测距时没有进行大气折射修正，在计算距离时电磁波速度按真空中的速度或固定的修正后的速度来计算，这样会引入大气折射误差，或只兼顾了某一高度层的折射误差，而在其他高度层检飞时测距依然超差。文献[4]在指数模型的基础上根据多次检飞数据得到折射误差修正曲线来修正距离误差，进一步提高了测距精度，但该文献没有提出具体的二次雷达折射距离误差修正模型。为此，本文根据大气折射模型结合某型二次雷达检飞试验数据，提出了一种二次雷达大气折射距离误差修正模型。

1 二次雷达测距原理

二次雷达与一次雷达一样，利用电磁波在空间以光速直线传播的特性来测量距离。询问机在确认检测到应答信号以后，测出接收到应答脉冲相对于询问脉冲的间隔时间，减去应答机响应时间(根据ICAO规定，应答机应在正确接收到询问信号后发射对应的应答信号，响应时间为3±0.5 μs)，即为电磁波往返雷达与飞机之间所用时间，因此，二次雷达的距离测量公式为[5]

R=0.15tr。

(1)

式中：R为飞机到雷达之间的斜距(单位：km)，tr为电磁波往返雷达与飞机之间所用时间(单位：μs)[5]。

2 二次雷达在大气中的折射传播

2.1 电磁波在大气传播中的折射特性

地球大气层是由许多气体和液体以及固体悬浮粒子组成的一个集合。电磁波在穿越大气层时，由于地球表层大气密度分布不均匀，使得电磁波在传播过程中发生弯曲，出现折射现象。折射量的度量是折射指数n，它定义为真空中的传播速度c与媒质中速度v的比值[6]，即

(2)

为研究方便，一般习惯引入物理量N，称为折射率。在微波频段及以下，对含有水汽的空气，折射指数n和折射率N之间的关系为[6]

(3)

式中：es是水汽的局部压力(单位：mbar)，p是大气层的大气压力(单位：mbar)，T是大气层的绝对温度(单位：K)。

折射率N与大气压强、空气温度和水气压相关，在小范围区域内，折射率N可近似为水平均匀的。在垂直方向上，由于大气的气温和压强是随高度变化的物理量，所以N也随高度的变化而改变。通常情况下，折射率N随高度增加而减小。大量测试表明，大气折射率水平变化一般小于垂直变化的1～3个数量级[7]。

分析大气对雷达电波传播的折射影响时，必须有大气折射指数的模型。研究雷达电波大气折射效应时，通常忽略大气水平方向的变化，并视大气是球面分层的，从而折射率N可简化为仅随离地面高度H而变化的量[7]。

2.2 二次雷达在大气传播中的折射特性

目前，国内外各文献主要研究一次雷达在大气中的折射传播，对二次雷达在大气中的折射传播研究较少。二次雷达与一次雷达的体制不同，探测目标的机理、参数也不相同，因此大气折射距离误差修正模型也有一定的差别，如本文涉及的某型地面二次雷达在海口的检飞试验中测得1 000 m高度大气折射指数约为1.000 16，测得10 000 m高度大气折射指数约为1.000 3，这与雷达的常规模型是不一致的，因为二次雷达波长与一次雷达波长不同。因此，二次雷达的大气折射传播模型具有一定的特殊性。

飞机飞行时自身的高度测量是按照气压高度表指示的，飞机也是按气压高度飞行的，当一架飞机水平飞行时其气压高度表能稳定地指示某一常数。一次雷达测量飞机的高度是飞机相对于雷达站的高度，此高度数据在地球上空等压线上起伏变化[5]，而二次雷达获得飞机的高度是通过询问/应答的方式来间接获得飞机上的气压表高度数据(C模式高度)，这样，如果能找到匹配的大气折射模型，二次雷达更有优势根据气压高度来实时修正大气折射距离误差。

3 二次雷达大气折射距离误差修正方法

目前，二次雷达大气折射距离误差通常是按固定参数进行修正，如文献[8]提到大气折射指数为1.000 3，但这种方法只适用于对距离精度要求不高的场合，因为固定参数只解决了某一高度层的距离误差，而不适用二次雷达的整个高度层覆盖。文献[4]根据工程中的多次检飞数据，得到几种典型距离的修正曲线，给出了某一距离上不同高度层的距离修正量，具有一定的借鉴意义，实用效果也非常明显，但这种方法没有提出具体的二次雷达大气折射距离误差修正模型，这样将不同距离不同高度的修正量置入设备将会带来大量的工作量，也对设备的存储空间提出了更高的要求。

本文以经典的大气折射模型相关理论为指导，选取指数模型为大气折射率模型，忽略大气水平方向变化，利用大气球面分层思想，以离地高度为折射率的唯一自变量，根据大量工程应用中的检飞数据匹配各个高度层的最佳折射率，得出二次雷达在大气中的折射率为

(4)

式中：H为二次雷达获取的C模式气压高度(单位：m)。

构建了二次雷达的大气折射模型，再利用二次雷达能间接获得飞机气压高度的优势，就可以实时修正二次雷达的大气折射距离误差，以提高测距精度。具体步骤如下：

Step1 二次雷达须开启C模式询问，以获得飞机的气压高度。

Step2 将C模式气压高度代入公式(4)得到折射率N。

Step3 将折射率N代入公式(3)得到折射指数n。

Step4 将折射指数n、真空中的雷达波速度c代入公式(2)得到修正的雷达波速度v。

Step5 将修正的雷达波速度v、接收到应答脉冲相对于询问脉冲的间隔时间t代入公式(1)得到探测距离。

4 试验及结果

某型地面二次雷达按民航标准进行研制，测距误差小于29 m。在检飞试验中，检飞飞机、二次雷达都搭载和部署高精度差分GPS，以GPS数据为真值来标校二次雷达的位置(方位和距离)探测固定误差。检飞时，选取了1 000 m、3 000 m、6 000 m、10 000 m几个典型高度，距离覆盖从0～300 km。当以真空中的雷达波速度计算距离时，距离一次差(探测距离减去真值)结果如图1～4所示。

图1 真空条件1 000 m高度探测距离误差

图2 真空条件3 000 m高度探测距离误差

图3 真空条件6 000 m高度探测距离误差

图4 真空条件10 000 m高度探测距离误差

从图1～4可看出，以真空中的雷达波速度计算距离时，不同高度层的距离一次差都随探测距离振荡，呈锯齿状。1 000 m高度距离一次差振荡的幅度约为50 m，3 000 m高度距离一次差振荡的幅度约为50 m，6 000 m高度距离一次差振荡的幅度约为80 m，10 000 m高度距离一次差振荡的幅度约为40 m。造成不同高度层距离一次差振荡幅度不一样的原因是各高度层检飞的距离覆盖不相同。

以真空中的雷达波速度计算距离时的误差结果见表1。 从表1中可看出，当按固定参数修正距离时，各个高度层的一次差均值、标准差差别较大，10 000 m高度的测距精度(均方根误差)已经低于民航规定的精度[9]。

表1 真空条件各个高度层距离误差

一次差均值反映了设备本身的固有偏差，是可去除的，提高测距精度的有效办法是减小标准差。本文所描述的核心内容也正是通过建立大气折射距离误差修正模型将图1～4中距离一次差的振荡幅度减小或趋于直线。

按修正方法，重新计算某型二次雷达检飞数据，得到各个高度层的距离误差如图5～8所示。

图5 1 000 m高度下修正的距离误差

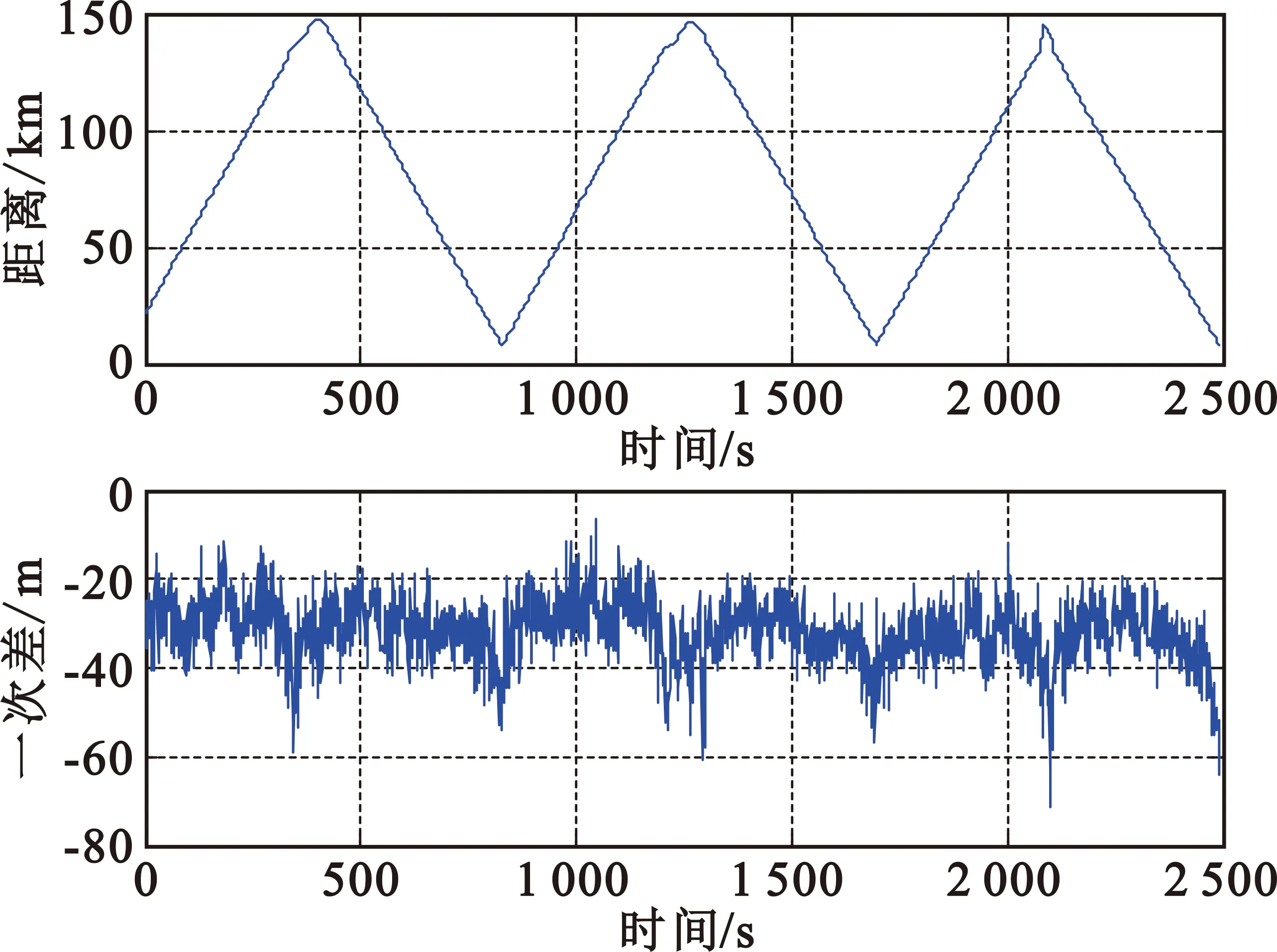
图6 3 000 m高度下修正的距离误差

图7 6 000 m高度下修正的距离误差

图8 10 000 m高度下修正的距离误差

从图5～8可看出，按修正模型计算距离时，距离一次差随距离振荡的趋势减弱，整体上看基本呈直线，局部仍然有小幅度振荡。这是由于不同地区的大气压强、空气温度和水气压是有差异的，同时也叠加了接收通道的热噪声、采样时钟等因素带来的随机误差。

修正后各个高度层的距离误差见表2。从表2中可看出，修正后该型二次雷达的测距精度保持在8 m左右，较修正前有显著提高。

表2 各个高度层修正后的距离误差

5 结 论

大气折射误差是影响二次雷达测距误差的主要因素。传统二次雷达在计算距离时通常用真空中的雷达波速度来计算，或用某一固定的经过修正的雷达波速度来计算，这样会带来一定的测距误差，或者只满足了某一高度层的测距精度而其他高度层测距精度仍然超标。某些二次雷达建立了大气折射距离误差修正曲线，但没有一个完整的二次雷达大气折射距离误差修正模型。本文分析了二次雷达的测距原理、电磁波在大气传输中的折射特性，以及二次雷达能间接获得飞机气压高度数据为大气折射误差修正所带来的优势，结合实际工程应用中的检飞数据，在大气折射指数模型的基础上提出了一种二次雷达大气折射距离误差修正方法。该方法以C模式气压高度为基准，能实时自动地计算任意高度层的折射率，从而得到修正的雷达波速度，减小了二次雷达测距中的大气折射误差，进一步提高了二次雷达的测距精度。该方法已成功应用于多个工程项目，效果显著。