变质岩等时线定年
李晓萌,程昊
同济大学 海洋地质国家重点实验室,上海 200092
1 放射性同位素地质年代学的历史沿袭和原理
地球科学是研究地球的现在和过去并展望未来的科学,其核心之一在于准确厘定事件发生的时间点和持续过程。放射性同位素地质年代学是最为理想的长周期地质时钟,可以说如果没有放射性同位素地质年代学就没有现代地质学的各项发现和理论变革,诸如磁场逆转、板块构造、恐龙灭绝之谜、月球探索、生命的进化、人类之源,更不用说地球和宇宙的年龄了[1]。
放射性同位素定年的起源可以追溯到1896—1902年间贝克勒尔和居里夫妇对于元素放射性的发现,随后卢瑟福和索迪对放射性衰变定律的发现大大推动了放射性同位素定年的发展。放射性核素以特定的速率衰变,基本不受外界温度和压力的影响。在一定的时间内,放射性核素衰变的数量与生成元素的数量之间有严格的比例。放射性核素衰变到原来数量的一半所需要的时间被称为半衰期。较长半衰期的放射性同位素体系可作测量地质时期长时间尺度的事件时钟,较短半衰期的体系则可作近期短时间尺度的时钟,从而准确厘定地质事件的绝对时间。
1.1 放射性衰变定律
放射性衰变是指不稳定的原子自发地发射出粒子和能量而转变为另一种原子的过程。各种不稳定原子的衰变有几种不同的方式,包括α衰变、β衰变、电子捕获衰变、核裂变以及同量异位衰变和分支衰变等。一些原子可以同时以2~3种不同的方式衰变,但是多数原子以一种特有的方式衰变。衰变的结果是母体同位素原子核的质子数或中子数发生变化,直到转变为稳定的子体同位素为止。
如果一个体系中初始的子体同位素原子数为D0,放射成因子体同位素的原子数为D*,衰变常数为λ,那么任意时刻t,该同位素的原子数D可以表达为初始原子数与放射性成因原子数的和,即:

以上方程是同位素地质学的基础。若t=0时体系中初始的子体原子数D0已知,则通过测定体系中目前的放射性母体的原子数和子体的原子总数,可求得体系封闭以来所经历的时间t,即:

放射性同位素定年法基于下面三个假设来建立:①子同位素的初始量是已知的;②被测岩石必须自始至终是完全封闭的体系,两种核素没有额外增加或者减少;③衰变速率始终不变。
1.2 等时线定年
我们已知放射性同位素定年需要满足以上三个假设,但是如果实际情况并不满足其中的一个或者几个假设,那么由此得到的年龄该如何解释?等时线定年法应运而生[2]。等时线法无需了解岩石中初始子同位素的数量,而是将子同位素与该同种元素的另一种同位素(非衰变产生)相比的比率作为测定的对象。对应上述方程式(1),即两边同除以一个稳定的非放射成因子体同位素S:


图1 等时线示意图:初始子体同位素比值相同,高、低母子体同位素比值的样品经历了相同的时间,将定义一条关于年龄的直线(修改自参考文献[1])
在初始状态下,等时线应该是一条水平的直线。随着衰变的发生,母体同位素逐渐减少,而子体同位素相应地逐渐增多,在等时线图中的反映是每个测量值以相同的速度向左上移动,样品之间的连线绕着其与y轴的交点(代表初始量的点)逆时针移动。一旦绘制出等时线,就可以根据直线的斜率得到样品的年龄。
根据等时线的定年原理,等时线的使用需要满足以下条件:①所选的样品具有同源性,即初始子体同位素保持平衡;②所选样品同时形成;③自体系形成以来一直保持封闭状态。这三个条件适用于所有等时线定年体系。
1.3 同位素质量分析仪
正如没有X射线就没有结晶学的发展,没有望远镜就没有天文学的发展,如果没有质谱仪的发明就没有同位素地质学的发展。1898年汤姆森发现了阴极射线和“阳离子射线”的本质,首次证明了氖具有两个原子量为20和22的同位素。随后1919年阿斯顿和登普斯特在汤姆森工作的基础上设计出了质谱仪,他们用这种仪器发现了周期表中大部分元素的天然同位素,并且测量了他们的质量和丰度。在之后的30多年内,质谱仪经过班布里奇和乔丹、尼尔和英格拉姆以及丘普卡等多人的改进,发展成为当时在物理、化学、生物研究中得到广泛应用的工具。近年来随着计算机和科技的发展,质谱仪的精度、性能和可靠性有了很大的提升,成为同位素测定不可或缺的一环。
质谱仪是在电磁场的作用下使带电粒子束按其质荷比值的大小进行分离,并分别进行测量的大型复杂装置。一台质谱仪由三个主要部件组成:①电离源区;②质量分析器;③离子收集器。自从阿斯顿发明第一台质谱仪以来,其各个部分都有了翻天覆地的发展,其中电感耦合等离子体(ICP)结合多接收器(MC)的质谱仪(MS)近年来已经成为同位素测量的主要工具。
2 等时线定年体系
变质岩中常用的等时线定年体系主要有Rb-Sr、Sm-Nd、Lu-Hf、Ar-Ar以及Pb-Pb体系。
2.1 Rb-Sr法
Rb有2个天然同位素,分别是稳定同位素85Rb和放射性同位素87Rb。Sr有4个稳定同位素,分别是84Sr、86Sr、87Sr和88Sr。在这4个同位素中,87Sr除了宇宙成因之外,还有部分是通过87Rb经β衰变生成的放射成因的87Sr。
根据衰变定律,Rb-Sr法测定年龄的基本公式为:

在变质岩Rb-Sr等时线法应用中,由于Rb具有较强的活动性,Rb-Sr同位素体系很容易遭到改造,要考虑因变质作用使得岩石局部或者全部重结晶而构成的新的岩石内部平衡。然而这时得到的年龄一般不能提供原岩形成年龄的信息,只能代表变质事件的年龄甚至是无意义的年龄,因此要针对不同情况具体进行年龄的分析判断。
2.2 Sm-Nd法
自然界中,Sm和Nd同属稀土族元素。Sm有7个同位素,其中具有放射性的是147Sm、148Sm和149Sm,但后两者半衰期太长(~1016a),在现有技术条件下其子体同位素的变化量无法准确测量,故目前不能成为定年方法。Nd也有7 个同位素,均为稳定同位素,其中143Nd为147Sm经α衰变形成的子体同位素。
根据衰变定律,Sm-Nd法测定年龄的基本公式为:


147Sm和143Nd同属稀土元素,具有十分相似的地球化学性质,这使得放射性成因的子体143Nd形成后很自然地继承母体147Sm在晶格中的位置。加之Sm、Nd具有很强的抗后期地质作用改造的特性,各种地质作用都很难使Sm和Nd发生分离和迁移,因而在岩石形成以后所经历的各种地质作用改造中,Sm-Nd体系常保持封闭状态,这一特点使得研究者们更青睐于使用Sm-Nd体系获得变质岩原岩的年龄信息。石榴子石是强烈富集重稀土元素的矿物,相对于全岩和其他大多数矿物具有较高的Sm/Nd比值,可以明显提高等时线年龄的精度,且在变质岩中保存较完好,是变质岩Sm-Nd法定年的重要矿物。
2.3 Lu-Hf法
Lu是最重的稀土族元素,有2个天然同位素:175Lu和176Lu。Hf是高场强元素,有6个天然同位素,分别为174Hf、176Hf、177Hf、178Hf、179Hf与180Hf,其中176Hf是由176Lu经过β衰变产生的,具有放射性。
根据衰变定律,Lu-Hf法测定年龄的基本公式为:

早在20世纪70年代,人们就认识到Lu-Hf同位素体系的应用前景,但是Hf具有比较高的电离能,使得Lu-Hf同位素的应用受到限制。直到20世纪90年代中期MC-ICP-MS技术的发展,使得Lu-Hf同位素的研究取得了重要的进展。目前变质岩Lu-Hf等时线法定年主要应用于高Lu/Hf比值的单矿物,石榴子石和磷灰石是两种主要应用的矿物,其他矿物(如独居石、榍石和磷钇矿)的结果也有报道。石榴子石是高级变质岩石中的主要常见矿物,它不但是变质岩温压计算的重要矿物,也是同位素定年的重要对象之一。由于石榴子石具有较高的母子体Lu/Hf比值、较小的矿物包裹体影响以及较高的封闭温度等特点,石榴子石样品的内部等时线法定年能够得到比其他等时线定年体系更准确的结果。
2.4 Ar-Ar法
Ar-Ar法是在K-Ar法的基础上产生的。众所周知,常规K-Ar法和40Ar-39Ar法定年都需要对存在的氩进行校正,而校正的前提是36Ar全部来自大气,且大气中氩的40Ar/36Ar比值为295.5。但是,这个前提往往是很难满足的,因为在矿物或者岩石形成的时候可能会有继承氩,其40Ar/36Ar与现代大气氩相比明显不同,会产生较大误差。
当继承氩中的40Ar/36Ar比值大于或者小于295.5,很容易造成放射性成因40Ar的过量或者不足,继而影响定年准确度。而采用40Ar-39Ar等时线法可以有效地解决继承氩的问题。
样品逐步加热过程中释放气体的40Ar/39Ar比值为:

式中下标c代表混染氩,它包括大气氩和矿物中的继承氩。上式可进一步写成


运用等时线法解决年龄问题的前提是39Ar/40Ar数据必须来自地质上同时形成的样品,且这些样品具有相同的40Ar/36Ar初始比。
理论上,含有K元素的矿物和岩石都可以用于Ar-Ar法定年,例如云母、角闪石、辉石和长石等矿物。在变质岩定年应用中,要注意按照最终定年的目的来选择合适的样品。对于确定构造事件或者变质作用发生的时间,一般从受到强变质作用和构造作用的岩石样品中分选出Ar同位素封闭温度较低的矿物来定年;对于确定变质岩原岩形成的时代,一般从受到后期变质作用较小的岩石样品中分选出Ar同位素封闭温度较高的矿物来定年。
2.5 Pb-Pb法
U有3种天然同位素,分别为238U、235U和234U,其中238U和235U经放射性衰变分别形成稳定同位素206Pb和207Pb,而234U为238U衰变的中间产物。Th由2个同位素组成,分别为232Th和230Th,其中232Th经放射性衰变形成稳定同位素208Pb,而230Th丰度极低,亦为238U衰变的中间产物。
Pb由4个同位素组成,分别是204Pb(1.4%)、206Pb(24.1%)、207Pb(22.1%)和208Pb(52.4%)。206Pb、207Pb、208Pb为稳定同位素,分别为238U、235U、232Th放射性衰变形成的子体同位素。204Pb因无对应的放射性同位素母体,故不属于放射成因同位素。
根据衰变定律,在封闭体系中,238U向206Pb的衰变表达为:

Pb-Pb等时线法不再受样品中近期铀或者铅的丢失所影响,而只要求所有样品有同样的年龄和同样的初始铅同位素比值,并且这些样品直到受到近期的化学风化作用之前都保持封闭体系。
3 影响等时线定年准确度和精度的因素
我们都知道抛开误差而单纯地论结果是没有意义的。由于等时线法定年得到的是绝对年龄,我们除了关心年龄的准确性和精度以外,定年的误差往往比最终的结果更重要。等时线年龄的误差包括随机误差和体系误差。随机误差指与等时线假设的偏差以及质谱分析的不确定性,决定了测量值的“精确性”。随机误差相对于测量值的算术平均值有一个“正态”分布或者高斯分布,而随着测量次数的增加,算术平均值趋近于真值。体系误差指衰变常数等因素,决定了测量值的“准确性”,是真值与一组测量值之间的一致的差别。
3.1 测试误差传递
根据等时线定年的基础公式,由误差传递公式,可得绝对误差为:

3.2 衰变常数误差
衰变常数是放射性同位素定年不可或缺的一环。在放射性同位素定年中,最重要的是准确知道各个定年体系母体放射性同位素的衰变常数,但其实衰变常数远非常数。
衰变常数的测定主要有两种方法:第一种是利用电离室和液体闪烁计数仪进行计数,例如20世纪30年代初对于147Sm-143Nd体系衰变常数的测定,但是由于147Sm长达1011年的半衰期,很难排除误差获得最接近真实值的衰变常数;第二种方法是年龄对比法,要获得147Sm的衰变常数,可以利用两个不同的定年体系对已知年龄的样品进行对比定年,其中用于对比的定年体系应该是公认为较准确的,例如通过U-Pb体系确定Sm-Nd体系衰变常数。但是利用这种方法获得衰变常数也存在明显缺陷,会受到体系后期扰动和参照体系本身半衰期准确度等方面的影响。因此,目前地球化学界所公认的衰变常数并不是一个永远也不会改变的“常数”,只是通过多个不同样品以及不同定年体系所验证出来的近似真值的值。
在等时线定年中,一直把衰变常数当作一个“常数”意味着忽视其不确定性引起的体系误差,而在地质年代学日益高精度化的今天,考虑衰变常数的不确定性对于对比和解读同一样品不同定年体系的年龄差异有很重要的意义。
对前面提到的式(16)进行简化,若只考虑衰变常数误差,而忽略由于同位素比值测定引起的误差,可得到下面式子:

由(17)可得到年龄误差与实际年龄关系图(图2)。

图2 各体系衰变常数的不确定性引起的年龄误差与实际年龄关系图
如图2所示,等时线定年体系的误差随着实际矿物或事件年龄的增大有增长的趋势[3]。Lu、Sm衰变常数的不确定性引起的年龄误差最为明显,仅由此引起的Lu-Hf 年龄误差由 1 000±4 Ma 增加到 4 600±20 Ma,Sm-Nd 年龄误差由1 000±7 Ma增加到 4 600±35 Ma。然而,87Rb-87Sr、238U-206Pb和235U-207Pb体系中衰变常数误差比实验随机误差小得多,可忽略不计。
在相同定年体系年龄对比中,无论是同一样品还是不同样品,衰变常数带来的误差会使得两个年龄偏大或者偏小相同的幅度,这种情况下可以不考虑衰变常数传递误差。然而,在不同体系的年龄对比中,衰变常数传递误差往往不可忽视。如图3所示,样品的Lu-Hf年龄为202±2 Ma,Sm-Nd年龄为196±2 Ma。如果不考虑衰变常数误差,这两个年龄是有显著差别的;当考虑衰变常数误差时,两个年龄分别为202±2.8 Ma和196±3.5 Ma,将产生年龄重叠的现象,难以区分。最终得到的结果也从前者的两个不同地质事件,变为后者的单一地质事件[4]。

图3 衰变常数的不确定性对不同定年体系年龄的影响:(a)衰变常数误差对定年结果的影响 (λ147Sm=(6.54±0.05)×10-12a-1(1σ)[5],λ176Lu=(1.867±0.013)×10-11 a-1(1σ)[6-7]);(b)黑色部分表示不考虑衰变常数误差影响的年龄值,延长的灰色部分表示加入衰变常数误差后的年龄值。前者是两个具有显著性差异的年龄,后者则表现为在误差范围内是一致的两个年龄。修改自参考文献[4]
3.3 稀释剂
同位素的分析测定一般采用同位素稀释法。其原理很简单,就是通过向待分析样品中加入已知量的待测元素的某一富集元素,使其与样品中的同位素混合均匀,从而能够改变样品中的待测元素的同位素的丰度比,最后再用质谱法测定混合后样品的同位素比值,即可确定待测元素在样品中的浓度。
同位素稀释法作为一种高精度、高效的测定方法,了解其误差对于得到准确的等时线年龄至关重要。
稀释剂的相对误差公式表示为:
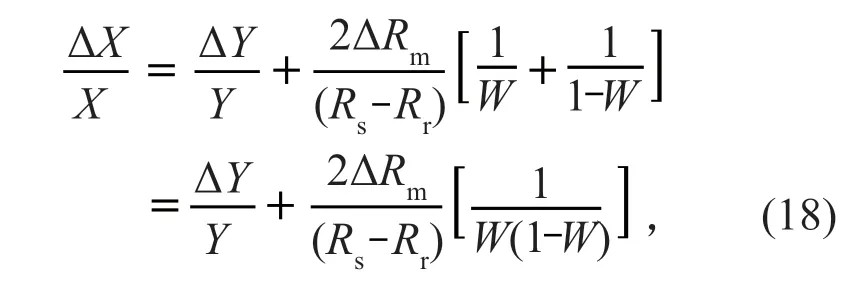
式中Rs、Rr和Rm分别代表稀释剂、样品以及两者混合后的已测量同位素比值,X和Y分别是样品和稀释剂中的待测同位素比值,W=X/(X+Y)是样品中待测同位素占混合后溶液的待测同位素的比值。
由式(18)可得,要使相对误差最小,则Rs-Rr要达到最大,那么稀释剂的同位素与样品同位素的差别尽可能地大。此外,对给定的Rs和Rr,W(1-W)要达最大,则W=X/(X+Y) = 0.5,也就是所称取的样品和所加的稀释剂中目标同位素的量要尽可能相等(图4)[1]。
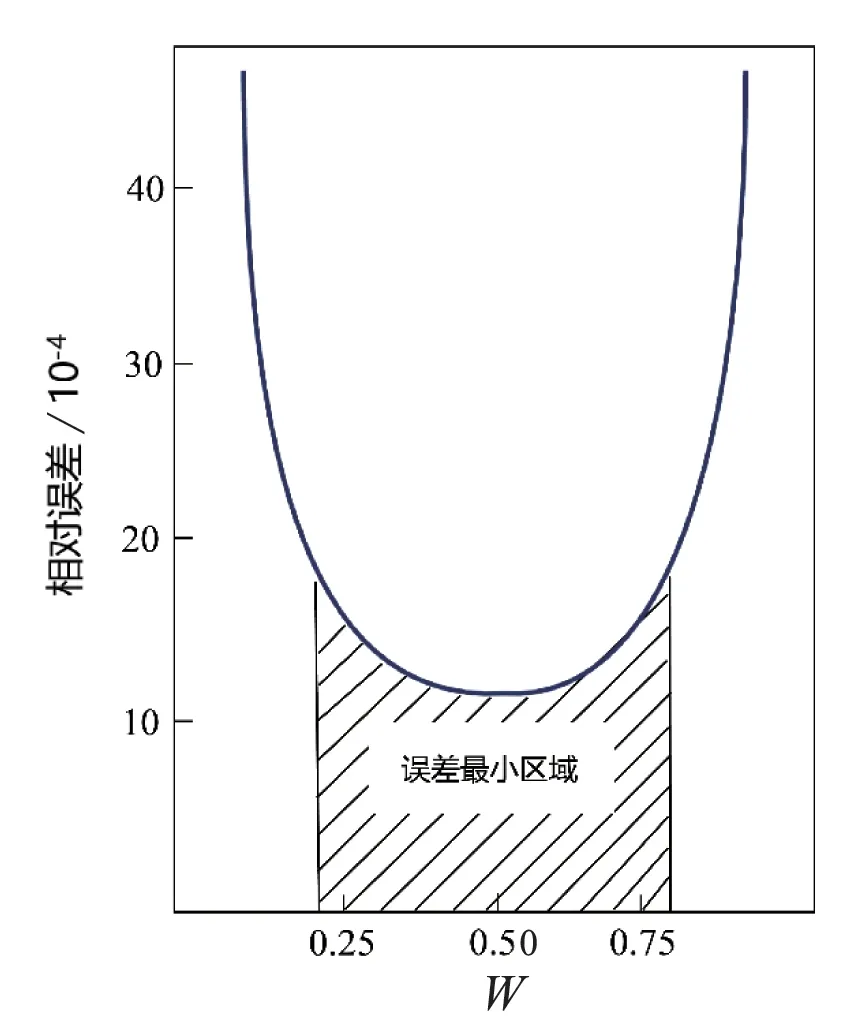
图4 同位素稀释引起的相对误差与比值W的相关函数图。图中区域部分误差最小(修改自参考文献[1])
除了以上未能达到最佳稀释比引起的误差之外,稀释剂带来的误差还可能有以下方面:
(1)标定稀释剂溶液中产生的误差,可能来源于含稀释剂化合物的可能的非化学计量成分,或者是用质谱仪分析稀释剂同位素时发生的分馏,也可能是称量和稀释稀释剂时引起的误差;
(2)混合物同位素比例的测量值可能受到质谱仪中分馏的影响,而且如果元素中仅有两个天然同位素,则这个误差不能修正;
(3)某些地质样品中要测量的元素处于难溶的矿物中,使得元素与稀释剂没有完全混合,引起测定误差;
(4)由于水的蒸发或者元素被吸附在储存稀释剂的容器壁上,稀释剂溶液的浓度随时可能发生改变。
3.4 地质复杂性
因为石榴石是应用最为广泛的等时线定年对象,下面就以石榴子石Lu-Hf和Sm-Nd体系为例来阐述由地质样品复杂性导致的等时线法的诸多不确定性的几个方面。
石榴子石生长历史复杂且受到后期元素扩散的影响,而这些过程可能都会影响等时线假设的有效性,因此合理地分析可能的影响因素并解释等时线的准确性就显得尤为重要。下面是可能影响等时线年龄的一些因素。
3.4.1 初始子体同位素不平衡
之前已经提到,构建准确等时线的前提是要保证所选矿物之间的初始子体同位素达到平衡状态。石榴石的生长具有阶段性,不同阶段有着不同的反应矿物,从而也会留存有相应的同位素组成特征。尤其是反应矿物中包含有极度富集Lu或者亏损Lu的副矿物时,生成的石榴石与全岩的初始子体同位素比值相差较大,这将导致初始的等时线就具有负斜率或者正斜率(图5),最终得到偏年轻或者偏年老的等时线年龄[4]。

图5 石榴子石继承反应矿物子体同位素特征及对等时线年龄的影响
大部分岩石中普遍存在着初始子体同位素不平衡现象,但是当初始子体同位素与全岩组成之间的差异较小,且定年矿物具有较高的母子体比值,在经历了较长时间的演化后,这种初始子体同位素不平衡带来的不一致可以在一定程度上抵消,同样可以获得高精度且准确的年龄。
3.4.2 包裹体的影响
变质石榴石的形成过程可能包裹早期形成的矿物,例如含有大量稀土元素(REE)的褐帘石、磷钇矿和磷灰石,含有高Hf的锆石和金红石等,还有其他固相包裹体如单斜辉石、角闪石、绿泥石和云母等。这些常见包裹体矿物的存在会影响真实的石榴石Sm-Nd和Lu-Hf同位素比值,而在样品处理初期全部溶解的方法将得到不准确的同位素比值,从而得到没有明确地质意义的混合年龄。对于Lu-Hf体系,当石榴石中存在锆石包裹体时,由于锆石中的Hf浓度是石榴石中Hf浓度的近10万倍,如果锆石包裹体的年龄比石榴石年龄老得多,则它们的存在会显著降低所测量的石榴石的176Hf/177Hf值,得到错误的年龄。当全岩中混入锆石包裹体时,同理,也会得到错误的年龄[8](图6)。
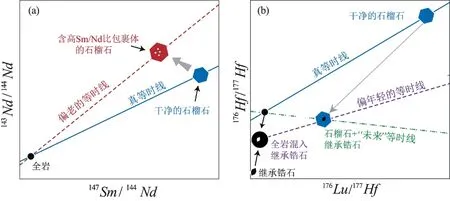
图6 包裹体矿物对石榴石不同定年体系等时线的影响:(a)包裹体矿物对石榴石Sm-Nd等时线的影响;(b)包裹体矿物对石榴石Lu-Hf等时线的影响(据参考文献[9]修改)
因此,在测试过程中要尽可能地去除包裹体。溶样前,人工挑选去除可见包裹体;溶样过程中,常常采用“选择性溶解”的方法[9],利用不同矿物在不同浓度、不同类型酸溶液中的溶解性质的不同,在完全溶解石榴石的同时尽量去除难溶包裹体,从而将包裹体的影响降到最小。
3.4.3 石榴石年龄的扩散重置
变质岩中的石榴石一般形成于400°C以上的温度,并且能够在超高温甚至大于1 000°C的条件下持续生长。如果石榴石在形成后继续经历升温,温度达到Lu-Hf和Sm-Nd体系的封闭温度以上,则定年体系开放,石榴石年龄会被完全或部分重置[10]。
对同一个石榴石样品进行耦合Lu-Hf和Sm-Nd定年,得到的Lu-Hf年龄通常会比Sm-Nd年龄大,这可以用石榴石中Lu-Hf系统的封闭温度高于Sm-Nd系统的封闭温度和几何效应来简单解释[11],但是还要考虑元素扩散重置的影响。一般来说,如果石榴石在生长过程中被持续加热或者经历了长时间的冷却历史,扩散重置会使得最终得到的年龄偏小。然而对于Lu-Hf体系,由于Lu在石榴石中具有高度相容性,在生长过程中会产生中间高、边缘低的钟形生长环带,随后随着176Lu的衰变形成类似的钟形176Hf/177Hf内生长环带,从而在石榴石内部可能保留了大量的生长初期放射性176Hf,得到比真实年龄老的Lu-Hf年龄。
我们对龙游石榴角闪岩进行了多同位素定年研究,发现Lu-Hf和Sm-Nd年龄相差约70 Ma[12]。两体系间的差异可以解释为石榴石在峰期变质温度下REE和Hf完全重新平衡,并在随后发生快速冷却,保证体系的封闭;但是石榴石中广泛存在的微裂隙使得有效的扩散半径大大缩小,导致Sm-Nd体系在之后的热事件里被部分重置(图7),从而造成两定年体系的年龄差。
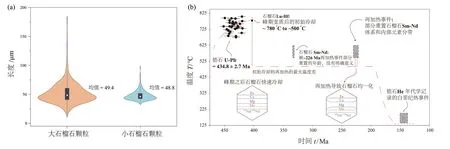
图7 石榴石年龄与颗粒大小相关的扩散重置:(a)石榴石内部裂隙尺度分布;(b)石榴石生长的T-t过程的时间和事件记录(据参考文献[12]修改)
4 总结和展望
近年来,变质岩等时线年代学不论在方法学上,还是在具体的应用上,都得到了飞速发展。它为确定变质岩演化的绝对时间提供了越来越准确和精确的约束。不远的将来,提高对极少量样品的分析准确性和精度,将是国际上几个一流实验室面临的挑战。这不仅要求高稳定、高精度和高检出限的仪器搭配,也需要对现有或新发展的标准物质以及稀释剂进行更准确和精度更高的标定或配比,还需要更高效的配合特定体系的有效流程的建立。一方面需要在对样品进行微区原位取样方法开发的同时,保证包裹体矿物的有效去除;另一方面需要扩大每个体系的定年对象和对同一对象的耦合多体系定年。再者,获得更高精度的衰变常数将一直是科学家为之努力的目标。结合单颗粒定年、岩相学观察、矿物微区元素分带和热力学模拟来获取寄主岩石的构造热演化历史的变质岩系统研究范式可望在未来几年成为变质岩研究的标准模式,从而彻底改变以往矿物、岩石和年代学分立研究的样式。
(2021年6月14日收稿)■

