数字签名和认证技术课程的渐进式教学案例化设计*
张艳硕 刘天宁 李梦东
北京电子科技学院,北京市 100070
1 引言
随着信息技术的大规模应用和数字经济的加速发展,信息安全问题日益突出[1],其核心技术基础之一的数字签名和认证技术,被广泛地应用于军事、通信、电子商务和电子政务等领域,它在身份认证、数据完整性和抗否认等方面具有其它技术无法替代的作用。 数字签名和认证技术课程是《密码学》专业基础课的必要延伸,是信息安全类课程所用认证技术的更为全面和深入的介绍。 本课程在实际教学过程中面临着理论知识范围广、知识交叉多元化、应用前景广泛、实践性强等特点。 因此, 如何设计数字签名和认证技术课程的教学内容, 如何改善课程的教学方法一直是今后需要持续研究的问题。
渐进式教学法是我国传统的教学方法,它产生和形成于我国深厚的文化背景中[2]。 循序渐进是渐进式教学法的要旨。 渐进式教学具有内容上由浅入深、由易到难的特点,便于学生学习、理解、掌握和综合运用[3]。 从简单到复杂的普遍认知规律和实验教学规律是渐进式教学需要具备的规律。 渐进式教学方法已经在众多学科教学中应用,其实用性已经得到较为充分的证实。
目前,数字签名和认证技术大多作为密码学课程教学的一部分,在教学中往往较少进行较为深入的学习,针对数字签名和认证技术的教学内容主要集中在签名算法和认证技术的简单介绍,然而数字签名和认证技术的重要性日益凸显,同时本课程的教学是一个层次分明的渐进过程,目前数字签名和认证技术教学领域还没有较为系统的渐进式教学模式的提出。
数字签名和认证技术课程应采用循序渐进、层次递进并结合具体案例的方式进行渐进式案例化教学。 首先将课程分为理论、应用和实践这三个部分,以知识层次递进的方式渐进的教学相应知识。 然后再将每个部分的知识从较为基础知识讲起,再在其基础上循序渐进地教授较为综合的相关知识,这样符合渐进式教学的普遍规律。 在理论上,主要涉及基础签名算法和认证协议的介绍;在应用上,主要涉及具有附加功能签名和认证协议的各种具体方案和分析方法,以及它们在不同场合的应用;在实践上主要涉及在实际密码系统中具有较好适用性的签名和认证协议的相关知识。
本文旨在提出数字签名和认证技术课程的渐进式教学案例设计,用实践性、教学性强的案例,由浅入深,循序渐进地去讲解数字签名和认证技术的理论知识和实际应用。 渐进式教学案例设计作为一种较为新颖且实用的教学方法,能让学生直接、快速掌握更多的数字签名和认证的知识,更好地培养学生的应用实践能力,为培养从事密码与信息安全类领域的人才做好相关知识的储备以及学习方法的拓展,从而更好地适应密码应用技术快速发展的大环境。
本文首先介绍数字签名和认证技术在理论方面的渐进式教学案例,其次是在应用方面的渐进式教学案例,然后介绍在具体实践中的渐进式教学案例,最后介绍课程教学中的实践经验。
2 数字签名和认证技术课程的基本特征
2.1 课程理论知识范围广
数字签名和认证技术是一门理论知识内容多,覆盖面非常广泛的课程。 同时也是理论难度大,实践性和应用性均比较强的课程。 故本课程的学习需要很多前置课程作为基础, 前置课程包含密码学、信息安全数学基础等。 前置课程的知识量大、难度高, 体现出本门课程对数学和密码学基础的要求。 目前数字签名和认证技术在理论和实践上己经形成了丰富的知识体系,因此需要掌握的相关知识也非常广泛。
2.2 课程的知识交叉多元化
从课程内容的联系上讲, 数字签名和认证技术可以说是多个学科的一个交汇点, 这些学科包括:密码学、概率论、近世代数、密码学应用技术等。 从应用数学的角度看, 数字签名和认证技术是计算数论、抽象代数等理论的一种应用[4];从通信的角度看, 数字签名和认证技术是保密通信和通信网络安全的研究内容;从计算机应用的角度看, 数字签名和认证技术是数据安全、计算机安全和网络安全的研究内容。 数字签名和认证技术的研究内容决定了它的交叉性和多元化, 这使数字签名和认证技术从不同的方面得到研究, 从而得以不断发展。
2.3 课程应用前景广泛
密码法的颁布为签名算法和认证技术的发展保驾护航。 签名算法和认证技术及其应用的不断发展与革新,使得课程的内容更加实用,课程的知识更加丰富,课程的应用前景更加广泛。因此课程的教学应做到与时俱进,为学生提供最新签名算法和认证技术的相关知识以及获取最新知识的渠道,利用最新文献资料对相关问题做进一步的研究,有效拓展学生的知识面。
2.4 课程实践性强
目前,数字签名和认证技术已广泛应用于商业、金融和办公自动化等系统中,同时作为一种密码学的基础构件,成为安全电子商务和安全电子政务的关键技术之一[4]。
数字签名和认证技术课程的基本目的在于让学生掌握数字签名和认证技术的基础知识并加以实际应用。 因此,我们需要重视实践教学,让学生在完成本门课程的学习后可以较为熟练的掌握签名算法和认证协议的实际应用。 因此课程的教学不应局限于基础算法以及协议的讲解,还应强化其实践性。
3 数字签名和认证技术渐进式理论教学案例设计
从本质上讲, 本课程的主要内容是一些具体的签名算法和认证协议,由此可见数字签名算法和认证协议的基础理论知识对于本课程的重要性。
3.1 DSA 及其标准化DSS 算法的渐进式教学
在进行数字签名内容的教学时,同学们往往对DSS 签名标准和DSA 算法分不清,采用渐进式教学方法可以让同学们在了解签名算法后更有效的学习基于这种算法的签名标准[3]。
DSS 数字签名标准使用的算法称为DSA,它是在ElGamal 和Schnorr 两个方案基础上设计出来的。
DSA 算法如下:
(1)全局公钥K:p,q,g。p,q,g作为系统参数,供所有用户使用,在系统内公开。
(2)一个长度为L比特的大素数P,L的大小在512 到1024 之间,且为64 的倍数。
(3)q是能被p-1 整除的160 比特的素数。
(4)一个q阶元素g∈。g可以这样得到,任选h∈;如果h(p-1)/qmodp>1,则令g≡h(p-1)/qmodp,否则重选。
(5)一个用户随机选取的整数x∈, 并计算出y≡gxmodp。
(6)一个HASH 函数(SHA-1)H:{0,1} →Zp。
(7)对消息M 生成数字签名时,随机选取一个 秘 密 整 数 k ∈Zp, 计 算 出r≡(gkmodp)modq;s≡k-1(H(m)+xr)modq, 输出(r,s)为签名人对M 的签名。
(8)检查r和s是否属于[0,q],若不是,(r,s)不是签名。
( 9 ) 计 算t≡s-1modq,r′ ≡(gh(m)tmodqyrtmodqmodp)modq。
(10)比较r’=r 是否成立。
我们在完成DSA 算法的学习后可以对基于它的签名标准DSS 更好地进一步学习,我们将具体的DSA 算法结合DSS 框架基础进行讲解,让学生更好理解签名标准的算法以及签名标准,为学生之后学习签名标准提供良好思路。 通过表1 我们来渐进学习DSS 和DSA 算法。

表1 DSA 算法和DSS 的渐进式对比
在进行DSA 算法及DSS 标准的学习时,我们先介绍DSA 算法的签名验签过程以及算法具体流程,在掌握算法的基础上,循序渐进的学习基于DSA 算法的DSS 签名标准。 渐进式教学为我们学习签名算法及其标准提供了新的方法。我们在介绍其签名算法具体过程的基础上,将具体签名算法步骤与签名标准的模型及基础框架相对应,以此来渐进学习基于这种签名算法的签名标准。
3.2 OSS 及其改进ESIGN 算法的渐进式教学
我们也可以采用渐进式教学的方法来学习数字签名体制及其改进的签名方案。 OSS 签名体制以及ESIGN 签名方案就是很好的案例。 采用渐进式教学方法可以让同学们在了解签名体制后更有效的学习基于这种签名体制的改进方案。
OSS 签名体制是由Ong、Schnorr 与Shamir于1984 年所提出,但在1987 年被证明为不安全,直到1993 年才有人提出一个安全的改进方法[5]。
ESIGN 是由Okamoto 和Sharaishi 在OSS 的基础上提出的数字签名方案。 ESIGN 是日本NTT 院士Tatsuaki Okamoto 于1990 年提出的[6]。
我们首先学习OSS 签名体制,在学习OSS签名体制后,通过表2 来进一步深入学习基于OSS 签名体制改进版的ESIGN。

表2 OSS 和ESIGN 的渐进式对比
在进行OSS 签名体制及ESIGN 方案的学习时,我们先学习OSS 签名体制,在掌握签名体制的基础上,循序渐进的学习基于OSS 签名体制改进版的ESIGN 并分析比较两者区别从而渐进学习这两种签名方案。 渐进式教学为我们学习签名标准及其改进方案提供了新的方法。 在教学时,我们通过比较两种签名体制在签名参数初始化、签名验签过程、签名安全性、发展情况以及应用等方面来进行渐进式教学。 日后,在进行两种数字签名体制教学,尤其是一种是另外一种的改进版时,我们可以继续使用渐进式教学的方法。
3.3 Needham-Schroeder 协议及其改进协议的渐进式教学
认证技术在理论上的教学内容主要在于认证协议的安全性和构造理论,Needham-Schroeder协议及其改进协议可以作为学习认证技术理论的案例。
Needham 和Schroeder 提出了一个十分著名的安全协议[8], 即NS 私钥协议。 1981 年Denning 和Sacco 指出了NS 私钥协议的一个错误, 并提出了Denning-Sacco 协议来对NS 私钥协议进行改进, 但是Denning-Sacco 协议同样存在问题。 2006 年Deng 等人针对原始的NS 私钥协议的缺陷进行了改进。
在教学中, 我们首先学习 Needham-Schroeder 协议,然后在分析其安全性缺陷,最后学习改进后的协议。 通过表3 我们来渐进学习Needham-Schroeder 协议、安全缺陷以及解决方案。

表3 Needham-Schroeder 协议及其改进协议的渐进式对比
在进行其他认证协议的理论教学时,我们可以继续采用渐进式教学的方法,首先介绍认证技术的最基础协议,进而初步了解认证协议的基本框架,然后通过分析协议可能存在的安全威胁来更加深入的认识哪些因素或步骤影响认证协议的安全性,最后我们再学习针对安全问题提出的改进协议,从而让学生更加直观感受到认证协议的构造理论以及改进措施,为将来学习类似协议提供一种思路。
4 数字签名和认证技术渐进式应用教学案例设计
随着数字签名和认证技术的不断发展和进一步深入研究,数字签名和认证技术的知识和应用不断更新换代,数字签名和认证技术在应用上从小规模的商业和个人数据保护开始,伴随着互联网和电子商务的发展,到今天已经发展成为数字社会的安全基石之一[9]。 本课程也应该做到与时俱进,有必要向同学介绍一些基础以及较为新颖的数字签名和认证技术的应用知识。
4.1 基于身份的数字签名的渐进式教学
数字签名在对信息安全系数要求较高的领域中应用广泛,比如在电子商务、电子政务、电子投票等领域。 一般的数字签名是通过数字证书来进行管理,其核心是数字证书机构CA,自然就会存在证书存储、证书管理和证书托管的问题,这些问题会导致系统成本高昂,管理复杂。 为了解决出现的问题,提出了基于身份的数字签名[10]。 基于身份的数字签名也是近几年密码学领域中研究的热点。 学习基于身份的数字签名可以拓宽学生数字签名应用知识层面的深度和广度。
1984 年Shamir[11]提出基于身份的加密、签名、认证的设想,其中身份可以是用户的姓名、身份证号码、地址、电子邮件地址等。 基于身份的密码系统不存在传统CA 颁发证书所带来的存储和管理开销问题。
签名的性能往往影响乃至决定签名算法能否有更好的实际应用前景,要判断一个基于身份的数字签名方案其性能的好坏主要有三个标准[10]:(1)数字签名与系统公开参数的长度;(2)签名与验证过程的计算复杂性;(3)方案的安全性。 然而往往签名与验证过程的计算复杂性的分析在教学过程中被忽视。 Cha-Cheon 和Hess 这两个签名在系统建立以及密钥生成都没有区别,但在签名与验签过程中的运算不同使得两者在计算复杂性有了较大差异,进而影响两者的方案效率,这两个方案可以作为我们学习数字签名性能的渐进式案例。
2002 年Jae Choon Cha 与Jung Hee Cheon 以及Florian Hess 分别发表采用双线性对构造的基于身份的数字签名算法 Cha-Cheon[12]和Hess[13]。 Hess 方案的效率要比Cha-Cheon 方案高很多。 我们通过表4 来渐进学习签名与验签过程中的运算对方案效率的影响。

表4 Cha-Cheon 和Hess 的渐进式对比
在教学中,我们首先对Cha-Cheon 方案在签名和验签的运算进行分析,因为在计算的时候,双线性映射对的计算D,G1上的一次标量乘运算M,最为耗时,所以就以D 和M 做为比较标准。 在完成Cha-Cheon 方案运算分析后再和Hess 方案进行比较,在签名过程中,Hess 方案中的对运算因为与签名消息无关,用户可以预计算,Cha-Cheon 方案与Hess 方案效率基本相似。在验证的过程中,Hess 方案中的对运算与消息也无关系,同样可以预计算,因此比Cha-Cheon方案少一个对运算,效率也就高了很多。 由于双线性对计算代价最大,所以在签名和验证过程中所包含的对的计算越少越好。
数字签名的方案效率对于评判一个签名算法的性能具有重要意义,因此我们在以后进行教学时,通过表格对比基础算法在签名验签进行运算的种类以及数量,例如对运算,点加运算、数乘运算、杂凑运算、乘法运算、指数运算等等来渐进判断他们方案效率的优劣。 在教学时,我们通过分析对比签名验签具体运算过程的不同造成的方案效率不同来让学生思考分析影响签名效率的具体因素,为学生今后继续学习、分析乃至设计签名算法提供一个重要思路。
4.2 基于离散对数的数字签名的渐进式教学
1985 年,T.ElGamal 提出了基于离散对数的公钥加密和签名方法,并奠定了离散对数密码学基础。 从那时起,围绕离散对数系统产生了不少研究成果,离散对数也被誉为当代密码学领域的三大基础之一。 因此,学习基于离散对数的数字签名对于本课程显得十分重要。
(1)EIGamal 与Schnorr 方案的渐进式教学
基于有限域上离散对数问题的公钥加密体制,最著名的是EIGamal 加密体制。 Schnorr 数字签名方案是ElGamal 型签名方案的一种变形,ElGamal 型签名方案定义中已经把它作为一种类型,该方案于1989 年由Schnorr 提出。
由于ElGamal 型签名方案拥有多种变形方案,Schnorr 作为其中一种较为重要的变种方案值得我们进行深入学习,同时学习这两种算法也对学生初步了解基于离散对数的数字签名及其变种算法起到较好的引导作用。 我们通过表5来渐进学习这两种签名算法。

表5 EIGamal 和Schnorr 的渐进式对比
在进行基于离散对数的数字签名的基础教学时,我们首先学习EIGamal 的签名验签过程,其次对比学习Schnorr 算法的签名验签过程,然后根据两者签名验签的过程来分析两者在安全性、长度以及速度的差异。
在教学过程中,我们通过比较EIGamal 与Schnorr 方案在签名验签过程的差异来渐进分析两者在安全性、签名长度、运算速度等方面的不同,这为我们后续学习更加复杂的离散对数签名打好了基础,也为我们学习离散对数签名及其变种提供一种方法。
(2)EIGamal 及其推广方案的渐进式教学
Harn 等人[14]对ElGamal 及其类似方案进行了总结,给出了18 个安全可行的方案,称之为广义ElGamal 签名方案。 方案, 称之为广义ElGamal 签名方案。 描述如下:
1)初始过程
设p是一个大素数,整数g是有限域的本原元,h是一安全的哈希函数,系统中用户A的私钥为x(1xp-1),相应的公钥为y≡gxmodp。
2)签名过程
对于待签消息m,签名者A任意选取一个随机整数k(1kp-1),满足gcd(k,p-1)= 1,计算r=gkmodp。 签名方程的一般模型为
其中(a,b,c)为(h(m),r,s)的一个置换,由签名方程解出s,则(r,s)为消息m的签名。
3)验证过程
接收方收到m和签名(r,s)后,验证ya≡rbgcmodp是否成立,如果成立,则接收签名,否则,拒绝签名。
ElGamal 型签名方案的推广问题,其实是签名方程的参数选取问题。 学习基于离散对数的数字签名的推广方案可以让学生更加深入、具体学习ElGamal 型签名方案,不仅让学生更好认识数字签名理论的基础知识,还可以做到以点带面,通过分析签名算法中a,b,c三值的不同,进而具体学习更多离散对数签名,为学生日后深入研究该领域签名算法打好基础。 在教学时,我们通过表6 以对比的方法来渐进学习下述算法。基于离散对数难题的各种数字签名方案,这部分内容对于刚开始接触数字签名的同学们而言是相对容易的,也是必须掌握的基本知识,相信通过循序渐进的方式学习,同学们会从中感悟数字签名的奥妙,并产生继续深入学习的兴趣。离散对数用于数字签名的优势在于其指数运算的化简和处理比其他运算相对简单,很容易构造不同的方案,因此,签名方案的资源相当丰富。通过渐进式案例教学则可以让学生在学习时更加快速掌握离散对数数字签名的多种构造方法,为以后深入学习研究相关签名做出必要准备。

表6 签名算法中a,b,c 的取值

表7 不同参数模式的签名方案
4.3 基于挑战应答身份鉴别协议的渐进式教学
挑战应答身份鉴别协议通过向验证者展示与证明者实体有关的秘密知识来证明自己的身份,但在协议中并没有向验证者泄露秘密(私钥)本身。 挑战应答身份鉴别协议作为身份认证技术的一种在实际应用中被广泛采用。 在教学中我们以表8 为例进行渐进式教学。

表8 基于挑战应答身份鉴别协议的渐进式对比
在教学过程中,我们首先学习基于对称加密的挑战应答身份鉴别协议,在了解其单向认证以及双向认证的基础上,渐进学习基于消息认证码、公钥加密、数字签名等其他类型的身份鉴别协议,同时巩固之前学习的相关密码学知识。 日后如果也有类型单项认证以及双向认证的教学内容,我们同样可以根据上述表格进行修改,从而渐进学习挑战应答身份鉴别协议。
5 数字签名和认证技术渐进式实践教学案例设计
数字签名和认证技术在实践中往往作为密码系统的重要组成部分。 本课程也应向同学介绍一些实用且具有发展前景的实践知识。
5.1 签密体制和方案的渐进式实践教学
密码系统提供的基本安全服务有机密性、完整性、认证和不可否认性。 在密码学中,机密性可以通过加密来取得[15]。 数字签名提供完整性、认证和不可否认性。 如果我们需要同时取得机密性、完整性、认证和不可否认性,一个传统的方法是先对消息进行签名,然后再进行加密,称为“先签名后加密”方法。 这种方法的计算量和通信成本是加密和签名代价之和,效率较低。1997 年,Zheng[16]提出了一种新的密码原语来同时取得这四种安全性质,他称这一密码原语为数字签密。 签密作为数字签名在密码系统的重要实践,值得学生进行较为细致的学习。
在教学中,我们先通过比较签密和传统方法的区别来进一步了解签密。
比起传统的“先签名后加密”,签密具有以下优点:签密在计算量和通信成本上都要低于传统的“先签名后加密”方法;签密允许并行计算一些昂贵的密码操作;合理设计的签密方案可以取得更高的安全水平;签密可以简化同时需要保密和认证的密码协议的设计。
(1)基于PKI 和身份的签密体制的渐进式教学
在了解签密的基础知识后,我们通过学习签密的体制来进一步深入了解签密的分类。 在教学中,我们以基于PKI 的签密体制和基于身份的签密体制为例。 我们通过表9 进行教学。

表9 基于PKI 和身份的签密体制的渐进式对比
在完成基于PKI 的签密体制和基于身份的签密体制的学习后,我们通过比较签密体制在系统参数、密钥生成、签密、解签密等方面来渐进学习基于无证书的签密体制以及未来可能出现的后量子的新型签密体制。
完成签密体制的学习后,我们应进行具体的签密的方案学习,在基于PKI 的签密体制的学习中,我们以Zheng 提出的两种方案为例。
(2)SCS1 和SCS2 的渐进式教学
Zheng[16]提出了两个相似的签密方案,称为SCS1 和SCS2。 在教学中,我们通过表10 进行教学。

表10 SCS1 和SCS2 的渐进式对比
在基于身份的签密体制的学习中,我们通过学习方案在签密、解签密的效率和安全属性等方面,来具体学习这些基于身份的签密方案。 其中nu和nm分别表示身份和消息的比特长度。
签密的效率和安全属性对于评判签密设计的好坏具有重要意义,在进行签密教学时,我们通过分析算法在签密和解签密中对运算以及点成运算的数量来判断签密的效率;在安全属性的学习时,通过全方位属性的对比,从而渐进了解签密算法的安全情况。
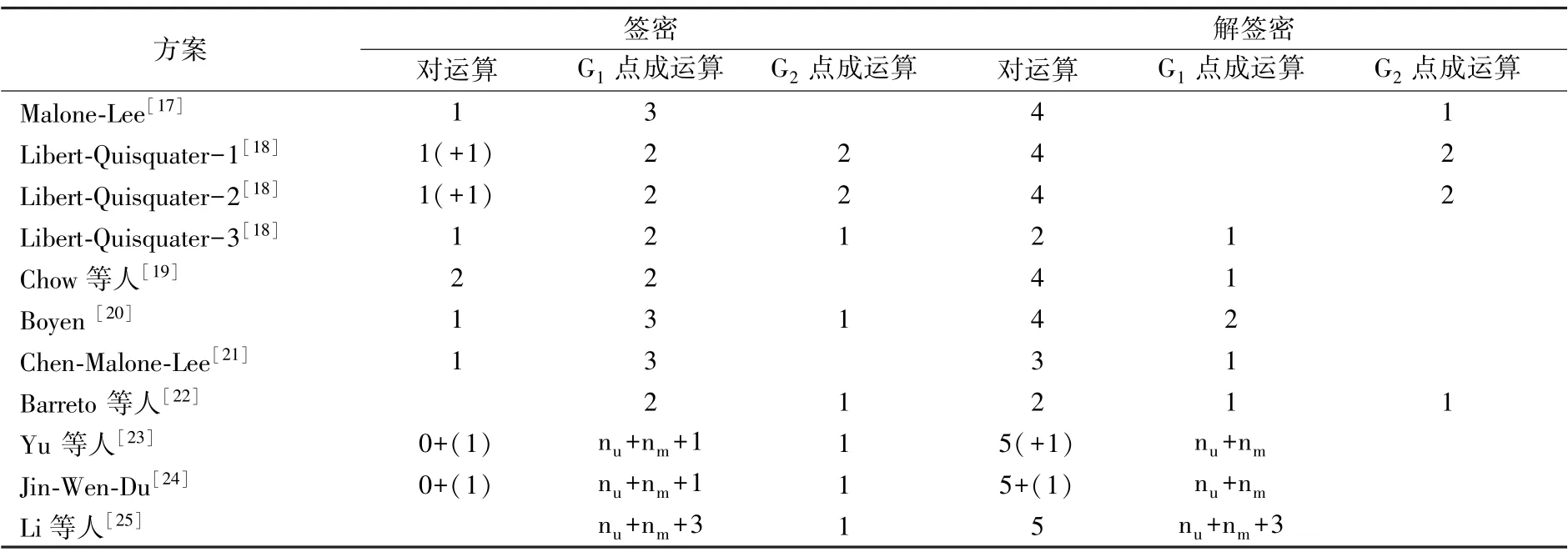
表11 基于身份的签密体制的效率对比
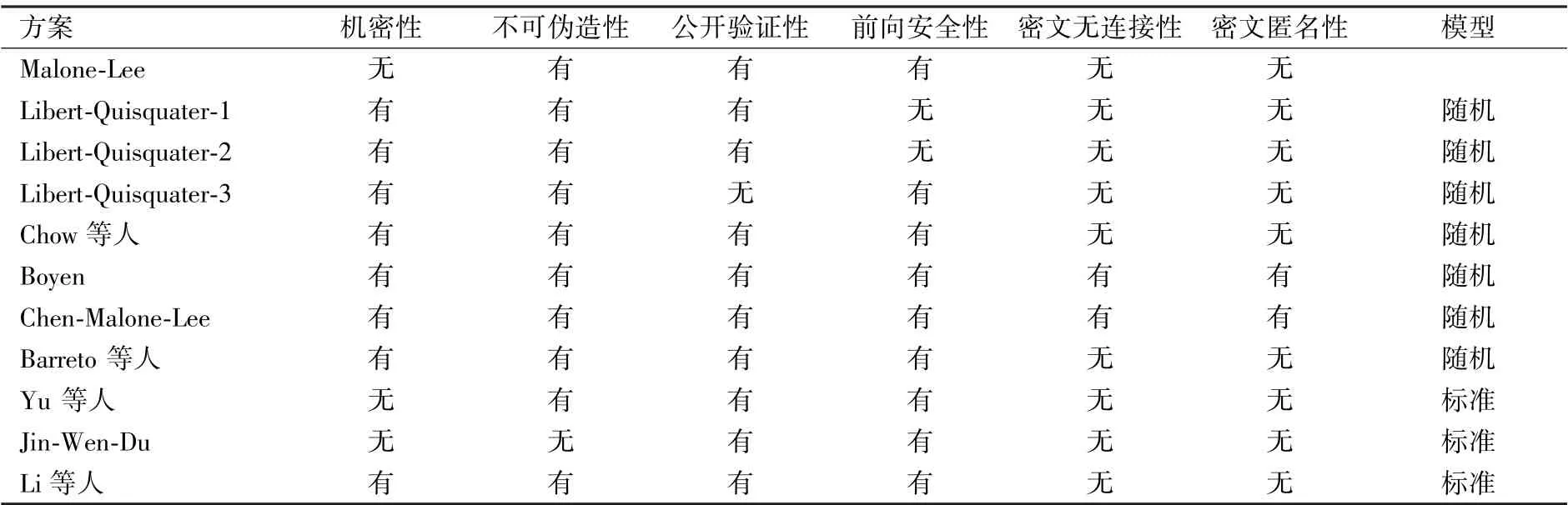
表12 基于身份的签密体制的安全属性对比
在进行签密的教学时,我们首先学习签密体制,其次学习签密的具体方案,然后进行签密方案效率分析的学习,最后学习签密的安全属性分析。 在学习过程中不断通过对比分析表格中相关数据来渐进学习签密,这为学生学习签密提供了一种较为立体的思路,为学生未来从事相关研究做好基础知识的准备。
5.2 典型身份识别方案的渐进式实践教学
零知识身份证明在密码学中占有着十分重要的地位,同时也作为身份认证在实际过程中重要实践。
零知识交互式证明是由Goldwasser、Micali和Rackoff 提出的[26]。 零知识证明是指示证者P 在不向验证者V 提供任何有用的信息的情况下,向验证者V 证明某个论断的方法。 另外,零知识证明还具备有“零知识性”。 即验证者在相信示证者的同时,无法获得有关被证明论断的任何知识。
在教学中,我们以Feige-Fiat-Shamir 体制Guillou-Quisquater 体制和Schnorr 体制为例。
在教学过程中,我们首先学习F-F-S 体制,对该体制我们进行较为详细的教学;其次学习GQ 体制,通过分析对比上述表格中和F-F-S 体制的区别进行学习,最后通过分析和前两种体制的不同来渐进学习Schnorr 体制。 虽然教学难度逐步递升,但在前面教学的基础上进行学习可以帮助同学们更好、更快地掌握后续较为复杂的知识。 未来我们学习新颖的零知识证明的身份识别体制也可以通过分析比较上述因素来学习。
5.3 基于数字签名的认证协议的渐进式实践教学
基于数字签名的认证协议已经在密码系统的实践中被广泛应用,在教学中我们以基于El-Gamal 的认证协议为例。

表13 三个零知识证明的身份识别的渐进式对比
教学过程中,我们首先学习基于ElGamal 的认证协议,对该认证协议我们进行较为详细的教学;其次学习改进协议,通过分析两者在系统参数、用户注册和用户认证的相同不同来渐进学习,然后再学习影响协议计算量的具体因素。 未来我们学习其他的基于数字签名的认证协议也可以通过分析比较上述因素来学习。
6 课程教学中的教学实践经验
通过总结分析渐进式理念的的课程教学,大量的课程教学实践表明在进行渐进式教学的过程中,我们应注意以下几方面:
(1)知识区分
本课程所包含的知识量大,对教学内容应进行合理有序的区分,将数字签名和认证技术的教学内容从大方面分为理论、应用以及实践三个层次,从宏观上为学生树立一个知识体系的大框架。
在理论上,主要讲授数字签名的基础算法标准以及认证协议的经典案例;在应用上主要介绍签名算法和认证协议在应用方面的拓展知识;在实践方面的教学中,主要讲解签名和认证协议在密码系统等领域的具体实践。 其次针对各个部分知识的难度以及关联特点,再继续细分为一个个对比案例,做好教学内容在微观层面的区分工作,将课程的知识体系建立的更加丰富、条理、清晰。
(2)知识联系
在进行教学时,教师应选择一个切入点进行教学,由浅入深,循序渐进,将教授的知识前后联系起来,通过前面简单知识的铺垫,将后续复杂的知识讲的通俗易懂,从而提高教学的有效性。

表14 基于ElGamal 的认证协议及其改进协议的渐进式对比
在选择具体案例时应从简至难,找到案例共同点和不同点,条理清晰地为学生展现出知识的具体联系,做好知识之间的纽带工作。 理清教学内容的联系有助于学生准确理解数字签名和认证技术的概念, 了解各部分之间的联系, 便于学生掌握和记忆。 本课程是在《密码学》课程基础上,对数字签名和认证这一部分内容进行全面、深入的讲解。 在教学过程中可以对之前所学密码学的知识进行巩固,同时做好知识的拓展以及延伸。
(3)内在关系
从签名算法到签名标准,从基础协议到改进协议,从一般方案到推广方案,每个案例的选取都应该考虑到案例之间的内在关系。
通过将案例渐进式地讲给学生,不仅使之懂得基础算法协议的知识,更能快速掌握复杂改进算法协议的精髓。 在进行教学时,教师应做到理论与应用实践相衔接,让学生在学习过程中逐步建立起立体的知识体系,让学生不仅能快速把握知识点的内在联系,更能掌握发现知识内在关系的能力,养成一种良好的学习习惯,为未来继续深入学习提供一种学习方法和思路。
(4)突出层次
渐进式教学是一个层次分明的过程,在教学时要做到根据层次实际,精心设计教学,教师应为学生理清每个部分的教学内容,做到从简到难,前面教学的一步步铺垫都是为了引出最后较为困难、复杂、新颖的知识点,清晰的层次是为了引导学生形成学习签名算法和认证技术的准确逻辑,从而缓解畏难情绪和提高学习兴趣。
教学中过多案例也会使教学进度放缓, 所以应注意每个层次的案例选择是否适量、典型。同时还应充分利用图片、表格等直观明了的方式, 提高教学效率和效果。
7 总结
数字签名和认证技术作为密码学的主要分支之一,在众多信息安全领域得到了应用,其重要作用也日益显现。 本课程是《密码学》专业基础课的必要延伸,是信息安全类课程所用认证技术的更为全面和深入的介绍。 提高学生对于课程的学习兴趣,培养学生密码技术的综合素养是教学中的重要任务。 本文提供了数字签名和认证技术课程的渐进式教学案例设计,旨在学生以更加生动形象的方式,了解和学习数字签名以及认证技术在算法、应用以及实践的知识同时对教学实践经验进行总结。 进行案例化教学时,要注意对比案例的选取,从简至难,找到案例共同点和不同点,以生动活泼的案例对比,使学生形成系统的密码学背景知识体系,开阔眼界,提高专业素质,为今后的课程学习和实践打下坚实的基础,这对于学生从事密码与信息安全类工作和研究具有重要意义。

