动态罚函数法求解约束优化问题

原杨飞，党乾龙，徐 伟，刘玲玲，罗宇婷

西安电子科技大学 数学与统计学院，西安710126

约束优化问题（constrained optimization problems，COPs）在实际生活中普遍存在，涉及到的领域包括汽车设计[1]、电路设计[2]、生产调度[3]等。不失一般性，一个COP可以表示为：

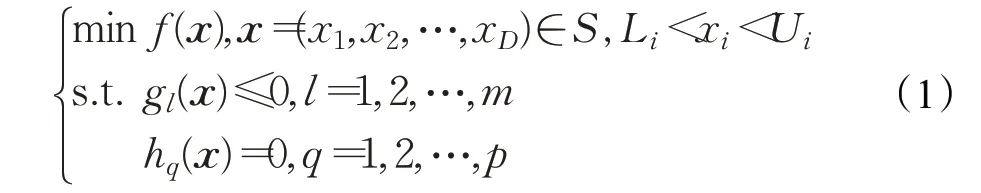
其中，f(x)是目标函数，x是一个D维决策变量，S是决策空间，Li和Ui分别是xi(i=1,2,…,D)的上界和下界，gl(x)和hq(x)分别是第l个不等式约束条件和第q个等式约束条件。在COPs 中，等式约束通常被转化为如下的不等式约束来处理：

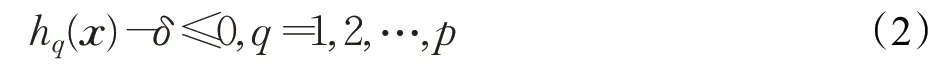
其中，δ是一个很小的正数，决策变量x违反所有约束条件的程度为：

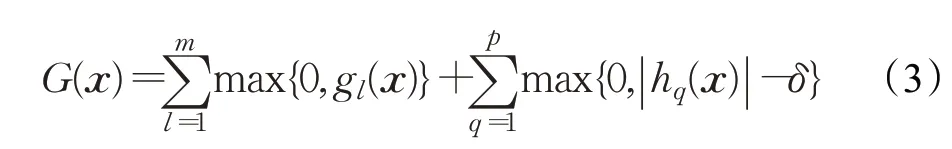
其中G(x)≥0。当G(x)=0 时，称x为可行解。否则，称x为不可行解。

近年来，求解COPs 的算法主要分为传统优化算法和进化算法两类。传统优化算法包括简约梯度法、投影梯度法、序列二次规划法和外点及内点罚函数法等。这些算法在求解时需要利用函数的梯度信息，只适用于可微函数，而且容易陷入局部最优[4]。进化算法是一种基于种群的搜索方法，具有鲁棒性强、搜索效率高、适用范围广等特点，对函数性质要求低，只依赖目标函数值，不需要函数的梯度信息，不易陷入局部最优。因此利用进化算法求解COPs 得到了越来越多研究者的关注[5]，这类算法被称为约束优化进化算法。

约束优化进化算法包括进化算法和约束处理技术两部分。在优化过程中，进化算法的本质是产生子代，而约束处理技术的本质是从候选个体中选择优质个体进入下一代，进而使种群收敛到最优解。图1给出了COPs的一个实例。

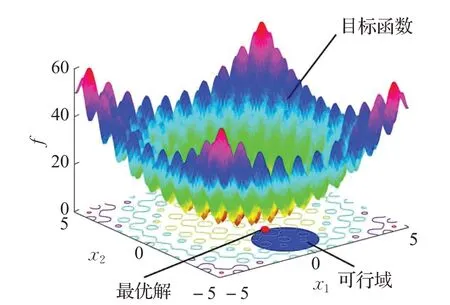
图1 COPs的一个实例Fig.1 An example of COPs

根据约束处理技术的不同，可以将约束优化进化算法大致分为以下五类：罚函数法[6]、可行性准则法[7]、ε约束法[8]、多目标优化法[9]和混合法[10]。罚函数法通过给目标函数f(x)增加一个惩罚项p(x)，将COPs 转化为无约束优化问题进行求解。可行性准则由Deb提出，它基于三条准则比较任意两个个体：（1）一个可行个体和一个不可行个体，选择可行个体。（2）两个都是可行个体，选择目标函数值小的个体。（3）两个都是不可行个体，选择约束违反程度小的个体。ε约束法通过人为设定ε值，将约束违反程度小于ε的个体视为可行个体进行比较，通过这种方式，部分不可行个体被选择进入下一代，有利于增加种群的多样性。多目标优化法将COPs转化为多目标优化问题，然后利用多目标优化技术求解转化后的优化问题。混合法将几种约束处理技术组合起来求解COPs。

约束优化进化算法的核心是如何有效平衡种群的目标函数和约束违反程度，为了实现这个目的，本文提出一种基于动态罚函数的差分进化算法求解COPs（differential evolution algorithm based on dynamic penalty function to solve COPs，PECO）。对IEEE CEC 2010 和IEEE CEC 2017 两组基准测试集进行数值实验，结果表明PECO在大多数测试函数上性能优于其他比较算法。

1 ε 约束法

ε约束法是Takahama和Sakai提出的一种具有代表性的约束处理技术，对于任意两个个体xi和xj，满足以下任一条件，xi优于xj：

其中，

这里，ε0是初始阈值，t和T分别是种群的当前迭代次数和最大迭代次数，λ和p是两个参数，ε随迭代次数的增加而减小。

2 差分进化算法

1997年Storn和Price提出差分进化算法（differential evolution，DE）[11]，其具有结构简单、易于实施、鲁棒性好、收敛速度快等优点。该算法包含初始化、变异、交叉、选择四个步骤。

初始化：在决策空间S中随机产生一个初始种群，其中m表示种群大小。

变异：对每个目标向量，利用变异算子产生一个变异向量。常用的变异算子如下：

其中，F是缩放因子。是种群中随机选择的三个不同的个体。是种群中最好（罚适应度值最小）的个体。

交叉：目标向量和变异向量采用二项式[12]交叉产生试验向量。

选择：根据个体的目标向量和试验向量的适应度值挑选好的个体进入下一代。

3 动态罚函数法求解约束优化问题

3.1 研究动机

罚函数法是处理约束的一种简单有效的方法，但罚系数值在很大程度上依赖于所优化的问题，难以选取。为了解决这个问题，提出动态罚系数策略，其中罚系数根据种群的可行解比例和进化代数动态变化。在进化初期采用较小的惩罚系数，有利于种群的勘探。在进化后期或当种群的可行解比例大于设定的阈值时采用较大的惩罚系数，有利于种群的开采和收敛。通过这种方式，可以平衡种群的勘探能力和开采能力。DE 在求解COPs时具有优化效率高、鲁棒性强、收敛速度快等优点，因此使用DE作为搜索算法。为了平衡种群的收敛性与多样性，本文在经典DE算法的基础上，结合两种DE变异策略更新种群。

3.2 搜索算法

本文采用两种DE 变异策略产生试验向量，第一种是DE/current-to-rand/1 变异策略，第二种是DE/rand-tobest/1/bin变异策略，其方程分别为：

其中，Cr表示交叉概率。randj是(0,1)中随机产生的一个实数。jrand是集合{1,2,…,D}中随机选择的一个整数。

式（7）中，当前个体使用种群中随机选择的个体的信息指导搜索，有利于增加种群的多样性，防止种群陷入局部最优。式（8）中，使用种群中最好的个体的信息指导搜索，有利于引导种群向精英解靠近，进而加快种群的收敛速度。在本文中，以相同的概率使用这两个变异策略，通过这种方式，有效平衡了种群在搜索过程中的多样性和收敛性。

3.3 罚系数调整策略

罚函数法在求解COPs 时，首先COPs 被转化为如下的无约束优化问题：

其中ξ是罚系数。在COPs 中，罚系数的设置对于平衡种群的目标函数和约束违反程度是至关重要的。罚系数过大，种群将以较快的速度进入可行域，忽略了对不可行域的勘探，可能会使种群陷入局部最优。罚系数过小，算法对不可行个体的惩罚力度不足，可能会阻碍种群进入可行域。因此，选取一个恰当的罚系数对于求解COPs是非常关键的。本文结合ε约束法提出一种简单有效的罚系数调整策略，其伪代码如算法1所示。其中Pf是种群中可行个体所占的比例。

算法1罚系数调整策略

由算法1 可知，进化初期，种群中的个体大多数为不可行个体，此时罚系数ξ被设置为一个较小的值，例如ξ=1。在这种情况下，个体的目标函数和约束违反程度发挥着同等重要的作用，一些有着较好目标函数值或较小约束违反度的不可行个体有机会被选择进入下一代。这种方式有利于增加种群的多样性和促进种群对不可行域的勘探。随着进化的进行，种群中的部分不可行个体变为可行个体，当种群的可解比例Pf大于设定的阈值时，罚系数被设置为一个较大的值。此时，种群中的不可行个体被给予充足的惩罚，有利于种群快速地收敛到可行域。当Pf接近于1时，适当减小罚系数，有利于种群对可行域边界的勘探。如图2所示，此时种群可以从可行域和不可行域两个方向收敛到最优解。此外，对于具有较小可行域或者约束条件比较复杂的优化问题，种群可能总是处于不可行域中，为了避免种群滞留在不可行域中，ε约束法被采用。当种群中个体约束违反程度的最小值大于所设的ε值时，罚系数被设置为一个较大的值，有利于种群快速地进入可行域。

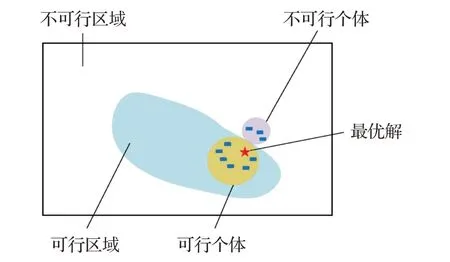
图2 种群搜索最优解的运动轨迹Fig.2 Illustration of population search for optimal solution

3.4 PECO

在求解COPs 时，PECO 首先根据式（9）将COPs 转化为无约束优化问题。接下来，为了平衡种群的目标函数和约束违反程度，根据种群的质量和进化的代数动态地调整罚系数。在优化过程中，结合两个DE 变异策略产生子代。PECO的伪代码如算法2所示。

算法2PECO

4 仿真实验

4.1 演示搜索行为

在本节中，选取如下的三个二维人工测试问题[13]演示PECO的收敛过程：

图3 给出了ATF1、ATF2 和ATF3 的搜索空间、目标函数的等高线图、可行域和最优解。其中ATF1 的最优解位于可行域的内部，ATF2和ATF3的最优解位于可行域的边界上，这里ATF3包含一个等式约束条件。

图3 ATF1、ATF2和ATF3的搜索空间、目标函数的等高线图、可行域和最优解Fig.3 Feasible region，search space，contours of objective function，and optimal solution of ATF1，ATF2 and ATF3

从图4 中可以得到，当最优解在可行域内时（比如ATF1），PECO 可以从不同的方向进入可行域。当最优解在可行域的边界上时（比如ATF2），PECO可以从可行域和不可行域两个方向收敛到最优解。对于ATF3（包含一个等式约束条件），PECO 可以从可行域的两端搜索到最优解。综上所述，PECO有能力求解以上三种不同类型的COPs。

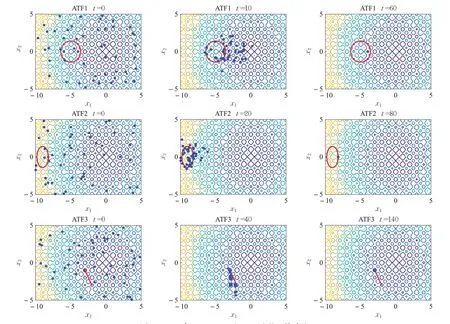
图4 PECO在ATF1、ATF2和ATF3上的收敛过程Fig.4 Evolution process of PECO on ATF1，ATF2 and ATF3

4.2 标准测试函数和参数设置

采用IEEE CEC 2010[14]和IEEE CEC 2017[15]两组基准测试集验证PECO 的寻优性能。IEEE CEC 2010测试集包含18 个测试函数，IEEE CEC 2017 测试集包含28 个测试函数，这两组测试集包含多种不同类型的约束优化问题，例如具有较强的非线性、较小的可行域和旋转不变性等特点。表1给出了测试函数的种群规模(m)、决策变量的维度(D)和最大函数评价次数(maxFES)。在PECO 中，每个测试函数独立运行25 次，涉及到的参数设置如下：p=0.85,λ=10,Gmin=minG(xi),i=1,2,…,m,ε0为初始种群中最大的约束违反值。

表1 测试函数的参数设置Table 1 Parameter settings of test functions

4.3 参数敏感度分析

算法1中，在进化初期，t/T>α时，设置罚系数为一个较小的值。本节针对α的5 种不同取值0.30，0.35，0.40，0.42和0.45，分别进行25次独立实验，讨论α的参数效应。图5 展示了IEEE CEC 2010 基准测试函数C10、C14 和C15，在D=30 时的函数收敛曲线。从图5中可知，C10 在α=0.42 时结果最优，C14 在α=0.42 和0.45 时结果最优，C15 在α=0.40 和0.45 时结果差别不大，找到的解最优。

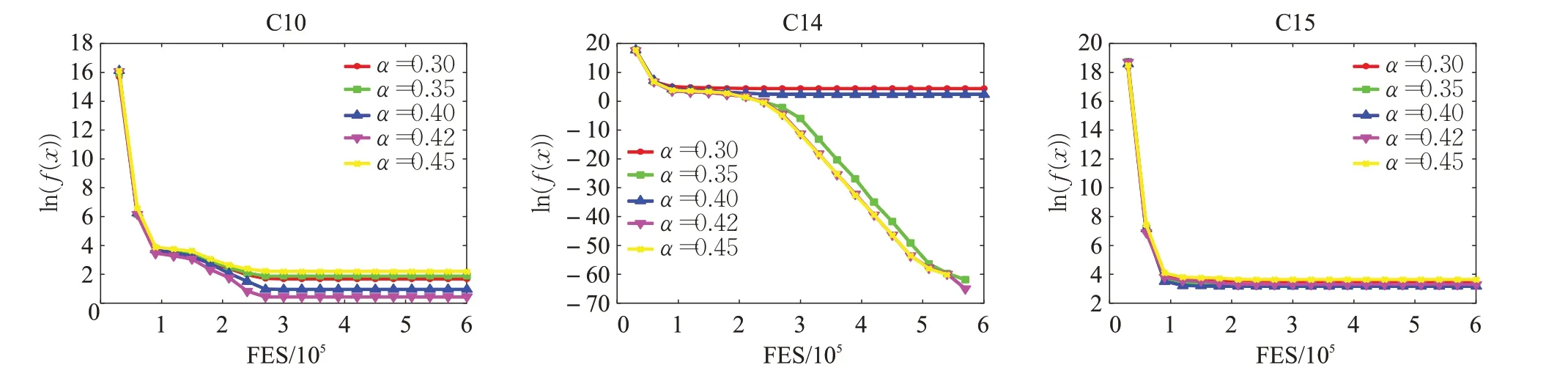
图5 不同α 值的函数收敛性能比较Fig.5 Convergence performance comparison of functions with different α values

在进化后期，当种群的可行解比例Pf >β时，设置罚系数为一个较大的值。这里针对β的5 种不同取值0.5，0.6，0.7，0.8 和0.9，讨论β的参数效应，实验结果在图6 中给出。从图6 中可以得出，C10 在β=0.8 时结果最优，C14在β=0.8 和0.9时结果差别不大，找到的解最优，C15 在β=0.8 和0.9 时结果最优。综上所述，在PECO中，α=0.42,β=0.8。

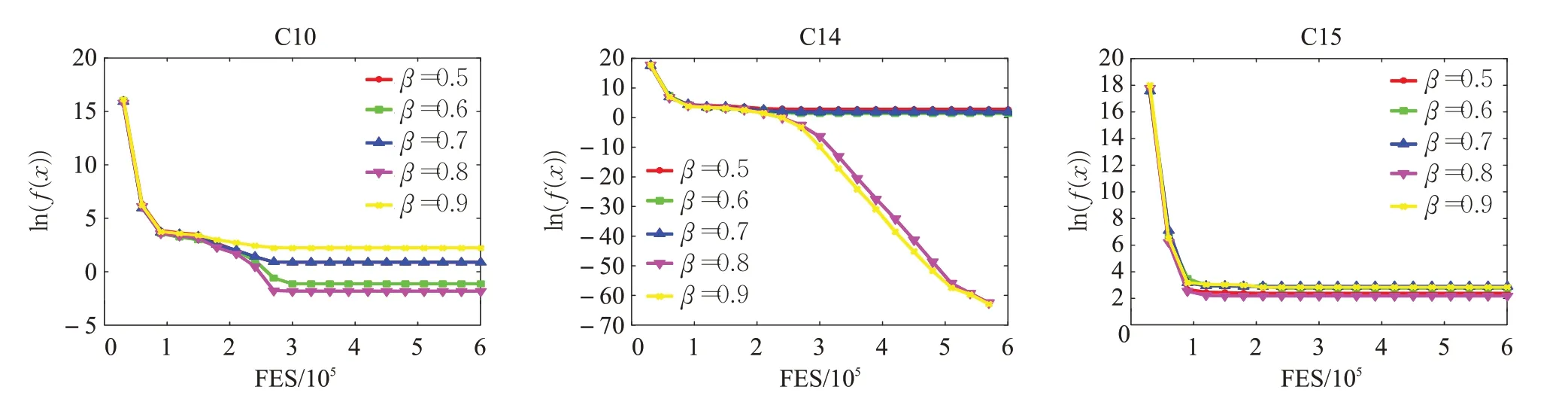
图6 不同β 值的函数收敛性能比较Fig.6 Convergence performance comparison of functions with different β values

4.4 结果对比与分析

为了验证PECO的寻优性能，使用实验中获得的最小可行目标函数值的平均值（Mean）和标准偏差（std）作为评价指标。在IEEE CEC 2010这组测试集中，将PECO与Co-CLPSO[16]、ITLBO[17]、DeCODE[18]、AIS-IRP[19]这4个算法进行性能比较，实验结果在表2中给出。所有对比算法的实验结果均来源于原论文。“∇”表示算法在25次运行中不能找到任何可行解。“+”“-”和“≈”分别表示PECO 在统计性能上优于、劣于和相似于对比算法。从表2中可以得出，D=10 时，PECO分别在12个、6个、6个和11个测试函数上优于Co-CLPSO、ITLBO、DeCODE和AIS-IRP。与PECO相比，Co-CLPSO、ITLBO、DeCODE和AISIRP分别在3个、3个、3个和4个测试函数上占优。D=30 时，PECO分别在17个、11个、6个和15个测试函数上优于Co-CLPSO、ITLBO、DeCODE 和AISIRP。而Co-CLPSO、ITLBO、DeCODE和AIS-IRP分别在1个、4个、4个和2个测试函数上优于PECO。此外，与Co-CLPSO、ITLBO 和AIS-IRP 这3 个算法相比，PECO 在高维测试函数上可以获得更好的性能。

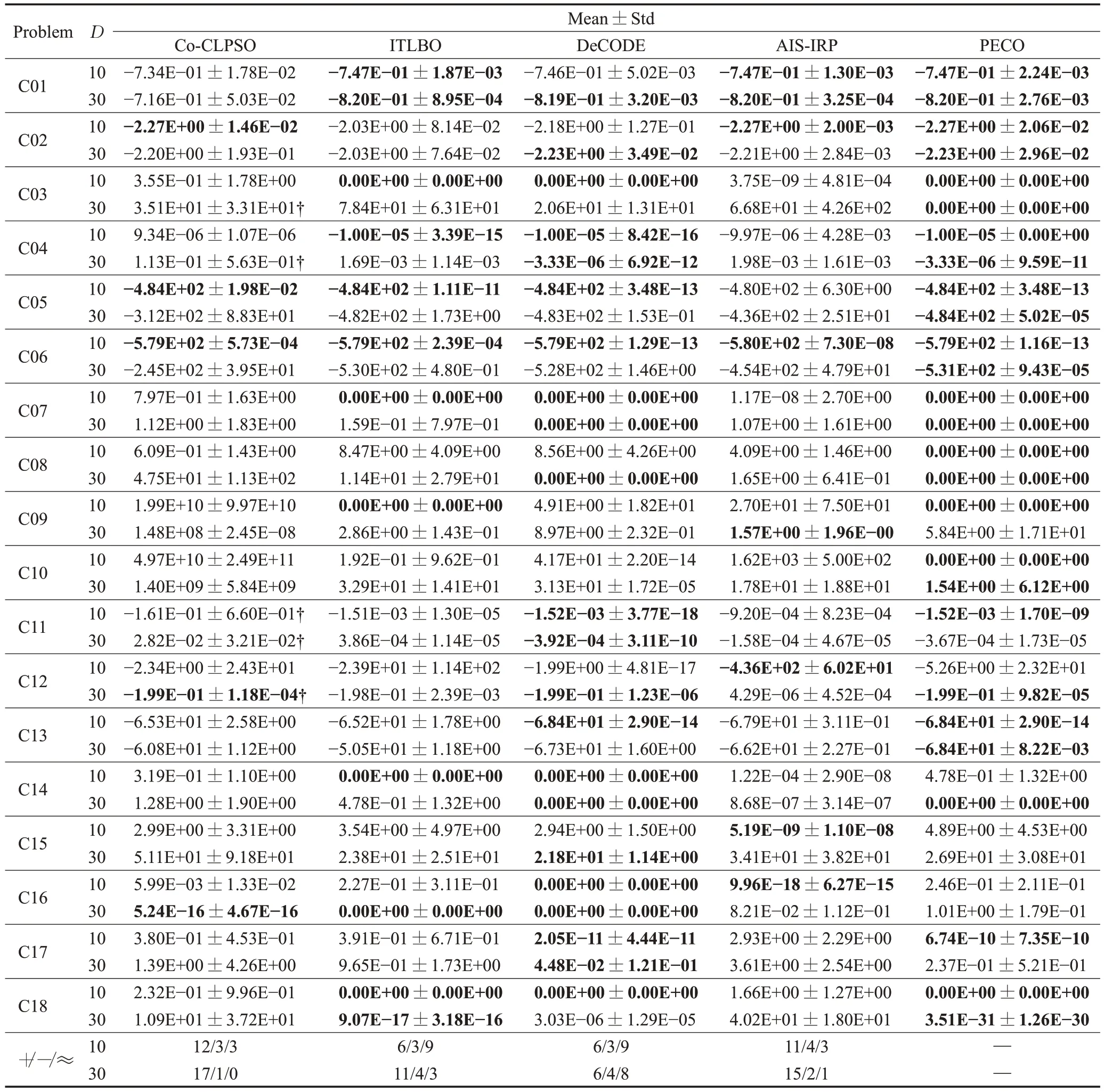
表2 IEEE CEC 2010中18个基准测试函数的实验结果Table 2 Experimental results of 18 benchmark functions in IEEE CEC 2010

在IEEE CEC 2017 这组测试集中，将PECO 算法与MA_ES[20]、IUDE[21]、LSHADE44[22]、UDE[23]这4 个算法进行性能比较，实验结果在表3中给出，其中LSHADE44是IEEE CEC 2017 竞赛中性能最好的算法。在C17、C19、C26、C28 这4 个测试函数上，PECO 与对比算法均不能找到任何可行解，因此不提供它们的实验结果。从表3中可以得出，D=10 时，PECO分别在12个、6个、10个和15个测试函数上优于MA_ES、IUDE、LSHADE44和UDE。与PECO相比，MA_ES、IUDE和LSHADE44分别在3个、2个和3个测试函数上占优，同时，UDE不能在任何测试函数上优于PECO。D=30 时，PECO 分别在10个、13 个、14 个和17 个测试函数上优于MA_ES、IUDE、LSHADE44 和UDE。而MA_ES、IUDE、LSHADE44 和UDE分别在4个、4个、3个和1个测试函数上优于PECO。通过上述分析，PECO在整体性能上优于其他对比算法。

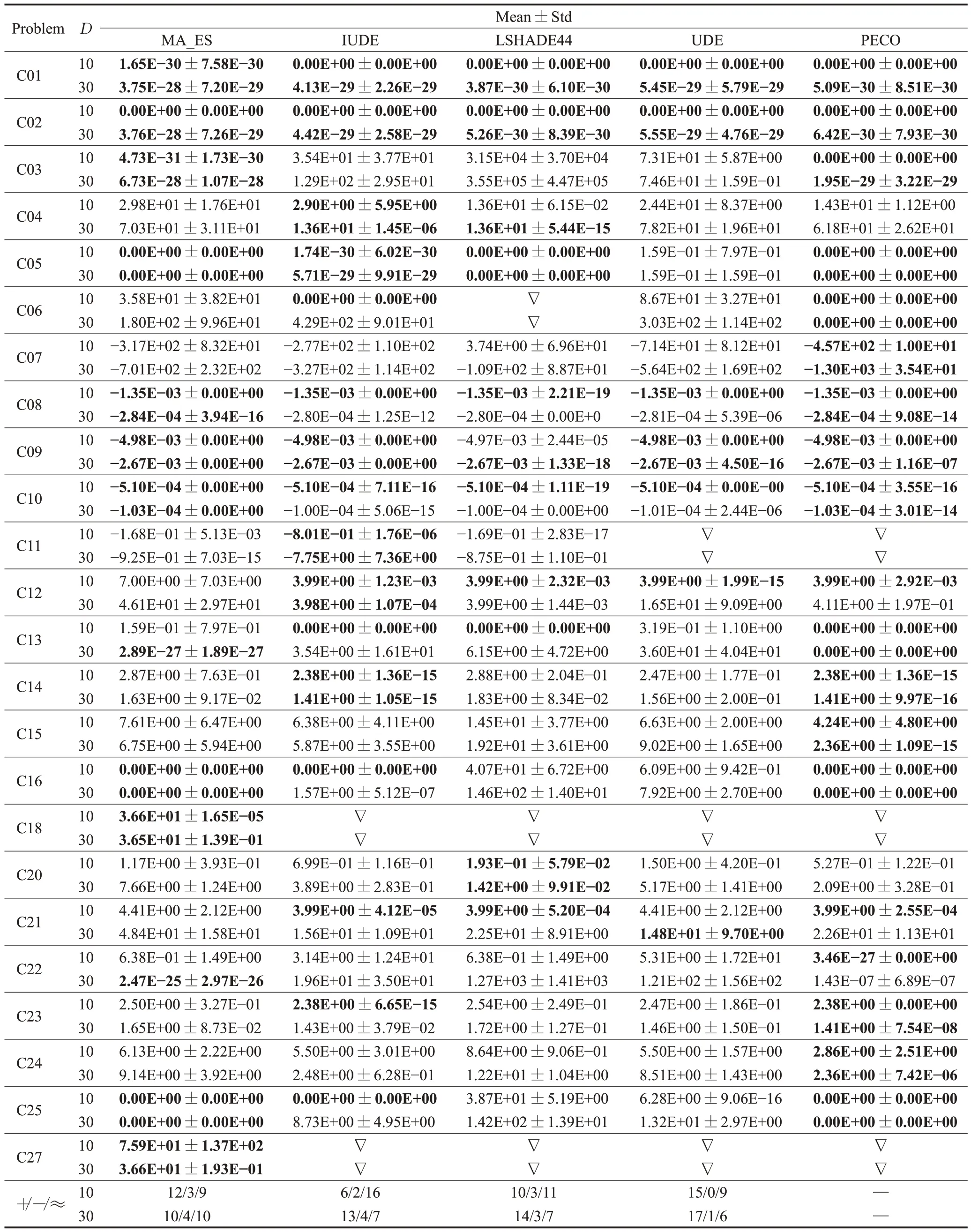
表3 IEEE CEC 2017中28个基准测试函数的实验结果Table 3 Experimental results of 18 benchmark functions in IEEE CEC 2017

5 结束语

本文提出了一种基于动态罚函数的差分进化算法求解约束优化问题。在所提出的算法中，设计了一种与ε约束法相结合的罚系数调整策略，通过这种方式，可以有效平衡种群的目标函数和约束违反程度。此外，为了平衡种群的多样性与收敛性，结合两种DE 变异策略产生子代。实验结果表明，PECO与对比算法相比具有更好的优化性能。下一步将设计一个自适应的罚系数调整策略提高PECO的寻优性能。