分级加载下加筋边坡离心模型试验数值模拟

杨秀杰，邓凯伦，佘孟飞，刘 宏

(1.贵州大学 国土资源部喀斯特环境与地质灾害重点实验室，贵阳 550025；2.中国五冶集团有限公司 天津分公司，天津 300171)

1 研究背景

土工格栅由于其性质稳定、抗拉变形模量大、与土颗粒咬合较好、造价低廉、施工简便等特点被广泛应用于岩土领域[1]。土工格栅与周围土颗粒之间的摩擦和咬合作用改变了土体内部的应力场，起到限制土体侧向位移、减小不均匀沉降，增强土体整体性能的作用[2]。随着我国西部地区的经济发展，西部山区的基础设施迅速发展，不可避免深挖高填，加筋边坡具有沉降小、坡度大、节约占地面积的特点[3]。由于筋土界面及工程实践的复杂性，加筋机理的研究虽取得了一定进展，但其真正工作机理尚未完全清楚，目前的规范设计指南过于保守，无法满足工程实践的需求[4]。

近年来，随着加筋土技术广泛应用，国内外学者对加筋边坡进行了大量研究，已有研究表明，加筋边坡应力应变分布与填料性质、筋材强度、加筋间距、加筋设计、坡度、坡高等因素有关[5-8]。对于加筋边坡离心模型试验及其数值模拟的相关研究，Mehdipour等[9]研究认为边坡中下部筋材拉力最大；陈建峰等[10]研究表明加筋沉降明显减小，而加2层筋效果接近加1层筋。李波等[11]认为在1/6～1/3坡高处出现应力集中。

上述的数值模拟方法基本都是采用M-C(Mohr-Coulomb)模型，此模型在计算过程中很难考虑时间因素，然而离心模型试验的分级加载过程与时间密切相关，关于离心模型尺寸的数值模拟中引入时间因素的相关研究目前尚未多见。

本文采用考虑时间因素的Cvisc蠕变模型对加筋边坡离心模型试验进行数值模拟，同时也采用M-C模型的模拟结果与离心试验结果进行对比分析。采用Cvisc蠕变模型进一步研究不同筋材长度、不同部位筋材加密或筋材模量增加对加筋边坡变形和稳定性的影响。

2 离心模型试验数值模拟

2.1 本构模型的选用

很多学者对分级加载的加筋边坡离心模型试验的数值模拟采用M-C模型，该模型在计算过程中没有时间参数。分级加载的离心模型试验其离心加速度是随时间变化的，在对其进行数值模拟时，通常是设置一级重力加速度后，将离心模型计算到一定的最大不平衡力与典型内力的比率，或计算一定的步数[12-13]，使数值模拟达到与试验结果相应的位移量，再进行下一级加载计算，模型需要计算到多少比率的内力平衡，计算多少步数，都没有统一的标准，模拟的难度较大。因此考虑变加速度加载时有必要选用具有时间因子的本构模型，本文采用的本构模型是FLAC3D蠕变模块中的Cvisc蠕变模型，同时也采用M-C模型进行相应的模拟，并与离心模型试验结果进行对比。

2.2 蠕变本构模型

本文采用的是Cvisc黏塑性模型，如图1所示，Cvisc黏塑性模型由Burgers(伯格斯)模型(由Maxwell体与Kelvin体串联组成)与M-C模型串联组成，整个模型由5个元件组成，其中弹性元件2个，粘性元件2个，塑性元件1个。EM和EK分别为Maxwell体弹性模量和Kelvin体弹性模量，ηM和ηK分别为Maxwell体黏性系数和Kelvin体黏性系数，σt表示服从M-C强度准则的岩体屈服强度。εM、εK、εP分别为Maxwell模型、Kelvin模型和M-C模型中的应变。

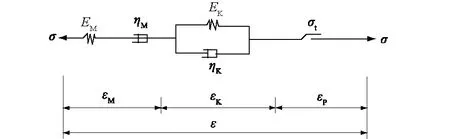
图1 Cvisc蠕变模型示意图Fig.1 Schematic diagram of Cvisc rheologic model

在Burgers模型中如果不考虑Maxwell体中的黏性系数，相当于在Burgers模型中去除一个Maxwell体中的黏壶，此时的Burgers模型退化成Kelvin体串联一个弹簧，转变成广义开尔文模型；Cvisc模型相当于广义开尔文模型与M-C模型相结合的黏弹塑性模型。广义开尔文模型的应变可表示为

(1)

此时的Cvisc模型的本构方程可表示为：

(1)当σ<σt时，有

(2)

(2)当σ≥σt时，有

(3)

2.3 模型对象

离心模型试验的原型为西南地区某机场加筋边坡，最大填方高约 50 m，离心模型最大填方高度为38.5 cm，模型率N=130。原型边坡坡比为1∶1，本文研究的离心模型坡比为1∶0.5。在离心模型中埋设9个土压力传感器，在筋材表面用环氧树脂粘贴了19个应变片。在试验过程中，有些仪器读数异常或损坏，离心模型中的土压力计和应变片的布置如图2所示，图中仅为读数正常的仪器。

图2 离心模型监测点布置示意图Fig.2 Layout of monitoring of centrifuge model

离心试验是通过施加离心加速度来实现模型自重的增加，从而使得模型的变形和破坏模式与原型相似。根据离心模型的相似关系[14-16]，土工格栅的厚度按照相似比例缩尺130倍在一般的加工技术下几乎很难实现，所以选取的替代加筋材料其抗拉强度应是原型土工格栅的1/130。在现场填筑过程中，格栅分层厚度为0.5 m。如果按相似比计算，则离心模型中每层厚度仅3.8 mm，在模型制备上无法实现，本次试验模型中筋材层厚度取2.3 cm，相当于筋材每层厚度增加6倍，则相应的筋材强度应增加6倍。现场共用3种土工格栅，平均抗拉强度为210 kN/m，本试验选取的土工格栅替代材料为耐碱玻璃纤维网，其抗拉强度为9.7 kN/m。

根据离心模型试验与原型的相似关系，仅考虑惯性和重力的影响时，时间比尺为 1/n[17]。采用变加速度方法模加筋边坡的填筑过程，将离心模型逐级提高离心加速度至30g、60g、90g、130g，前3级加载离心机保持运行时间均为5.5 min，模拟边坡填筑施工时间0.5 d，最后一级荷载保持运行时间为44 min，模拟边坡填筑施工完毕后的4 d沉降。离心机运行过程中加载时间-加速度关系曲线如图3所示。

图3 加速度与时间关系曲线Fig.3 Relationship between acceleration and time

2.4 数值模型及材料参数

采用FLAC3D有限差分软件对离心模型试验建立相同尺寸的网格模型，模拟离心模型试验的变加速度加载过程，数值网格模型如图4所示。筋材布置与模型试验相同，模型格栅抗拉强度取值为9.7 kN/m，通过室内拉拔试验得出筋土界面强度折减系数为0.6，即筋土界面参数为填料参数的0.6倍。计算参数见表1—表3。

图4 离心试验数值模型Fig.4 Numerical model of centrifugal test

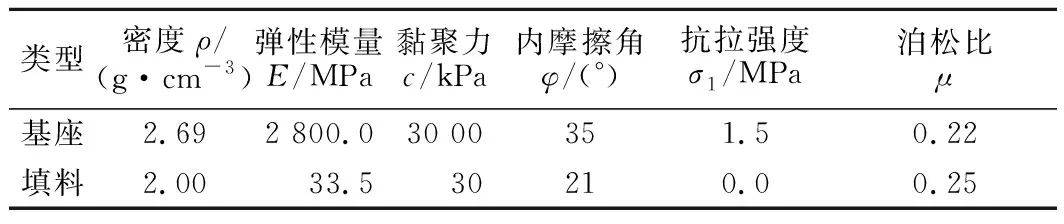
表1 基座和填料参数采用值Table 1 Values of base and filling parameters

表2 蠕变模型参数取值Table 2 Value of creep model parameters

表3 土工格栅的材料参数Table 3 Material parameters of geogrid

2.5 计算过程

图3展示了加速度-时间关系通过命令对数值模型分级施加重力加速度。将重力加速度依次设置为30、60、90、130g。Cvisc模型施加每一级离心加速度后计算相应的时间步。M-C模型采用 FLAC 默认的收敛标准，模型中最大不平衡力与典型内力的比值<10-5时，进入下一级重力加速度计算，直至130g时终止。

3 离心试验和数值模拟结果对比分析

3.1 坡肩沉降

如图5(a)所示，离心模型试验运行结束后，观测到最大竖直沉降发生在坡肩处，在边坡顶面距坡肩16.8 cm处出现了平行于边坡方向的拉裂缝。图5(b)为数值模拟130g时塑性区分布，从图5可以看出，边坡最先发生塑性屈服的是坡脚部位，随后逐渐沿加筋体后缘向上发展，在边坡顶面也形成相应的受拉塑性屈服，仅有边坡中上部完整，未形成连通的潜在滑面。

图5 坡顶拉裂缝及塑性区分布Fig.5 Tensile cracks at slope top and plastic zone distribution

表4为Cvisc模型与M-C模型在不同离心加速度加载时坡肩处沉降结果对比，本次离心模型试验运行结束时坡肩沉降量为6.04 cm，Cvisc模型与M-C模型加载到最终的130g时坡肩沉降与试验结果基本吻合，但M-C模型在重力加速度较小时，沉降量较小。

表4 2种数值模型坡肩沉降对比Table 4 Comparison of settlement at slope shoulder between two numerical models

图6(a)为文献[18]中的加筋边坡离心模型试验实测的沉降与时间的关系；图6(b)为Cvisc模型坡肩处的沉降与时间的关系。从图6可知，重力加速度增加阶段，沉降发展较快；重力加速度稳定阶段，沉降发展缓慢，Cvisc蠕变模型的蠕变起作用(见图6(b))。Cvisc蠕变模型的沉降随时间的发展曲线与文献[18]的实测结果的发展趋势基本一致。

图6 沉降-时间曲线Fig.6 Curves of settlement versus time

3.2 竖向土压力

图7为离心试验与两种模型数值模拟结果的土压力与加速度关系图，由图7可见3条线形基本一致，土压力随着离心加速度的增加而增加。当重力加速度<90g时，两种模型数值模拟的土压力与试验非常吻合；重力加速度为130g时，M-C模型的土压力偏高8%～29%，Cvisc模型偏高2%～17%。

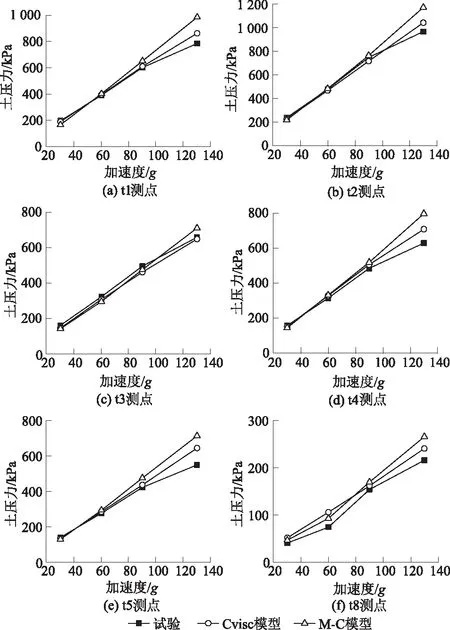
图7 数值模拟与试验土压力比较Fig.7 Comparison of earth pressure between numerical simulation and centrifugal test

图8显示Cvis模型与试验实测土压力随时间的变化曲线，两者的整体变化趋势一致，与离心加速度一样呈阶梯状逐级增加。加速度保持130g稳定后，Cvisc模型土压力基本保持稳定，试验实测土压力稍有降低的趋势，可能是土压力计与填料之间接触松弛。Cvisc模型的土压力与试验测得的土压力吻合较好，可以反映出各个时刻的土压力。

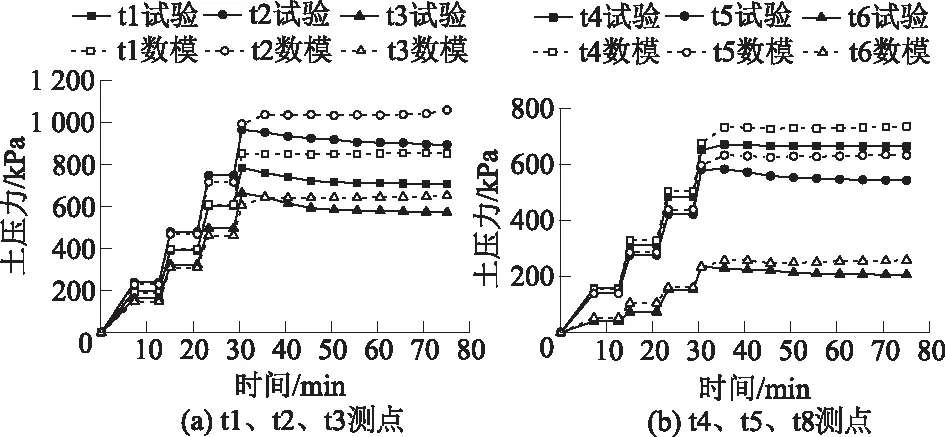
图8 土压力-时间曲线Fig.8 Curves of earth pressure versus time

3.3 筋材拉力

图9为离心试验与两种模型模拟结果筋材拉力与加速度的关系，离心试验中所测的筋材应变，根据公式σ=Eε可得出应力值，用所得出的应力值乘筋材厚度可转换为筋材拉力。由图9可知Cvisc模型筋材拉力与试验实测结果吻合较好，而M-C模型在图中的斜率明显偏大，与试验实测值不太符合。M-C模型筋材拉力偏差较大的原因是：可以从表4中看出，在重力加速度较小时，M-C模型的位移较小，重力加速度增加到130g时，M-C模型的位移又稍大，因此造成加速度较小时，M-C模型筋材拉力较小，当加速度较大时，筋材拉力偏大。

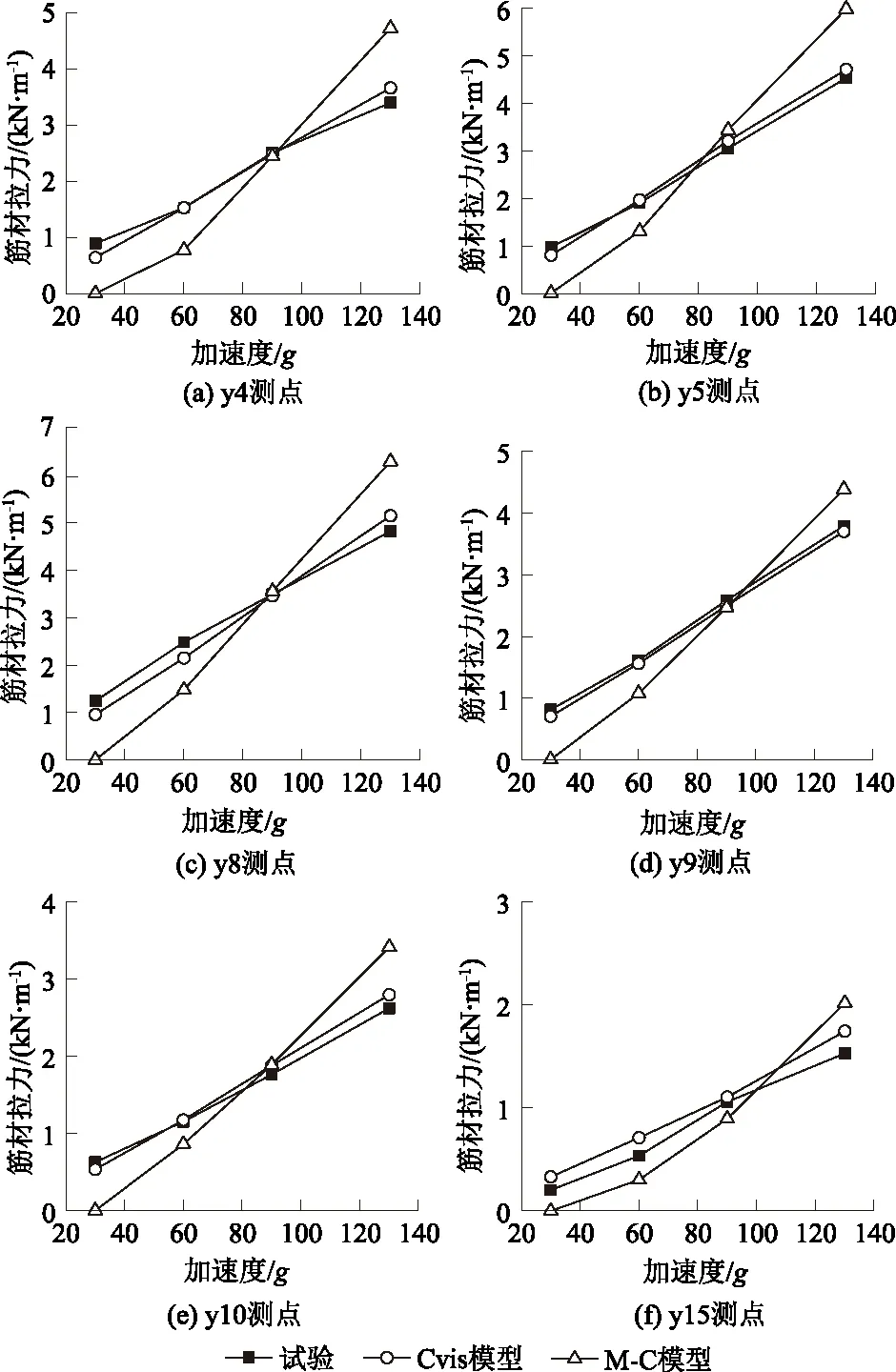
图9 数值模拟与试验加筋拉力比较Fig.9 Comparison of reinforcement tension between numerical simulation and centrifugal test

图10为Cvisc模型与离心试验的筋材拉力与时间关系曲线，由图可知重力加速度较小时，数值模拟结果与试验结果较为吻合；当重力加速度较大时，数值模拟值略高，y4、y5、y8点在130g时数值模拟筋材拉力比试验实测高6%～13%。Cvisc模型的筋材拉力与试验实测结果吻合很好，可以反映出各个时刻的筋材拉力。

图10 筋材拉力-时间关系曲线Fig.10 Curves of tensile forces of reinforcements versus time

图11为Cvisc模型130g时筋材拉力分布，由图可知，数值模拟结果表明在1/3坡高处筋材拉力最大。底部筋材拉力向下逐渐减小，原因是边坡底部的摩擦阻力的作用限制了边坡的位移，由筋土变形协调理论可知筋材拉力向下减小[19-20]。图12为离心试验在坡高1/3处发生侧向鼓出，说明最大水平位移发生在距坡底1/3坡高处，可视作易发生筋材拉断造成边坡失稳的趋势或先兆。

图11 数模筋材拉力分布Fig.11 Distribution of geogrid’s tension in numerical model

图12 离心试验坡面鼓出Fig.12 Bulge of slope in centrifugal test

3.4 两种本构模型的探讨

上述研究表明，对分级加载离心模型试验的数值模拟，M-C模型没有时间因子，只能采用控制计算步数或控制最大不平衡力与典型内力比值的方式，将数值模型计算到每级荷载与模型试验相应的沉降量，至于最大不平衡力与典型内力比值取多少，不好控制，同样采用控制计算步数的方法也比较难。

根据以上情况，有必要采用具有时间因子的本构模型对变加速度加载下的离心模型试验进行数值模拟。而本文采用Cvisc蠕变模型，所得的沉降与时间的关系曲线与文献[18]的离心试验位移结果相似，沉降在加速度增大时沉降发展较快，加速度稳定后沉降发展缓慢。并且Cvisc蠕变模型的土压力与筋材拉力与本试验的非常吻合，能够正确反映离心模型试验任何时刻的应力与应变分布情况，说明本文采用Cvisc蠕变模型模拟变加速度加载的离心模型试验的数值模拟是合适的。

4 数值模拟的拓展研究

数值模型和离心试验结果表明，坡高1/3处筋材拉力值最大，易筋材拉断导致边坡整体失稳。针对离心模型试验，采用Cvisc模型分析离心模型中筋体长度和不同位置的筋材间距、筋材模量等因素对离心模型试验结果的影响。数值模型研究方案如表5所示，筋材的长度、间距、弹性模量是主要的设计参数。

表5 数值模拟研究方案Table 5 Research scheme of numerical simulation

由图13可知，通过增加筋材长度，潜在滑动面随之后移且逐渐变缓。从表6和图14可以看出，筋材长度越长，坡肩沉降量越小，边坡稳定性越高。随着筋材长度的增加，有效加筋范围逐渐增加。筋材长度较短时(15、20 cm)，边坡失稳，穿过滑动面起到加固作用的筋材条数较少，仅为坡脚处1/5坡高范围内的筋材起到加固作用，筋材内力高度集中，但筋材长度较短，与填料的摩擦长度不足，导致筋材最大拉力偏低；筋材较长时(≥25 cm)，穿过潜在滑动面的筋材增多，有效加筋范围有所增加，并且随着筋材与填料的摩擦长度的增加，筋材承受的拉力值也有所提高，限制边坡变形的效果增强，增加了边坡的稳定性。

图14 不同筋材长度的坡肩沉降比较Fig.14 Comparison of settlement at slope shoulder with different lengths of reinforcement

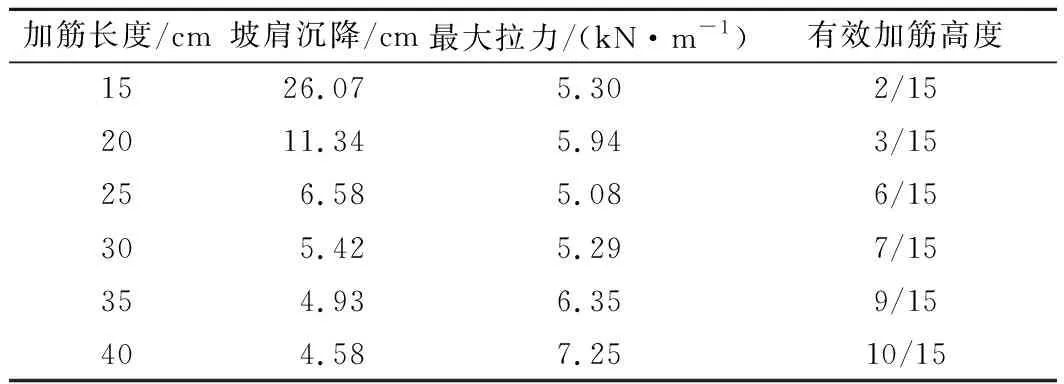
表6 不同加筋长度下边坡情况对比Table 6 Comparison of slope conditions with different grid lengths

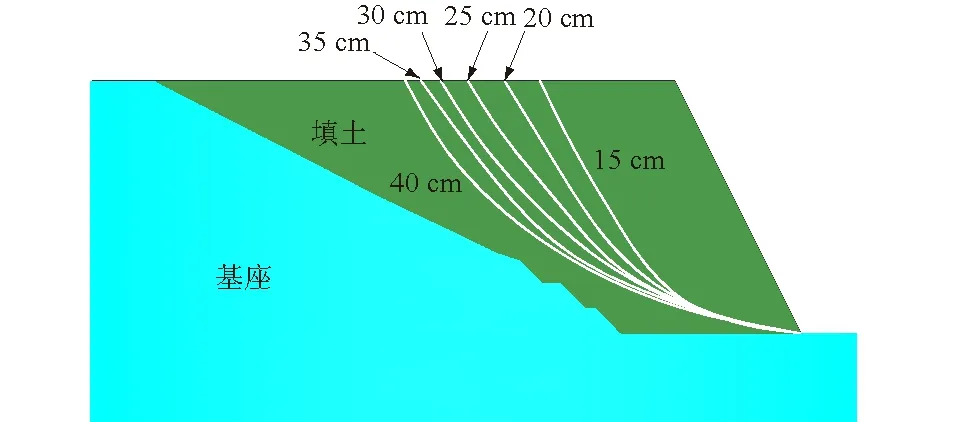
图13 筋材长度与潜在滑动面关系Fig.13 Relationship between reinforcement length and potential sliding surface

由表7和图15可以看出，在1/6～1/2坡高处加筋加密和模量增加起到的加固效果最好，其次是中部和下部，上部效果最差。筋材加密一倍比筋材模量增加一倍起到更好的效果。上部筋材加密一倍，坡肩沉降减小7.5%；中部和下部筋材加密一倍起到的效果相当，两条曲线几乎重合，坡肩沉降分别减小14.2%和15.4%；1/6～1/2坡高处筋材加密一倍，坡肩沉降减小18.1%。上部筋材模量增加一倍，坡肩沉降减小2.5%；中部筋材模量增加一倍，坡肩沉降减小5.2%；下部筋材模量增加一倍，坡肩沉降减小4.3%； 1/6～1/2坡高处筋材模量增加一倍，坡肩沉降减小5.5%。

表7 M3坡肩沉降计算结果Table 7 Calculated settlement of slope shoulder M3

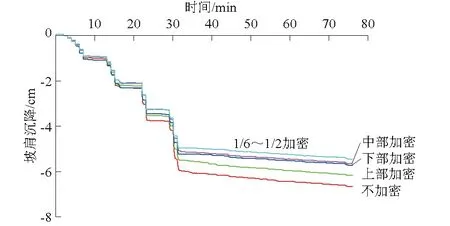
图15 不同部位筋材加密一倍的坡肩沉降比较Fig.15 Comparison of slope shoulder settlement when the grid spacing of different parts is reduced by one time

5 结 论

仅针对西南地区某机场加筋边坡变加速度加载的离心模型试验进行数值模拟，对比了Cvisc蠕变模型与M-C模型的适用性，在未考虑尺寸效应的前提下，采用Cvisc蠕变模型分析了加筋长度，不同部位的筋材间距、筋材模量对边坡位移与应力的影响，得出下面结论：

(1)Cvisc蠕变模型能较好地模拟变加速度加载的加筋边坡离心模型试验的沉降变化特征，土压力与筋材拉力也与试验实测的较为吻合，1/3坡高筋材拉力与水平位移最大也与试验结果一致，说明本文采用的Cvisc蠕变模型可以较好地模拟变加速度加载的加筋边坡离心模型试验。

(2)M-C模型在模拟变加速加载的离心模型试验时，逐级增大重力加速度进行加载模拟时，采用控制计算步数或控制最大不平衡力与典型内力的比值的方法，使每级荷载计算到与试验相应的沉降量，M-C模型在模拟变加速加载的离心模型试验时没有Cvisc蠕变模型简便。

(3)随着加筋长度增加，潜在滑动面随之后移且逐渐变缓，有效加筋范围增加,筋材拉力先增后减再增，边坡变形减小，稳定性提高。以1/3坡高为中心进行筋材加密和筋材模量提高，起到的加固效果最好，1/6～1/2坡高筋材加密一倍后沉降量降低18.1%，筋材弹性模量提高一倍后沉降量降低5.5%，筋材加密一倍比筋材模量提高一倍起到更好的加筋效果。