基于孔隙水分布的非饱和土SWCC及相对渗透系数预测模型
王 欣
(山西工程科技职业大学 工程管理系,太原 030031)
1 研究背景
非饱和土渗透性与暴雨诱发滑坡[1]、高库大坝蓄水[2]等研究领域有着密不可分的联系。然而土体中分布着的孔隙有非常大的复杂性和随机性,使得学者对土体渗流研究的难度变得极大。把土体孔隙简化为一簇毛细管,假设土体孔隙分布服从分形定律可以很大程度地简化其复杂性,可以很明了地研究土体渗流问题,这也正是本文研究的出发点。
由于非饱和土的相对渗透系数测量难度大、费时长,很多学者提出了关于预测非饱和土相对渗透系数的模型[3-11],其中最为著名的是VG模型[6]。VG模型是在提出一个经验性的土水特征曲线模型的基础上,基于Burdine模型[3]和Mualem模型[5]得到了一个封闭的预测相对渗透系数解析表达式。VG模型与试验数据的拟合程度较好,但其解析表达式里参数较多且存在意义不明确的经验参数。Assouline等[12-13]在一种均匀随机破碎过程的土壤结构演化假设概念模型的基础上,提出了一个土水特征曲线概念模型[12]和相对渗透系数预测模型[13]。也有学者[14-17]利用分形理论研究非饱和土渗流问题,他们提出的模型中的参数均具有明确的几何意义或物理意义,但这些研究在局部平衡假设的基础上,认为土体孔隙中对于某一特定孔径r,其中孔径大于r的孔隙被空气填满(干燥状态),孔径小于r的孔隙被水填满(饱和状态),这种假设只考虑饱和孔隙的含水量,忽略了非饱和孔隙(非饱 和状态)的含水量。而实际上土体孔隙水分布存在从干燥状态到饱和状态的逐渐过渡状态,即存在非饱和状态。
本文在前人研究[16-17]的基础上,基于杨-拉普拉斯方程和分形理论对传统的毛细管系统含水量模型进行改进,认为土体孔隙水分布为从干燥状态到饱和状态的逐渐过渡的状态,即认为土体中孔隙水的存在为3种状态:干燥状态、非饱和状态、饱和状态,推导出了土水特征曲线模型和饱和度-相对渗透系数模型。本文提出的土水特征曲线模型包含3个参数,相对渗透系数预测模型只含有一个参数。土水特征曲线模型与饱和度-相对渗透系数模型中的参数均具有明确的几何意义。利用4组试验数据对提出的相对渗透系数预测模型进行验证,用均方根偏差(Root Mean Square Deviation,RMSD)评测试验数据与预测数据之间的误差,结果表明4组数据的均方根偏差(RMSD)均<0.025,说明该模型具有预测非饱和土相对渗透系数的实际意义。
2 模型建立
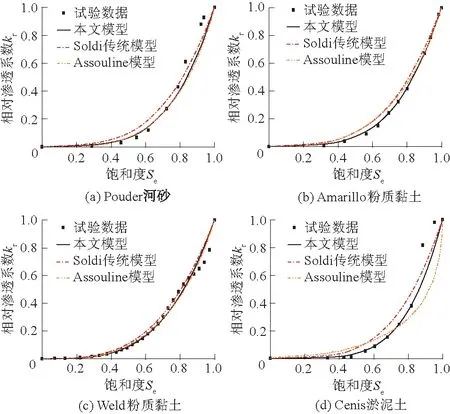
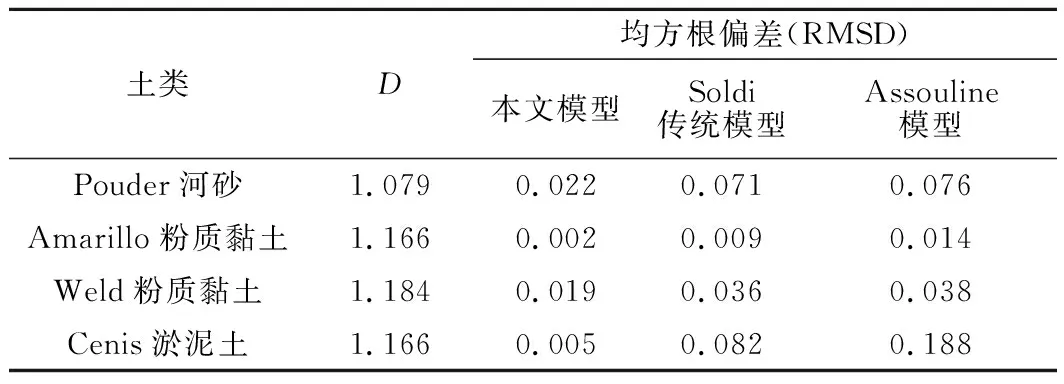
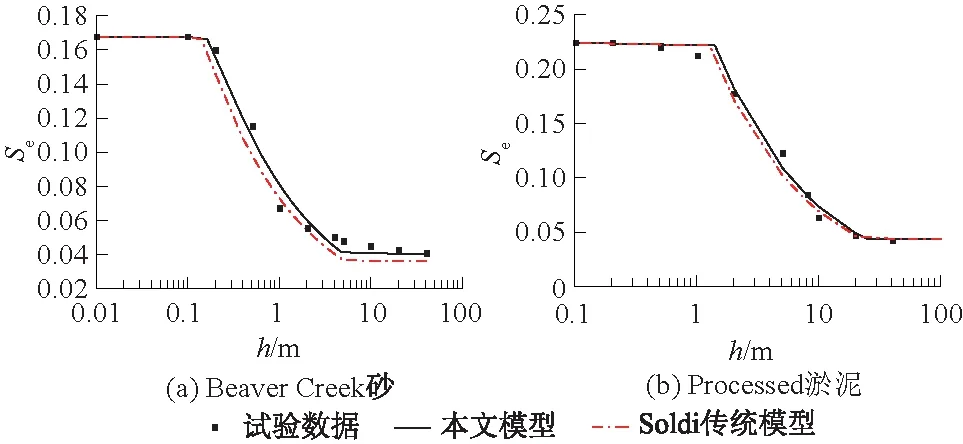
假设土体孔隙可以用一簇服从分形定律且半径在最小毛细管半径rmin和最大毛细管半径rmax之间的毛细管代替,在土体中取一个具有代表性的圆柱体单元(REV),REV的半径为R0,长度为L,如图1所示。假设每根毛细管中的水都处于连续状态,即可流动状态。一般认为,当土中水运动时(一般分为脱湿过程和吸湿过程),存在一个临界半径R(R为毛细管恰好饱和状态时的临界孔隙半径),使得R为控制着毛细管饱和状态和非饱和状态的临界半径,即毛细管半径r=R时恰好为饱和状态,其水头高度恰好为L,则当毛细管半径为rmin≤r≤R时,毛细管为饱和状态;当R 图1 毛细管系统孔隙水分布简化模型Fig.1 Simplified model of pore water distribution in capillary system 基于上述假设,半径为r的单根毛细管体积Vp(r)为 Vp(r)=πr2L。 (1) 饱和状态下单根毛细管的含水体积Vpw1(r)为 Vpw1(r)=Vp(r)=πr2L。 (2) 非饱和状态下单根毛细管的含水体积Vpw2(r)为 Vpw2(r)=πr2h。 (3) 式中:下标p表示单根毛细管;下标w代表水相;h为水头高度。 由杨-拉普拉斯方程,毛细管的水头高度h与其半径r的关系可表示为 (4) 由式(4)得临界半径R为 (5) 式中:Ts为水表面张力;θ为接触角;ρw为水的密度;g为重力加速度。 将式(4)代入式(3)得非饱和状态下单根毛细管的含水体积为 (6) 有学者提出了土体孔隙累积尺寸分布近似服从以下分形定律[18-19],其表达式为 (7) 式中:N(r)表示半径小于r的毛细管总数;D(1 将式(7)对r微分,得到毛细管半径从r到r+dr的毛细管数量为 (8) 其中“-”号代表毛细管的累积数量随着孔径的增大而减少。 毛细管系统的饱和度Se可由饱和度的定义求得 (9) 结合式(3)—式(8)并代入式(9)可得饱和度Se与水头高度h之间的关系式,即土水特征曲线模型为 (10) 其中: 式中hmax、hmin分别表示最大和最小水头高度。 假定水流为层流,则单位时间内单根管的体积流量Qp(r)[20-21]为 (11) 式中μ为水的黏度。 则在饱和流的情况下,单位时间内单元体REV的流量可表示为 (12) 饱和流情况下,由达西定律[22],单位时间内通过单元体REV水流的体积流量可表示为 (13) 式中Ks是饱和渗透系数。 由式(12)、式(13)可得 (14) 另一方面,在非饱和流的情况下,单位时间内通过单元体REV水流的体积流量可表示为 (15) 在非饱和流的情况下,由Buckigham-Darcy定律[23],单位时间内通过单元体REV水流的体积流量可表示为 (16) 式中:kr表示相对渗透系数,它是水头高度h的函数,kr的取值范围在0和1之间。 结合式(14)—式(16)可得 (17) 结合式(4)、式(10)、式(17)得 (18) Yu和Li[24]提出对于土壤而言,rmin/rmax≪10-2。因此,本文假设rmax≫rmin,所以,rmax/rmin趋近于无穷大。另一方面,由于1 (19) 另一方面,(rmax/rmin)2-D约为0,由文献[16]可知,Se=(R/rmax)2-D。将其代入式(19)可得 (20) 将式(20)化简得 (21) 式(21)为非饱和土的饱和度与相对渗透系数模型,其中等式右侧第一项为饱和孔隙的相对渗透系数,第二项为非饱和孔隙的相对渗透系数。式(21)中只含有一个参数,即分形维数D,它决定孔隙体积分布函数,具有明确的几何意义。值得注意的是,当土体处于干燥状态的时候,Se为0,此时kr=0;当土体为饱和状态的时候,Se为1,此时kr=1,与实际相符,这也在一定程度上证明了本文提出的相对渗透系数预测模型的合理性。 本部分用不同土类的试验数据验证提出模型的合理性与可行性。对于每种土,通过均方根偏差(RMSD)评测预测数据与试验数据的误差,如式(1)所示。均方根偏差越小,则说明试验数据与预测数据的误差越小;反之,若均方根偏差越大,则说明试验数据与预测数据的误差越大。 (22) 采用Pouder河砂、Amarillo粉质黏土、Weld粉质黏土和Cenis淤泥土的相对渗透系数共4组试验数据[25]对本文提出的相对渗透系数模型与Assouline模型[7]、Soldi传统模型[17]进行对比,如图2所示。分形维数D通过最小二乘法拟合试验数据得到。将不同土类的拟合参数(D)及本文模型与Soldi传统模型和Assouline模型的均方根偏差(RMSD)列于表1。 图2 不同土类的相对渗透系数预测数据与实测数据对比Fig.2 Comparison between predicted and measured relative permeability coefficient of different soil types 由表1可知,拟合参数1 表1 不同土类的分形维数D及本文模型与Soldi传统模型、Assouline模型的均方根偏差Table 1 Fractal dimension (D) of different soil types and RMSD of the proposed model from Soldi traditional model and Assouline model 采用Beaver Creek砂和Processed淤泥2组非饱和土脱水过程的土水特征曲线试验数据[26]对本文提出的土水特征曲线模型进行验证,并与Soldi传统模型[17]对比,如图3所示。模型参数通过最小二乘法拟合试验曲线得到,将通过拟合2种土类试验数据得到的参数D、hmin、hmax及本文模型与Soldi传统模型的均方根偏差(RMSD)列于表2。 图3 水土特征曲线预测数据与试验数据对比Fig.3 Comparison of predicted and experimental data of soil and water characteristic curve 由表2可知,1 表2 不同土类的D、hmin、hmax及本文模型与Soldi传统模型的均方根偏差(RMSD)Table 2 Fractal dimension D, hmin, and hmax of different soil types as well as RMSD between the proposed model and Soldi traditional model 本文在可用毛细管系统近似代替土孔隙的假设上,基于杨-拉普拉斯方程和分形理论,得到以下结论: (1)对传统的毛细管含水量模型做出了改进,使其更接近孔隙水分布的真实状态。 (2)提出了土水特征曲线概念模型,模型含有3个几何参数(D、hmin、hmax)。经数据分析,相对于传统毛细管系统含水量模型,改进后的模型的土水特征曲线与实际情况更加接近。 (3)提出了非饱和土相对渗透系数概念模型。该模型只含有一个几何参数D,它决定孔隙体积分布函数。通过用4组试验数据对提出的相对渗透系数概念模型进行验证,用均方根偏差(RMSD)评测试验数据与预测数据之间的误差,结果表明4组数据的均方根偏差(RMSD)均<0.025,说明该模型具有预测非饱和土相对渗透系数的实际意义。
3 土水特征曲线模型
4 相对渗透系数曲线模型
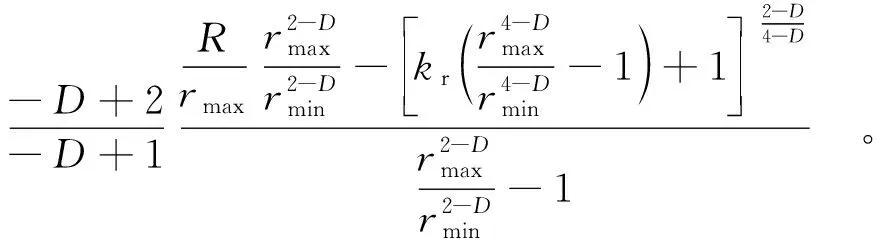
5 试验数据验证

5.1 饱和度-相对渗透系数曲线
5.2 土水特征曲线(SWCC)

6 结 论

